IMU辅助的室内单星定位方法

尚俊娜，刘 参，施浒立，程 涛，岳克强

（1.杭州电子科技大学通信工程学院，杭州 310018；2.中国科学院国家天文台，北京 100012；3.杭州电子科技大学电子信息学院，杭州 310018）

IMU辅助的室内单星定位方法

尚俊娜1，刘 参1，施浒立2，程 涛1，岳克强3

（1.杭州电子科技大学通信工程学院，杭州 310018；2.中国科学院国家天文台，北京 100012；3.杭州电子科技大学电子信息学院，杭州 310018）

惯性导航系统（INS）是以惯性器件测量位置参数的定位系统，但随着时间的累积，系统的定位精度逐步变差，产生累积误差现象。基于无线传感器网络（WSN）的定位技术通常需要3个锚节点进行定位，但在室内复杂环境中，系统会处于锚节点欠定状态，此时需要辅助定位方法解决室内欠星定位问题。针对上述定位系统的不足，提出了一种基于IMU辅助和场景分析的多信息融合室内单星定位方法，该方法可通过场景分析的约束条件逐步消除IMU在室内环境下的累积误差效应，并通过单星定位技术进一步优化定位目标的位置信息。经过地下车库实验验证，本方法平均定位精度是0.75 m，定位误差有97.5%的概率在2 m以内,能满足室内亚米级高精度导航定位的要求。

惯性导航系统；累积误差；场景分析；室内定位；航位推算

导航与定位服务事关国家发展、经济兴起、民众安全，随着智能手机和移动互联网的普及，人们对室内导航定位应用的需求以及高精度的要求也在不断提高。由于室内空间分割多，建筑元素多，环境条件复杂多变，使得定位系统的定位精度较低，故此人们对高精度的室内定位的需求越来越高，众多学者和科研机构在室内定位方面开展大量的研究。张宏刚等提出了一种室内三边定位算法[1]，Hashim等提出了一种基于RSS的Trilateration室内定位技术[2]，然而这种在较大室内环境中设置信号锚节点，采用三球或四球交会原理定位算法，通常需要较多的信号锚节点，会造成系统硬件开支过高、成本投入过大。孙聃石等提出了基于zigbee技术的商场定位系统[3]，朱海等提出了基于CSI的WiFi室内环境感知技术[4]，这些采用室内已有的WiFi、Zigbee、蓝牙等无线信号强度(RSS)特征量进行室内定位导航的系统，由于室内环境下RSS值随距离衰减曲线波动严重，无法得到准确的室内信号传播模型，通常系统的定位精度低、稳定性较差，无法得到普适应用。Zhang Huiqing等提出基于MEMS惯性器件和智能手机的室内导航算法[5]，这种采用惯性器件进行室内位置推算的系统，通常采用的惯性器件测量精度较差，且存在误差漂移和累积误差现象，难以保证定位准确性。故此，低成本、高精度的室内定位系统，受到越来越多人的青睐。目前研究较多的是基于惯导辅助的组合导航定位系统，如阳洪等提出的基于MEMS/IMU/GNSS的室内外无缝定位系统[6]，以及周先赞等提出的基于超声波/INS信息融合的室内定位方法[7]。

在基于惯导辅助定位研究中，一方面，惯性测量单元存在较大测量误差，且在位置推算过程中存在累积误差现象，另一方面，定位需要依靠大量定位锚节点，至少要接收到三个以上锚节点信息才能实现定位。而室内环境空间分割较多，信号阻挡严重，很多区域难以保证接收到三个以上锚节点信息，系统会处于锚节点欠定状态，此时需要寻找有效的欠星定位方法来解决上述定位问题。基于此，本文提出一种基于IMU辅助和室内地图匹配的多信息融合室内单星定位方法，该方法可通过室内场景分析的约束条件逐步消除IMU在室内环境下的累积误差效应，并通过单星定位技术进一步优化定位目标的位置信息，经过实验验证，在复杂地下车库等室内欠星环境中可实现亚米级定位精度的需求。

1 IMU惯性导航定位系统误差分析

惯性导航系统的基础是对加速度的测量[8-10]，通过积分的方法获得载体速度和位移，所用的数学原理是牛顿运动定律。其中测量装置由陀螺仪和加速度计组成，通常包括3个自由度陀螺仪用来测量载体运动不同方向的转动角速度，3个加速度计用来测量载体平移运动在不同方向上的加速度。当获得载体运动的方向和运动速度以后，采用经典的航位推算(DR)[11]算法可进行导航定位。

惯性导航系统的精度通常取决于陀螺仪的测量精度，故此陀螺仪是惯导系统的“心脏”，但在实际应用中，单纯依靠惯性器件进行导航定位时会存在累计误差效应使得定位精度越来越差。惯性导航系统的定位误差主要是由陀螺仪漂移率、加速度计零偏移以及定位初始位置误差引起的[12]，例如：陀螺仪存在固有随机漂移率，使航位角测量精度随时间逐渐变差。表1是目前主流IMU器件的随机漂移率。从表1中可知：不同的IMU器件的随机漂移率是不一样，但随着时间的增加这种漂移是无法预知的；加速度计易受室内地磁环境影响，造成加速度测量值不稳定，使惯导系统的定位精度较低。在连续使用惯性器件进行导航定位时，上述各种误差会产生累计误差效应，因此无法进行高精度导航定位。

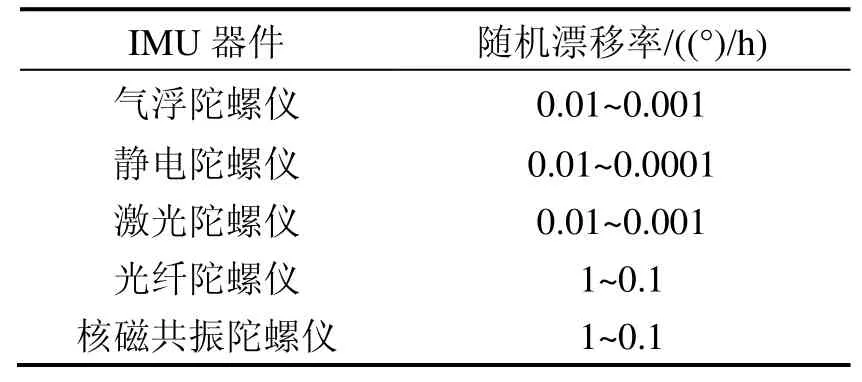
表1 IMU惯性器件的随机漂移性能Tab.1 Random drift performance of the IMU device

为定量分析惯性器件测量误差分布情况，本文采用 JY-901九轴陀螺仪在中科院国家天文台地下车库进行了测试。JY-901系列模块集成高精度的陀螺仪、加速度计、地磁场传感器，该模块的量程、分辨率和稳定性等性能参数如表2所示，所选测试路径如图1带箭头实线所示。

表2 JY-901系列模块性能参数Tab.2 J Y-901 module performance parameters

测试时沿图 1中红色箭头所示路径，将 JY-901陀螺仪模块固定在载体上，以1 m/s匀速沿图中红色箭头方向运动，陀螺仪模块数据通过串口输出到 PC端，所测数据曲线如图2所示。

由图2可以看出，陀螺仪测试的时候，图 2(a)中三轴加速度的y轴加速度随时间逐步漂移，图2(b)中三轴角速度在载体运动过程中均有较大波动，图2(c)中三轴角度中的航向角也有很大波动。综合分析可知，由于测试用JY-901陀螺仪模块集成了地磁传感器，可有效抑制角度测量的误差漂移，但地磁传感器容易受室内电磁等复杂环境的干扰，使得航偏角的波动较为明显。

针对上述测试数据，单独用陀螺仪模块进行定位，以1 m/s作为载体当前运动速度，陀螺仪输出Z轴角度作为载体当前的航向角，利用航位推算算法可不断更新当前位置坐标，得到载体运动轨迹，其中，定位效果如图1曲线所示。

图1中，蓝色曲线为利用陀螺仪模块利用航位推算得到的运动轨迹，红色箭头为真实运动路线。经过对比可以看出，单纯依靠惯性器件进行航位推算的定位系统由于每次定位推算都要依靠上一次的先验数据，导致定位点存在误差累积现象，使得系统的定位精度随着时间累积逐渐变差。故此单独采用IMU模块进行航位推算的定位系统会造成误差累计现象，使得系统定位误差过大，因此需要结合其他定位方法进一步消除累积误差效应。

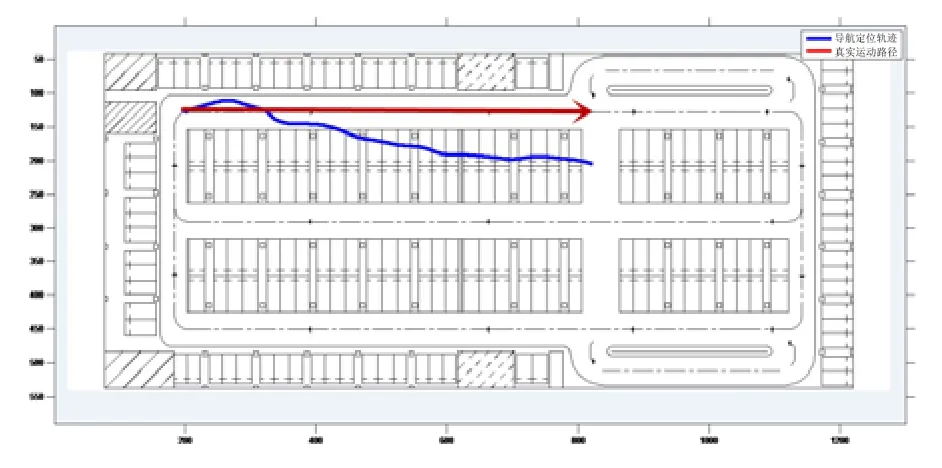
图1 测试路径及惯性器件导航定位轨迹Fig.1 Test path and inertial device navigation positioning trajectory

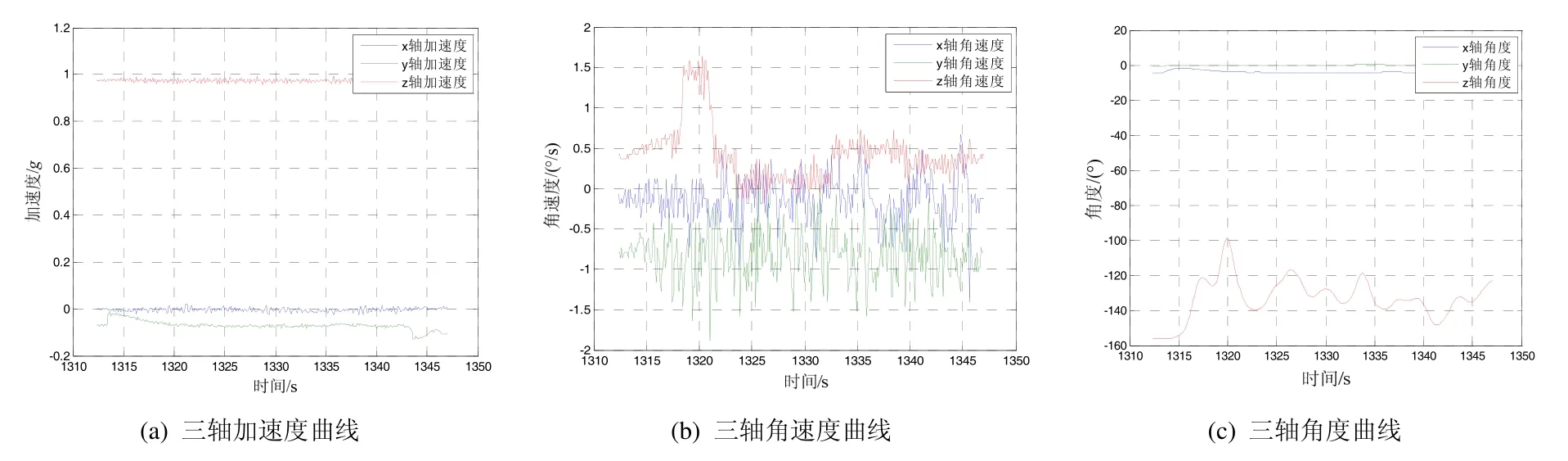
图2 JY-901陀螺仪模块测试曲线Fig.2 JY-901 gyroscope module test curve

2 基于IMU辅助的室内单星定位方法

2.1 IMU辅助单星定位系统方案设计

针对 IMU 定位系统的累计误差现象[13-16]以及复杂室内环境中定位系统处于锚节点欠定状态，本文提出一种基于 IMU辅助和室内地图匹配的多信息融合室内单星定位方法。该方法不同于常规的三边定位原理，而是充分利用先验信息、角度信息、伪距信息和室内场景地图等信息，通过多信息的融合技术实现欠星条件下的室内定位，该欠星定位系统可通过场景分析的约束条件逐步消除 IMU在室内环境下的累积误差效应，并通过单星定位技术进一步优化定位目标的位置信息，其室内定位原理如图3所示。

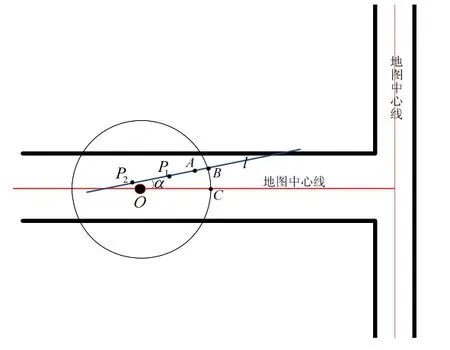
图3 室内单星定位原理图Fig.3 Indoor single star positioning schematic

针对上述A、B、C三个定位坐标点，可设计一种加权融合算法，分别考虑每个位置点的整体误差分布，按照一定规则给每个局部估计值制定加权因子，让误差较小的坐标点具有更高的权重，使最终输出的定位目标的位置可以兼顾每个局部位置的估计值，通过综合考虑所有的局部估计量，进一步优化定位目标的位置，提升系统的定位性能。

利用加权融合算法对图3中A、B、C三点进行融合作为最终定位点X。假设上述所求A、B、C三个位置点的误差模型互不相关，通过设计一种加权融合器对各子系统数据进行加权融合处理，在最小均方根误差准则下，建立加权融合方程：

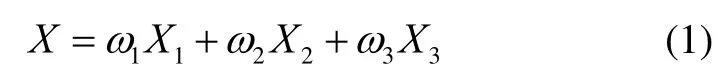
2.2 加权融合算法权值选取

假设定位目标的真实坐标为Xtrue，则有：

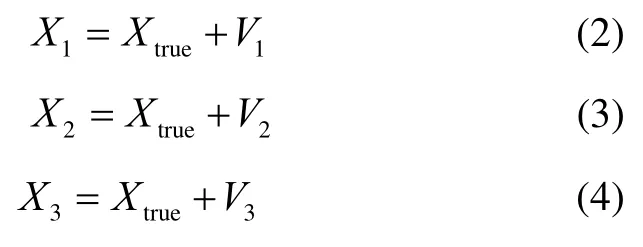
式中：V1为航位推算定位观测噪声，其方差为伪距圆与前进方向定位误差噪声，其方差为为道路中心线匹配误差噪声，其方差为

通过式(1)定位数据加权融合，融合后的误差为：

融合后误差方差为：

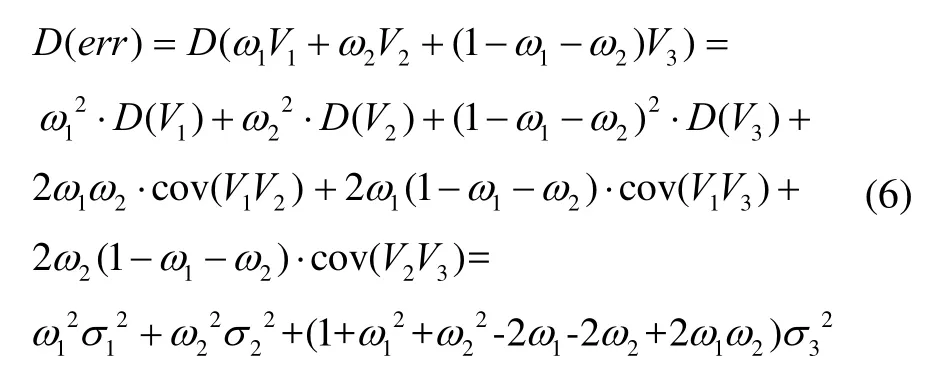
式中：D( )表示方差；cov( )表示协方差。

为了使得加权融合以后系统的定位误差方差最小，对式(6)分别对加权因子求偏导数，使得各自的偏导数为0。经过整理以后可得权重系数为

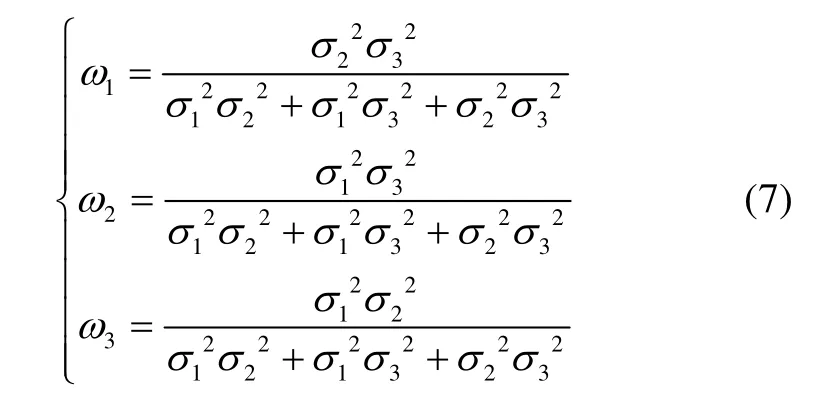
由式(7)可以看出，每个局部估计值的加权值都随着本身误差的增大而减小，即该估计值的误差越大，权值所占比重越小。因此，通过对多信息量的加权融合处理后，单星定位系统的精度既充分利用了各子系统的估计值又有效抑制了局部大噪声对整体精度的影响，故理论上证明了该加权融合方法可以进一步提升系统的定位性能，可在室内欠星环境中提高系统的定位精度。

2.3 系统误差分析

系统定位结果用y表示，该结果是关于ρ,v,α,k测量变量的函数，ρ是测量伪距，v是载体的运动速度，α是载体运动的航向角，k是地图中心线方程，则y可表示为

函数y的增量可以用函数y的全微分表示：

若分别已知每个测量值的典型测量误差，当这些误差值较小时，可用这些测量误差近似代替式(9)的微分量[17]，可得到函数的近似系统误差Δy：

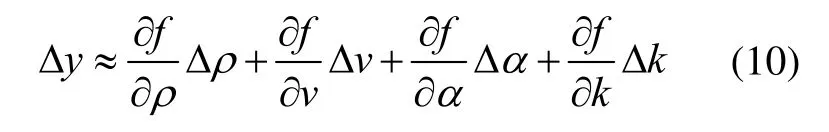
本文通过单星系统实现伪距的测量，其中单个锚节点发送线性调频信号(CSS)，采用基于信号到达时间(TOA)的方法进行伪距测量[18]。为了消除系统时钟不同步带来的伪距误差，本文采用SDS-TWR技术进一步提升系统的测距性能[19]，通过对TOA的准确估计，可以得到定位目标与锚节点之间的伪距。为了消除环境和噪声对伪距的影响，本文对锚节点的伪距误差进行分析。为得到单点测距精度，在国家天文台地下车库进行了单点测距实验，固定锚节点，沿一个方向移动移动节点，每隔0.5 m进行一测测试，每次采取30个伪距测量值，进行均值处理作为当前点伪距值，伪距误差以及误差累积分布曲线如图4所示。从图4中可以得出在车库中锚节点的测距误差整体都在 1.1 m以下，误差均值E=0.6731 m，标准差σ=0.4142 m。通过先验信息对伪距进行误差校正，消除均值误差，进一步提升单星测距性能。

图4 锚节点测距误差以及误差累积分布曲线Fig.4 Anchor node ranging error and error cumulative distribution curve

本文提出的加权融合算法在三个加权点处的误差分析如下所示：

a).航位推算点A的误差ΔAε

航位推算理论偏差如图5所示。

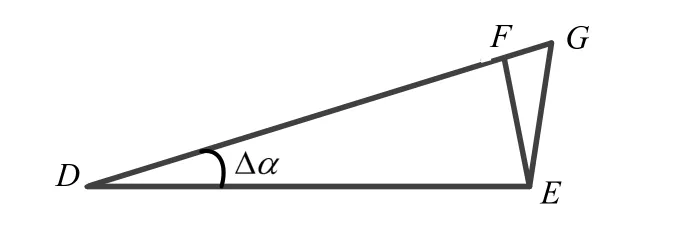
图5 航位推算理论偏差示意图Fig.5 Estimation of theoretical deviation of the dead reckoning

图5中，D为初始位置点，E是下一时刻的真实位置，表示该时间段内载体运动的距离，Δα是由于航向角误差造成载体角度的偏差，表示由于速度的误差造成载体运动距离的误差，G表示通过航位推算算法得到的载体位置，故此航位推算理论偏差为

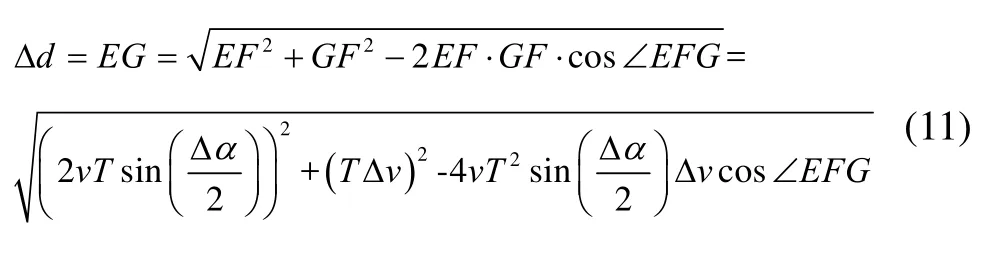
从图3可知航位推算点A的坐标由几何关系得知：

式中：v是定位目标当前运动的速度，T为磁罗盘输出两连续数据的时间间隔，由式(12)可解得A点坐标

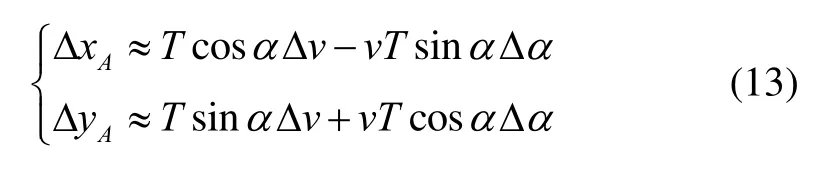
故此航位推算点A的误差ΔAε为

当Δθ比较小时，可用EF≈vTΔα带入理论误差公式(11)并且忽略最后一项，即得公式(14)，故此可认为这种近似是合理有效的。

由式(14)可知，航位推算点A的误差与载体运动速度和航向角的精度呈正相关特性，当速度和航向角精度固定的时候，运动速度越快，误差越大。

b).伪距圆定位点B的误差ΔBε

从图3可知，伪距圆与前进方向定位点B的坐标由几何关系知，直线l的方程为

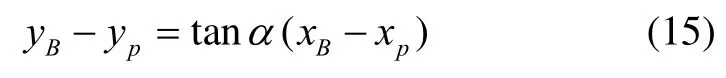
联立直线l和圆的方程可得：

式中：ρ为测得的定位目标到锚节点之间的伪距，求解式(15)可得B点坐标

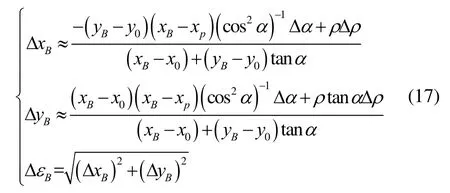
由式(17)可知，定位点B的误差ΔBε不仅与载体运动的航向角测量值以及精度有关，还与伪距的测量值以及精度有关，同时还与定位点B有关，并且该误差具有复杂的函数关系。当伪距误差变大时，由于航位角α的影响，使得x坐标误差ΔxB和y坐标误差ΔyB不同比例的增加，故此在实际应用中，可以通过一定的约束条件对误差函数进一步简化处理。

c).道路中心线匹配点C的误差ΔCε

从图3可知，道路中心线匹配点C的坐标由几何关系知，地图中心线方程为y=k，则有：

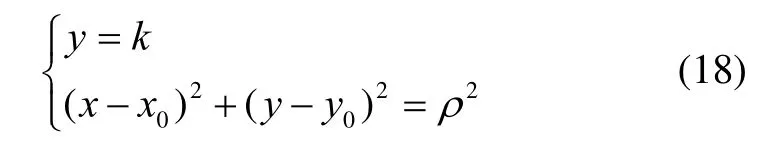
求解式(18)，可得C点坐标

与上述b)小节分析思路相同，可得道路中心线匹配点C的坐标xC和yC的误差以及定位点C的误差ΔCε。

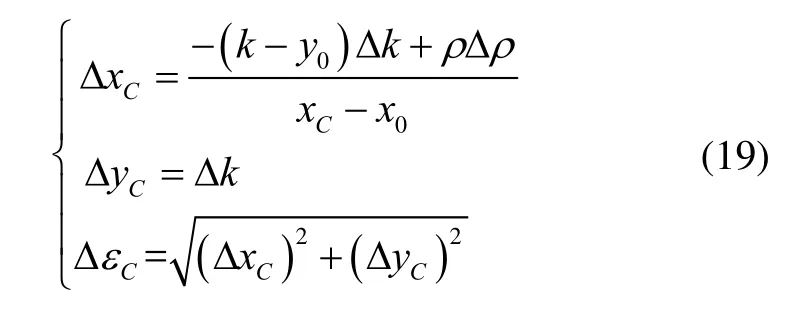
由式(19)可知，定位点C的误差ΔCε不仅伪距的测量值以及精度有关，还与地图中心线方程的参数以及精度有关，同时还是定位点B坐标为变量的函数，当伪距误差变大时，x坐标误差ΔxC增加，使得定位性能变差。

3 单星定位方法实验验证

为了验证本文提出 IMU辅助室内单星定位方法的可行性，在中科院国家天文台地下车库用小推车进行了实验验证。测试采用JY-901九轴陀螺仪模块测量航向角，装置在小车轮子上的速度传感器测量小推车速度信息，其中，地下车库的规模为2120× 50m ，测试用小推车如图 6(a)及测试场景如图 6(b)所示，单个锚节点为位置、车位与柱子分布情况如图 6(c)所示。试验参数典型值为：伪距误差的典型值本文采用的 JY-901系列模块的运动速度误差典型值航向角误差典型值表示系统运行的持续时间。由于试验所示地图的精度在1 m左右，故此地图中心线方程误差的典型值Δk=1m。加权融合算法各个权系数选择如公式(7)所示，其中，航位推算定位观测噪声的选取如式(14)，伪距圆与前进方向定位误差噪声的选取如式(17)，道路中心线匹配误差噪声的选取如式(19)。

本实验最终定位结果实如图6(c)所示，其中，红色“o”为锚节点位置，框1处为小推车走S形轨迹，框2处为小推车进出车位轨迹，框3处为小推车在拐角处转弯以后形成的轨迹。

图6 实验用车、测试场景和实验测试轨迹图Fig.6 Experimental vehicle diagram and test scenarios and test track diagram

从图6(c)可看出：当小推车就行S形轨迹运动的时候，定位效果明显呈现S形轨迹，如框1所示；在框2中，小推车进出停车位的时候，定位系统可以检测到车子进入了车库，同时还可以检测出来车子离开了车库，其中定位的停车位与实际小推车进入的停车位一致；框3中，当车子在车库边界处转弯的时候，系统可以实时检测到车子的动态，并且显示出来车子转弯的轨迹。

本文对图6(c)中框1所示的S形轨迹的定位性能就行分析，定位性能评价函数用均方根误差(RMSE)表示，其中表示是x方向和y方向的定位误差分量。图7统计了本文采用算法与传统航位推算(DR)算法在测试车库中 S形轨迹的定位精度累积分布曲线图，不同定位精度的概率分布如表3所示。

从图7和表3可知，本文采用算法在1 m和3 m内的定位精度置信概率分别为 71.5%和 98.4%，高出传统DR算法65.8%和48.2%，并且本文采用算法的平均定位精度是0.75 m，定位误差有97.5%的概率在2 m以内，而传统DR算法的定位误差高达9 m。故此，该欠星定位方法的平均定位精度优于 1 m，可实现亚米级精度的定位需求。

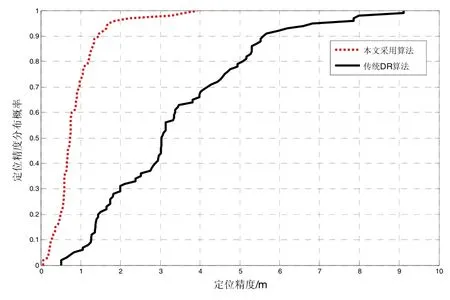
图7 不同算法的定位精度累积分布曲线Fig.7 The cumulative distribution of positioning accuracy of different algorithms

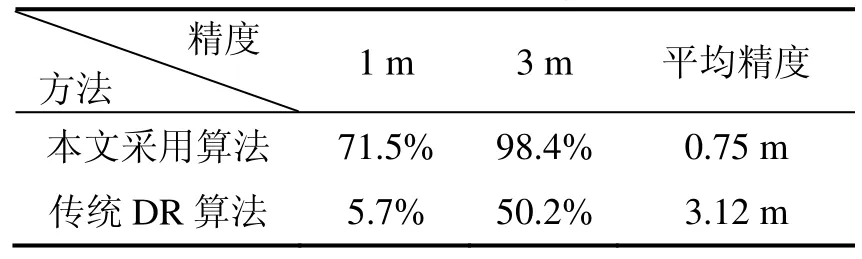
表3 不同算法定位精度的概率分布值Tab.3 Probability distribution of positioning accuracy for different algorithms

4 结 论

本文针对室内环境下分割阻挡多，系统会处于欠定状态以及惯性器件受环境因素干扰严重等问题提出了一种基于 IMU辅助和室内地图匹配的多信息融合室内单星定位方法。该方法充分利用当前地理信息、先验数据信息、伪距信息，实现多信息融合，并依据误差方差最小化准则给出了各信息数据的加权融合方案。由于充分利用了各子系统信息又有效抑制了各子系统噪声影响，可进一步提升系统的定位性能。在实际复杂的室内车库环境中进行实验验证，本文采用算法的平均定位精度是0.75 m，定位误差有97.5%的概率在2 m以内，而传统DR算法的定位误差高达9 m。故此，该欠星定位方法的平均定位精度优于1 m，可实现亚米级精度的定位需求。

（Reference）：

[1]张宏刚, 黄华.基于RSSI路径损耗因子动态修正的三边质心定位算法[J].传感技术学报, 2016, 29(11):1731-1736.Zhang H G, Huang H.Dynamic correction algorithm for trilateral centroid localization based on RSSI path loss factor[J].Chinese Journal of Sensors & Actuators, 2016,29(11): 1731-1736.

[2]Hashim M S M, Aman M A S S, Wai L K, et al.Indoor localization approach based on received signal strength(RSS) and trilateration technique[C]//International Conference on Mathematics, Engineering and Industrial Applications.2016: 030028.

[3]孙聃石, 杨力, 赵海山, 等.基于ZigBee技术的商场定位系统建立[J].测绘工程, 2017, 26(2): 48-51.Sun D S, Yang L, Zhao H S, et al.A shopping mall positioning system based on ZigBee technology[J].Engineering of Surveying and Mapping, 2017, 26(2): 48-51.

[4]朱海, 肖甫, 孙力娟, 等.基于信道状态信息的 WiFi环境感知技术[J].南京邮电大学学报(自然科学版),2016, 36(1): 94-103.Zhu H, Xiao P, Sun L J, et al.CSI-based WiFi environment sensing[J].Journal of Nanjing University of Posts and Telecommunications (Natural Science Edition),2016, 36(1): 94-103.

[5]Zhang H Q, Dai R Y, Xu X M.Study on indoor positioning and navigation algorithms based on the MEMS inertial devices and smartphone[C]//Chinese Control and Decision Conference.2016: 1787-1792.

[6]阳洪, 刘勇, 刘程, 等.基于MEMSIMU/GNSS/磁力计/气压高度计的单兵组合惯导系统[C]//中国惯性技术学会学术年会, 2015.

[7]Zhou X Z, Xiong J, Guo H, et al.The indoor positioning method based on ultrasonic/INS information fusion[J].Piezoelectrics & Acoustooptics, 2016, 38(2): 316-319.

[8]Skog I, Nilsson J O, Händel P.Evaluation of zero-velocity detectors for foot-mounted inertial navigation systems[C]//International Conference on Indoor Positioning and Indoor Navigation.2010: 1-6.

[9]Groves P D.Navigation using inertial sensors (Tutorial)[J].IEEE Aerospace & Electronic Systems Magazine,2015, 30(2): 42-69.

[10]刘春燕.基于多源信息融合的行人航位推算室内定位方法[J].中国惯性技术学报, 2016, 24(2): 208-214.Liu C Y.Indoor localization method based on pede strian dead reckoning aided by multi-source fusion[J].Journal of Chinese Inertial Technology, 2016, 24(2): 208-214.

[11]Hostettler R, Sarkka S.IMU and magnetometer modeling for smartphone-based PDR[C]//International Conference on Indoor Positioning and Indoor Navigation.2016: 1-8.

[12]吴俊伟, 曾启明, 聂莉娟.惯性导航系统的误差估计[J].中国惯性技术学报, 2002, 10(6): 1-5.Wu J W, Zeng Q M, Nie L J.Estimation of the INS’s errors[J].Journal of Chinese Inertial Technology, 2002,10(6): 1-5.

[13]Zhang R, Hoflinger F, Reindl L.Inertial sensor based indoor localization and monitoring system for emergency responders[J].IEEE Sensors Journal, 2013, 13(2): 838-848.

[14]周绍磊, 吴修振, 刘刚, 等.一种单目视觉ORB-SLAM/INS组合导航方法[J].中国惯性技术学报,2016, 24(5): 633-637.Zhou S L, Wu X Z, Liu G, et al.Integrated navigation method of monocular ORB-SLAM/INS[J].Journal of Chinese Inertial Technology, 2016, 24(5): 633-637.

[15]Wang Z L, Zhao H Y, Qiu S, et al.Stance-phase detection for ZUPT-aided foot-mounted pedestrian navigation system[J].IEEE/ASME Transactions on Mechatronics,2015, 20(6): 3170-3181.

[16]张瑜, 陈丹丹, 吕明.信标欠定时的井下人员定位算法[J].传感器与微系统, 2014, 33(3): 154-156.Zhang Y, Chen D D, Lyu M.Localization algori- thm for person under coal mine in beacon nodes underdetermined circumstances[J].Transducer and Microsystem Technologies, 2014, 33(3): 154-156.

[17]谭雁英, 周旗, 张波, 等.小型无人机航位推算定位算法研究与误差分析[J].火力与指挥控制, 2007, 32(5):8-11.Tan Y Y, Zhou Q, Zhang B, et al.Dead reckoning method and error analysis for small UAVs[J].Fire Control and Command Control, 2007, 32(5): 8-11.

[18]Li Y C, Chong J W.High-resolution range estimation technique using shift invariant TOA estimation algorithm for indoor localization of chirp spread spectrum system[C]//IEEE International Conference on Network Infrastructure and Digital Content.2012: 567-572.

[19]Kwak M, Chong J.A new double two-way ranging algorithm for ranging system[C]//2nd IEEE International Conference on Network Infrastructure and Digital Content.2010: 470-473.

Indoor single-star positioning method based on IMU assisting

SHANG Jun-na1, LIU Can1, SHI Hu-li2, CHENG Tao1, YUE Ke-qiang3
(1.College of Telecommunication Engineering, Hangzhou Dianzi University, Hangzhou 310018, China;2.National Astronomical Observatories of Chinese Academy of Science, Beijing 100012, China;3.College of Electronic Information, Hangzhou Dianzi University, Hangzhou 310018, China)

The inertial navigation system (INS) is a positioning system that measures the position parameters by the inertial device.However, with the accumulation of time, the positioning accuracy of the system is gradually deteriorated, resulting in cumulative error.Based on the fact that the wireless sensor network (WSN)positioning technology usually requires three anchor nodes to locate, but in the indoor environment, the system will be in the anchor node underdetermined circumstances, assisting the positioning method is needed to solve the problem of indoor positioning.Focusing on the shortcomings of the above-mentioned positioning system, a multi-information fusion indoor single-star positioning method based on IMU assistant and scene analysis is proposed, which can gradually eliminate the cumulative error effect of IMU in the indoor environment through the constraint of scene analysis, and further optimize the position of positioning target by single-star positioning technique.The underground garage experiment verify that the average positioning accuracy of this method is better than 0.75 m, and the positioning error of 97.5% is within 2 m, which can meet the indoor sub-level high-precision positioning requirement.

inertial navigation system; accumulative error; scenario analysis; indoor positioning; dead reckoning

TP391

A

1005-6734(2017)05-0636-07

10.13695/j.cnki.12-1222/o3.2017.05.014

2017-05-01 ；

2017-08-23

国家自然科学基金资助项目（11603041）；浙江省自然科学基金青年基金（LQ13F010010）

尚俊娜（1979—），女，博士，副教授，主要研究方向为卫星导航、室内定位。E-mail: shangjn@hdu.edu.cn