基于EGM2008重力场球谐模型的水平重力扰动计算方法

铁俊波，吴美平，蔡劭琨，张开东，练军想

（国防科技大学 机电工程与自动化学院，长沙 410073）

基于EGM2008重力场球谐模型的水平重力扰动计算方法

铁俊波1，吴美平1，蔡劭琨1，张开东1，练军想1

（国防科技大学 机电工程与自动化学院，长沙 410073）

垂线偏差数据对于提高惯性导航精度具有重要意义，阐述了使用重力场球谐模型计算水平重力扰动的方法，使用EGM2008重力场球谐模型计算水平重力扰动，并将其与美国国家地理空间情报局提供的全球2.5′2.5′× 垂线偏差网格数据进行对比，验证了所述水平重力扰动计算方法的正确性。将水平重力扰动计算结果用于航空、车载惯性导航数据离线处理，结果表明EGM2008模型计算的水平重力扰动可用于补偿惯性导航；将水平重力扰动计算结果用于长航时船载惯性导航数据离线处理，结果表明惯性导航精度最大提升1.5 n mile，平均提升0.8 n mile。

惯性导航；重力扰动；重力场球谐模型；垂线偏差补偿

为进一步提高惯性导航精度，补偿水平重力扰动对惯性导航的影响是必须要解决的问题[4-7,15-18]，而获取高精度的水平重力扰动数据就是首先要面对的问题。水平重力扰动数据的测量是困难的，使用天文方法可以静态、单点测量，但效率很低，难以获取区域数据。捷联式重力矢量测量方法有望在未来成为高效的水平重力扰动测量手段，通过直接求差法[2-3]或姿态求差法[19-21]可以获得水平重力扰动数据，但其对水平姿态测量精度要求非常高，为提高重力矢量测量精度需进一步研究姿态误差分离、传感器漂移补偿等问题[3]。目前获取大面积水平重力扰动的可行方法是利用全球重力场球谐模型计算水平重力扰动，近年来国内学者研究了使用重力场模型计算水平重力扰动用于提高惯性导航精度的方法。文献[4-5]以美国国家大地数据测量局（National Geospatial-Intellgence Agency, NGA）提供的垂线偏差网格数据对惯性导航系统进行了补偿，但使用网格数据需要插值及延拓处理。文献[6-7]使用重力场球谐模型直接计算水平重力扰动，但其给出的水平重力扰动计算方法不完整。为此本文阐明了使用球谐模型计算重力扰动的方法，将计算结果与NGA官方提供的垂线偏差网格数据进行比较，并结合航空、车载及船载激光陀螺捷联惯性导航数据对所计算的水平重力扰动数据能否提高惯性导航精度进行了验证。

1 扰动重力位与水平重力扰动

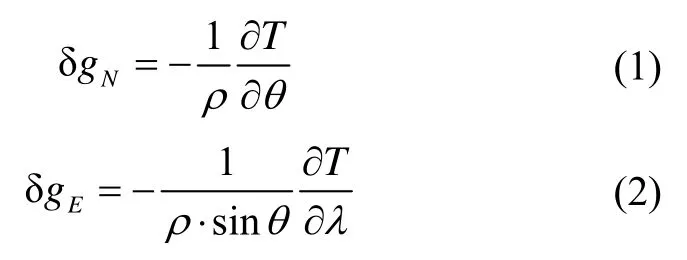
其中：δgN、δgE为北向、东向重力扰动；θ为计算点的地心余纬度，又称为极距（Polar Distance）；λ为计算点经度；ρ为计算点到参考椭球球心的距离。扰动重力位满足拉普拉斯方程，可用球谐函数展开：

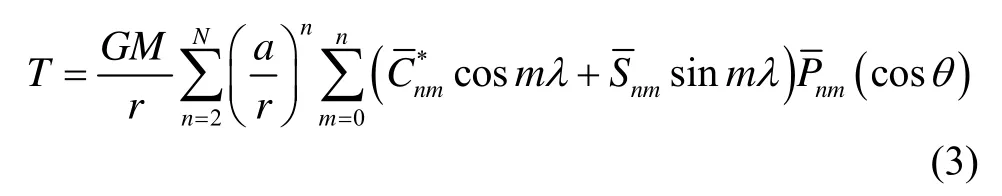
图1 垂线偏差示意图Fig.1 The definition of vertical deflection

由重力扰动位与水平重力扰动关系(1)(2)及重力扰动位的球谐函数表达式(3)，可以得到水平重力扰动计算公式[1,10-12]：

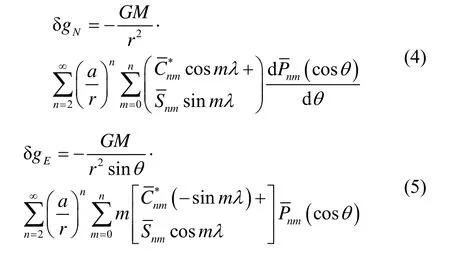
完全正常化勒让德函数通过地推的方式进行求解，需要注意的是，计算以阶n为顺序递推，即n为变量、m为常量，其递推公式如下（根据n与m的取值关系，递推时分为3种情况）[7,9]：

完全正常化勒让德函数递推初值为

由式(4)(5)看到，使用球谐模型计算东向重力扰动仅需要完全正常化勒让德函数，但求解北向重力扰动还需要完全正常化勒让德函数的导数。文献[7]给出的求解完全正常化勒让德函导数的公式是相对于cosθ的导数，而由公式(4)看到，计算北向水平重力扰动的导数应是相对于θ的导数，使用如下递推公式计算[8]：

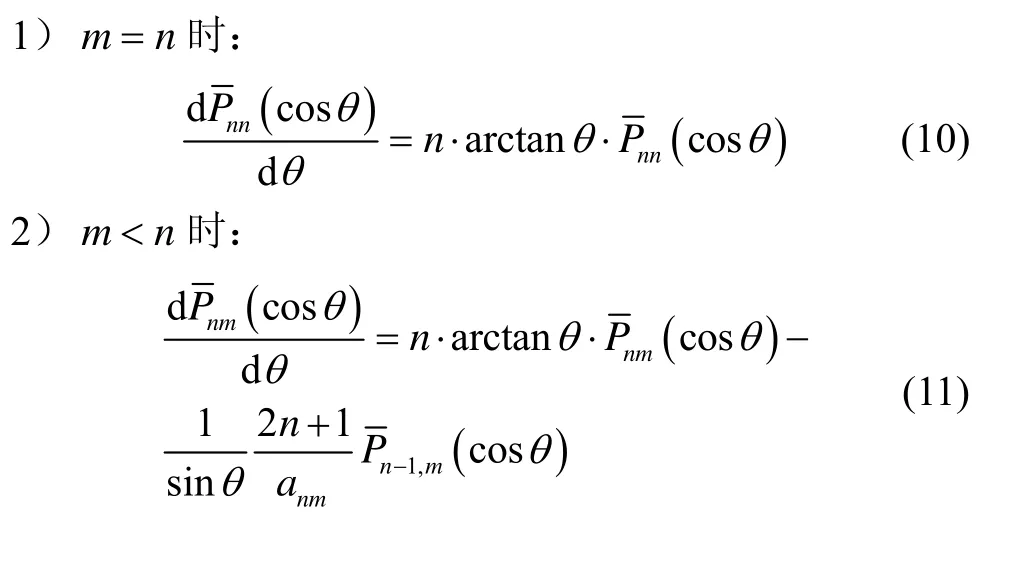
2 扰动重力位球谐函数计算水平重力扰动方法

完全正常化勒让德函数及其导数的计算是使用球谐模型计算水平重力扰动的关键，由公式(6)～(11)可以看到：m=n的完全正常化勒让德函数及其导数可以直接递推计算，将其计算过程称之为“等阶次完全正常化勒让德函数及其导数计算”；而m＜n的完全正常化勒让德函数及其导数的计算有赖于等阶次完全正常化勒让德函数及其导数的计算结果，将此计算过程称之为“非等阶次完全正常化勒让德函数及其导数计算”。水平重力扰动算法流程如图2所示。

图2 球谐模型计算水平重力扰动算法流程图Fig.2 The calculation scheme of vertical deflection based on gravity harmonic model

第一步：参考椭球参数初始化

根据给定的参考椭球的4个基本参数，计算其它参数，4个基本参数包括：长半轴a、椭球的扁率f或2阶带状球谐系数J2、地心引力常数GM及地球自转角速率Ω。这4个基本不仅决定了参考椭球的形状，还确定了与此参考椭球对应的正常重力场。NGA官方提供的球谐系数是在WGS-84椭球模型下计算得到，惯性导航一般也是以WGS-84为参考椭球，当使用其它椭球模型时，NGA提供的球谐系数模型需要进行一定处理，WGS-84椭球坐标系的4个基本参数取值如表1所示。

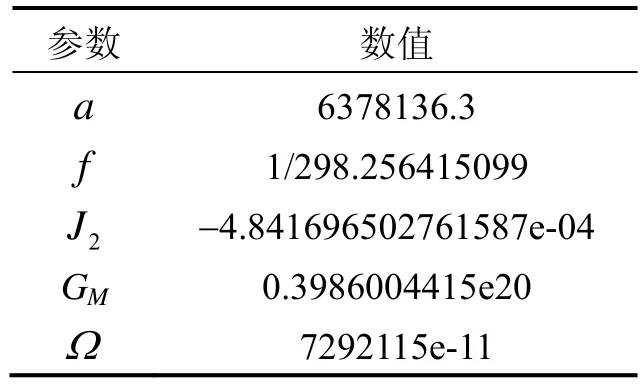
表1 WGS-84椭球模型基本参数Tab.1 Fundamental parameter of WGS-84

第二步：读取球谐模型系数并处理

EGM2008官方网站[10]给出了无潮汐假设（Tide-Free）下EGM2008重力场球谐模型系数文件：系数文件的第1列为阶n；第2列为次m；第3、4列为与完全正常化勒让德函数对应的球谐系数该系数是在WGS-84坐标系下计算得到，当使用的参考椭球非WGS-84时，需要对其进行改正。水平重力扰动是与扰动重力位相关，NGA提供的EGM2008球谐系数是重力位球谐系数而非扰动重力位球谐系数，因此需要将正常重力场从其中扣去后得到所需的扰动重力位球谐系数。令正常重力位球谐系数中与cosmλ相关项为使用如下公式(14)将其从EGM2008球谐系数中扣除，得到扰动重力位的球谐系数

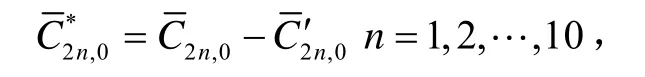
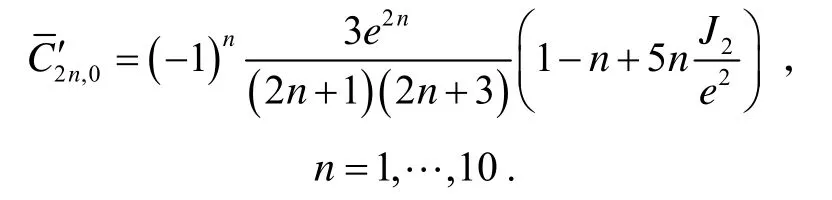
e为椭球的第一离心率，可由扁率f计算得到：

第三步：读取计算点坐标及非勒让德函数项计算

重力场扰动位球谐模型公式中的θ为地心余纬度，当输入计算点坐标为地心纬度时可以直接用π/2减去地心纬度后得到地心余纬度θ。而惯性导航、卫星导航中一般使用大地纬度，因此需要将大地纬度转换为地心纬度。扰动位球谐函数中的项与完全正常化勒让德函数无关，可以单独计算。需要注意的是，在计算时，NGA的官方程序中给项乘以了系数乘以此系数的目的是为了提高完全正常化勒让德函数的数值计算精度[13]。

第四步：等阶次完全正常化勒让德函数及其导数计算

第五步：非等阶次完全正常化缔合勒让德多项式及其导数计算

第六步：水平重力扰动计算将第二步得到的球谐系数，第三步得到的计算点地心余纬度、非勒让德函数项，第四、五步得到的完全正常化勒让德函数及其导数代入公式(4)(5)得到计算点处的水平重力扰动。

3 与NGA提供垂线偏差网格数据比较

将水平重力扰动计算结果与 NGA官方提供的全球垂线偏差网格数据比较，以验证所述算法计算结果的正确性。NGA官方提供了全球分辨率为2.5′2.5′× 的垂线偏差网格数据，需要注意的是，该网格数据是椭球面上的垂线偏差网格数据，将其乘以正常重力γ后即可得到水平重力扰动，正常重力计算公式参见文献[13]，水平重力扰动与垂线偏差关系为

取 NGA 提供的网格数据中范围为 10°N～11°N（大地纬度），110°E～112°E 的网格垂线偏差数据，利用公式(12)(13)将其转换为水平重力扰动。获取其坐标后使用所述方法计算水平重力扰动，两者差异如表 2、图 3～4所示，存在差异的主要原因在于NGA给出的网格数据是该网格区域的平均值，而使用球谐模型计算的水平重力扰动是计算点处的单点值，因此存在微小差别。

表2 水平重力扰动计算结果差异统计Tab.2 Differences between grid datum and computation

图3 水平重力扰动南北向分量差异Fig.3 Differences of north-south component

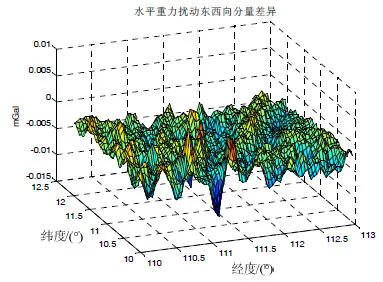
图4 水平重力扰动东西向分量差异图Fig.4 Differences of east-west component

4 实测数据验证

计算水平重力扰动的目的是提高惯性导航精度，使用航空及车载试验数据对所述水平重力扰动计算方法进行验证。车载数据为湖南某地90型激光捷联惯导系统车载试验数据，试验车向西北方向行驶，时间约4 h；航空数据为山东某沿海地区的90型激光捷联惯导系统飞行试验数据，载机沿东西向往返飞行，时间约4 h。根据采样率为2 Hz的差分GPS给出的大地纬度、经度及高度，以所述算法计算载体出发点及运动路径上的水平重力扰动，如图5～6所示。两次试验路径上的水平重力扰动统计信息见表3所示。

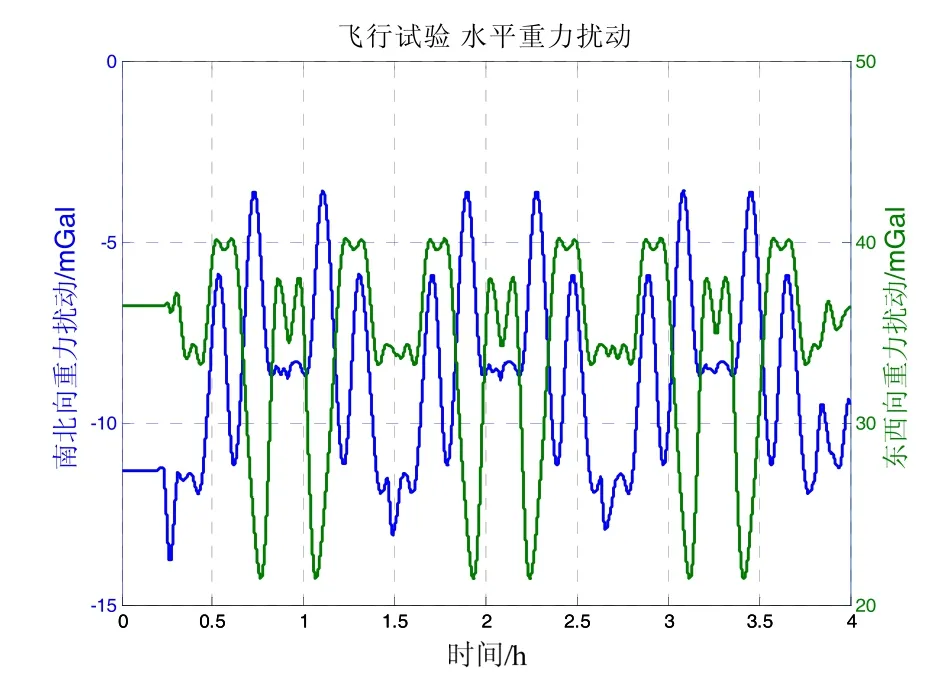
图5 飞行试验路径上的水平重力扰动Fig.5 Gravity disturbance on the airborne trajectory

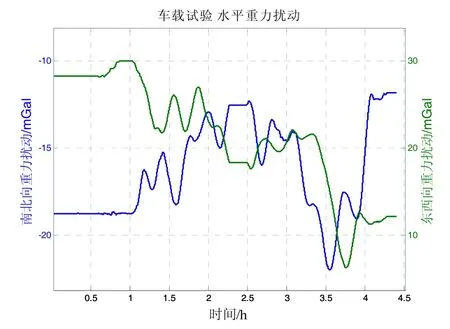
图6 车载试验路径上的水平重力扰动Fig.6 Gravity disturbance on the terrestrial trajectory

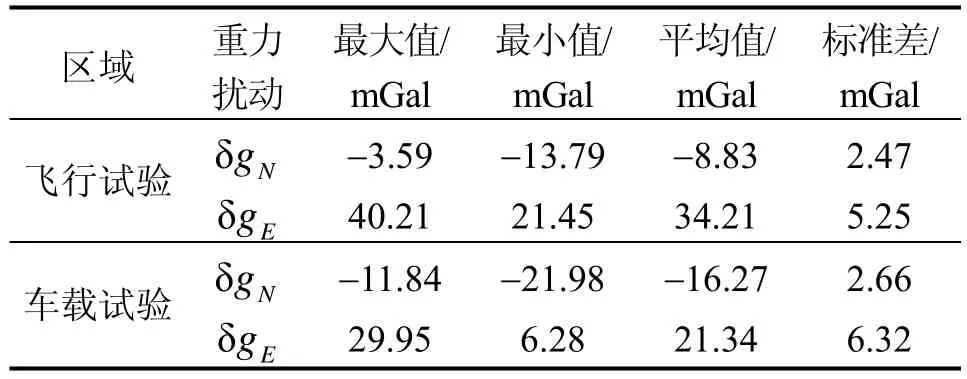
表3 飞行、车载试验 水平重力扰动统计值Tab.3 Statistical value of gravity disturbance

由水平重力扰动计算结果及正常重力构成重力矢量用于惯性导航，以差分GPS定位结果作为位置基准，得到未补偿及补偿后的惯性导航位置误差，用未补偿情况的位置误差减去补偿后的位置误差，如图7～8所示。

文献[4]中定量分析了在4 h惯性导航条件下，在一般区域及异常较大区域，水平重力扰动对惯性导航精度的影响，飞行及车载试验的惯性导航时间也恰好是4 h，因此文献[4]中的仿真分析结论对此处的实际数据计算结果分析有较大参考意义。将表3统计结果与文献[4]进行比较，飞行及车载试验区域应属于文献[4]所定义的水平重力扰动一般区域，在水平重力扰动一般区域，水平重力扰动造成的惯性导航位置误差在百米量级。如图6～7所示，4 h飞行及车载试验中，在使用计算的水平重力扰动数据对惯性导航进行补偿后，惯性导航定位精度最大提高120 m及110 m，与文献[4]中的仿真分析结论一致。为进一步验证长航时情况下水平重力扰动数据对惯性导航精度的提升效果，使用南海某海域24 h船载激光捷联惯导系统试验数据进行验证，使用GPS精密单点定位结果作为位置基准，使用位置基准信息及所述方法计算航路上的水平重力扰动数据，如图9、表4所示。

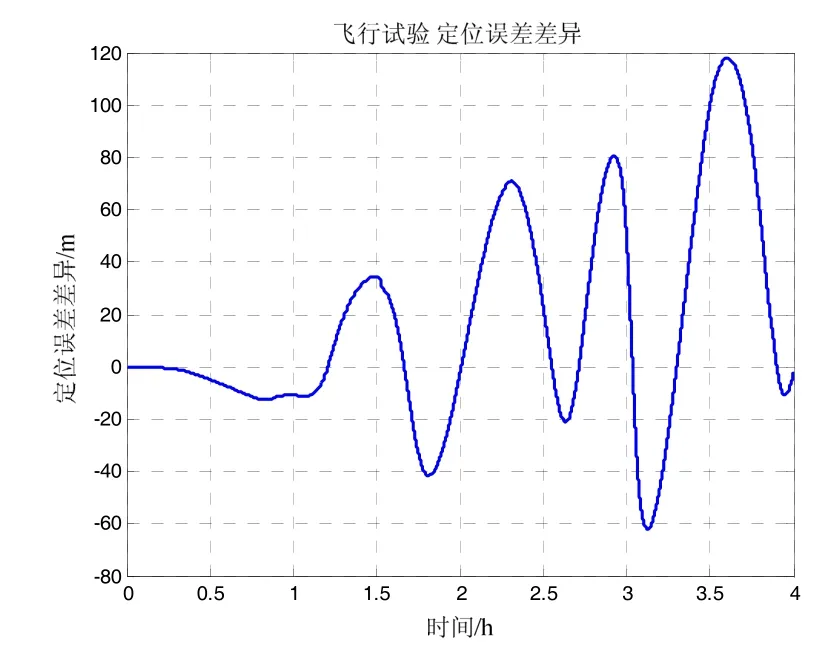
图7 飞行试验 补偿前后定位误差比较Fig.7 Position error comparison of airborne test

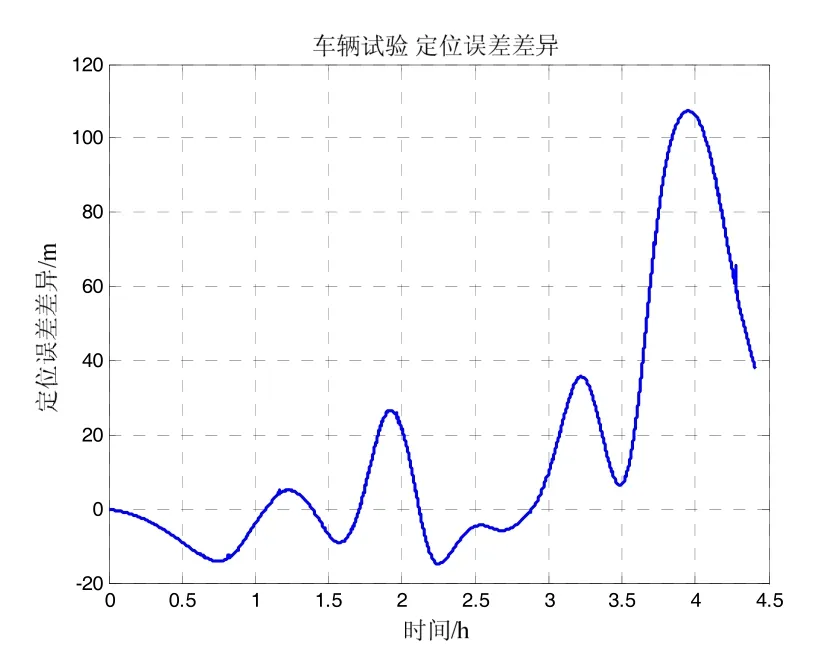
图8 车载试验 补偿前后定位误差比较Fig.8 Position error comparison of terrestrial test

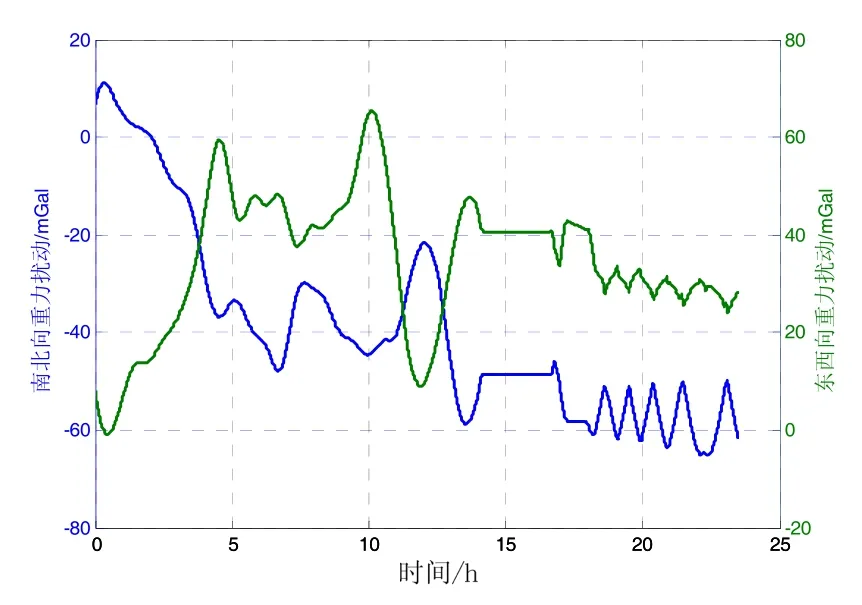
图9 船载试验路径上的水平重力扰动Fig.9 Gravity disturbance on the shipborne trajectory

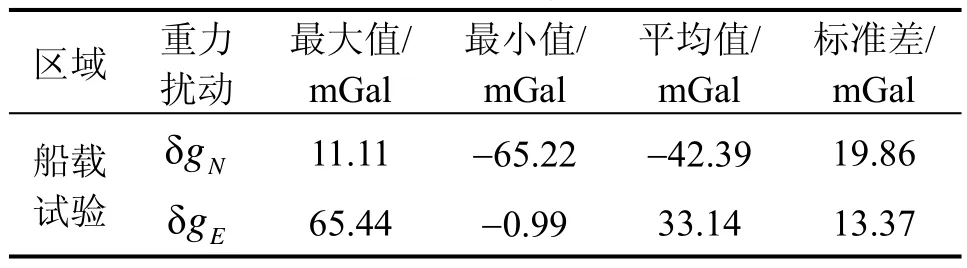
表4 船载试验中水平重力扰动统计值Tab.4 Statistical value of gravity disturbance

图10 船载试验 北向误差对比Fig.10 Latitude error comparison of shipborne test

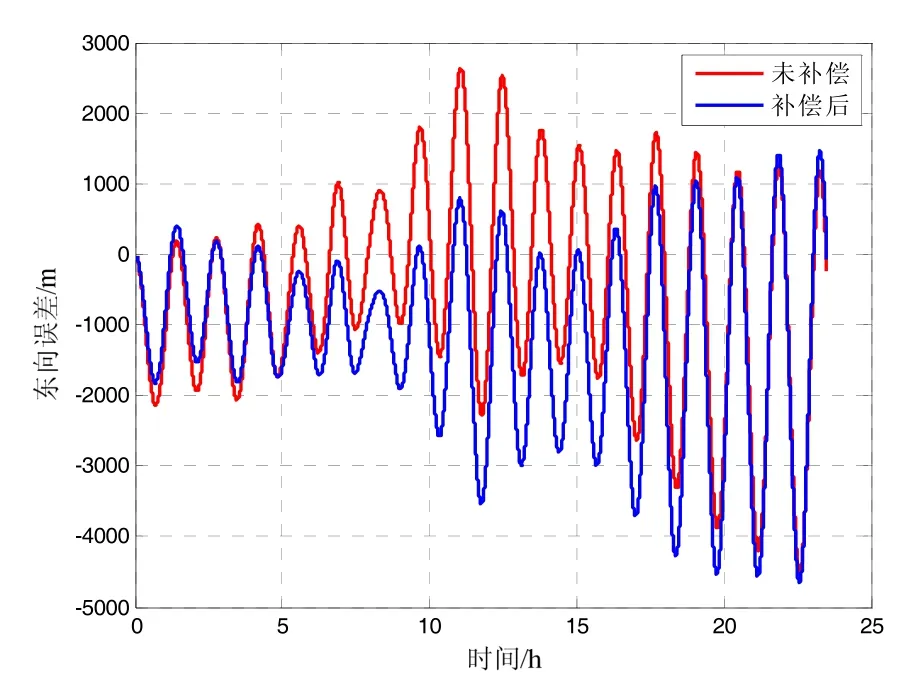
图11 船载试验 东向误差对比Fig.11 Longitude error comparison of shipborne test

使用水平重力扰动数据构建重力矢量用于惯性导航，将补偿后位置误差与未补偿时的位置误差对比，纬度误差、经度误差及位置误差对比如图10～12所示。由误差对比图可以看出，在使用了水平重力扰动数据补偿后，惯性导航精度高于使用正常重力模型情况，因此认为所计算的水平重力扰动数据可用于提高长航时惯性导航精度。对比表3、表4可以看到，相比于航空、车载试验区域，船载试验区域的水平重力扰动变化更大，因此使用水平重力扰动数据补偿后，惯性导航系统精度提升更加明显。

为定量评估垂线偏差数据对长航时船载惯性导航系统精度补偿效果，将图12中补偿前后在时间上对应的最大位置误差相减作为评估的依据，惯性导航精度最大提升1.5 n mile，平均提升0.8 n mile。

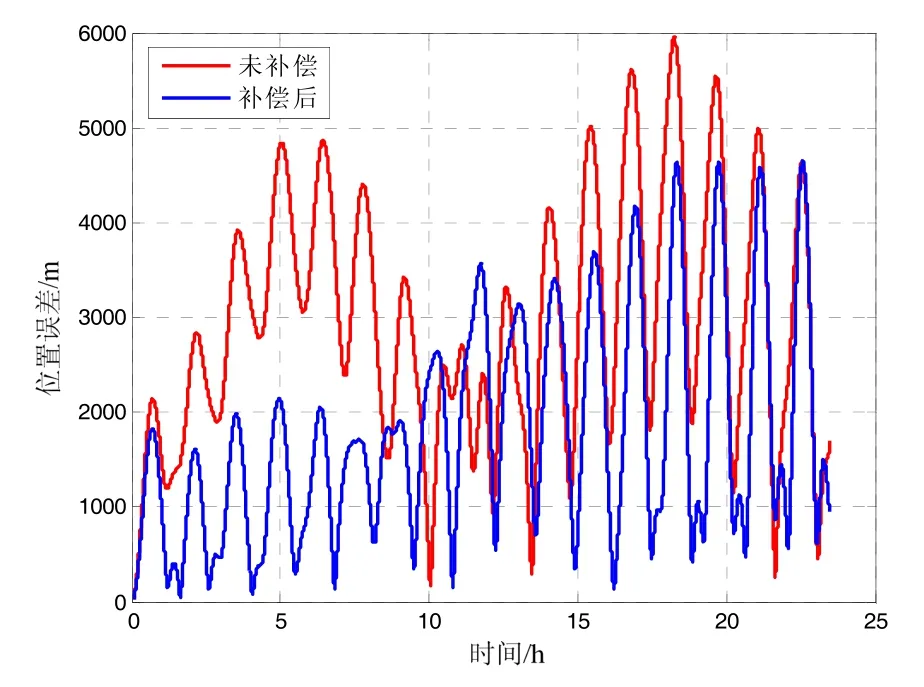
图12 船载试验位置误差对比Fig.12 Position error comparison of shipborne test

5 结 论

为解决高精度惯性导航对水平重力扰动数据需求，阐明了使用 EGM2008重力场球谐模型计算水平重力扰动的方法，水平重力扰动计算结果与 NGA官方提供的网格数据基本一致。

将水平重力扰动计算结果用于航空、车载及船载激光捷联惯性导航系统数据离线处理，计算结果表明，使用所述的水平重力扰动数据计算方法得到的水平重力扰动数据可用于提升惯性导航精度。

（References）：

[1]Hofmann-Wellenhof B, Moritz H.Physical geodesy[M].Austria: Springer-Verlag Wien, 2006.

[2]张开东.基于 SINS/DGPS的航空重力测量方法研究[D].长沙: 国防科学技术大学, 2007.Zhang K D.Research on the methods of airborne gravimetry based on SINS/DGPS[D].Changsha: National University of Defense Technology, 2007.

[3]蔡劭琨.航空重力矢量测量及误差分离方法研究[D].长沙: 国防科学技术大学, 2014.Cai S K.The research about airborne vector gravimeter and methods of errors separation[D].Changsha: National University of Defense Technology, 2014.

[4]赵忠, 王鹏.高精度惯性导航系统垂线偏差影响与补偿[J].中国惯性技术学报, 2013, 23(6): 701-705.Zhao Z, Wang P.Analysis and compensation of vertical deflection effect on high accuracy inertial navigation system[J].Journal of Chinese Inertial Technology, 2013,23(6): 701-705.

[5]周潇, 杨功流, 蔡庆中.基于小波神经网络的高精度惯导重力扰动补偿方法[J].中国惯性技术学报, 2016,24(5): 571-576.Zhou X, Yang G L, Cai Q Z.Compensation on gravity disturbance for high-precision INS based on wavelet neural network[J].Journal of Chinese Inertial Technology,2016, 24(5): 571-576.

[6]何昆鹏, 王晓雪.重力扰动对高精度惯性导航初始对准的影响与补偿[J].导航与控制, 2015, 14(5): 84-88.He K P, Wang X X.The effect of gravity disturbance on high-precision inertial navigation system[J].Navigation and Control, 2015, 14(5): 84-88.

[7]Wang J, Yang G L, Li X Y, et al.Application of the spherical harmonic gravity model in high precision inertial navigation systems[J].Measurement Science and Technology, 2016, 27: 095103(1-10).

[8]魏子卿.完全正常化缔合勒让德函数及其导数与积分的递推关系[J].武汉大学学报(信息科学版), 2016,41(1): 27-36.Wei Z Q.Recurrence relations for fully normalized associated legendre functions and their derivatives and integrals[J].Geomatics and Information Science of Wuhan University, 2016, 41(1): 27-36.

[9]Jekeli C, Lee J K, Kwon J H.On the computation and approximation of ultra-high-degree spherical harmonic series[J].Journal of Geodesy, 2007, 81(9): 603-615.

[10]http://earth-inf.nga.mil/GandG/wgs84/gravitymod/egm2008.

[11]Rapp R H.A FORTRAN program for the computation of gravimetric quantities from high degree spherical harmonic expansions[R].Department of Geodetic Science and Surveying, The Ohio State University, 1982.

[12]Colombo O L.Numerical methods for harmonic analysis on the sphere[R].Department of Geodetic Science and Surveying, The Ohio State University, 1981.

[13]Singh A.On numerical evaluation of normalized associated legendre functions[R].Department of Geodetic Science and Surveying, The Ohio State University, 1982.

[14]Titterton D H.Strapdown inertial navigation technology[M].2nd Edition.American Institute of Aeronautics and Astronautics, Inc., 2004.

[15]Wu R N, Wu Q P, Han F T, et al.Gravity compensation using EGM2008 for high-precision long-term inertial navigation systems[J].Sensors, 2016, 16: 2177.

[16]Zhou X, Yang G L, Cai Q Z, et al.A novel gravity compensation method for high precision free-INS based on extreme learning machine[J].Sensors, 2016, 16: 2019.

[17]Zhou, X Yang G L, Wang J, et al.An improved gravity compensation method for high-precision free-INS based on MEC-BP-AdaBoost[J].Measurement Science and Technology, 2016, 27: 125007.

[18]Fang J C, Chen L Z, Yao J F.An accurate gravity compensation method for high-precision airborne POS[J].IEEE Transactions on Geoscience and Remote Sensing,2014, 52(8): 4564-4573.

[19]Dai D, Wang X, Zhan D, et al.An improved method for dynamic measurement of deflections of the vertical based on the maintenance of attitude reference[J].Sensors, 2014,14: 16322-16342.

[20]Dai D, Wang X, Zhan D, et al.Dynamic measurement of high-frequency deflections of the vertical based on the observation of INS/GNSS integration attitude error[J].J.Appl.Geophys, 2015, 119: 89-98.

[21]Zhu J, Zhou Z B, Li Y, et al.Further development of the attitude difference method for estimating deflections of the vertical in real time[J].Measurement Science and Technology, 2016, 27: 075004.

Gravity disturbance calculation method based on Earth Gravitational Model 2008

TIE Jun-bo1, WU Mei-ping1, CAI Shao-kun1, ZHANG Kai-dong1, LIAN Jun-xiang1
(College of Mechatronics Engineering and Automation, National University of Defense Technology,Changsha 410073, China)

Vertical deflection can be used to improve the performance of inertial navigation system.The calculation method of vertical deflection based on harmonic model is described.EGM2008 is used to calculate vertical deflection.Comparison between the calculation result and 2.5′ 2.5′× DOV grid data from NGA verifies the validity of the described calculation method.Through the airborne and terrestrial strapdown inertial navigation calculation, it is shown that the gravity disturbance from EGM2008 can be used to improve the position accuracy of inertial navigation system, and the maximum and average location accuracies of inertial navigation system are increased by 1.5 n mile and 0.8 n mile, respectively, in the longtime shipborne test.

inertial navigation; gravity disturbance; gravity harmonics model; compensation for vertical deflection

U666.1

A

1005-6734(2017)05-0624-06

10.13695/j.cnki.12-1222/o3.2017.05.012

2017-05-27；

2017-09-11

国家自然科学基金项目（61603401）；国土资源部航空地球物理与遥感地质重点实验室 青年创新基金课题（2016YFL06）

铁俊波（1989—），男，博士研究生，从事惯性导航系统研究。E-mail: tiejunbo11@nudt.edu.cn

联 系 人：吴美平（1970—），男，教授，博士生导师。E-mail: meipingwu@263.net