存在部分连通断层的线性复合油藏井底压力动态研究

曾 杨, 康晓东, 谢晓庆, 石 爻, 张烈辉

(1.海洋石油高效开发国家重点实验室，北京 100028; 2.中海油研究总院，北京 100028；3.油气藏地质及开发工程国家重点实验室(西南石油大学)，成都 610500)

存在部分连通断层的线性复合油藏井底压力动态研究

曾 杨1,2, 康晓东1,2, 谢晓庆1,2, 石 爻1,2, 张烈辉3

(1.海洋石油高效开发国家重点实验室，北京 100028; 2.中海油研究总院，北京 100028；3.油气藏地质及开发工程国家重点实验室(西南石油大学)，成都 610500)

针对存在部分连通断层的线性复合油藏研究较少，用现有的试井解释模型对具有部分连通断层边界的油藏试井资料进行解释所得到的结果不理想的现状，本文引入界面表皮概念，将部分连通断层视为一个无限薄的表皮边界，建立了两区无限大线性复合油藏中存在部分连通断层的试井解释模型，并利用Fourier指数变换和Laplace变换等方法进行求解，绘制了井底压力响应特征曲线，并用实例对模型进行验证。分析表明，界面表皮越大，曲线上翘越多，当它足够大时，表现为封闭断层的特征；厚度比、流度比越大，曲线表现出定压边界的特征；导压系数比越小，Ⅱ区的储集能力越大，相应的压力及压力导数曲线位置越靠下。

部分连通断层；线性复合；界面表皮；试井模型；典型曲线

国内外众多学者对断层边界的试井研究主要是将断层视为无流体流动的封闭边界[1-7]，而对非封闭断层即部分连通断层的研究较少。常用于判别封闭断层的方法就是D.R.Horner[8]半对数曲线法。R.K.Prasad[9]将存在一条封闭断层边界的模型扩展到多条交叉或者平行的封闭断层模型；H.C.Bixel等[10]首次提出将断层视为非封闭边界，但所建立的模型仅仅考虑岩石和流体性质在平面上发生突然变化的情形；F.J.Kuchuk等[11]后来对该模型的求解方法进行了完善。G.Stewart等[12]和T.D.Streltsova等[13]在H.C.Bixel等[10]研究的基础上通过数值模拟研究了部分连通断层对干扰试井的影响；L.M.Yaxely[14]推导了无限大均质油藏中含有部分连通断层模型的解析解；B.Abdelaziz[15]在L.M.Yaxely[14]的基础上研究了均质油藏中存在2条交叉断层边界的压力动态特征。A.K.Ambastha等[16]进一步研究了复合油藏中存在部分连通断层边界的井底压力响应特征，但他仅针对径向复合油藏，并没有对线性复合油藏进行研究。虽然张望明等[17]引入偏移函数的概念建立了存在一条局部连通断层边界的线性复合油藏试井解释模型，但未考虑断层两侧储层不等厚的情形，且求解过程复杂。为此，本文通过引入A.F.Everdingen[18]和W.Hurst[19]提出的界面表皮的概念，将部分连通断层视为一个无限薄的表皮边界，建立存在部分连通断层的两区无限大线性复合油藏试井解释新模型，绘制模型的井底压力响应特征曲线，并对相关的影响因素进行分析。

1 渗流物理模型

针对两区无限大线性复合油藏中存在部分连通断层的情形(图1)，假设断层两侧的岩石特性、储层厚度及渗透率不同，但同一区域内为均质油藏且各向同性。激动井为定产量线源，各区流体只能通过裂缝流向井筒，且流体为微可压缩等温渗流。引入界面表皮的概念考虑2个储层区域之间断面的传导率，忽略重力和毛管力的影响。

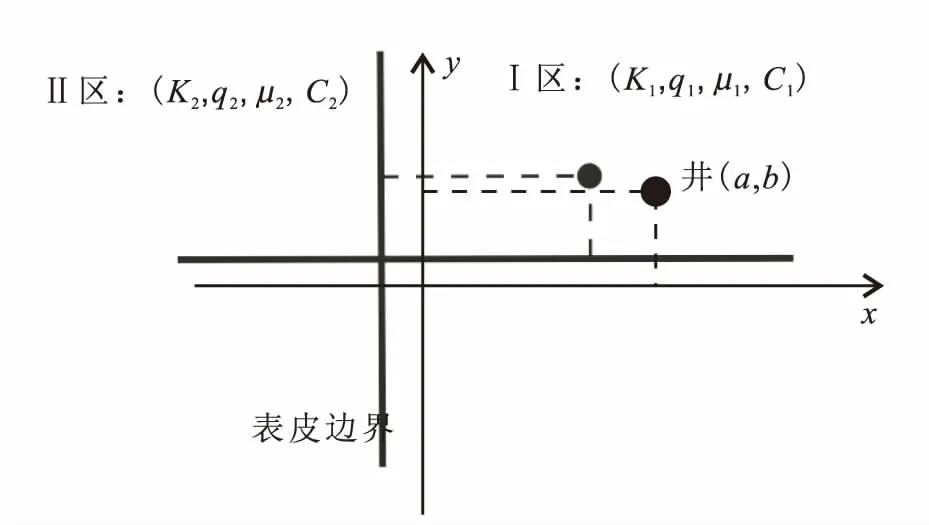
图1 存在部分连通断层的两区无限大线性复合油藏示意图Fig.1 Sketch showing the partially connected fault system in linear composite reservoir

2 数学模型及求解

2.1 数学模型的建立

根据图1所建立的坐标系和上述假设条件，以基本的渗流力学理论为依据，可推导出两区无限大线性复合油藏中存在部分连通断层的无因次试井解释模型。

a.渗流微分方程

Ⅰ区，对于xDgt;0

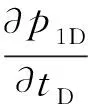
(1)

Ⅱ区，对于xDlt;0

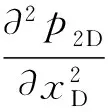
(2)

式中的无因次变量分别为

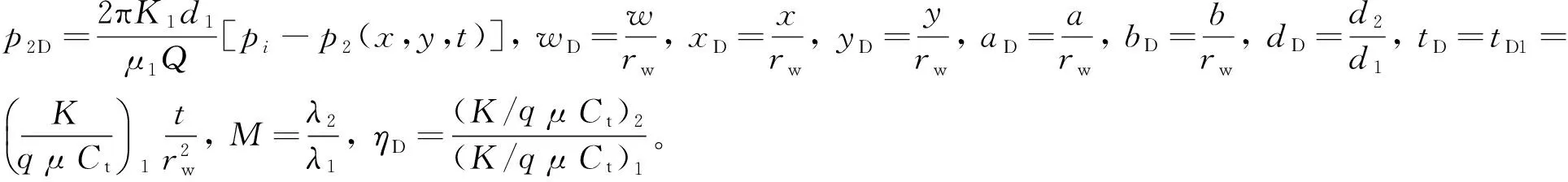
b.初始条件

p1D(xD,yD,0)=p2D(xD,yD,0)=0

(3)

c.边界条件

p1D(∞,yD,tD)=p2D(-∞,yD,tD)

=p1D(xD,±∞,tD)=p2D(xD,±∞,tD)

=0

(4)

d.连接条件

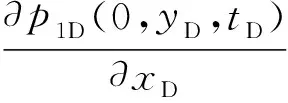
(5)

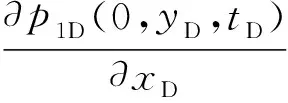
p1D(0,yD,tD)]

(6)

其中S表示断层的界面表皮。

2.2 数学模型的求解

对上述无因次试井模型(1)式～(6)式取基于yD的Fourier指数变换和基于tD的Laplace变换并化简，可得

(7)

求解可得

(8)

(9)

将α3代入式(9)并进行Fourier逆变换，令xD=aD-1，yD=bD，得

(10)

式中

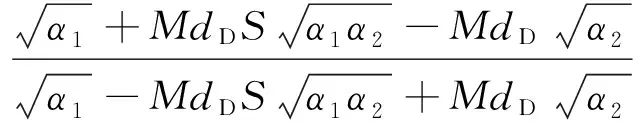
(11)

3 典型曲线的绘制及特征分析

根据求得的Laplace空间井底压力表达式，采用Stehfest数值反演方法对其进行Laplace逆变换，利用计算机编程技术，绘制两区无限大线性复合油藏中存在部分连通断层边界的井底压力响应特征曲线。下面对典型曲线特征及主要影响因素进行分析。

3.1 界面表皮的影响

图2表示在无限大复合油藏中存在部分连通断层时，部分连通断层的界面表皮(S)对井底压力动态特征的影响。从图中可知，无论S取值如何，典型曲线早期都表现出井储阶段的特征，压力与压力导数曲线重合，二者均为斜率=1的直线。随着压力波的不断向外传播，当tD较小时，压力波尚未传播到两区分界面，压力导数曲线表现为均质油藏渗流特征的0.5水平线，该阶段持续时间的长短取决于aD值的大小。随着tD不断增大，压力波传播到两区分界面处，当S=0时，分界面处无压降，压力导数曲线继续表现为0.5水平线。当Sgt;0时，Ⅰ区与Ⅱ区的连通性减弱，流体在地层中流动的压力损失就增大，压力导数曲线逐渐上翘，并且S值越大，曲线上翘得越多；随后，随着压力波传过界面，整个油藏渗流表现出均质油藏的特征，压力导数曲线为0.5水平线。特别地，当S=106时，此时接近于封闭断层，压力导数曲线表现出封闭断层的特征，即值为1的水平线。

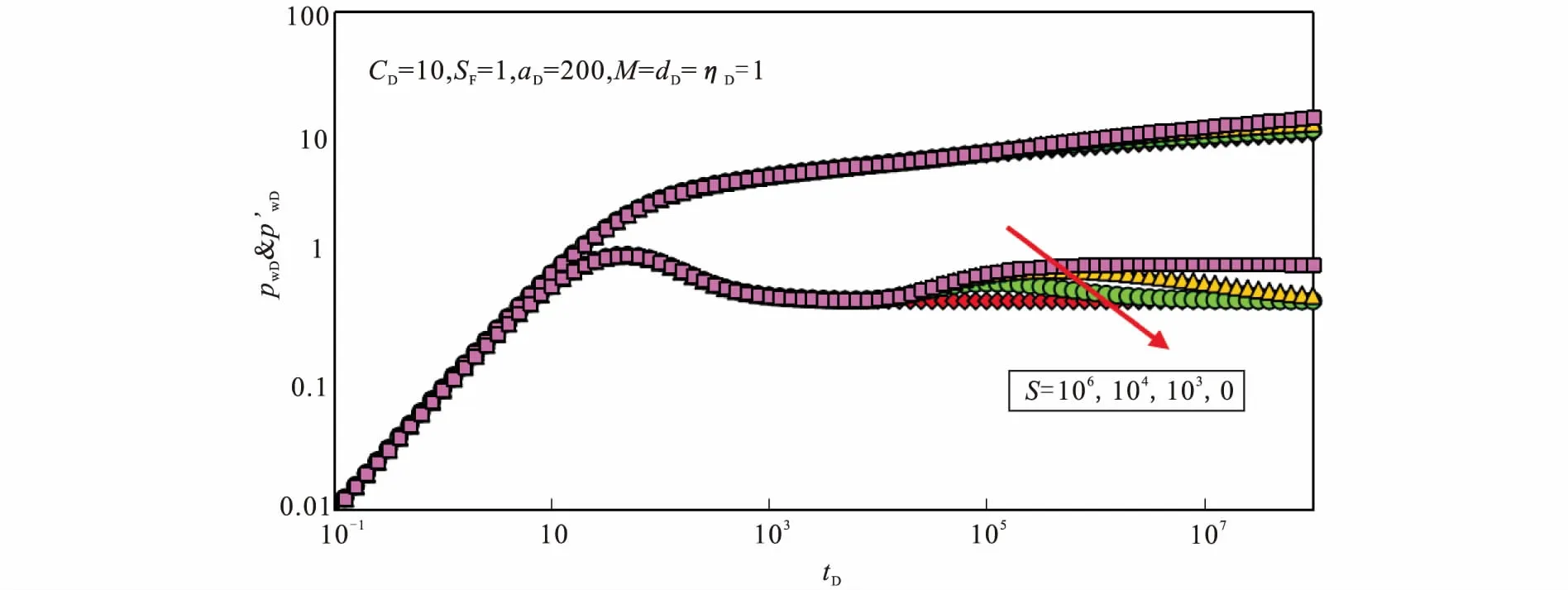
图2 界面表皮对典型曲线的影响Fig.2 Effect of the boundary skin on the calculated typical dimensionless curves

3.2 流度比的影响

图3表示的是当部分连通断层的界面表皮S=1 000时，流度比(M)对井底压力动态曲线的影响。从图中可以看出，经过井储和径向流阶段后，由于分界面处界面表皮的存在，流体在地层中流动的压力损失就增大，压力导数曲线先从0.5水平线开始上翘。随后随着流度比的增加，地层的平均流动性变好，无因次压力及压力导数曲线就会降低；且流度比越大，压力及压力导数曲线的位置越靠下。当M≫1，相当于定压边界；当M≪1，相当于封闭边界。

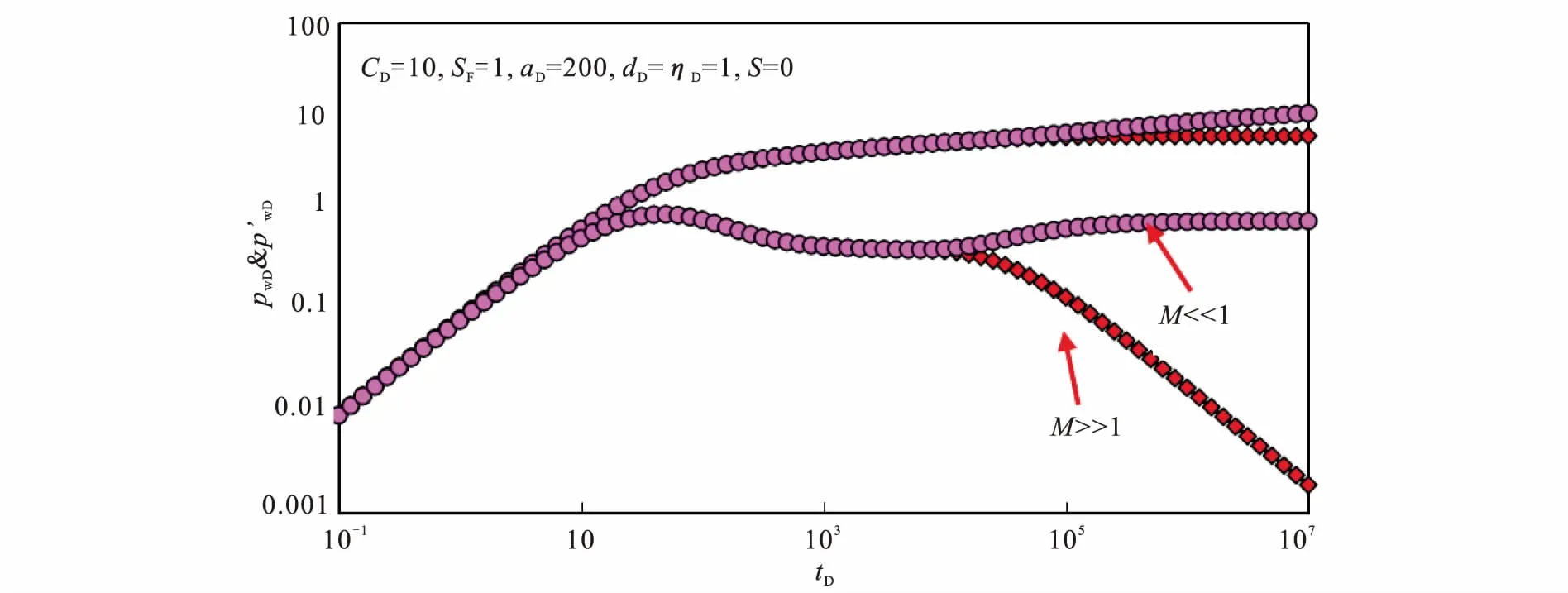
图3 流度比对典型曲线的影响Fig.3 Effect of the mobility ratio on the calculated typical dimensionless curves

3.3 厚度比的影响

图4显示了厚度比(dD)对油藏中的井底压力动态曲线的影响。从图中可以看出，厚度比dD对井底压力动态的影响与流度比M对井底压力动态的影响类似。dD越大，说明Ⅱ区地层供给能力越强，流体在地层中流动的压力损失就越小，反映等效均质储层径向流的第二个压力导数水平段位置就越低。

3.4 导压系数比的影响

图5显示了导压系数比(ηD)对油藏中的井底压力动态曲线的影响。从图中可以看出，ηD对典型曲线形态的影响主要发生在压力波传播到区域交界面之后。其他参数一定的情况下，ηD越小，说明Ⅱ区的储集能力越大，压降就越小，相应的压力及压力导数曲线位置越靠下。当存在界面表皮时，压力波传播到区域交界面，由于界面表皮的存在，流体流动阻力增加，压降增加，压力导数曲线先上翘，继而才反映出导压系数比的影响。

4 实例分析

某油田的某生产井进行了压力恢复测试，该井在测试前以320 m3/d的产量生产了540 h。相关参数如下：井径为0.08 m，孔隙度为0.13，综合压缩系数为4.81×10-3MPa-1，原油黏度为0.22 mPa·s，体积系数为2.31，关井前井底流压为25.61 MPa，井两侧油藏厚度差异较大，有效厚度比为5。

绘制实测压力数据双对数图，结合该区的地质特征，用现有的比较接近实测曲线特征的模型[17]进行拟合(图6)，可以看出拟合效果不好，实测数据压力导数曲线后期靠下，类似定压边界，因此采用文中提出的模型进行拟合，拟合效果较好(图7)。

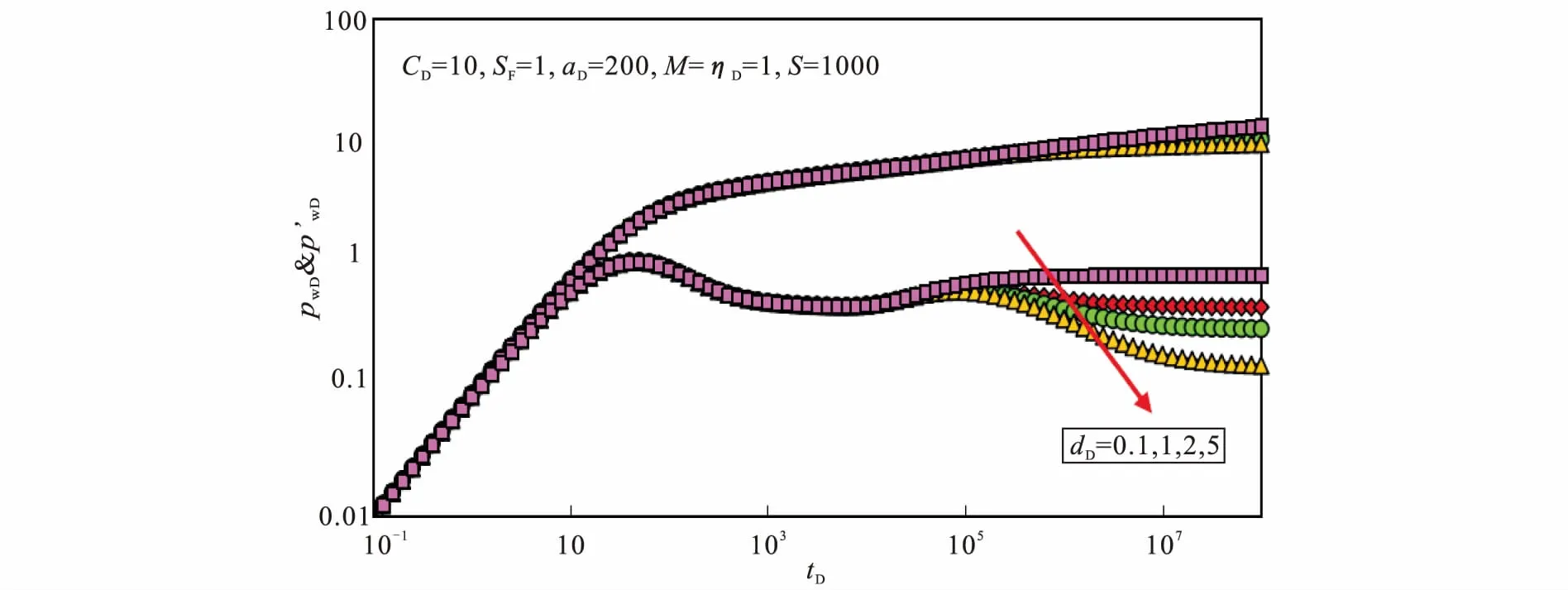
图4 厚度比对典型曲线的影响Fig.4 Effect of the thickness ratio on the calculated typical dimensionless curves

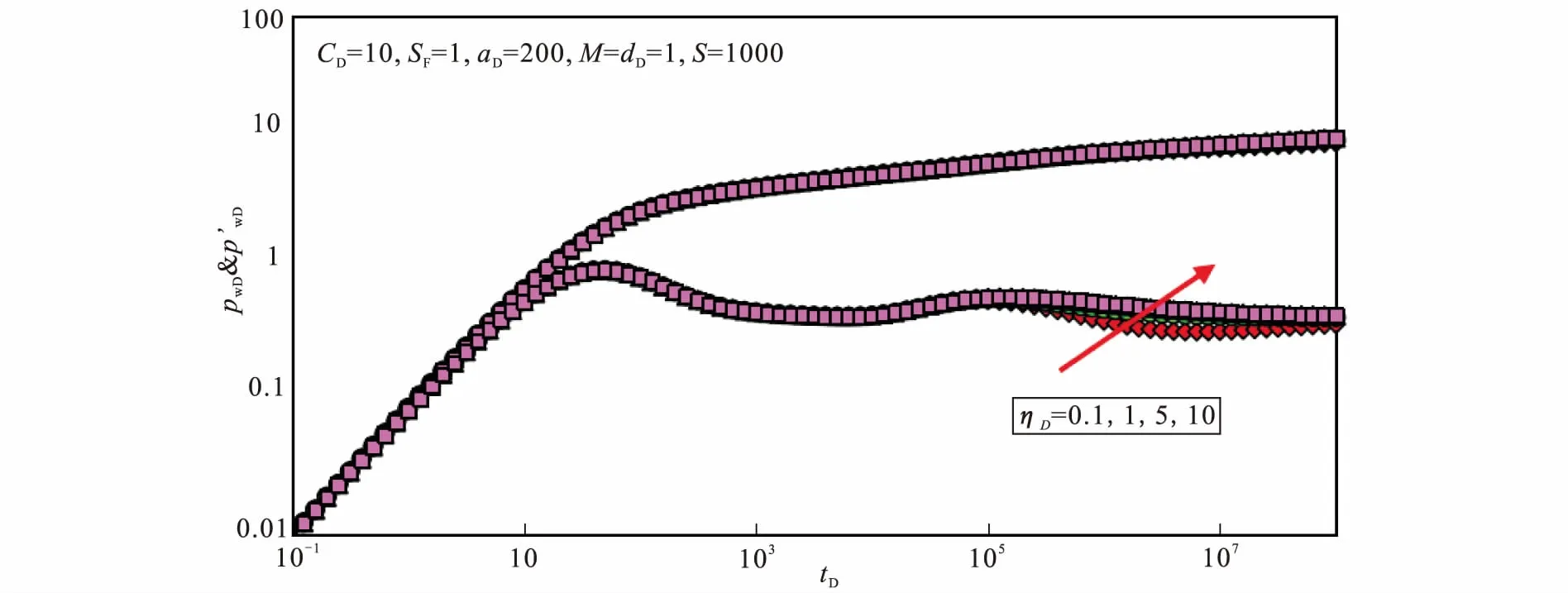
图5 导压系数比对典型曲线的影响Fig.5 Effect of the pressure coefficient ratio on the calculated typical dimensionless curves

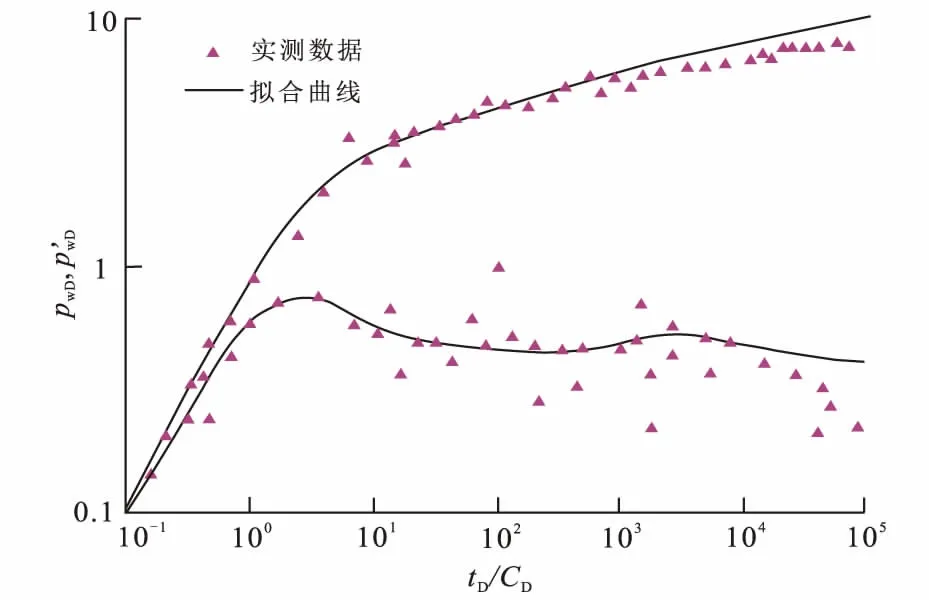
图6 实例井测试数据与文献图版拟合曲线Fig.6 Matching curves of field test data with reference model

根据实测曲线与理论典型曲线拟合图，得出拟合结果为：井筒储集系数0.26 m3/MPa，表皮系数-2.41，渗透率10.25×10-3μm2，井到断层的距离为78.98 m，断层的界面表皮为80。

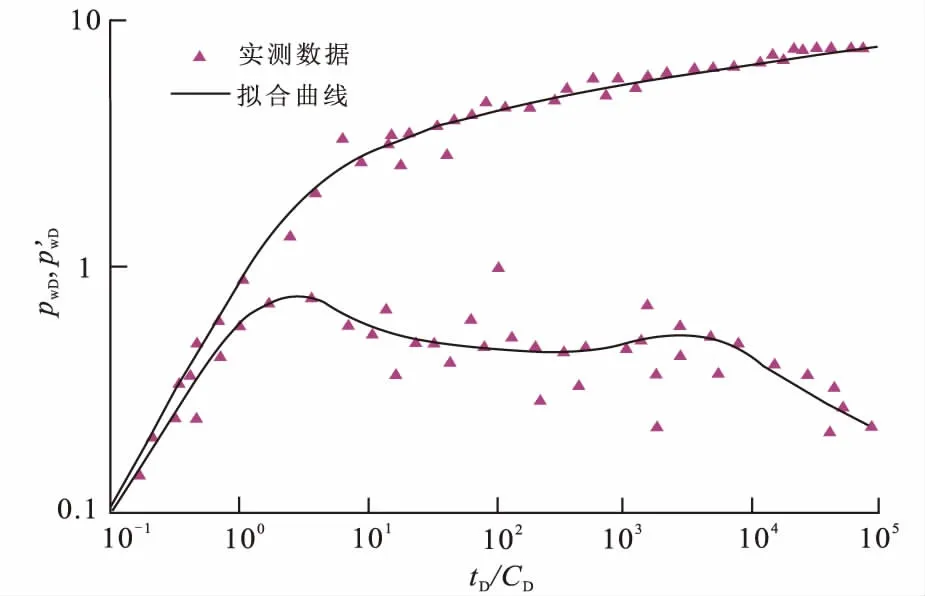
图7 实例井测试数据与本文图版拟合曲线Fig.7 Matching curves of field test data with proposed well testing model

5 结 论

a.引入界面表皮，建立了无限大线性复合油藏中存在部分连通断层边界的试井解释新模型，对具有类似边界条件的油藏研究和应用具有一定的借鉴意义。

b.界面表皮越大，流体流动的阻力越大，无因次压力及压力导数曲线位置越靠上，当界面表皮足够大时，表现为封闭断层的特征。当M≫1，表现出定压边界的特征；当M≪1，表现出封闭边界的特征。厚度比对井底压力动态的影响与流度比类似。导压系数比越小，Ⅱ区的储集能力越大，相应的压力及压力导数曲线位置越靠下。

c.本文提出的断层模型可用于双重介质油藏、条带状油藏等的试井解释及压力分布规律研究。

[1] Tiab D. Analysis of Multiple-Sealing-Fault Systems and Closed Rectangular Reservoirs by Type Curve Matching[D]. Norman: The University of Oklahoma, 1976.

[2] Tiab D, Kumar A. Detection and location of two parallel sealing faults around a well[J]. JPT, 1980, 32(10): 1701-1708.

[3] Tiab D, Crichlow H B. Pressure analysis of multiple-sealing-fault systems and bounded reservoirs by type curve matching[J]. SPEJ, 1979, 19(6): 378-392.

[4] Chen H K, Brigham W E. Pressure buildup for a well with storage and skin in a closed square[J]. JPT, 1978, 30(1): 141-146.

[5] Van Poollen H K. Drawdown curves give angle between intersecting faults[J]. The Oil amp; Gas Journal, 1965, 63(51): 71-75.

[6] Ispas V, Tiab D. New method of analyzing the pressure behavior of a well near multiple boundary systems[C]//Presented at the 1999 Latin American and Caribbean Petroleum Engineering Conference. Venezuela: Society of Petroleum Engineers, 1999: 111-123.

[7] 刘能强.实用现代试井解释方法[M].北京:石油工业出版社,1996:28-55.

Liu N Q. Practical Modern Well Testing Interpretation Method[M]. Beijing: Petroleum Industry Press, 1996: 28-55. (in Chinese)

[8] Horner D R. Pressure build-up in wells[C]//3rd World Petroleum Conference. Netherlands: Society of Petroleum Engineers, 1951: 503-521.

[9] Prasad R K. Pressure transient analysis in the presence of two intersecting boundaries[J]. JPT, 1975, 27(1): 89-96.

[10] Bixel H C, Larkin B K, Van Poolen H K. Effect of linear discontinuity on pressure buildup and drawdown behavior[J]. JPT, 1963, 15(8): 885-895.

[11] Kuchuk F J, Habashy T M. Pressure behavior of laterally composite reservoir[J]. SPEFE, 1997, 12(1): 47-56.

[12] Stewart G, Gupta A, Westaway P. The interpretation of interference tests in a reservoir with a sealing and a partially communicating faults[C]//Presented at the 1984 European Petroleum Conference. London: Society of Petroleum Engineers, 1984: 411-429.

[13] Streltsova T D, McKinley R M. Effect of flow time duration on buildup pattern for reservoirs with heterogeneous properties[J]. SPEJ, 1984, 24(3): 294-306.

[14] Yaxely L M. Effect of partially communicating fault on transient pressure behavior[J]. SPEFE, 1987, 2(4): 590-598.

[15] Abdelaziz B. Pressure behavior of a well between two intersecting leaky faults[C]//Presented at the 2004 Nigeria Annual International Conference and Exhibition. Abuja: Society of Petroleum Engineers, 2004: 122-134.

[16] Ambastha A K, McLeroy P G, Grader A S. Effect of a partially communicating fault in a composite reservoir on transient pressure testing[J]. SPEFE, 1989, 4(2): 210-218.

[17] 张望明,曾萍.存在局部连通断层的复合油藏不稳定试井分析及典型曲线拟合方法[J].石油勘探与开发,2008,19(2):69-76.

Zhang W M, Zeng P. Transient pressure testing analysis and type-curve matching in a composite reservoir with a partially communicating fault[J]. Petroleum Exploration and Development, 2008, 19(2): 69-76. (in Chinese)

[18] Everdingen A F. The skin effect and its influence on the productivity capacity of a well[J]. JPT, 1953, 5(6): 171-176.

[19] Hurst W. Establishment of the skin effect and its impediment to fluid flow in a wellbore[J]. Petroleum English, 1953, 25(8): 6-16.

Analysisoftransientpressurebehaviorinlinearcompositereservoirwithpartiallyconnectedfaults

ZENG Yang1,2, KANG Xiaodong1,2, XIE Xiaoqing1,2, SHI Yao1,2, ZHANG Liehui3

1.StateKeyLaboratoryofOffshoreOilExploitation,Beijing100028,China；2.CNOOCResearchInstitute,Beijing100028,China；3.StateKeyLaboratoryofOilandGasReservoirGeologyandExploitation,SouthwestPetroleumUniversity,Chengdu610500,China

The application of presently existing models of well testing analysis to actual well testing data with partially connected fault boundary usually resulted in unsatisfactory consequences. Therefore, a concept of “boundary skin” is proposed in which the partially connected fault is considered as an infinite thin boundary skin and a new well testing model for partially connected fault in a two-zone, linear composite reservoir is established. Fourier and Laplace transformations are used to calculate and obtain the solution, and to plot the responding typical curves of well bottom pressure. It shows that large boundary skin leads to the upward of curve. When the boundary skin is large enough, the partially connected fault is characteristic of close fault. If the ratio of thickness and ratio of mobility become larger, the typical curve demonstrates a character of stable pressure boundary. It reveals that the smaller the pressure coefficient ratio, the greater the storage capacity of the zone Ⅱ, and the lower the corresponding pressure and pressure derivative curve position.

partially connected fault; linear composite; boundary skin; well testing model; type curve

TE353

A

10.3969/j.issn.1671-9727.2017.06.06

1671-9727(2017)06-0691-06

2017-04-27。

国家科技重大专项(2016ZX05025-003); 中海石油(中国)有限公司综合科研项目(YXKY-2014-ZY-03)。

曾杨(1987-)，女，硕士，工程师，从事油气田开发及提高采收率研究工作, E-mail：zengyang@cnooc.com.cn。