可见光通信中LED的非线性后失真补偿技术研究*

徐旭东

(南京邮电大学 通信与信息工程学院，江苏 南京 210003)

可见光通信中LED的非线性后失真补偿技术研究*

徐旭东

(南京邮电大学 通信与信息工程学院，江苏 南京210003)

在可见光通信系统中，发光二极管(LightEmittingDiode，LED)的非线性特性是可见光通信系统存在非线性失真的主要原因。针对可见光通信的LED非线性失真的补偿技术的研究主要分为预失真补偿和后失真补偿技术。由于预失真方法需要在发送端增加一个物理反馈回路，因此这种方法的性价比并不高。与预失真方法相比，后失真方法从接收端对信号进行补偿，不需要额外的反馈回路。现有的后失真方法，如Volterra判决反馈均衡方法、自适应后失真补偿方法以及从频域均衡的角度对系统进行补偿的方法，都在很大程度上减轻了LED的非线性失真问题对可见光通信系统造成的影响。机器学习作为智能化的核心，将其与后失真技术相结合，同样可以在很大程度上减轻LED的非线性失真带来的影响。

后失真;Volterra判决反馈均衡;自适应后失真;频域均衡;机器学习

0 引言

随着LED越来越廉价，并且应用越来越广泛，针对可见光通信技术的研究也越来越多。可见光通信相比于传统的无线通信技术可以解决其带宽受限的问题，而且实现成本低，通信安全性和空间复用性都很高。与射频系统类似，可见光通信系统同样存在非线性失真问题。造成可见光通信系统非线性失真的原因可能有：LED电路、对发送信号进行剪切处理、数模转换、模数转换、LED本身特性以及光敏二极管的特性。由于可见光通信系统使用了密度调制和直接检测技术，因此光电转换和电光转换同样会带来非线性影响。但在这些可能的原因中，LED的非线性特性是造成可见光通信系统非线性失真的主要原因[1]，即经过LED发送之前的信号和接收端接收到的信号是非线性关系，在这种情况下会使信号的解码产生很大的困难和误码率。LED的非线性失真主要是因为发光子与输入电流的幅值不成比例，并且由于载流子密度响应由频率决定，从而又给LED带来了记忆性问题。

针对LED的非线性特性，可以根据其是否具有记忆性对其进行建模。无记忆的典型模型有无记忆多项式模型；有记忆的模型有Volterra模型[2]、记忆的多项式模型、Wiener模型[3]以及Hammerstein模型。通过Volterra序列可以很好地描述LED的非线性特性，但其结构相对复杂，随着模型层数的增加，参数的数量将会大大增加。记忆多项式模型是Volterra模型的一个特例，与无记忆多项式模型相比，其输入不仅取决于当前，还取决于之前的输入。Wiener模型也属于Volterra模型，其包含一个线性时不变模块和一个无记忆非线性模块。与Wiener模型相反，Hammerstein模型是无记忆非线性模块后面跟着一个线性时不变模块。Wiener模型和Hammerstein模型在一定程度上减小了模型的复杂度。

本文针对LED的非线性失真问题，总结了3种现有的后失真补偿方法，并且在QIAN H的方法的基础上提出了将后失真补偿技术与机器学习相结合，利用BP神经网络和支持向量机对LED的非线性失真进行后失真补偿。

1 现有的后失真补偿技术

图1 后失真补偿技术原理图

1.1Volterra判决反馈均衡

文献[4]中提出的方法是通过在接收器部分增加一个非线性Volterra序列的判决反馈均衡器来改善LED的非线性特性对可见光通信系统造成的影响,这种方法可以有效地补偿动态或静态的LED非线性，但结构较为复杂。文献[2]证明了用Volterra序列模型来描述LED的非线性特性的记忆性比一般的静态方法的可靠性要高，即和Wiener模型一样，Volterra模型同样可用来描述LED的非线性特性。换个方式考虑，即Volterra模型同样可以用来描述LED的反向特性。文献[4]中实验表明采用二级(或二级以上)的Volterra序列的判决反馈均衡器，就可以从光功率的角度将光功率提高5 dB。

图2为Volterra判决反馈均衡器的结构图，包括一个线性部分和一个前馈部分，其中前馈部分对应描述系统的Volterra级数。判决反馈均衡器的输出y(n)可以表式为:

(1)

其中：

(2)

(3)

(4)

其中x(n)是接收信号的样本，a(i)是线性均衡器的参数，b(i,j)和c(i,j,k)是二级和三级线性均衡器的参数，这些参数对应于均衡器的前馈部分。w(i)为反馈滤波器的参数，d(n)是训练信号序列。利用最小均方算法或者递推最小均方算法可以得到均衡器的最佳参数。

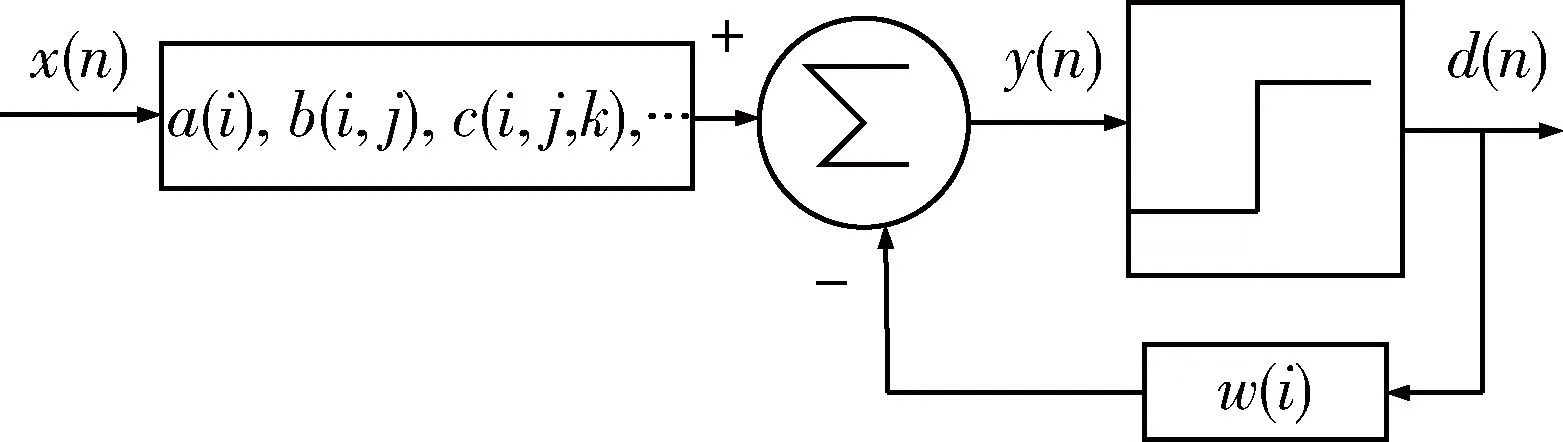
图2 Volterra判决反馈均衡结构图

与一般的判决反馈均衡器相比，Volterra判决反馈均衡器接收机考虑了记忆性，从而降低了系统误码率，同时，使用最小均方算法，提高了系统参数的收敛速度，从而进一步提高了系统的性能。但Volterra判决反馈均衡器的结构相对较为复杂。

1.2自适应后失真补偿

在文献[3]中，QIAN H等人提出了在接收器端采用一个反馈链路来自适应跟踪和补偿LED的非线性。其主要思想就是采用多项式模型作为后失真模块，通过将y(n)作为模型的输入，x(n)作为模型的输出，训练模型得到模型的参数，从而确定模型。多项式模型不仅可以保证自适应后失真技术的鲁棒性，而且可以将系统的记忆性考虑在内。文献[3]中使用Wiener模型来模拟LED的非线性特性，同时使用DCO-OFDM来对发送信号进行调制，以减少LED的记忆性带来的符号间干扰。

图3为Wiener模型的结构示意图，Wiener模型包含一个线性时不变模块和一个无记忆非线性模块。其中线性时不变部分可以描述为下面的数学表达式：

(5)

其中L是最大时延。

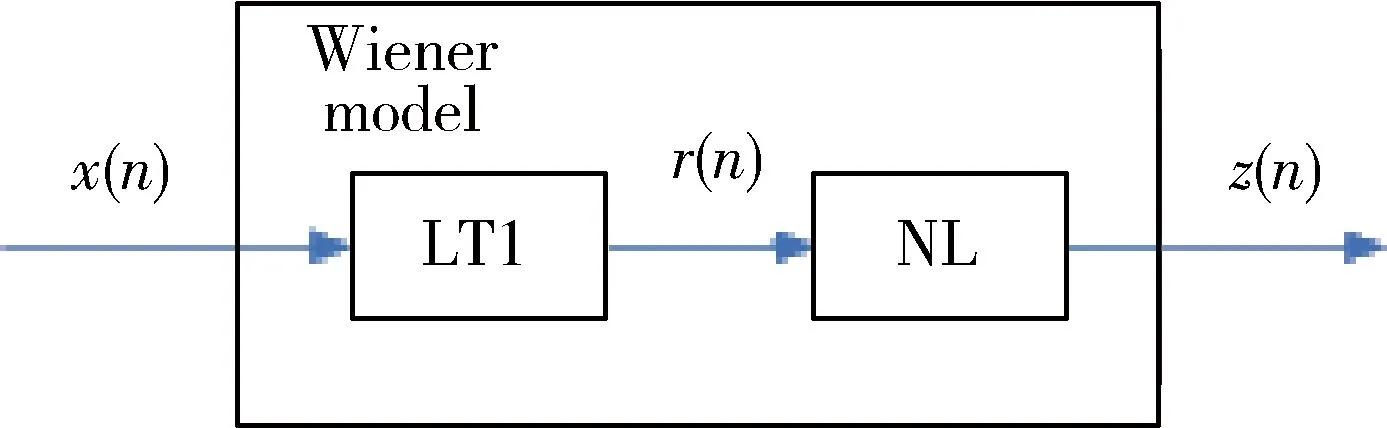
图3 Wiener模型结构图

无记忆非线性部分可以用Rapps模型来表示，Rapps模型通常被用来在射频系统中模拟功率放大器的非线性特性。因此，LED的电流-电压非线性可以表示为:

z(n) =

(6)

其中Imax是LED允许通过的最大电流，k是保持曲线平滑的系数。

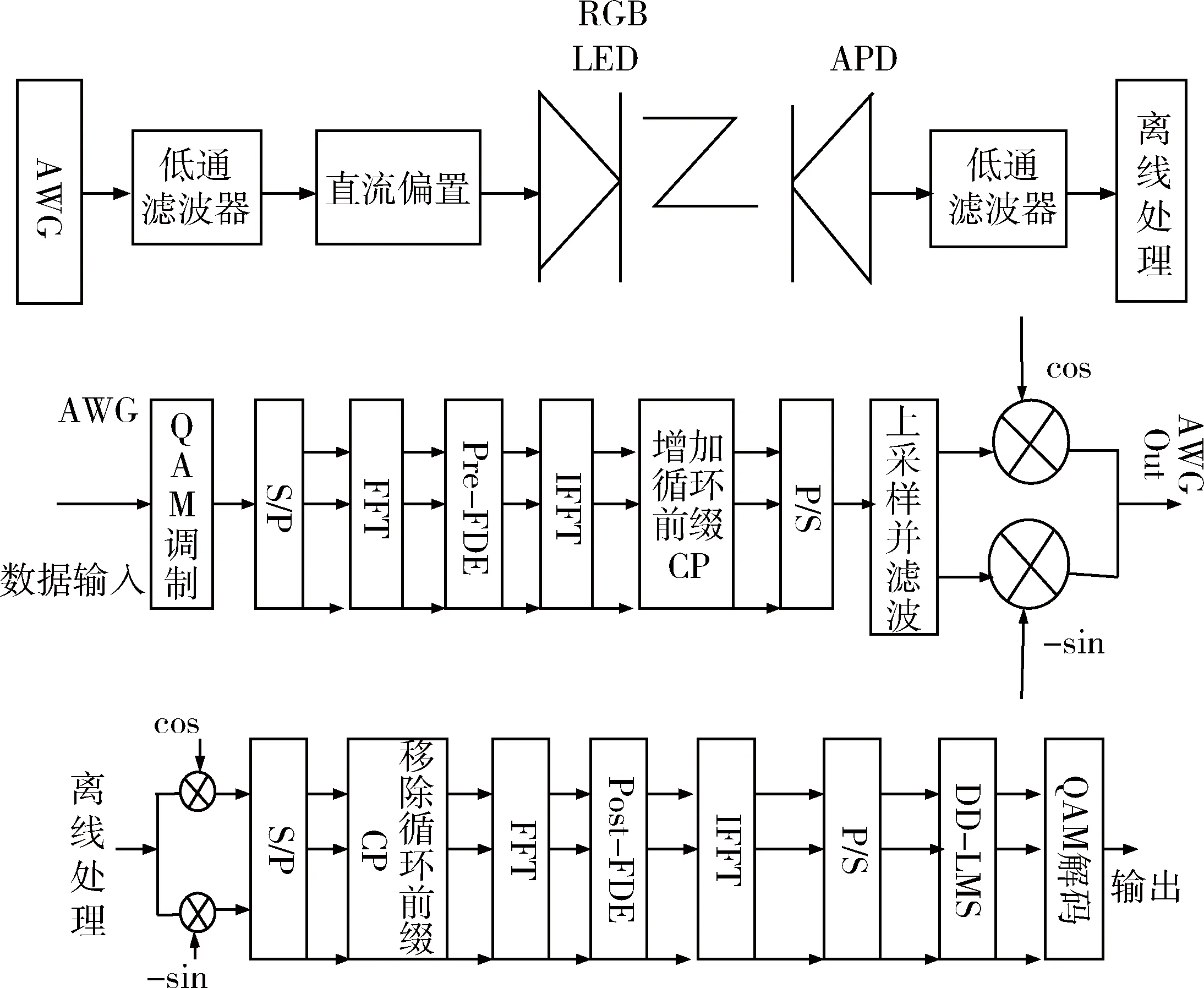
图5 基于新型的时频混合的自适应均衡算法的可见光通信系统结构图

基于DCO-OFDM调制的可见光通信系统自适应后失真技术结构如图4所示。

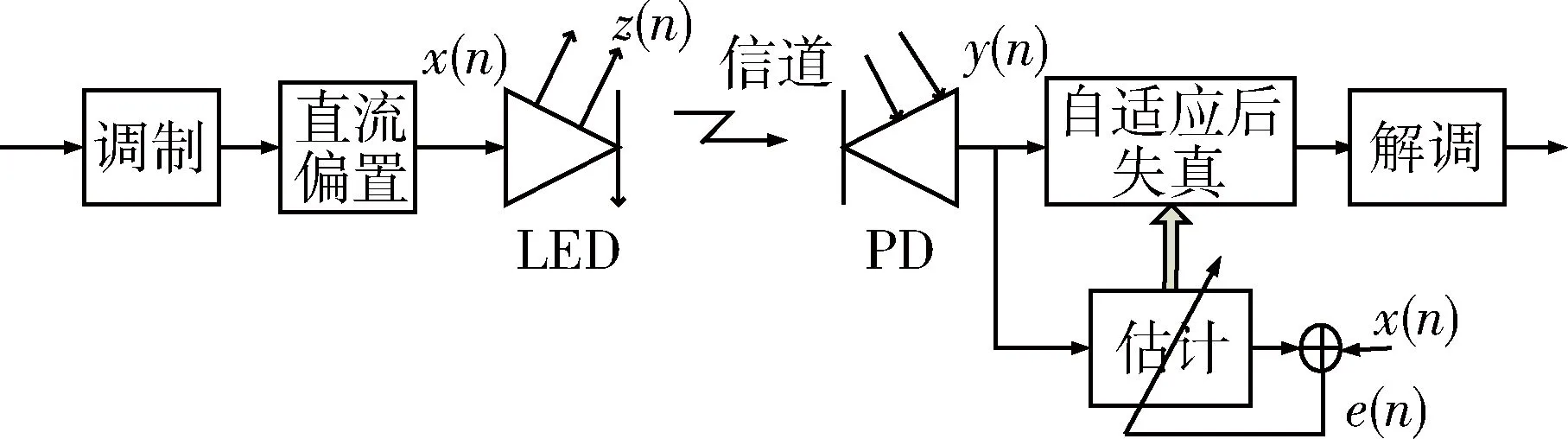
图4 基于DCO-OFDM调制的可见光通信系统自适应后失真技术结构图

多项式模型的数学表达式如下：

(7)

其中K为模型的阶数，D为最大的时延，αk,d是模型的参数。

用矢量方法表示α和y,则式(7)可以改写为：

(8)

噪声信号可以表示为：

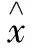
(9)

通过最小化噪声信号功率，可以得到其最小平方解：

α=(YHY)-1YHx

(10)

通过式(10)可以看出，在模型参数计算的过程中，需要对YHY求逆，直接对矩阵进行求逆对处理器的要求很高。因此，在实际操作仿真的过程中，可以采用一些实时的处理算法来递推出最小二乘解：

(11)

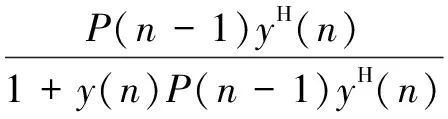
(12)

其中P(n)是YHY的转置，P(n)的初始值P(-1)定义为λ-1I,λ为任意小的常数。α(-1)的值一般取[1,0,…,0]T，以保证后失真器的增益为1。通过这种方法解出的α(n)即为所求的polynomial模型的参数。

文献[3]的仿真实验表明，采用polynomial模型作为后失真器可以很大程度上改善系统的BER和EVM性能，随着记忆多项式模型的级数的增加，BER和EVM的性能随之增加，但随着级数增加到一定的程度的时候效果不再随之增加。采用polynomial模型作为后失真器的优点在于模型结构简单，参数较少，而且效果很明显。

1.3频域均衡后失真补偿

文献[5]从频域的角度采用频域均衡的方法补偿了由于LED的非平坦频域响应造成的记忆性问题。其中，作者提出了一种新的时频混合的自适应均衡算法，这种算法基于频域均衡和判决引导最小均方算法。这种新型均衡器的结构图如图5所示。

文章在进行算法验证的过程中使用的是RBG LED作为发送器，在接收端使用的是雪崩二极管作为接收器。输入信号经512QAM调制后进行时域-频域变换，并进行预均衡，然后在信号的前面加上循环前缀，这是为了防止信号出现多径干扰。低通滤波器被用来移除带外信号，随后将信号经电子放大器放大，并加上偏置，使得信号全部为实的正值，随后通过LED转换为光信号发送出去。在接收端，去除循环前缀之后，就是一个将频域均衡和DD-LMS相结合的新型的时域-频域的均衡算法。首先，非平坦频域响应被迫零均衡所补偿，然后一旦误码率下降到10-1到10-2这样的数量级，就进行DD-LMS。DD-LMS的结构图如图6所示。

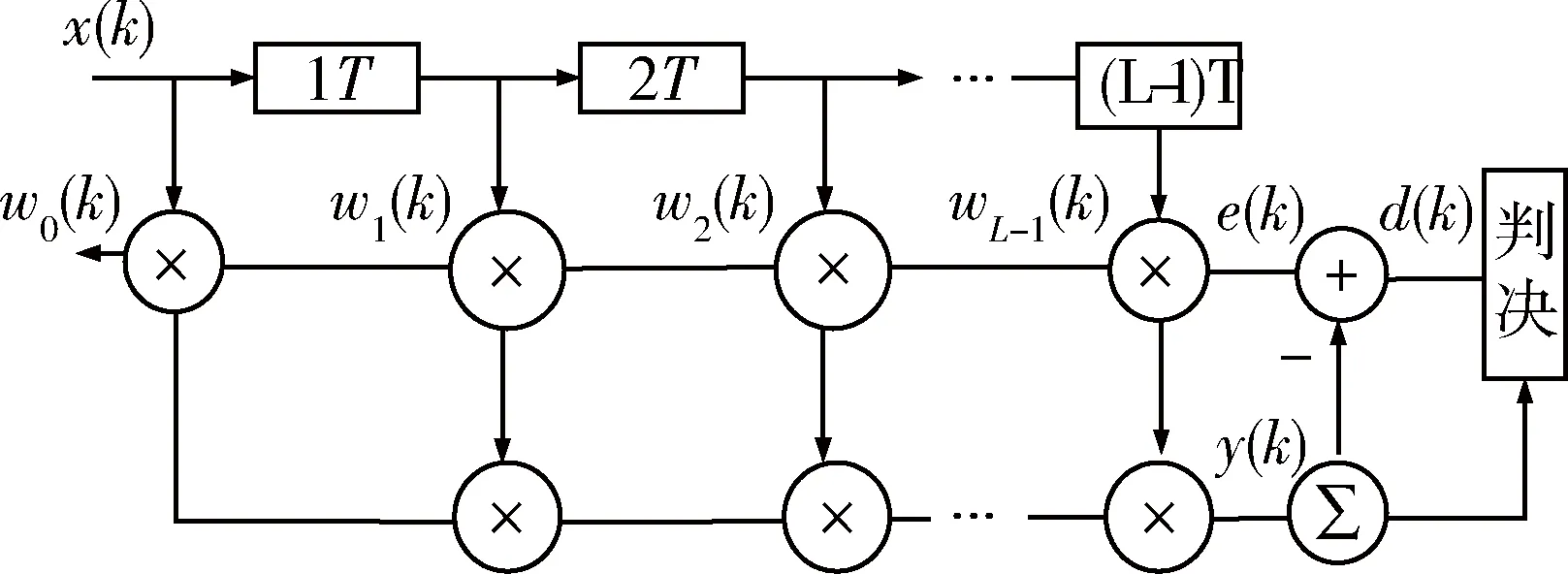
图6 DD-LMS均衡器的框架结构图

L阶DD-LMS均衡器的输出y(k)可以表示如下：

y(k)=wH(k)X(k)

(13)

w(k)=[w0(k),w1(k),…,wL(k)]T

(14)

X(k)=[x(k),x(k-1),x(k-2),…,x(k-L+1)]T

(15)

其中X(k)和w(k)表示输入信号和权重系数，误差信号和自适应更新的权重如下：

e(k)=d(k)-y(k)

(16)

w(k+1)=w(k)+μe*(k)X(k)

(17)

其中d(k)为期望的输出，μ为步长，e*(k)表示e(k)的复共轭矩阵，

使用这种新型的时域-频域混合的均衡算法，可以使数据的速率达到4.22 Gb/s。该算法虽然在发送端也对信号做了一定的预处理，但主要实现是在接收端，而且该算法是针对由于LED的非平坦响应造成的记忆性问题，但记忆性问题是LED非线性失真不可以回避的问题，因此该方法也可以认为是一种后失真补偿算法。与QIAN H的方法相比，该方法从频域的角度给出了补偿记忆性的方法，但该方法结构稍显复杂。

2 机器学习与后失真技术

机器学习是人工智能的核心，是使计算机智能化的根本途径，其研究的核心问题是如何通过计算的手段，利用经验来改善系统自身的性能。在计算机系统中，“经验”通常以“数据”形式存在，因此，机器学习所研究的主要内容是关于在计算机上从数据中产生“模型”的算法，即学习算法。下文中，将机器学习中的BP神经网络[6]和支持向量机[7]应用到后失真模块中，以这两种方法对LED的非线性特性进行后失真补偿。

2.1BP神经网络后失真补偿方法

人工神经网络是对人脑或自然神经网络的若干抽象和模拟进行分布式并行信息处理的数学模型，它具有非线性适应性信息处理能力，因此可以利用人工神经网络来拟合LED的反向特性曲线，从而对LED的非线性特性进行一定的补偿。其中BP(Error Back-propagation Algorithm)神经网络[6]是一种最常见的前向反馈神经网络，其网络拓扑结构如图7所示。

图7 BP神经网络拓扑结构图

图8 经BP神经网络补偿与未补偿星座图

人工神经网络分为三层结构：输入层、隐藏层、输出层。假设BP神经网络的输入矢量为x∈Rn,其中x=(x0,x1,…,xn-1)T；隐藏层有L个神经元，则每个神经元的输出z∈RL，z=(z0,z1,…,zL-1)T；输出层有m个神经元，则输出y∈Rm,y=(y0,y1,…,ym-1)T。输出层至隐藏层的权值为Wij,阈值为θj；隐藏层至输出层之间的权值为Wjk，阈值为θk。则各层的输出可以表示为：

(18)

其中激活函数f(x)可以根据需要选取单极性Sigmoid函数或双极性Sigmoid函数。

BP神经网络的学习，即为BP神经网络的各层权值和阈值的学习，其学习过程是由信号的正向传播与误差的反向传播两个过程组成。在拟合可见光通信系统LED非线性特性曲线的反向特性的时候，可以将接收器接收到的信号作为神经网络的输入x(n)，将经过Wiener模型之前的信号作为神经网络的输出y(n)来训练网络，从而得到神经网络的权值和阈值。

BP神经网络的学习规则是基于最小均方误差准则。当一个样本(设为第p个样本)输入网络，并产生输出时，均方误差应为各输出单元误差平方和，即：

(19)

当所有的训练样本输入一次后，总误差为：

(20)

设wsp为网络中的一个连接权值，则根据梯度下降法，批处理方式下的权值修正量应为：

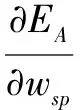
(21)

所以，在批处理条件下，对于输出层的权值调整为：

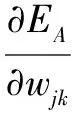
(22)

对于中间隐藏层的权值调整为：

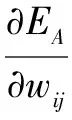
(23)

在实验仿真的过程中，以Wiener模型模拟LED的非线性特性对系统造成的影响，采用16QAM调制对输入信号进行调制，128点的快速傅里叶变换，使用DCO-OFDM对发送信号进行调制，减小LED的记忆性带来发符号间干扰，训练数据有128 000组。通过实验仿真，发现BP神经网络可以很好地对LED的非线性进行补偿。未经BP神经网络补偿与经过神经网络补偿之后的星座图如图8所示，信噪比与误码率的关系曲线如图9所示。

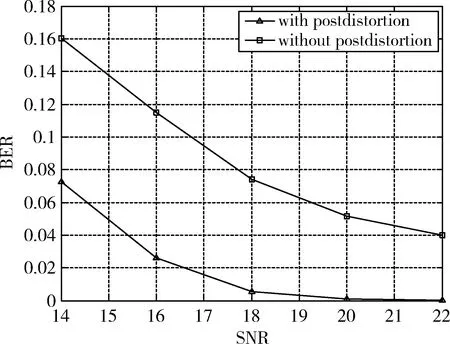
图9 误码率与信噪比的关系曲线

BP神经网络与polynomial模型相比，虽然模型结构相对大一点，而且参数较polynomial多，但效果和polynomial模型很相近，并且神经网络作为机器学习领域中的一个部分，是以后大数据时代的主流方法，相比于一般的数学模型，会显得更加智能化。

2.2支持向量机后失真补偿方法

SVM算法最初是为了解决二分类问题而设计的，其主要思想是建立一个分类超平面作为决策曲面，使得正例和反例之间的隔离边缘被最大化，从而实现最优分类问题。由于其使用结构风险最小化原则，在损失函数的基础上引入调节项，同时折中考虑经验风险和函数的复杂度，使得实际风险最小，从而有效地避免了传统的神经网络会出现过拟合的问题。

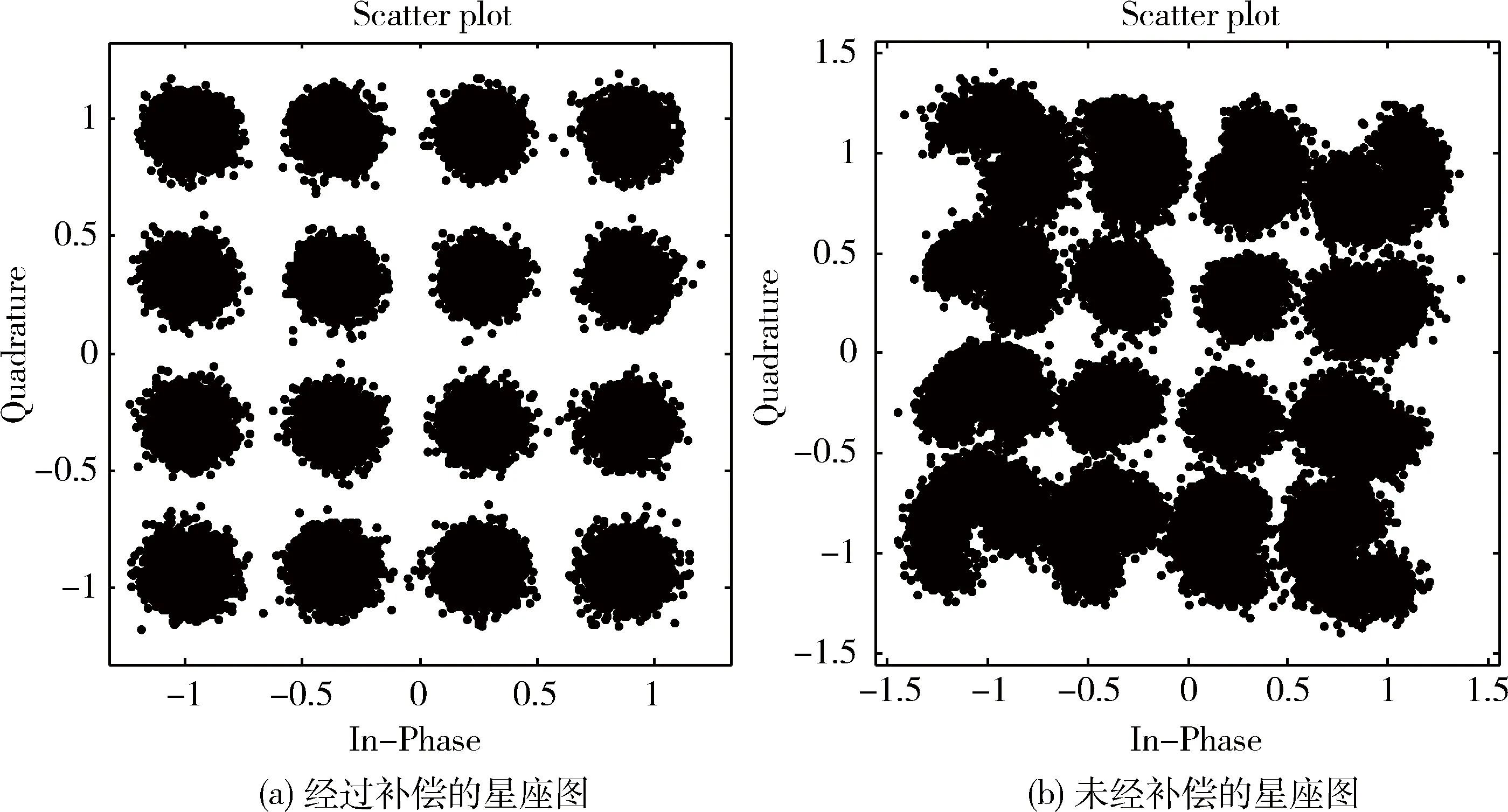
图11 经支持向量机补偿与未补偿星座图

图10所示为支持向量机体系结构图，其中K为核函数，其主要类型有：线性核函数、多项式核函数、径向基核函数以及两层感知器核函数。以最常见的二分类支持向量机模型C-SVC为例，其具体形式如下：

(1)设已知训练集：

T={(x1,y1),…,(xl,yl)}∈(X×Y)l

(24)

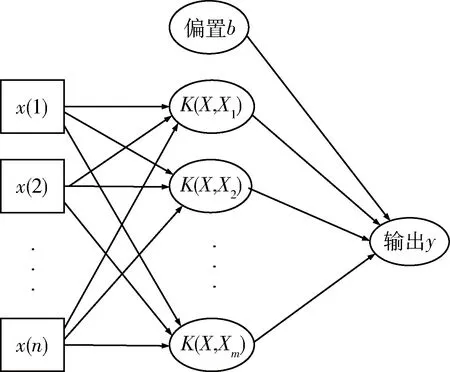
图10 支持向量机体系结构图

其中，xi∈X=Rn，yi∈Y={1,-1}(i=1,2,…,l)；xi为特征向量。

(2)选取适当的核函数K和适当的参数C，构造并求解最优化问题：

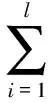
(25)

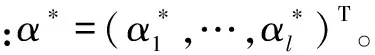
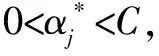
(26)

(4)构造决策函数：

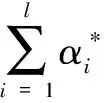
(27)

对支持向量机同样进行了实验仿真，其系统仿真参数设置和BP神经网络中相同，训练数据也相同，结果显示支持向量机作为后失真模块，对LED的非线性特性进行补偿同样具有比较好的效果。经过支持向量机补偿之后的星座图和未经补偿的星座图如图11所示，信噪比与误码率的关系曲线如图12所示。

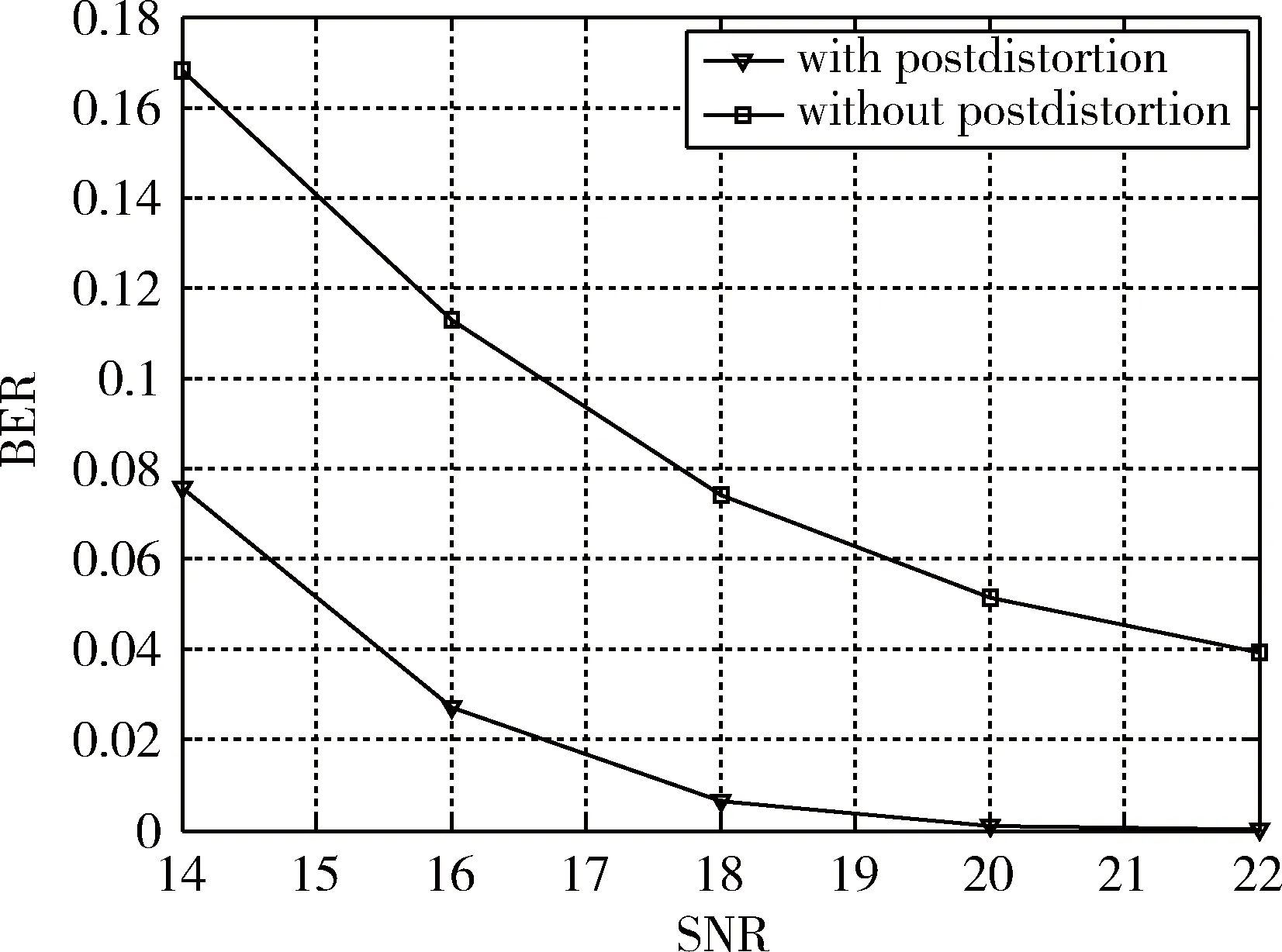
图12 误码率与信噪比的关系曲线

3 结论

随着白光LED的普及，可见光通信作为新型的光无线通信技术，拥有着巨大的发展机遇的同时，也面临着LED的记忆性非线性问题对通信系统性能的挑战。本文总结了3种现有的后失真补偿方法：Volterra判决反馈均衡、自适应后失真补偿以及频域均衡，通过后失真补偿技术降低LED的非线性对通信系统造成的影响。其中Volterra判决反馈均衡和频域均衡方法相比于自适应后失真补偿方法，其结构相对较为复杂，且算法复杂度相对较高，而且频域均衡的方法仅仅研究了LED的记忆性问题。在以上基础上，提出了将后失真技术与机器学习的方法相结合，作为人工智能的核心技术，机器学习方法中的BP神经网络和支持向量机同样可以在接收端对LED的非线性特性进行补偿。

[1] Ying Kai, Yu Zhenhua, BAXLEY R J, et al. Nonlinear distortion mitigation in visible light communications[J]. IEEE Wireless Communications, 2015, 22(2): 36-45.

[2] STEPNIAK G, SIUZDAK J, ZWIERKO P. Compensation of a VLC phosphorescent white LED nonlinearity by means of volterra DFE[J]. IEEE Photonics Technology Letters, 2013,25(16): 1597-1600.

[3] KAMALAKIS T, WALEWSKI J W, NTOGARI G, et al. Empirical volterra-series modeling of commercial light-emitting diodes[J]. Journal of Lightwave Technology, 2011, 29(14): 2146-2155.

[4] QIAN H, YAO S J, CAI S Z, et al. Adaptive postdistortion for nonlinear LEDs in visible light communications[J]. IEEE Photonics Journal, 2014, 6(4): 1-8.

[5] WANG Y, HUANG Y, ZHANG J, et al. Enhanced performance of visible light communication employing 512-QAM N-SC-FDE and DD-LMS[J]. Optics Express, 2014,22(13): 15328-15334.

[6] 盛仲飙. BP神经网络原理及MATLAB仿真[J]. 渭南师范学院学报,2008,23(5):65-67.

[7] SEBALD D J, BUCKLEW J A. Support vector machine techniques for nonlinear equalization[J]. IEEE Transactions on Signal Processing, 2000,48(11): 3217-3226.

2017-04-20)

徐旭东(1993-)，男，硕士研究生，主要研究方向：可见光通信，机器学习。

Nonlinear post-distortion for LED in visible light communication

Xu Xudong

(College of Telecommunications and Information Engineering, Nanjing University of Posts and Telecommunications, Nanjing 210003, China)

In a visible light communication system, the light emitting diode(LED) is the major source of nonlinearity. The research on compensation technique for LED nonlinear distortion is divided into predistortion and post-distortion. Predistortion may not be a cost-efficient approach as it needs additional feedback circuits at the transmitter. Compared to predistortion, post-distortion compensates the signal at the receiver and does not require an additional feedback loop. The existing post-distortion methods, such as the Volterra decision feedback equalizer(DFE),the adaptive post-distortion and the frequency domain equalization, have greatly mitigated the nonlinear distortion of LED. Machine learning as the core of intelligence, combined with post-distortion, also can mitigate the impact of nonlinear distortion of LED.

post-distortion; Volterra DFE;adaptive post-distortion; frequency domain equalization; machine learning

TN92

A

10.19358/j.issn.1674- 7720.2017.22.021

徐旭东.可见光通信中LED的非线性后失真补偿技术研究J.微型机与应用，2017,36(22)：78-82,90.

国家自然科学基金(61603197)；江苏省博士后基金(1401045C)；南京邮电大学科研基金(NY214034,NY215104)