群体平衡模型在气液搅拌数值模拟的研究进展

王文鹏，周三平

（西安石油大学机械工程学院，陕西西安 710065）

专论与综述

群体平衡模型在气液搅拌数值模拟的研究进展

王文鹏，周三平

（西安石油大学机械工程学院，陕西西安 710065）

气液搅拌反应釜在过程工业中应用广泛，在气液的分散和混合过程中，准确模拟预测离散相系统中气泡大小与分布在流体力学和传质中起着关键性作用。群体平衡模型（Population Balance Model，PBM）是描述两相以及多相流体系中分散相的尺寸大小及分布程度随时间和空间变化的通用方程模型，可以较准确的预测釜内流场和气泡的大小与分布。对群体平衡模型在气液搅拌数值模拟中的应用进行了综述，讨论了PBM的数学模型和主要的数值求解方法，然后着重介绍了近年来采用PBM对气液搅拌数值模拟的情况，进行了总结和展望。

气液搅拌；群体平衡模型；气泡尺寸；数值模拟

搅拌与混合是应用最为广泛的过程操作之一，同时搅拌反应釜大量应用于化工、轻工、医药、食品、生物发酵及废水处理等行业中。其中，气液搅拌反应釜应用较为广泛。在气液的分散和混合过程中，液相中的气泡大小与分布在流体力学和传质中起着重要作用，在实际工况下，它决定着气泡的上升速度和气体在液相中的停留时间，影响着液相中的气含率及气液的接触面积[1]。群体平衡方程（Population Balance Equation，PBE）是描述两相以及多相流体系中分散相的尺寸大小及分布程度随时间和空间变化的通用方程，能够具体地描述离散相实体的分布情况和影响分布变化的离散相微观活动。由此创建了群体平衡模型（Population Balance Model，PBM），形成了一种通用方法。最初由Hulburt＆Katz[2]于1964年在化工过程中使用。近年来随着计算机科学的快速发展，以及对PBE求解方法的深入研究，将PBM应用于越来越多的化工过程中，尤其是在气液搅拌过程中，获得了气相在液相中，气泡的直径大小和气泡的分布情况。同时，计算流体力学（Computional Fluid Dynamics，CFD）技术的发展与完善，在多相流领域越来越受到关注。将CFD对流场预测能力强与适应范围广的特点和PBM计算气体颗粒大小与分布的优点相结合，利用CFD-PBM耦合模型，应用于气液搅拌反应釜中，可以得到与实验更加一致的数值模拟结果，有利于更加深入地了解搅拌过程中的多相流动和传递规律，为搅拌反应釜的优化设计、操作和放大提供理论指导。本文对群体平衡模型在气液搅拌反应釜数值模拟中的应用情况进行综述，同时包括其基本模型方程和主要的求解方法以及其中的聚并、破碎模型，最后对群体平衡模型在气液搅拌中的应用进行总结和展望。

1 模型与数值求解方法

1.1 数学模型

PBE是描述多相流体系中颗粒状态分布随时间与空间连续变化的偏微分方程[3]。其中，粒子状态矢量是通过一系列的外部坐标x→以及内部坐标来定义的，外部坐标代表粒子的空间位置，内部坐标则包含粒子的大小、温度、组成等相关量。

局部平均粒子数量密度为（即每单位体积的粒子总数）：

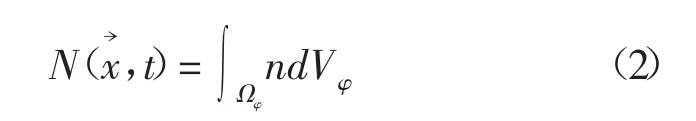
所有粒子的总体积分数为：

其中：V（φ）-粒子在状态空间φ中的体积。

因此群体平衡方程的表示，假定φ为粒子体积，数量密度函数的传递方程为：

其边界条件以及初始条件为：

1.2 数值求解方法

1.2.1 聚并与破碎 在粒子聚并和破碎过程中往往伴随着新粒子的生成和死亡。其中，在气-液搅拌体系中，气泡之间发生聚并现象的前提是气泡间可以进行相互碰撞，液相的湍动作用和气泡自身所具有的浮力作用使气泡获得不同的瞬时运动速度，使得气泡在不同瞬时运动速度的条件下发生碰撞，从而一部分发生相互碰撞的气泡产生聚并现象[5]。

目前，研究气泡的聚并过程均指的是两两气泡之间聚并的过程，气泡聚并过程主要为两气泡发生接触、碰撞，随之形成薄厚不一的液膜，当液膜足够稀薄，超越临界厚度时，液膜破裂完成聚并。气泡聚并速率等于气泡碰撞频率乘以聚并效率。气泡聚并过程示意图（见图 1）。

图1 气泡聚并过程示意图[5]

聚并核的单位是m3/s，其通常由两个部分组成：聚并频率：体积为V、V′的粒子的碰撞频率；

聚并有效性：体积为V、V′的粒子发生聚并的可能性。

则，聚并导致的粒子产生项为：

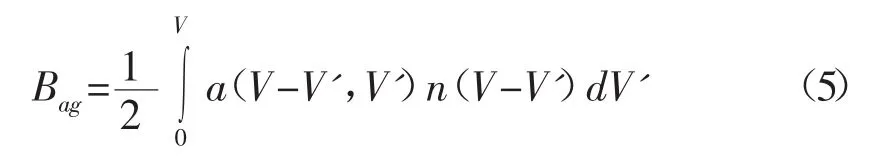
其表示体积为V-V'的粒子和体积为V的粒子聚并后生成体积为V的新粒子。1/2用来防止对一次聚并进行重复计算。

体积为V的粒子聚并死亡项为：

气泡液膜破裂是由于气泡薄膜的不稳定性造成的，液膜的稳定性会受到分子间范德华作用力引起的界面临界波长所产生的放大效应的影响，从而引起气泡的破碎。气泡破碎机制有：湍流涡体碰撞，液体流场剪切以及大气泡表面不稳定性等几种。在搅拌气液体系中，气泡破碎主要是由湍流涡体碰撞引起的（见图2）。

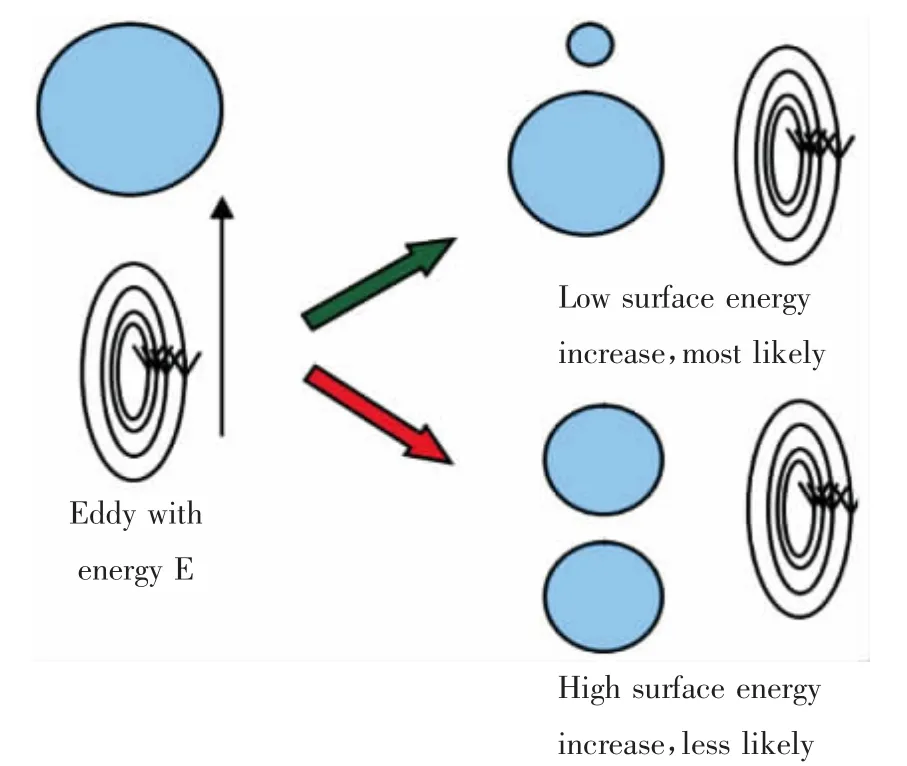
图2 气泡破碎过程示意图[5]

用下面的表达式来表达破碎核：

其中：g（V'）-破碎频率，即为体积为 V'的粒子破碎所用时间的倒数；β（V│V'）-概率分布密度函数（DSD），即为粒子从V'体积破碎为V的可能性。

破碎导致的粒子生成这样来表示：

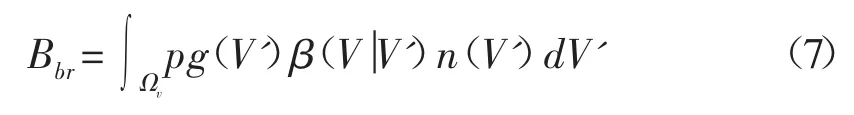
其物理意义为每单位时间有体积为 V'，g（V'）n（V'）dV'数量的粒子破碎并产生 pg（V'）n（V'）dV'数量的新粒子。p为新破碎产生的子粒子数量，例如如果破碎产生2个粒子，那么p即为2。

破碎导致体积为V的粒子的死亡这样来表示：

1.2.2 求解方法

1.2.2.1 均一离散法 均一离散法是由Hounslow等[6]，Kumar＆Ramkrishna[7]提出。它将连续的粒子数量密度函数使用一系列离散的bins来表示，在均一离散法中，颗粒群的粒径范围被离散为有限的粒径间隔。这种方法的优点在于可以直接计算粒径分布。如果在求解前，粒径分布就已经可以大体的进行预估且数值的波动处于2～3倍的时候，均一离散法非常有效。在这种情况下，颗粒群被离散为相对小的粒径间隔并和计算流体动力学（CFD）耦合求解。这个方法的缺点就是如果需要很大数量的粒径间隔，占用计算资源较多。

1.2.2.2 非均一离散法 均一离散法的一个限制就是所有bins依附于第二相，因此其动量和与第二相的动量相同。实际上，在某些情况下，一些过大的以及过小的粒子会由于动量的偏差引起分离，均一离散法并不适用于这些情况。非均一离散法有效的处理了这个问题。在非均一离散法中，bins群可以调用不同的相速度，因此如果非均一离散法激活，群体平衡模型可以应用于多个离散相的体系。

1.2.2.3 标准矩方法 求解群体平衡模型的另一个方法是标准矩方法（SMM）[2]。在标准矩方法中，群体平衡方程被转换成为一系列的矩方程。第i个矩被定义为在整个粒径空间内，将数量密度函数乘以粒径的i次幂的函数的积分。一般情况下，求解少数几个矩方程就够了，通常是3到6个。和离散法相比，矩方法求解的方程数量大大减少。除了在计算速度上的优点，如果不需要连续的数量密度函数，且用几个节点值就足够近似的表示数量密度函数的话，SMM方法非常有效。通常，零阶矩表示总数量密度、二阶矩表示每单位体积的粒子表面积、三阶矩表示总质量密度。

1.2.2.4 积分矩方法 积分矩方法（QMOM）[8]在计算速度上和SMM具有相同的优势，不同的是，QMOM使用积分来封闭方程组（这在SMM中是通过用矩本身来封闭）。这使得QMOM可以更加广泛的应用。

2 PBM在气液搅拌数值模拟的应用

化学化工领域，气液搅拌反应釜广泛的应用于生物发酵、医药食品和工业的废水处理等过程中。在气液搅拌的混合和分散过程中，气泡的尺寸大小和分布在气液的传质中都起着重要的作用，它决定着气泡的上升速度和气体在液相中的停留时间，控制着含气率以及气液接触的面积。

Bakker等[9]是最早将PBE用于模拟气液搅拌混合过程，如今已在搅拌反应釜内考虑分散相颗粒微观行为时多相流体系的模拟中取得广泛应用，尤其今年不少研究者应用PBM模拟了搅拌反应釜中的气液多相体系。

Laakkonen等[10]分别对六直叶涡轮搅拌桨和单层6-RT搅拌桨气液搅拌釜内气泡尺寸分布通过商业软件CFX5.7进行了数值模拟。PBM模型采用的是Lehr模型，该模型已成功地对鼓泡塔内气泡尺寸激情分布进行了模拟预测，通过UDF编译加入到软件中，其中的一些参数根据实验数据确定，对搅拌反应釜内气泡的尺寸以及分布进行了很好的预测。

Kerdouss等[11]使用商业软件FLUENT，对双层六直叶涡轮桨搅拌釜内流场进行了数值模拟，采用Euler-Euler双流体模型、修正的曳力系数模型以及考虑气泡的聚并与破碎模型，并取得较为理想的结果。所得的釜内气液流场呈现典型的桨叶上下双循环流型，观测到气含率分布较为合理，同时可以观察到桨叶及挡板后有大量气泡聚集，产生气穴现象，整体气泡尺寸及分布与实验值较为吻合，但是桨叶附近的气含率与实验值偏差较大，可能原因是PBM不够完善，模拟存在误差。

Martin等[13]利用PBE以及通过在聚并、破碎过程中考虑液体黏性的影响，模拟了在搅拌反应釜中液体黏性对气泡大小分布和气液传质速率的影响。通过分析，得到模拟结果与实验结果基本一致，随着液体黏度的增大使得气泡的平均直径略有增大，同时得到气泡平均直径和气液传质系数的关系与实验值基本保持一致（见图 3）。

Selma等[12]采用CFD-PBM耦合模型对鼓泡塔和搅拌反应釜内气液混合进行了数值模拟，得到了其气含率以及气泡尺寸的模拟结果，并比较了DQMOM和CM两种PBM求解方法对模拟结果的影响，最终得到的结果表明：两种求解方法均能很好地模拟预测鼓泡塔和搅拌反应釜内气含率和气泡尺寸大小的分布，但DQMOM方法更加节约计算资源，计算效率更高。

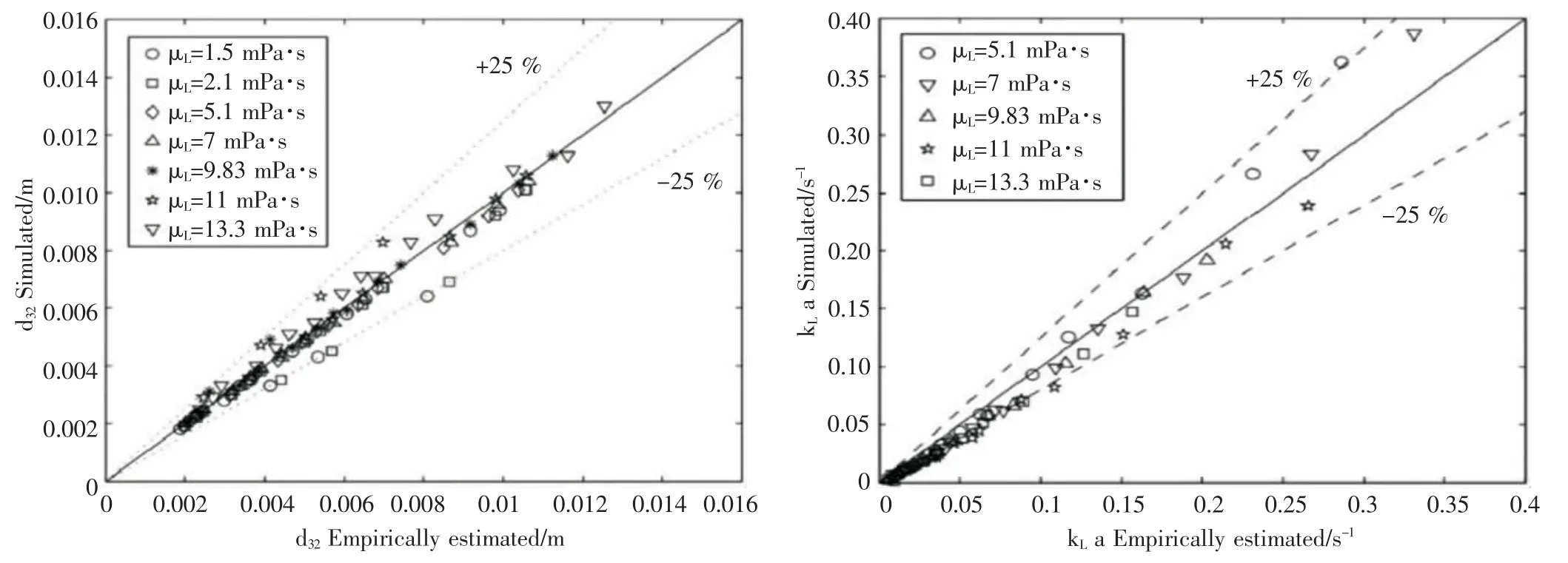
图3 模拟得到的平均气泡直径和体积传质系数与实验数据的对比

杨锋苓等[14]通过商业软件FLUENT，采用Euler-Euler双流体模型，假设气泡为球形，利用PBM模型模拟气泡的聚并与破碎过程，对标准CD-6桨搅拌釜内流场进行数值模拟，研究其气液混合性能。通过模拟结果，分析了不同转速和通气量时搅拌釜内流场、气含率和搅拌功耗，并与实验数据进行对比，基本保持一致，验证了所建模型和模拟方法的可靠性；同时验证了一种新型错位CD-6桨，与标准CD-6桨相比，相同工况下，错位桨湍动程度高，气泡分布均匀，搅拌功耗略低，更适用于气液混合搅拌。

3 结语

气液搅拌反应釜广泛的应用于石油、化工、食品医药及污水处理等工业过程中，其内部为气液多相流体系，其中气体的平均粒径和分布对于过程控制、传质和传热都是十分重要的影响因素[15]。因此，将群体平衡模型（PBM）应用于气液搅拌反应釜内的多相流的模拟，获得气泡的粒径尺寸和分布情况，对于研究气液搅拌混合及其传质传热都有着重要的意义。

近年来利用PBM模拟气液搅拌混合体系已经得到了许多应用。在气液混合体系中，气泡的聚并和破碎过程一般不能忽略，PBM正好满足了这些条件，PBM多用离散方法进行数值求解，随着进一步研究，近年来也有学者利用积分矩方法求解。从整体的模拟结果上来看，大多数的结果与实验结果进行比较，大致吻合，也更好的印证了PBM可以用来描述气液搅拌混合过程中气泡的大小及其分布，并且一些学者计算了气液传质系数，可以对时间作用进行更为合理的表征。但在目前的研究过程中关于PBM的应用存在的一些问题，首先在模拟过程中采用PBM处理气泡的分布计算量比较大，占用计算资源较多；其次是气泡的聚并、破碎模型直接影响着模拟质量，由于气体物性比较复杂，同时聚并、破碎模型尚不完善，其中存在许多不确定的可调参数，模拟出的结果会产生一定的误差。所以就需要继续对气泡的聚并及破碎模型进行深入的研究，完善群体平衡模型。相信随着对气液混合体系研究的深入以及新的气泡聚并、破碎模型的研发，PBM对于描述气液多相流体系中的气泡的大小及分布会更为全面和准确，从而研究出更加高效的气液搅拌反应釜。

［1］包雨云，高正明，施力田.多相流搅拌反应器研究进展［J］.化工进展，2005，24（10）：1124-1130.

［2］Hulburt H M，Katz S.Some problems in particle technology：A statistical mechanical formulation［J］.Chemical Engineering Science，1964，19（8）：555-574.

［3］Randolph A D，Larson M A.Theory of particulate processes［M］.2nded.San Diggo，CA：Academic Press，1988.

［4］苏伟军，顾兆林，XU X.Yun.离散相系统群体平衡模型的求解算法［J］.中国科学：化学，2010，40（2）：144-160.

［5］Chen P，Sanyal J，Dudukovic M P.Numerical simulation of bubble flows：effect of different breakup and coalescence closures ［J］.Chemical Engineering Science，2005，60（4）：1058-1101.

［6］Hounslow MJ，Ryall RL，Marshall VR.A discretized population balancefornucleation.Growth，and aggregation［J］.AIChE J，1988，34（11）：1821-1832.

［7］Kumar S，Ramkrishna D.On the solution of population balance equations by discretization ［J］.Chemical Engineering Science，1996，51（8）：1311-1342.

［8］McGraw R.Description of aerosol dynamics by the quadrature method of moments ［J］.Aerosol Science and Technology，1997，27（2）：255-265.

［9］Bakker A，Akker H E A.A computational model for the gasliquid flow in stirred reactors ［J］.Chem.Eng.Res.Des.，1994，72：594-606.

［10］Laakkonen M，Moilanen P，Alopaeus V,et al.Modeling local bubble size distribution in agitated vessels［J］.Chemical Engineering Science，2007，62（3）：721-740.

［11］Kerdouss F，Bannari A，Proulx P，et al.Two-phase mass transfer coefficient prediction in stirred vessel with a CFD model ［J］.Computers ＆ Chemical Engineering，2008，32（8）：1943-1955.

［12］Selma B，Bannari R，Proulx P.Simulation of bubbly flows：Comparison between direct quadrature method of moments（DQMOM）and method of classes（CM）［J］.Chemical Engineering Science，2010，65（6）：1925-1941.

［13］Martin M，Montes F，Galan M A.Mass transfer rates from bubbles in stirred tanks operating with viscous fluids［J］.Chemical Engineering Science，2010，65（12）：3814-3824.

［14］杨锋苓，周慎杰.双层错位CD-6桨搅拌槽内的气液混合性能［J］.华中科技大学学报（自然科学版），2015，43（11）：16-21.

［15］王铁峰.气液态反应器流体力学行为的实验研究与数值模拟［D］.北京：清华大学博士学位论文，2004.

Research progress of population balance model in numerical simulation of gas-liquid mixing

WANG Wenpeng，ZHOU Sanping
（College of Mechanical Engineering，Xi'an Shiyou University，Xi'an Shanxi 710065，China）

The gas-liquid stirred tank reactors is widely used in process industry.During the gas-liquid dispersion and mixing process,accurate simulation and prediction of bubble size and distribution in discrete phase systems plays a key role in fluid mechanics and ass transfer.Population Balance Model（PBM）is a universal equation model describing the size and distribution of dispersed phase which changes with time and place in two-phase and multiple fluid systems.It can predict the flow field and the size and distribution of bubbles accurately.This article summarizes the application of population balance model in numerical simulation of gas-liquid mixing,discusses the mathematical model of PBM and the main numerical solution methods,then mainly introduces,summarizes and looks forward to the prospects of the application of PBM in numerical simulation of gas-liquid mixing in recent years.

gas-liquid mixing；population balance model；bubble size；numerical simulation

TQ051.7

A

1673-5285（2017）11-0001-05

10.3969/j.issn.1673-5285.2017.11.001

2017-10-23

王文鹏，男（1991-），陕西省铜川市人，硕士，研究方向为化工过程机械，邮箱：wangwp_ryan@163.com。