基于改进SVPWM的多电平风电并网逆变器的研究

李 沁,李绍武,廖红华,艾 青,高仕红

(湖北民族学院 信息工程学院,湖北 恩施 445000)

基于改进SVPWM的多电平风电并网逆变器的研究

李 沁,李绍武,廖红华,艾 青,高仕红

(湖北民族学院 信息工程学院,湖北 恩施 445000)

针对风电系统中中点箝位式多电平并网逆变器存在的传统空间矢量调制方法(SVPWM)计算繁琐和中点电压不稳定的问题,在120°坐标系下,将传统SVPWM中大量的三角函数和求根运算用线性运算代替,通过简化SVPWM算法,减小运算量、提高运行效率;通过直流侧中点电压偏差调节矢量运行时间,实现直流侧中点电压平衡控制,减小谐波含量;并对风电系统的逆变并网部分进行了仿真,结果验证了该SVPWM调制方法的可行性和有效性,为实际中实现具有较高电能质量的风电并网提供了研究基础.

空间矢量脉宽调制;多电平逆变器;线性运算;中点电位;风电并网

随着新能源技术的不断发展,风电装机容量在电力系统中比重越来越大,大功率的风电变流器已经成为研究和应用的热点.在高压大功率领域中,多电平换流器以其具有开关管承受电压应力小、输出电压谐波含量少的优点得到了广泛的应用,具有良好的发展前景[1],因此在风力发电系统中三相PWM逆变器也是研究热点,其并网过程受到广泛关注[2].

变速恒频风力发电系统中,核心是连接电网的逆变器.交流侧的逆变电压需在幅值、频率、相位上满足与电网电压一致的条件才能并网,谐波电流尽可能低,功率因数可调,能向电网提供稳定的功率[3].

并网逆变器常用PWM(脉宽调制)、SPWM(正弦脉宽调制)和SVPWM(空间矢量脉宽调制),其中SVPWM调制方法的电压利用率高、输出波形谐波含量较小、动态响应快、容易数字实现,因而应用非常广泛.传统的SVPWM方法中,运算包含大量的三角函数和求根运算,而在120°坐标系下可以大大简化各个扇区基本矢量的作用时间的计算[4],通过对比分析SPWM与SVPWM可知,在两电平SPWM输出中加入特定的零序分量可以得到SVPWM的数学本质[5],采用一种改进的SVPWM形成多电平并网逆变器的输出波形,该方法通过推导在120°坐标系下各相调制波与占空比的表达式,其表达式省去了传统SVPWM中繁杂的三角函数和求根计算,只含有线性计算,节约运算资源和时间,通过电压矢量角度的不同灵活调整非零矢量和零矢量的顺序,使输出波形对称性更好[6];在此基础上,将一种基于中点电位偏移量的滞环控制方法引入改进的空间矢量调制方法中,可以精确控制中点电位,进一步减小谐波含量,改善并网的电能质量,实验结果证明了理论的可行性[7].

1 直驱型风电并网系统的结构

图1 永磁直驱式风力发电系统Fig.1 Direct-drive permanent magnet generator wind power system

本文研究的为永磁直驱型风力发电系统,图1为其发电系统的结构图,包括发电机、变流器.该类型的风电系统变流器直接与风机相连,容量与风机相等.其中逆变器为多电平逆变器,采用SVPWM控制,图2为其逆变器的主电路结构.

图2 多电平逆变器拓扑结构Fig.2 Topology of a three-level inverter

2 改进SVPWM原理分析

实现该SVPWM调制方法的步骤为：①考矢量位置以及由哪三个矢量合成；②本电压矢量的作用时间；③优化输出矢量开关顺序,调节中点电位平衡.

2.1开关状态分析

对于图2所示的多电平逆变电路,根据三相对称原理,以A相为例,输出电压为ua=Udc/2,定义为P状态,输出电压为ua=0,定义为O状态,输出电压为ua=-Udc/2,定义为N状态.输出电压矢量为:

图3 电压空间矢量分布图Fig.3 Voltage space vector graph

对于三相多电平逆变器,每相开关状态都有3种,因此逆变器开关状态的组合共有27种[8],如图3所示.

由图3可知,27个矢量中共有3个零矢量、12个小矢量、6个中矢量、6个大矢量,3个零矢量在中点重合,12个正负小矢量分别为P型矢量和N型矢量,并互为冗余矢量,因此输出有效的空间矢量为19个,6个大矢量将空间分为6个扇区.

图4 扇区Ⅰ的矢量分布Fig.4 Vector distribution in sectorⅠ

根据SVPWM调制的对称关系,以扇区Ⅰ为例对图3所示的多电平逆变器参考矢量进行分析.根据矢量作用的时间顺序和不同的基本电压矢量,可以将扇区分为6个小三角形区域,如图4所示.

2.2空间电压矢量作用时间确定

令ua、ub和uc为三相正弦电压信号的给定值,相位依次相差120°,uab、ubc和uca为相应的线电压,PWM开关周期为Ts.根据等幅值坐标变换,在区域2.1内各基本电压矢量作用的时间可由式(2)计算:

(2)

各基本电压矢量作用的时间如图5所示:

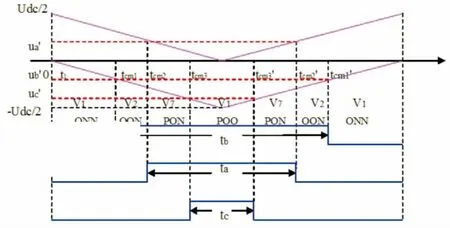
图5 扇区ⅠSVPWM时序关系Fig.5 SVPWM timing in sectorⅠ

图5中,ta、tb、tc为a、b、c三相在一个载波周期内高电平导通的时间.一个开关周期内,任意一相只会在两种状态之间变化,或者为P状态和O状态之间,或者为O状态与N状态之间,前者定义高电平为P状态,后者定义高电平为O状态.

引入控制因子k和三个中间变量,令:

(3)

结合图4和图5,当参考电压矢量落在2.1区域时,有:

(4)

可得三相调制波的表达式:

(5)

由于SVPWM的本质是在SPWM的正弦调制信号中注入零序电压[5,9-10],SVPWM的调制波可以由典型的SPWM调制波等效实现,即:

(6)

由式(2)到式(6)可得区域2.1内零序电压的表达式为:

uz=0.75(1+k)Udc+uca-1.5(1+k)uab-2ubc

(7)

同理可得扇区Ⅰ中其它区域零序电压的表达式,如表1所示:

表1 扇区Ⅰ各区域零序电压

(8)

其他区域的计算同理,在此不再赘述.

2.3中点电位平衡的控制

在多电平逆变器中,电容中点的不对称包括稳态的直流偏移和动态的低频交流分量,这种不对称会产生谐波,增大电容应力,使功率开关电压不一致甚至被击穿,不利于变流器的安全稳定运行,因此需要采用中点电位平衡控制来消除或者减小这些影响[11].由于P型小矢量和N型小矢量对于中点电位贡献效果相同,因此可以通过调节两种矢量的有效时间比例来实现中点电压平衡的控制[12].

在式(3)中,令k=ρe,其中e为中点电压的偏移量,ρ为中点电位控制因子,在满足谐波前提下合理选择ρ值可以更好的获得中点平衡控制性能,当中点电位偏低则ρegt;0,若中点电位偏高则ρelt;0,即:

(9)

通过检测直流侧两电容电压间的差值,调整两个小矢量的作用时间,形成闭环控制,使得中点电压控制在期望范围内.

3 风电并网系统的仿真分析

3.1仿真参数设置

为了验证所给出的三相多电平逆变器控制方法的有效性,以图1所示对风力发电并网系统进行仿真分析.用Matlab/Simulink软件对本文的调制方法进行仿真研究,算法基于s函数实现.相关仿真参数设置为:直流母线电压Udc=600V,直流侧等效电阻Rs=0.2Ω,稳压电容C1=C2=900 μF;交流侧滤波器电感L=9 mH,滤波器寄生电阻R=5Ω;开关周期Ts=1 ms;中点电位控制因子ρ=0.6,实现中点电位平衡滞环控制的环宽为20V;电网电压220V/50Hz.

3.2仿真结果及分析

根据图1的三相电压型逆变器的结构,以及上述参数设置,分别采用传统的SVPWM和采用中点电位平衡控制的改进型SVPWM调制方法对直驱型风电并网逆变器进行了仿真分析.由于运算减少了三角函数和求根计算,仿真过程改进SVPWM调制过程所用时间少于传统SVPWM调制.采用etime函数进行仿真计时,传统SVPWM的仿真过程需要64.237 s,而将三角函数和求根计算改进为线性计算后的改进SVPWM则只需要31.845 s,减小了仿真运行的时间,提高了程序运行效率.

图6 直流侧中点电位波形Fig.6 The waveform of DC-link neutral point vlotage

风电系统多电平逆变器并网模型仿真运行,模型中为七电平并网逆变器,仿真结果如下:图6为直流侧电容中点电位波形图;图7为引入中点电位平衡控制的改进SVPWM调制法逆变器线电压与线电压基波波形；图8为传统SVPWM算法与改进SVPWM算法调制波输出的谐波分析对比图.

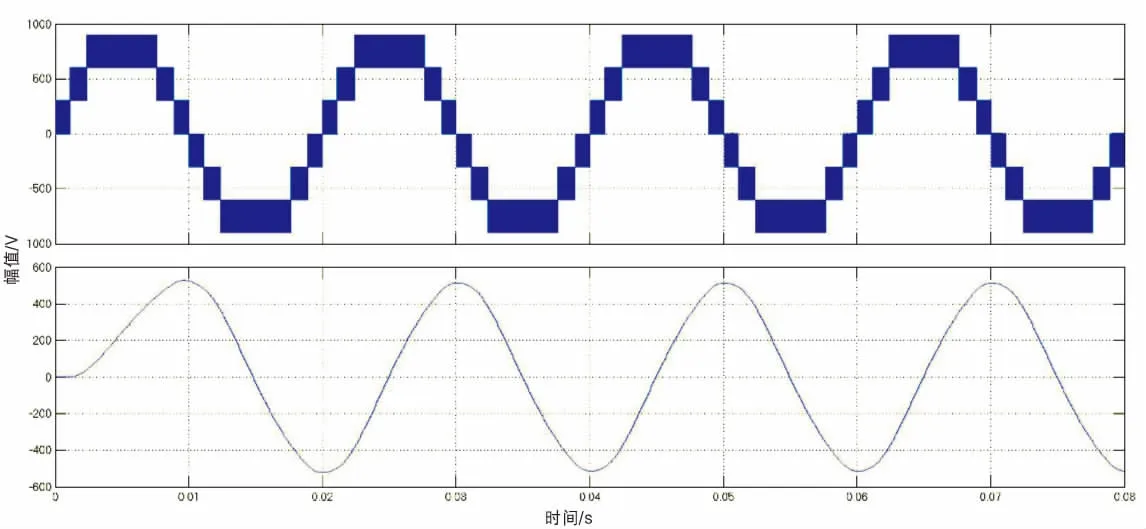
图7 多电平并网逆变器输出电压波形Fig.7 The waveforms of output voltage of three-level grid-connected inverter

图6所示为加入中点电位控制后的直流侧电容中点电位的波形,由图可知直流电容电压在±10V内波动,中点电位保持在滞环的环宽范围内,具有良好的稳定性能,实现了有效的中点电位平衡,证明了该闭环控制中点电位方法的有效性和可行性.

图7分别为多电平逆变器输出相电压、线电压和线电压的基波分量.由图可知线电压为多电平阶梯波,验证了逆变器的多电平特性,本文采用的改进SVPWM算法能使多电平逆变器输出期望的电压波形.

图8为分别对传统的SVPWM调制算法和改进SVPWM调制算法输出的线电压采用傅里叶变换进行谐波分析的对比图,其中横坐标为频率，单位Hz，纵坐标为各次谐波所占基波幅值的百分比.由谐波对比分析结果可以看出,相对于传统SVPWM调制,采用带有中点电位控制的改进SVPWM调制算法的总谐波畸变率(THD)大大减小,由15.5%减小到8.8%,传统的SVPWM中直流分量占基波百分比为3.2%,引入了中点电位平衡的改进SVPWM减少了直流分量,减弱了线电压的畸变,抑制谐波产生,提高了交流侧的功率因数.

(a) 传统SVPWM调制方法 (b) 改进SVPWM调制方法图8 输出线电压谐波分析对比图Fig.8 The comparison of harmonic spectrum of line voltages

4 总结

由以上风电并网多电平逆变器的理论与仿真分析,可以得出以下结论:

1)通过对SVPWM算法的本质分析,在120°坐标系下对SVPWM算法进行推导,得到了SVPWM各相调制波的简化算法数学表达式,避免了传统的SVPWM算法求解时必须的三角函数和求根运算,大大减小了运行时间,提高了运行效率.

2)将直流侧中点电压偏差引入到多电平逆变器闭环控制中,结果证明该方法能确保多电平逆变器在风电并网系统中具有良好的网侧性能和中点电压平衡特性.

综上,采用的改进SVPWM控制多电平逆变器方法可以满足风力发电系统的并网需要,维持了并网电压的稳定和可靠,为实际中实现具有较高电能质量的风电并网提供了理论基础.

[1] 郭家虎,顾先明,李鹏鹏.大功率MMC换流站最近电平调制策略研究[J].电气应用,2015,3(34):44-47.

[2] 王晓明,肖雯娟.直驱式风力发电并网逆变器的仿真分析[J].科学技术与工程,2011,28(11):6846-6854.

[3] BLASKO V,KAURA V.A new mathematical model and control of a three-phase AC-DC voltage source converter[J].IEEE Transactions on Power Electrics,1997,12(1):116-123.

[4] 刘昊.非正交坐标系SVPWM理论分析与混合型APF应用研究[D].北京:华北电力大学,2005.

[5] 周卫平,吴正国,唐劲松.SVPWM的等效算法及SVPWM与SPWM的本质联系[J].中国电机工程学报,2006,26(2):133-137.

[6] ZHOU K,WANG D.Relationship between space vector modulation and three phase carrier based PWM:a comprehensive analysis[J].IEEE Trans on Industrial Electronics,2002,49(1):186-196.

[7] WANG FEI.Sine-triangle versus space-vector modulation for three-level PWM voltage-source inverters[J].IEEE Trans on Industry Applications,2002,38(2):500-506.

[8] 陈娟,何英杰,王新宇,等.多电平空间矢量与载波调制策略统一理论的研究[J].中国电机工程学报,2013,33(9):71-78.

[9] 张志,谢运祥,乐江源,等.消除中点电位低频振荡的多电平逆变器空间矢量脉宽调制方法[J].电工技术学报,2011,26(3):103-109.

[10] 宋强,刘文华,严干贵,等.基于零序电压注入的多电平NPC逆变器中点电位平衡控制方法[J].中国电机工程学报,2004,24(5):57-62.

[11] 刘斌,黄凯伦,伍家驹,等.一种具有中点电位平衡可降低损耗的多电平空间矢量调制方法[J].电工技术学报,2015,30(4):196-202.

[12] 毕既华.非隔离型三电平光伏逆变器抑制共模漏电流和中点平衡方法[J].电气应用,2015,3(34):58-63.

责任编辑：时凌

ResearchonMulti-levelWindPowerGridInverterBasedonImprovedSVPWM

LI Qin,LI Shaowu,LIAO Honghua,AI Qing,GAO Shihong

(School of Information Engineering,Hubei University for Nationalities,Enshi 445000,China)

Aiming at the problems of complex Space Vector Pulse Width Modulation (SVPWM) and neutral point voltage fluctuation of three-level neutral point clamped inverter in wind power system,an improved SVPWM modulation method is presented in this paper.The linear calculation is used to simplify the three-level SVPWM algorithm and increase the efficiency instead of the numerous trigonometric functions and squre-root function in the traditional three-level SVPWM algorithm under the 120°coordinate system.The neutral point voltage error is introduced in the improved SVPWM algorithm to adjust the acting time of small vectors and the DC-link neural point voltage balance control is solved.The model of active inverter part of wind power grid-connected system with this improved SVPWM modulation has been simulated,the simulation results verify the feasibility and effectiveness of the proposed strategy,which provides theoretical basis on completing wind power grid integration of high power quality in practice.

space vector pulse width modulation;multi-level inverter;linear calculation;neutral point voltage;wind power grid-connected

2017-06-23.

湖北省教育厅科技项目(Q20161901);湖北民族学院博士启动项目(MY2013B024).

李沁(1981-)，女，博士，讲师，主要从事电力电子与新能源技术的研究.

1008-8423(2017)04-0453-05

10.13501/j.cnki.42-1569/n.2017.12.022

TM46

A