基于复杂系统理论的超导陀螺仪可靠性研究
朱 炼 ,吴房胜 ,张佑春 ,程 颖
(1.安徽工商职业学院 应用工程学院,安徽 合肥 231131;2.哈尔滨工程大学 自动化学院,黑龙江 哈尔滨 150001)
基于复杂系统理论的超导陀螺仪可靠性研究
朱 炼1,2,吴房胜1,张佑春1,程 颖1
(1.安徽工商职业学院 应用工程学院,安徽 合肥 231131;2.哈尔滨工程大学 自动化学院,黑龙江 哈尔滨 150001)
超导陀螺仪可靠性是超导陀螺仪研究的一个重要方面.首先研究了超导陀螺仪的组成、误差来源和网络拓扑图;然后分别运用复杂网络理论和复杂系统脆性理论对超导陀螺仪的可靠性进行了分析.通过分析,推断出了对超导陀螺仪可靠性产生较大影响的误差源和关键模块.
超导陀螺仪;复杂系统理论;可靠性
0 引言
陀螺仪是一种惯性器件,广泛地应用于军工和民用领域.超导陀螺仪是一种利用超导体的Meissner效应工作的新型陀螺仪,其理论精度比常规陀螺仪高几个数量级,适合于在导航中用作超导陀螺监控器.近年来,一些学者从不同方面对超导陀螺仪进行了研究.例如,文献[1-3]研究了超导陀螺仪转动系统的相关特性;文献[4-6]研究了超导陀螺仪支承系统的相关特性;刘建锋等[7]研究了超导陀螺仪信号读取的光电检测方法.超导陀螺仪的可靠性对其应用有着重要影响,本研究运用复杂系统理论来研究超导陀螺仪的可靠性,是一种新的尝试.
1 超导陀螺仪的组成及误差来源
超导陀螺仪主要由支承系统、转动系统、光电检测系统、壳体系统等部分构成.支承系统主要是保持陀螺仪转子悬浮.当有干扰使陀螺仪转子偏离中心时,支承系统能使转子回到中心.转动系统主要是保证陀螺仪转子旋转,包括转子起动、加减速、停止等.光电检测系统是检测出陀螺仪转子的偏转信息并通过解算得到角度等相关信息.壳体系统即外壳部分.支承系统、转动系统和光电检测系统是这几个部分中的重要部分.
超导陀螺仪支承系统主要由转子偏移测量电路、转子位置控制电路、信号源电路等组成,具体包括电容电桥电路模块、放大电路模块、相敏检波电路模块、滤波网络模块、校正网络模块、功率放大模块、转子控制模块、激励电源模块等.转动系统包括脉冲分配模块、放大电路模块、耦合电路模块、驱动电路模块、保护电路模块等.光电检测系统包括光电传感器模块、放大电路模块、解算电路模块、显示电路模块等.
超导陀螺仪的误差主要分为陀螺转子误差、球碗和电极误差、外界干扰与环境产生的误差等.陀螺转子误差主要包括转子静平衡误差、转子非球形误差、转子表面的刻线误差、转子离心误差等.球碗和电极误差主要包括球碗装配误差、电极球面误差、电极开槽误差、球碗开孔误差等.外界干扰与环境产生的误差主要包括外界振动或冲击、杂散磁场、系统真空度等因素产生的误差.
超导陀螺仪的可靠性由超导陀螺仪各模块和模块之间耦合的可靠性以及各种误差源对陀螺仪干扰引起的可靠性构成.总体来说,各个模块的设计较为成熟,系统产生故障从而引起可靠性问题一般是由于各个模块之间的耦合以及误差源对模块的干扰.不考虑各模块的内部组成,以各个模块和各种误差源为节点,以设计中各个模块之间的直接构成关系以及各种误差源对模块的直接影响为有向边,可以得到如图1所示的有向图.
图1中,实心黑节点为组成超导陀螺仪的各电路模块.其中,12节点表示电容电桥电路模块,13节点表示支承系统的放大电路模块,14节点表示相敏检波电路模块,15节点表示激励电源模块,16节点表示滤波网络模块,17节点表示校正网络模块,18节点表示功率放大模块,19节点表示转子控制模块,20节点表示光电传感器模块,21节点表示光电检测系统的放大电路模块,22节点表示解算电路模块,23节点表示显示电路模块,24节点表示脉冲分配模块,25节点表示转动系统的放大电路模块,26节点表示耦合电路模块,27节点表示驱动电路模块,28节点表示保护电路模块.空心节点为引起超导陀螺仪产生误差的误差源,其中,1节点表示转子非球形误差,2节点表示转子离心误差,3节点表示转子表面的刻线误差,4节点表示转子静平衡误差,5节点表示球碗装配误差,6节点表示电极球面误差,7节点表示电极开槽误差,8节点表示球碗开孔误差,9节点表示外界振动或冲击干扰,10节点表示杂散磁场,11节点表示系统真空度.
2 基于复杂网络理论的超导陀螺仪可靠性分析
对图1所示有向拓扑网络进行分析,求出各节点的出度、入度和总的度,如图2所示.
图2中,横坐标表示节点号,纵坐标表示节点的度.图2的图例中,O代表节点的出度,I代表节点的入度,D代表节点总的度.该网络节点的平均度为2.285 7.
该网络节点总的度的分布P(k)如图3所示.

图1 超导陀螺仪可靠性分析的有向拓扑图
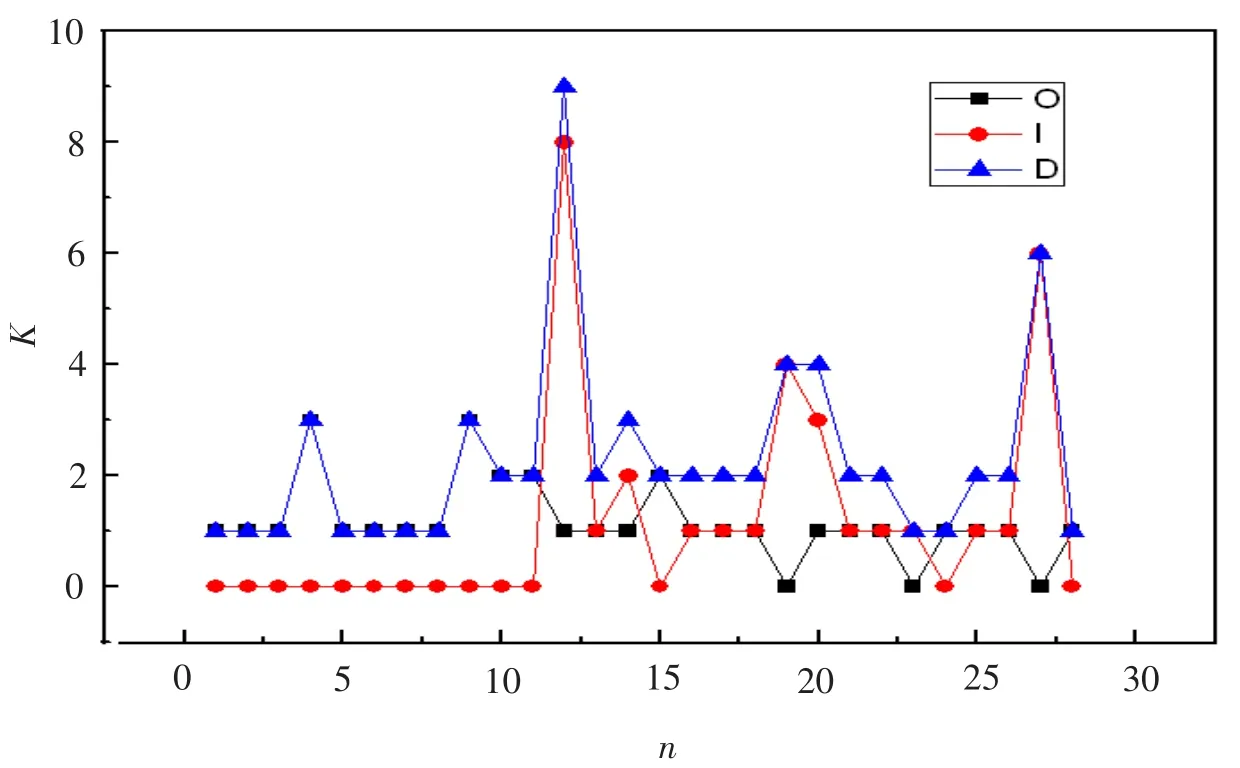
图2 网络各节点的度
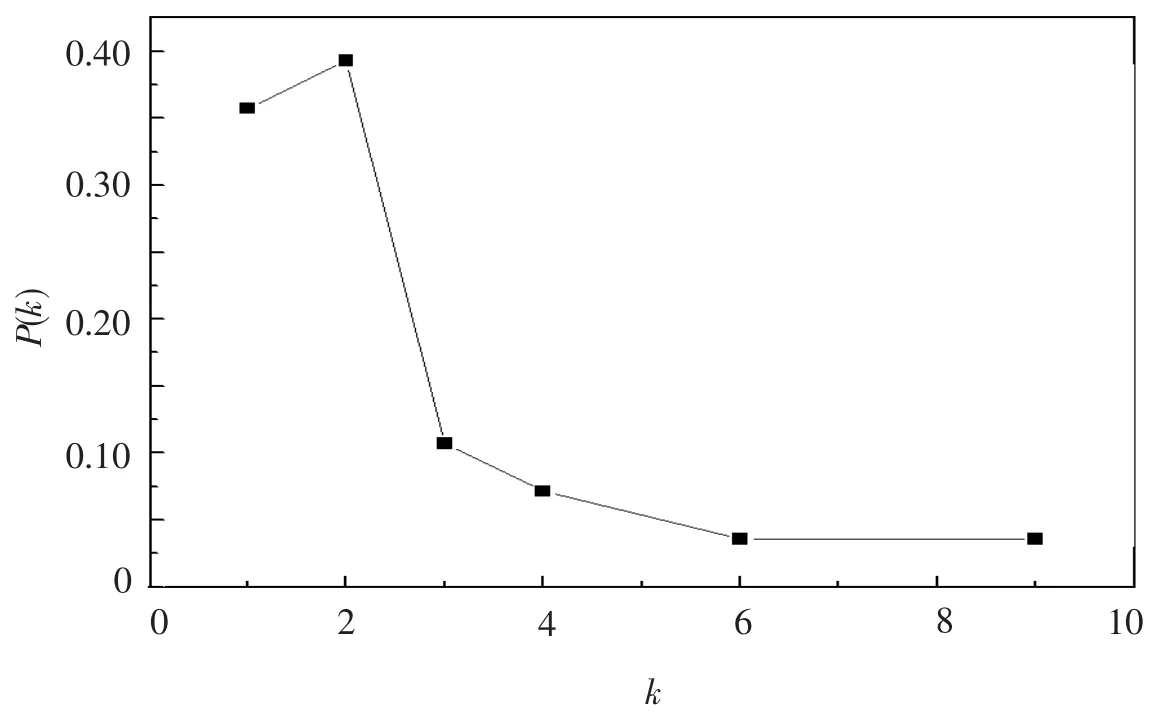
图3 网络节点总的度的分布
该网络的网络密度为0.084 7,为稀疏网络.该网络的稳健性较差,网络节点如果受到破坏,会影响整个网络的连通性. 从图 2、3 中可以看出,12 节点的度(9)最大,27、19、20 节点的度也较大,分别为 6、4、4,但节点12、27、19、20在度分布曲线中所占的概率不大,这说明节点12、27、19、20是网络中的关键节点.12节点表示超导陀螺仪支承系统的电容电桥电路模块,27节点表示超导陀螺仪转动系统的驱动电路模块,19节点表示超导陀螺仪支承系统的转子控制模块,20节点表示超导陀螺仪光电检测系统的光电传感器模块.这就要求需高度重视超导陀螺仪系统中的这几个模块的设计.
3 基于复杂系统脆性理论的超导陀螺仪可靠性分析
根据复杂系统的脆性理论[8],网络的脆性熵函数为:

式中,pi,j为节点i与节点j之间发生故障或者产生影响的概率
在该网络中,如果假设节点之间发生故障或者产生影响的概率相等,则络的脆性熵为:

考虑到模块和误差源之间的实际情况,运用Delphi法,得到:

网络的脆性熵为:

根据复杂系统的脆性理论[8],如果对系统进行控制后的脆性熵值小于控制前的脆性熵值,为有效控制.从计算的结果可以看出,运用Delphi法比等概率法得到的脆性熵值小.这说明运用Delphi法得到节点之间的发生故障或者产生影响的概率更符合实际情况.从Delphi法得到节点之间的发生故障或者产生影响的概率可以看出,节点9对节点12、20、27产生影响的概率较大,节点4对节点19、20、27和节点11对节点19、27以及节点3对节点20产生影响的概率也较大,这说明节点12、19、20、27所表示的电路模块的可靠性非常重要,同时,对节点3、4、9、11所表示的误差源对系统可靠性产生的影响要引起高度重视.
4 结语
随着技术的发展,组成超导陀螺仪各模块以及模块之间的故障概率将越来越小,其可靠性也越来越高.外界误差源对超导陀螺仪的干扰是影响超导陀螺仪可靠性的主要因素.运用复杂系统理论,可以分析出哪些误差源和哪部分模块对超导陀螺仪可靠性的影响较大,这对于进行超导陀螺仪设计时有针对性地提高其可靠性有重要意义.
[1]胡新宁,王厚生,王晖,等.超导转子旋转驱动装置的设计[J].光学精密工程,2010,18(1):169-174.
[2]杨再敏,胡新宁,崔春艳,等.一种基于迈斯纳效应的超导电机的驱动力的计算[J].低温与超导,2007,35(6):505-508.
[3]商木喜,戴银明,王秋良.一种基于迈斯纳效应的超导电机[J].中国惯性技术学报,2005,27(5):950-956.
[4]LIUJH,WANGQL,YANLG,etal.Analysisof Force Characteristics of a Superconducting Ballina Given Magnetic Field[J].Physica C,2009,469(13):756-759.
[5]汤继强.超导陀螺仪转子支承系统研究[D].哈尔滨:哈尔滨工程大学,2005:80-123.
[6]HEC,WANGQL.Force Characteristics Analysison a Superconducting Sphere Suspended by Spherical Coils[J].Cryogenics,2007,47(7):413-417.
[7]刘建锋,袁赣南,邹达明,等.一种新型陀螺仪信号提取方案的研究[J].哈尔滨工业大学学报,2005,37(8):1148-1150.
[8]吴红梅.复杂系统脆性理论及在煤矿事故系统中的应用[D].哈尔滨:哈尔滨工程大学,2008:41-52.
A Research on the Reliability of the Superconducting Gyroscope Based on the Complex System Theory
ZHU Lian1,2,WU Fang-sheng1,ZHANG You-chun1,CHENG Ying1
(1.School of Applied Engineering,Anhui Business Vocational College,Hefei,Anhui 231131,China;2.School of Automation,Harbin Engineering University,Harbin,Heilongjiang 150001,China)
The reliability of the superconducting gyroscope is an important aspect about the superconducting gyroscope researching.Firstly,the compositions and error sources and network topology of the superconducting gyroscope are researched.Then,the reliability of the superconducting gyroscope is analyzed by using the complex network theory and the complex system brittleness theory.The analysis concludes the key error sources and modules that greatly affect the reliability of the superconducting gyroscope.
superconducting gyroscope;complex system theory;reliability
N949
A
1673-1972(2017)06-0015-04
2017-09-24
安徽省高等学校自然科学研究重点项目(KJ2015A450、KJ2016A081、KJ2017A762);安徽省教育厅自然科学研究一般项目(KJ2016B006、KJ2017B003)
朱炼(1981-),男,湖北汉川人,副教授,博士研究生,主要从事复杂系统理论、精密仪器研究.
(责任编辑 钮效鹍)

