基于PFC2D的岩土体孔隙统计算法分析
,,,
(河海大学 a.岩土力学与堤坝工程教育部重点实验室;b.江苏省岩土工程技术工程研究中心,南京 210098)
2017,34(11):61-65,71
基于PFC2D的岩土体孔隙统计算法分析
袁俊平a,b,史宇宙a,b,丁国权a,b,王强林a,b
(河海大学 a.岩土力学与堤坝工程教育部重点实验室;b.江苏省岩土工程技术工程研究中心,南京 210098)
为了研究岩土材料微观孔隙结构特性,从机理上认识和掌握其宏观工程性质及其变化规律,基于PFC2D模拟岩土材料孔隙结构,对像素颗粒填充法的计算误差、像素颗粒尺寸选择及孔隙统计算法等进行了研究。研究结果表明:综合考虑误差控制与计算效率,建议最小土石颗粒半径的1/20为适合的像素颗粒半径;对比孔隙体积统计的3种算法发现,舍入法是相对最优算法。在此基础上实现了等效孔径分布的统计,为三维孔隙结构模型的研究提供了理论依据,为进一步对岩土材料孔隙结构特性及其与宏观力学行为和工程性质间关系的研究提供了基础。
孔隙结构;像素颗粒填充法;二维颗粒流软件;等效孔径分布曲线;舍入法
1 研究背景
岩土材料是一种多孔松散介质,其物理力学性质主要取决于其成因、物质成分、环境因素等。此外,岩土材料的微观结构特性在很大程度上也会影响其工程性质。微观孔隙特性是岩土材料重要的微观结构特性之一,对其渗透性、压缩性、持水特性等[1-2]有决定性影响。如土体被压缩时,由于土颗粒自身的压缩性很小,可以被忽略。因此,土体体积的减小就等于孔隙体积的减小。再如,孔隙率相同的2种试样,由于成因不同,其孔径分布可能有明显差异(如图1所示);显然,这2种土样的渗透性、土-水特征曲线等有很大的不同。因此,研究岩土材料微观孔隙结构特性,对从机理上认识和掌握其宏观工程性质及其变化规律有重要意义。

(a) 大量小孔隙 (b) 少量大孔隙
图1相同孔隙率试样的孔径分布差异示意图
Fig.1Differenceinporesizedistributionoftwospecimenswiththesamevoidratio
目前,测定岩土材料孔隙结构的方法主要有压汞法(MIP)[3-4]、CT扫描法[5-6]、核磁共振法(NMR)[7-8]等。这几种方法均基于试验观测结果,利用相应的后处理技术获取岩土的孔隙定量参数。由于岩土体是天然材料,即使由同一土料制备试样,其孔隙分布也往往有较大差异,从而造成测试结果重复性较差。而且这些测试方法都有一定的局限性,如压汞法只能测定试样中与外表面连通的开口孔的总孔隙率和孔径分布信息,无法获得孔隙间连通性等信息;CT法或核磁共振法则测试费用相对较高,目前尚难以得到广泛采用。数值模拟技术具有易于进行多次重复模拟、不受仪器尺寸限制、能全面统计各类孔隙大小及连通性等优势,逐渐被用于岩土体孔隙结构特征的研究中[9-10]。
数值模拟孔隙结构时常基于颗粒流软件(PFC),采用像素颗粒填充法。这种方法的基本思路是采用小的像素颗粒对试样区域进行填充,再通过一系列处理来获得孔隙结构。Navi等[11]较早采用了像素填充理论实现了对水泥块试样的微观孔隙结构的模拟,进而统计了其孔径分布曲线。随后,这种方法迅速被引入到岩土体的细观结构特征研究中。徐文杰等[12]建立了图像像素点信息与PFC2D像素颗粒之间的关系,提出了一种基于数字图像处理的非均质岩土材料细观结构的数值模型自动生成方法。丁秀丽等[13]对这种方法进行了改进,用填充像素颗粒生成团簇来模拟土石混合体中的碎石块,实现了由实拍数字图像直接生成土石混合体的颗粒流模型。金磊等[14]则将ANSYS所建立的不规则块石几何模型和PFC3D软件的颗粒填充理论结合起来,实现了三维不规则块石离散元模型的建立,进而进行了土石混合体大三轴试验的数值模拟。现有这些数值模拟研究主要针对土石颗粒,围绕颗粒形状、排列分布、配位数等与岩土体宏观力学性能的关系展开[15-16],而关于岩土体中孔隙结构特征的研究则很少见。
为简化问题起见,本文就岩土体的二维孔隙模型开展研究。基于PFC2D软件,研究岩土体孔隙结构建模方法,分析算法的效率和误差,就算法中参数选取和优化问题进行分析和讨论,进而实现岩土体孔径分布的统计。
2 孔隙结构的模拟
本文采用PFC2D软件[17]进行孔隙结构统计算法的分析和讨论,采取如下思路实现土石颗粒间孔隙结构的识别和可视化。
在预先生成的土石颗粒结构体系(图2(a))中,用小的像素颗粒填充整个土石区域(图2(b)),将土石颗粒以及与土石颗粒重叠的像素颗粒删除,从而得到由像素颗粒表示的孔隙结构(图2(c))。

图2土石颗粒体系孔隙结构的生成
Fig.2Formationofporestructureofparticleassemblies
PFC软件在生成每个颗粒时需要记录该颗粒的位置、大小、材料性质等相关信息,占用相应的内存。因此,生成颗粒数量较多时,已生成颗粒越多,生成下一个颗粒的效率就越低。当计算区域较大、像素颗粒尺寸较小时,随着像素颗粒逐步生成,计算机系统内存消耗急剧增加,导致算法执行效率迅速降低。
为解决这一问题,提出如下改进思路:在生成像素颗粒前,先判断即将生成的像素颗粒圆心(位置点)与土石颗粒的相对位置关系;再在需要保留像素颗粒的位置点上生成像素颗粒。这样,免去了不属于孔隙部分的像素颗粒的生成和删除过程,而只生成孔隙部分的像素颗粒,以实现提高计算效率的目的。
3 孔隙结构的模拟
实际工程中的土石料级配较复杂,粒径范围通常很广泛,土颗粒数目过多,在采用PFC软件模拟岩土体时常因颗粒单元有限而对土石级配进行简化[18]。实际土石颗粒形状大多不规则,PFC虽然可以使用团簇颗粒(clump)模拟不规则颗粒,但大多数PFC颗粒模型仍将土石颗粒简化为球型或圆盘形颗粒。本文的主要研究对象是孔隙结构,土石体系本身是次要的,因此算例选用简单的圆形土石颗粒模型。数值试样生成方法为:在5.0 m×10.0 m范围内,随机生成颗粒500个,最小半径0.108 5 m,颗粒最大最小粒径比为2.0(在此范围内粒径均匀分布),孔隙率为12%,设置切向、法向接触刚度均为1×108N/m,密度为1 900 kg/m3,摩擦系数为0.3;通过时步运行,使颗粒在重力作用下达到平衡状态。
PFC2D中基本单元为圆盘,因此选用圆形像素颗粒。由于相邻圆形像素颗粒间存在空隙,直接累加像素颗粒体积来确定孔隙体积会产生误差。为减少这种误差,统计各像素颗粒体积时按其外接正方形的体积4r2来计算(r为圆形像素颗粒的半径)。
3.1 像素颗粒尺寸的选择
为提高孔隙体积的统计精度,像素颗粒越小越好。但像素颗粒过小,则会导致需填充像素数量太多、计算量过大。为确定合理的像素颗粒尺寸,本文以上述试样为例,对比了不同像素颗粒尺寸时孔隙体积统计结果及计算耗时(见图3)。为对比统计精度,定义孔隙体积统计误差δ为
(1)
式中:V0为实际孔隙总体积,由土石总体积减去土石颗粒总体积确定;V*为统计得到的孔隙总体积。

(a)统计误差 (b)运算时间
图3孔隙体积统计误差和运算时间随像素颗粒尺寸变化曲线
Fig.3Curvesofstatisticalerrorofporevolumeandcomputingtimevaryingwiththesizeofpixels
由图3(a)可以看出,随着像素颗粒尺寸的减小,孔隙体积统计误差逐渐减小,当像素颗粒半径为最小土石颗粒半径的1/20时,孔隙体积统计误差lt;0.5%。值得注意的是,随像素颗粒尺寸减小,孔隙体积统计误差变化曲线逐渐变缓,表明当像素颗粒小到一定尺寸后,再通过减小其尺寸来降低孔隙体积统计误差的效果不明显。另一方面,若像素尺寸过大,则会造成个别极小孔隙无像素填充而被忽略统计的现象(如图4),这显然会导致孔隙结构统计结果的误差。

图4被忽略的孔隙
Fig.4Theignoredpores
从图3(b)可以看出,随着像素颗粒尺寸的减小,计算耗时迅速增加。特别是当像素颗粒半径小于最小土石颗粒半径1/40时,计算耗时曲线出现明显转折,表明像素颗粒小于该尺寸后计算耗时将大幅度增加。综合考虑孔隙体积统计误差和运算效率,结合算例检验发现,像素颗粒半径为土石颗粒最小半径的1/20是较为合适的。
3.2 填充像素处理算法比较
当根据某个位置点是否与土石颗粒重叠从而确定是否在该位置点生成像素颗粒时,根据具体处理方式的不同,可细分为3种方法:舍入法、全删法、有效体积法(见图5)。

图53种孔隙体积统计方法
Fig.5Threestatisticalmethodsforporevolume
下面分别介绍这3种方法并分析其误差。
(1)舍入法。根据像素颗粒与土石颗粒重叠部分占的比例来决定是否生成该位置点的像素颗粒。当像素颗粒位置点与土石颗粒间圆心距小于土石颗粒半径(即满足式(2))时,不在该位置点生成像素颗粒,反之则生成。这种处理方法相当于对填充的像素颗粒进行了“舍入”处理(图5(a))。
Rdlt;rb。
(2)
式中:Rd为位置点与土石颗粒间的圆心距;rb为土石颗粒半径。
(2)全删法。当像素颗粒位置点与土石颗粒间圆心距小于土颗粒半径与像素颗粒半径之和(满足式(3))时,则不在该位置点生成像素颗粒,反之则生成。采用这种处理方法仅生成了完全位于孔隙空腔内的像素颗粒,与土石颗粒有重叠的像素颗粒被“全删”,不生成(图5(b))。
Rdlt;rb+rp。
(3)
式中rp为像素颗粒半径。
(3)有效体积法。计算统计孔隙体积时,以不与土石颗粒重叠的像素颗粒体积作为“有效体积”。当位置点与土石颗粒间圆心距小于土石颗粒半径与像素半径之差时(满足式(4)),其有效体积为0,不生成该像素颗粒,反之则生成,并由几何运算确定其有效体积(图5(c))。以图5(c)中A像素为例,其有效体积为扣除与土颗粒重叠部分后的像素颗粒体积。
Rdlt;rb-rp。
(4)
如图5所示,用上述3种方法对同一孔隙填充像素颗粒时,有效体积法填充像素颗粒最多,全删法填充像素颗粒最少,而舍入法居中。
以上述试样为例,对比了这3种算法统计孔隙体积时的误差,见图6。

图6孔隙体积统计误差随像素颗粒尺寸变化曲线
Fig.6Curvesofstatisticalerrorsofporevolumebydifferentalgorithmsvaryingwiththesizeofpixels
由图6可以看出,全删法的孔隙统计体积误差较大,像素半径与土石颗粒最小半径之比达到1/80时仍存在7%左右的误差。有效体积法所统计得到的孔隙体积误差较小,像素半径与土石颗粒最小半径之比达到1/20时,其孔隙体积统计误差lt;5%。但采用该算法时,由于保留像素过多,可能出现原本2个不连通孔隙连通成为一体的情形(如图7)。由舍入法统计得到的孔隙体积与有效体积法的统计结果接近,而且采用该法进行孔隙体积统计时,未出现错误判断孔隙连通性等问题。综合上述的分析可见,3种算法中舍入法孔隙体积统计精度较高,孔隙形态与实际偏差较小,是相对最优的算法。

(a) 颗粒孔隙 (b) 有效体积法孔隙结构
图7有效体积法孔隙体积统计问题
Fig.7Problemonstatisticalvolumeofporebyeffectivevolumemethod
4 等效孔径分布曲线
对上述方法生成的孔隙结构,先通过PFC内置的fish语言的接触功能函数(Contact Functions)判断某像素颗粒周围与之接触的像素颗粒;再将相互接触的像素颗粒合并,组成一个颗粒团簇(clump);最后对每个颗粒簇进行体积统计,进而得到该颗粒簇所代表的单个孔隙的体积。本文采用8连通方式判断像素颗粒间的接触。
孔隙率相同、级配不同的2个试样的基本物理力学参数见表1。

表1 试样基本物理力学参数
对这2个试样运用舍入法得到其孔隙结构,统计孔隙体积进而得到等效孔径分布曲线(图8)。
图8中的等效孔径是由单孔隙体积按等体积换算得到的等效圆形孔隙直径。等效孔径分布曲线与颗粒级配曲线类似,表示了孔隙含量与等效孔径大小的定量关系[19]。尽管试样A、试样B的孔隙率相同,但两者等效孔径分布曲线有明显差异,表明2种试样的孔隙结构不同。以试样A为例,试样颗粒模型和所生成的孔隙模型如图9所示。
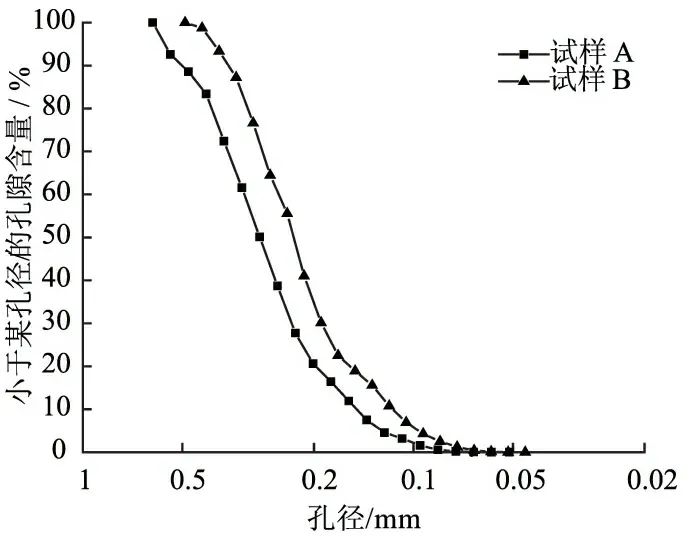
图8等效孔径分布曲线
Fig.8Curvesofequivalentporesizedistribution

(a) 试样颗粒模型 (b) 孔隙模型
图9试样A颗粒模型与孔隙模型
Fig.9ParticlemodelandporestructureofsampleA
采用文献[20]中的理论方法在获得的等效孔径分布曲线基础上,推导出2种试样的土-水特征曲线,见图10。两者的土-水特征曲线表现出明显的差异,而宏观的孔隙率无法反映这种差异。可见,采用本文所提出的孔隙统计算法,可以很好地反映土体孔隙结构及分布的特点,从而为从机理上揭示孔隙结构及分布与岩土体工程性质间的关系与规律提供新的途径。
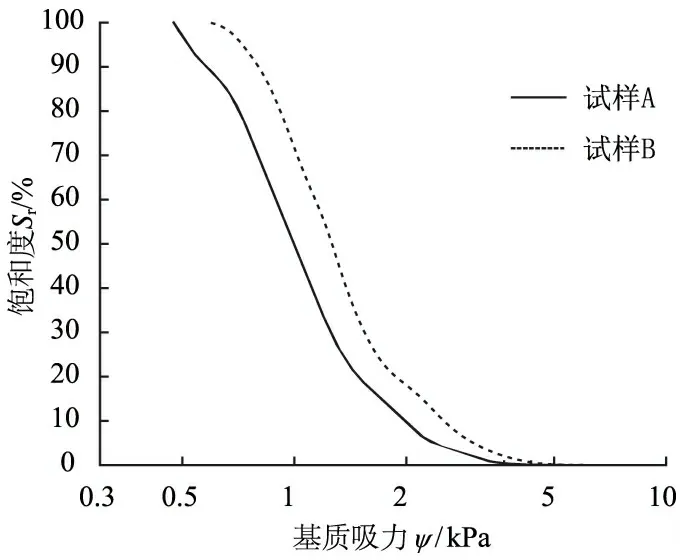
图10土-水特征曲线
Fig.10Soil-watercharacteristiccurves
5 结 论
本文基于PFC2D软件,对用像素颗粒填充法定量刻画岩土体孔隙结构时的像素颗粒尺寸选择、算法误差控制与优化等问题开展了研究,主要结论如下:
(1)综合考虑孔隙体积统计精度及计算效率,填充像素颗粒半径取土石颗粒最小半径约1/20较为合适。
(2)分析对比了3种孔隙体积统计算法(舍入法、有效体积法、全删法)的原理和统计误差,结果显示舍入法相对最优。
(3)在生成的孔隙结构模型的基础上,通过将填充孔隙的像素颗粒连接成颗粒簇的方法,实现了单个孔隙体积的统计,进而获得了试样的等效孔径分布曲线。
算例结果显示该方法可较好反映地岩土体孔隙结构分布特点。但本文的模拟结果与岩土材料实际孔隙结构及分布仍有差异。通过三维建模,考虑土石颗粒的不规则形态,以及采用更接近实际土石结构的级配可使模拟更符合实际情况。通过PFC建立的孔隙模型,采用合理的统计算法,不仅可以获得孔隙分布特征,还可以进行孔隙配位数、连通信息和孔隙形态等特征的统计,从而进一步建立微观孔隙特征与宏观力学行为之间的关系。从孔隙结构角度分析和揭示岩土体宏观工程性质,还值得进一步深入研究。此外,相关软件和计算机技术的发展使得大量颗粒单元模拟成为可能,从而可以建立更复杂的土石颗粒模型和更精确的孔隙结构模型,大大提高模拟的精度。
[1] 程亚南, 刘建立, 张佳宝. 土壤孔隙结构定量化研究进展[J]. 土壤通报, 2012,43(4): 988-994.
[2] 高建伟, 余宏明, 钱玉智, 等. 重塑黄土崩解特性试验研究[J]. 长江科学院院报, 2014, 31(10): 146-150,155.
[3] WATABE Y, LEROUEIL S, BIHAN J P L. Influence of Compaction Conditions on Pore-size Distribution and Saturated Hydraulic Conductivity of a Glacial Till[J]. Canadian Geotechnical Journal, 2000, 37(6): 1184-1194.
[4] 田 华, 张水昌, 柳少波, 等. 压汞法和气体吸附法研究富有机质页岩孔隙特征[J]. 石油学报, 2012,33(3): 419-427.
[5] PERRET J, PRASHER S O, KANTZAS A,etal. Preferential Solute Flow in Intact Soil Columns Measured by SPECT Scanning[J]. Soil Science Society of America Journal, 2000, 64(2): 469-477.
[6] ELLIOT T R, HECK R J. A Comparison of Optical and X-ray CT Technique for Void Analysis in Soil Thin Section[J]. Geoderma, 2007, 141(1/2): 60-70.
[7] MANTLE M D, SEDERMAN A J, GLADDEN L F. Single and Two-phase Flow in Fixed-bed Reactors: MRI Flow Visualization and Lattice-Boltzmann Simulations[J]. Chemical Engineering Science, 2001, 56(2): 523-529.
[8] 李杰林, 周科平, 张亚民, 等. 基于核磁共振技术的岩石孔隙结构冻融损伤试验研究[J]. 岩石力学与工程学报, 2012,31(6): 1208-1214.
[9] VOGEL H J. A Numerical Experiment on Pore Size, Pore Connectivity, Water Retention, Permeability, and Solute Transport Using Network Models[J]. European Journal of Soil Science, 2000, 51(1): 99-105.
[10] PAN C X. Use of Pore-scale Modeling to Understand Flow and Transport in Porous Media[D]. North Carolina: University of North Carolina at Chapel Hill, 2003.
[11] NAVI P, PIGNAT C. Three-dimensional Characterization of the Pore Structure of a Simulated Cement Paste[J]. Cement and Concrete Research, 1999, 29(4): 507-514.
[12] 徐文杰, 胡瑞林, 王艳萍. 基于数字图像的非均质岩土材料细观结构PFC2D模型[J]. 煤炭学报, 2007, 32(4): 358-362.
[13] 丁秀丽, 李耀旭, 王 新. 基于数字图像的土石混合体力学性质的颗粒流模拟[J]. 岩石力学与工程学报, 2010,29(3): 477-484.
[14] 金 磊, 曾亚武, 李 欢, 等. 基于不规则颗粒离散元的土石混合体大三轴数值模拟[J]. 岩土工程学报, 2015,37(5): 829-838.
[15] 张 翀, 舒赣平. 颗粒形状对颗粒流模拟双轴压缩试验的影响研究[J]. 岩土工程学报, 2009, 31(8): 1281-1286.
[16] 孔 亮, 陈凡秀, 李 杰. 基于数字图像相关法的砂土细观直剪试验及其颗粒流数值模拟[J]. 岩土力学, 2013, 34(10): 2971-2978.
[17] 周 健, 池 永, 池毓蔚, 等. 颗粒流方法及PFC2D程序[J]. 岩土力学, 2000, 21(3): 271-274.
[18] 顾馨允, 路新瀛. PFC3D模拟颗粒堆积体的孔隙连通性初步研究[J]. 混凝土, 2009,(5): 11-14.
[19] 谈云志, 孔令伟, 郭爱国, 等. 压实过程对红黏土的孔隙分布影响研究[J].岩土力学,2010, 31(5):1427-1430.
[20] 丁国权. 掺砾心墙料土-水特征曲线室内试验研究[D]. 南京:河海大学, 2011.
(编辑:占学军)
Statistical Algorithms for Pore Size Distribution of Rock-soil Mass Based on PFC2D
YUAN Jun-ping1, 2, SHI Yu-zhou1, 2, DING Guo-quan1, 2, WANG Qiang-lin1, 2
(1. Key Laboratory of Ministry of Education for Geomechanics and Embankment Engineering, Hohai University, Nanjing 210098, China; 2. Jiangsu Research Center for Geotechnical Engineering Technology, Hohai University, Nanjing 210098, China)
The purpose of this research is to obtain the microscopic structural characteristics and the variation rules
of macroscopic engineering properties of rock and soil materials. We discussed the issues of statistical error, pixel size, and statistical algorithms for pixel-particle-filling method by simulating pore structures in rock and soil samples using PFC2D (2-dimensional particle flow code). Results show that taking into account both statistical error and algorithmic efficiency, we recommend 1/20 of the radius of the smallest particle as the proper radius for pixel-particle-filling used for pore structure statistics. We also compared three pore volume statistical algorithms and found that round-off method is the optimal. Moreover, we proposed a method to obtain the curve of equivalent pore size distribution, based on which further research works are able to be conducted on the 3D pore structures model, the characteristics of the pore structures and the relationship among these characteristics and macro-mechanical behaviors and engineering properties of rock-soil.
pore structure;pixel-particle-filling method;PFC2D;equivalent pore size distribution curve;round-off method
10.11988/ckyyb.20160795
2016-08-09;
2016-09-06
国家自然科学基金项目(51378008);中央高校基本科研业务费项目(B15020060)
TU43
A
1001-5485(2017)11-0061-05

