黄河流域干流河段水资源调配多目标优化模型

，，,3， ,4，,5， ,6

(1.河海大学 水文水资源学院，南京 210098；2.黄河水利科学研究院，郑州 450003；3.黄河勘测规划设计有限公司，郑州 450003；4.西北勘测设计研究院有限公司，西安 710065；5.华东勘测设计研究院有限公司，杭州 311122； 6.长江科学院 工程安全与灾害防治研究所，武汉 430010)

黄河流域干流河段水资源调配多目标优化模型

张翔宇1,2，董增川1，宋瑞明1,3，韩锐1,4，许波刘1,5，罗赟1,6

(1.河海大学 水文水资源学院，南京 210098；2.黄河水利科学研究院，郑州 450003；3.黄河勘测规划设计有限公司，郑州 450003；4.西北勘测设计研究院有限公司，西安 710065；5.华东勘测设计研究院有限公司，杭州 311122； 6.长江科学院 工程安全与灾害防治研究所，武汉 430010)

目前黄河水资源的分配手段仍存在不少问题，用水量同比例丰增枯减不利于黄河水量的合理利用，传统的调度方式也无法使资源、社会达到协调发展。根据黄河水资源的实际情况，考虑各地区用水的公平合理性，建立黄河干流河段多目标优化配水模型，采用改进遗传算法来求解河段优化配水问题。结果表明:经过改进遗传算法的优化求解，可以将黄河干流水资源量科学合理地分配到各河段，全区缺水率控制在10%以下，并且满足河道断面的生态流量需求，符合社会、生态对于水资源开发利用的要求，最大程度地发挥了水资源的综合效益。

黄河流域；水资源调配；多目标优化；改进遗传算法；河段配水

1 研究背景

当今各种水资源问题中，如何科学合理地利用有限的水资源成为水资源领域中的一个重要研究课题，其中寻求合理的水资源调配模式是解决这个问题的主要途径。河段配水是水资源调配方式的一种，它是根据当前存在的水利工程，按照一定的调度规则将有限的水资源合理有效地分配给区域内的各个用水单元。对于黄河干流的河段配水，既要考虑上游与下游的利益关系，又要兼顾各用水单元的公平性，同时还要考虑河道的生态需求，实质就是在满足基本的用水约束的前提下，将水资源在河道内与河道外进行合理分配，使水资源的使用效益最大[1]。针对黄流干流的实际特点，河段配水时应在八七分水方案的基础上，考虑地区发展的不均衡性对水资源需求程度的差异，根据水资源量与需求量的关系，对黄河干流水资源进行优化分配，提出科学合理的河段配水方案，使有限的水资源发挥最大效益[2]。

2 多目标河段配水模型的建立

2.1 河段配水原则

黄河干流河段配水以河道外用水需求和河道内生态需求为依据，并考虑各地区用水的公平合理性，对水资源进行空间上的合理分配。当水资源不能够满足各用水单元的要求时，河段配水模型会按照一定的规则扣除各用水单元的供水量。河段配水的基本原则如下：

(1)优先满足断面最小流量要求，确保黄河不断流，保证其正常发挥河流功能，这是一个硬性约束条件，必须满足。

(2)各用水单元的分配水量以八七分水方案为控制指标，实际分水指标不能超过八七方案值。八七分水方案是正常年份的黄河可供水量分配方案，已成为沿黄各省区水资源开发利用的指导性依据。各个省区总配水量，应首先以1987年国务院分水方案为基础，在此不考虑四川，因为其不从黄河干流取水。八七方案各省区分水指标见表1。

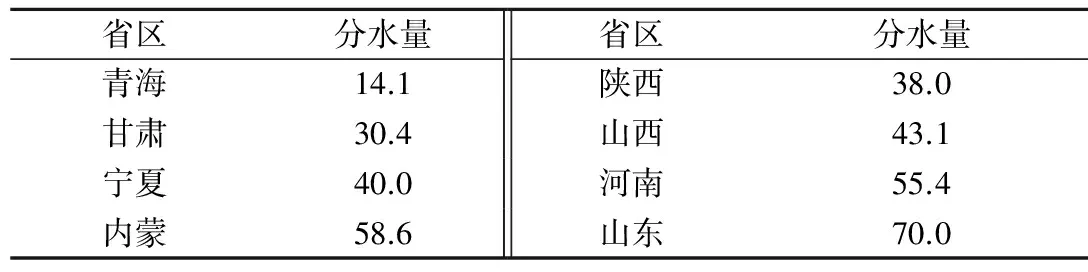
表1 八七方案各省区分水指标

(3)黄河流域地域广博，流经9个省区，各地区在分配黄河水时，应考虑当地经济社会发展状况、水土资源条件等因素，合理确定各地区的配水权重，使各地区的供水保证程度基本一致。各地区的供水水平、地区发展状况、农田灌溉效率等在时空上存在着较大差异，因此各地缺水严重程度是有区别的，水量分配的公平性不应简单地理解为 “一视同仁”，应重点保证严重缺水地区的抗旱用水，使水量短缺造成的损失尽可能降低[3]。在此针对各个省区情况选取水资源开发利用水平、人均用水量、万元GDP用水量、农田灌溉亩均用水和综合需水定额5个评价指标，建立配水权重评价指标体系。

其中水资源开发利用水平反映该地区是否充分利用当地水资源，低利用率的地区其配水权重应比其他地区要小，以促进其充分利用当地水资源；人均用水量侧面反映了地区水资源量的富足程度，人均用水量大说明该地的水资源量比较充足，可以适当减小其权重；万元GDP用水量反映了地区的社会经济发展水平，万元GDP用水量大说明该地区发展较滞后、水资源浪费严重，其配水权重应减小；农田灌溉亩均用水反映该地的农业灌溉效率，农田灌溉亩均用水量大说明其灌溉效率较低，应减小其配水权重，以督促该地区加强农田改造和监督管理；综合需水定额表示地区单位面积上的需水，需水定额越大说明地区用水的紧张程度越严重，应增加该地区配水权重。利用模糊多因素、综合评价法计算配水权重，得出各省区的配水权重，如表2所示。

表2 各省区配水权重

各省区按权重配水比同比例配水更为科学合理，其根据不同地区对水资源需求的紧张程度赋予不同权重，权重大的地区适当增加配水，体现了优化分配的思想。

2.2 模型建立

2.2.1 目标函数

(1)河道外目标。根据拟定的配水原则，引入上述各地区配水权重，以河段缺水率最小为目标，通过合理调配、优化水量分配，可使河段缺水率达到最小且分布合理[4]，数学表达式为

(1)

式中：αi为用水单元i的配水权重；βj为j河段的配水权重；QDijt为t时段i用水单元j河段的需水量；QSijt表示t时段i用水单元从j河段的取水量；I为用水单元总数，I=8；J为河段总数，J=32。

(2)河道内目标。为了满足生态环境与防凌的要求，对于某些控制断面，必须保持一定的适宜流量，以断面生态环境需水或防凌流量需求满足度最大为目标，为了使目标函数表示为成本型目标函数形式，方便之后目标函数的处理，在此以逆生态需求满足度最小为目标，数学表达式为

(2)

式中：QRjt为t时段j河段下断面的下泄量；DEjt为t时段j河段河道内生态环境需水量或防凌需水量。

2.2.2 约束条件

(1)需水量约束。用水单元从河段的取水不得大于河段需水量，数学表达式为

QSijt≤QDijt。

(3)

(2)八七方案约束。根据“丰增枯减”的分水原则，将实际年份的可供水量与正常来水年份可供水量(370亿m3)对比，确定出实际年份各省份干流的分水指标，该指标作为各省分配水量的上限值。数学表达式为

(4)

式中：370表示正常来水年份的可供水量；QS表示当年黄河可供水量；Qi为用水单元i相应于370的分配水量；QSi为用水单元i实际年份的可供水量。

(3)河段水量平衡约束。数学表示式为

QRjt=QRj-1,t+QIjt-QSjt-QLjt+QTjt。

(5)

式中：QIjt为t时段j河段的区间入流；QSjt为t时段j河段的取水量，QLjt为t时段j河段的河道损失量；QTjt为t时段j河段的河道退水量。

(4)最小下泄量约束。为了保证黄河发挥其河流功能，对于某些控制节点，必须保证一定的下泄量，以断面最小生态流量或防凌流量为基础作为断面下泄量条件约束，表达式为

QRminjt≤QRjt。

(6)

式中QRminjt表示t时段河段j的最小下泄量。

(5)节点间水量关系约束。采用水文模拟法来计算河道演进过程，数学表达式为

QIjt+QTjt-QSjt-QLjt。

(7)

式中：Δt表示相邻断面传播时间；ΔT为计算时段。

(6)非负约束。数学表达式为

QRjt≥0 。

(8)

3 多目标模型求解

3.1 多目标分析

本文用权重法将前面建立的2个目标函数化成一个综合目标，通过综合目标的大小来反映综合效益的大小。由于2个目标函数均为成本型目标，并且取值都位于[0，1]区间内，因此不需要进行标准化处理，就可转化为综合目标。在此选用线性加权和法将多目标优化问题转化为单目标优化问题，其中权重系数的确定采用信息量权数法，最终求得本模型的综合目标函数为

f=0.46f1+0.54f2。

(9)

3.2 改进GA算法设计

传统遗传算法(Genetic Algorithm,GA)是一种简单通用、容易理解的全局搜索算法，通过对种群的选择、交叉、变异等操作，淘汰适应度低的个体，优秀的个体将遗传到下一代中，经过循环迭代，最终满足收敛条件时停止计算[5]。它在最优化问题的求解中有巨大的潜力，由于其操作简单、鲁棒性强[6]，在水资源优化问题中越来越频繁地被使用到。

3.2.1 引入拟随机Halton序列生成初始种群

在GA算法中，利用拟随机Halton序列代替伪随机序列可以产生差异度更低、均匀性更高的初始种群，该拟随机种群可以更充分地获取优良个体的信息，具有较强的代表性。Halton序列利用基本函数的逆函数生成低差异的随机序列，能够使任意长度的序列都可以均匀地分布在约束空间，其执行过程见如下所述。

任意选取整数n，该整数都可用以b(b≥2且为质数)为基的形式[7]来表示，即

n=djdj-1…d1d0=djbj+…+d1b+d0。

(10)

式中：n∈(1，N)，N为种群规模；dj∈{0，1，…，b-1}。

将上式反转，得到

φb(n)=d0/b+…+dj/bj+1。

(11)

对于不同的整数n，基数b已知，dj都存在且唯一，则可以得到基b下的一组Halton序列，即

Hb(n)={φb(1)，φb(2)，…，φb(n)}，

n=1,2,…，N。

(12)

利用拟随机Halton序列生成的初始种群分布更加均匀，在算法搜索中更有优势，生成的Halton初始种群的质量可以得到大大改善[8]。

3.2.2 算法自适应调整

针对传统遗传算法在后期遗传过程中进化缓慢、容易陷入局部最优解的问题，根据进化的自适应思想，改进交叉、变异策略，使交叉概率pc和 变异概率pn能够自适应改变[9]。数学表达式为：

(13)

(14)

式中：fmax为种群中最大的适应度；f为要变异个体的适应度；favg为所有个体适应度的平均值；f′为2个交叉个体中的较大值；各参数的取值为pc1=0.9，pc2=0.6，pn1=0.1，pn2=0.001。

3.3 模型求解

种群规模N的大小与解的搜索空间大小、目标函数极值点的多少成正比关系，但一般情况下N取[20,100]区间的数值，在此取N=50。迭代次数G=300。交叉概率Pc以及变异概率Pn的选取采用自适应调整策略。选取各用水单元从各河段的扣水比例作为决策变量，在GA算法的基础上，引入Halton序列与自适应交叉、变异算法(图1)。

图1改进GA算法流程

Fig.1Flowchartofimprovedgeneticalgorithm

具体实现过程：

(1)利用Halton序列选取基b=2与b=3生成大小为200的种群H。

(2)按各个个体适应度值的大小采用锦标赛法从H中选择N个个体，作为初始种群P(N)。

(3)对种群P中的个体进行交叉、变异操作生成种群Q(N)，然后将P和Q混合到一起组成新的种群R，这时R中有2N个可能解。

(4)对R中的所有可能解按个体适应度从小到大的顺序排序，计算个体相应的累计概率，通过随机生成一个(0,1)之间的数，看其落在哪个区间内来确定选中的个体，如此选取出N个可能解作为新的种群P。

(5)若不满足终止条件，则将新产生的种群P转入步骤(3)继续迭代，直至进化代数达到要求的代数为止。

4 结果分析

对于每个计算单元，利用上述GA遗传算法对2012年3—5月份各时段的配水模型进行求解，得到的最优解即是最终河段配水方案。由于文章篇幅有限，黄河干流河段较多，在结果展示中将其汇总为几个河段分区，分别为龙羊峡以上、龙羊峡—兰州、兰州—龙门、龙门—花园口、花园口以下5个分区，各分区的配水结果如图2、表3所示。

图2不同时段各分区配水结果对比

Fig.2Comparisonofwaterallocationresultamongsubareasindifferenttimeperiods

表3 3月份各省区的分区配水结果

从图2、表3可以看出，各用水单元在各时段的取水以兰州至龙门以及花园口以下2个河段分区为最多，并且2个分区的取水主要集中在3月份与4月份，而龙羊峡至兰州分区的取水量随着时段递增，龙门至花园口3月份的取水量较大，龙羊峡以上的上游河段取水单元较少，故其取水量较小。花园口以下有河南、山东2个用水大户，其中3月份的河段取水达到了15.9亿m3，占干流河段总取水的38.3%，而龙羊峡以上的河段配水量只有0.1亿m3，仅占总取水量的0.24%。

配水方案中全流域的缺水率控制在10%以下，其中甘肃、宁夏、内蒙的用水效率较低导致其权重系数较小，作为惩罚，这些地区的缺水率相比其他地区要大一些。而山西、河南、山东的权重系数较大，有更大的保证程度去获取黄河水量，相应的缺水率也小一些，分别只有7.59%,8.38%,7.23%。在干流众多河段中选取几个用水单元较多、用水量较大的典型河段展示配水结果，各时段的计算结果见表4。

表4 各时段典型河段配水结果

取水量较大的几个河段主要集中在黄河下游，分别为西霞院至花园口、艾山至泺口、泺口至利津，其中泺口至利津为山东的主要取水河段，共有青岛、烟台等6个地市在此取水，4月份取水量达到了7.29亿m3；青铜峡至石嘴山为甘肃、宁夏2省主要的取水河段，其在5月份的需求量较大，河段取水达到了7.45亿m3；循化至刘家峡为青海的主要取水河段，取水量较小，每个月份均在0.5亿m3以下。

5 结 语

黄河流域用水的高峰期主要集中在3—5月份，在这一时段黄河水量短缺的形势更加严峻。多目标河段配水模型是在保证黄河生态流量的基础上，遵循八七方案以及地区用水公平性的原则，运用改进GA算法从空间上对各时段的黄河水量进行优化分配，使得供水系统的缺水率最小并同时满足河道内的生态流量需求，最终计算结果科学、合理，有效提高了黄河水资源利用率。但由于区域水资源调配问题的复杂性，用水单元权重指标的选取以及河段配水权重的计算有待进一步深入研究与讨论。

[1] 张一清.水资源优化配置的制度研究[J].长江科学院院报,2010,27(7):6-11.

[2] 彭少明,王 浩,王 煜,等.泛流域水资源系统优化研究[J].水利学报,2013,44(1):10-17.

[3] 王道席,胡和平.黄河下游引黄灌区按权重配水模型研究[J].灌溉排水学报,2002,21(2):5-7.

[4] 彭少明,郑小康,王 煜,等.黄河典型河段水量水质一体化调配模型[J].水科学进展, 2016,27(2):196-205.

[5] 杨建文,李志鹏,刘 忠,等.基于初始种群变异遗传算法的水电站优化调度[J].人民黄河, 2015,37(5):116-118.

[6] 郑 姣,杨 侃,倪福全,等.水库群发电优化调度遗传算法整体改进策略研究[J].水利学报, 2013,44(2):205-211.

[7] 黄冬民,潘 泉,梁新华.基于随机化Halton序列的粒子滤波算法研究[J].计算机应用研究, 2011,28(1):91-94.

[8] 郭 凯.遗传算法的3种改进方法和分析[J].电子测试,2011,(3):38-40.

[9] 任子武,伞 冶.自适应遗传算法的改进及在系统辨识中应用研究[J].系统仿真学报, 2006,18(1):41-43.

(编辑：罗 娟)

Multi-objective Optimization Model of Water Resource Allocation for Mainstream Channel Segment of Yellow River Basin

ZHANG Xiang-yu1,2，DONG Zeng-chuan1，SONG Rui-ming1,3，HAN Rui1,4，XU Bo-liu1,5，LUO Yun1,6

(1.College of Hydrology and Water Resources, Hohai University, Nanjing 210098, China; 2.Yellow River Institute of Hydraulic Research, Zhengzhou 450003, China; 3.Yellow River Engineering Consulting Co., Ltd., Zhengzhou 450003, China; 4. Northwest Engineering Corporation Limited, Xi’an 710065, China; 5. Huadong Engineering Corporation Limited, Hangzhou 311122, China; 6. Engineering Safety and Disaster Prevention Department, Yangtze River Scientific Research Institute, Wuhan 430010, China)

Due to problems in the water resources allocation of Yellow River basin, the method of water consumption in proportional increase or decrease with the increasing or decreasing of river discharge may have negative effects on rational water utilization. Traditional scheduling methods could not coordinate the harmonious development between resources and society. In view of this, a multi-objective optimization model for water resource allocation was established in consideration of the impartiality and rationality of regional water use based on the actual situation of the Yellow River. Furthermore, the model was solved by applying improved genetic algorithm. Research results show that through the improved genetic algorithm, water resources of the mainstream Yellow River can be rationally and scientifically allocated to different segments. The rate of water scarcity in the whole study area is below 10% and the water allocation results meet the requirements of ecological flow of river cross-section, which also conform to the ecological and social requirements of development and utilization of water resources. The comprehensive benefits of water resources developed to the greatest extent.

Yellow River basin; water resources allocation; multi-objective optimization; improved genetic algorithm; water allocation of channel segment

10.11988/ckyyb.20160775 2017,34(11):18-22

2016-07-31；

2016-09-05

国家自然科学基金面上项目(41471014)；国家社会科学基金项目(2012amp;ZD214)

张翔宇(1991-)，男，河南焦作人，硕士研究生，研究方向为水资源规划与管理，(电话)13526636824(电子信箱)xyzhang_91@126.com。

董增川(1963-)，男，山西芮城人，教授，博士生导师，博士，主要从事水资源规划与管理的研究，(电话)13705185693(电子信箱)zcdong@hhu.edu.cn。

TV211.11

A

1001-5485(2017)11-0018-05