应用质点动力学的潮汐力分析

胡雪兰 张艳峰 Joël FLAHAUT

（中欧航空工程师学院/中国民航大学 天津 300300）

应用质点动力学的潮汐力分析

胡雪兰 张艳峰 Joël FLAHAUT

（中欧航空工程师学院/中国民航大学 天津 300300）

从质点运动学基本定律出发，分析了太阳系中天体的运动对于地球表面潮汐项的影响，用简单通用的物理定律解释了潮汐现象的成因，有助于大学生将理论知识应用于解释物理现象的能力的提高，激发学生学习大学物理的兴趣。

潮汐力 参考系 运动学基本方程

潮汐是沿海地区的一种自然现象，指的是海水在垂直于海洋面方向周期性的涨落现象。在白天的称为“潮”，在夜间的称为“汐”。海水在垂直方向的涨落具有一定的周期性，一般每个月会有两次大潮，分别为农历的初一和十五。潮汐的升降和涨落，与人们的多种活动有密切的关系，如船只航行及进港出港、舰艇活动、沿海地区的农业、渔业、盐业、港口建设、大地测量、环境保护等，都必须掌握潮汐变化的规律[1,2]。此外，利用潮汐进行发电，也是能源开发的一个重要方面。

潮汐现象主要是由于月球和太阳的万有引力引起的。但是,太阳和月球相对于地球的相对运动为什么会影响海水涨落，影响有多大呢。本论文将从非惯性参考系中的动力学基本方程出发，来分析影响海水垂直方向涨落的潮汐力。

一、潮汐项的推导

1.在地球参考系中的加速度

在研究大海中的水滴相对于地球表面运动之前，我们先定义如下物理量：

将大海中质量为m的水滴定义为质点M，M点在地轴上的投影用H表示，地球的中心用O表示，O点在哥白尼参考系(RCop)中的运动代表地球在太阳系中相对于太阳系的质心的运动，地球在RCop中的加速度用表示。地球在质点M处产生的万有引力场用表示，除地球之外的太阳系中其他天体在M处的总的引力场用表示，水滴相对于地球表面的运动速度用表示，水滴相对于地球表面的加速度用表示。

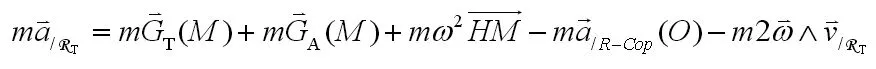
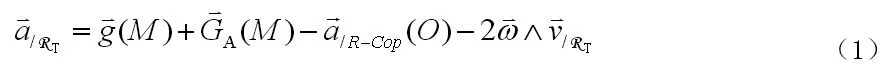
2.潮汐项的推导

因此（1）可以变为

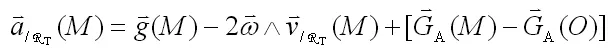
二、潮汐项的分析

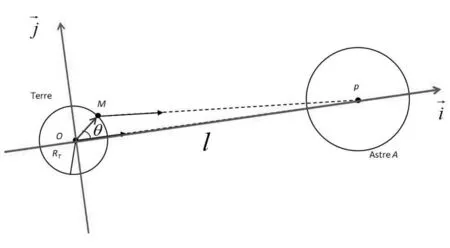
图1 以地心和第i个天体中心P的连线为i轴建立的坐标系

图1 为以地心和第i个天体的中心P的连线为i轴，与i轴垂直的方向为j轴建立的坐标系。Oij平面为平行于黄道面（非赤道面）的平面，M为地面上的点（位于Oij平面内）。假设第i个天体也位于该平面上（太阳本身就在该面内，月亮的公转平面与黄道面夹角为5.1°，可以近似认为月球也在黄道面内）。为与的夹角。则

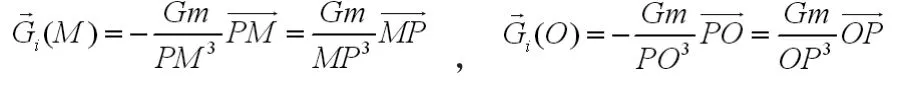
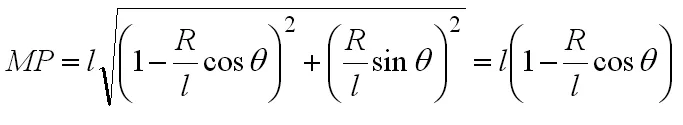
潮汐项可以化为：

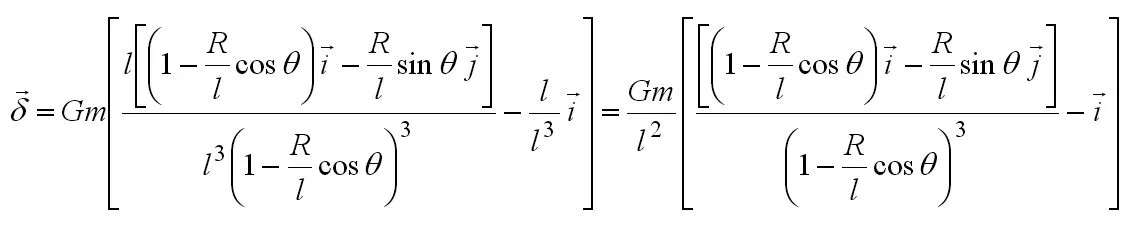
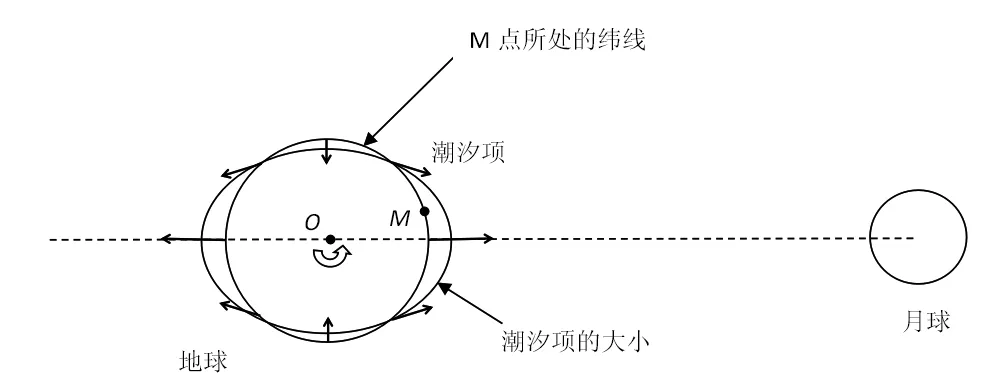
图2 月球对于地球表面某一纬度的潮汐项的影响大小示意图

图2是根据公式（3）分析所得地球表面某一纬度受到月球影响的潮汐项的大小分布示意图。在和时，潮汐力最大。

下面我们分析不同的天体对于地球表面潮汐力影响的大小。有公式（2）可得太阳系中某一个天体对于地球表面M点的潮汐项影响的大小为：

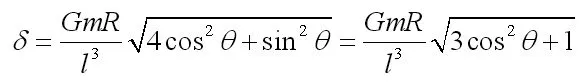
表1为太阳、月球、水星、金星、火星、木星和土星的质量、与地球的之间的距离以及由此计算所得对于地球表面潮汐项影响的最大值。

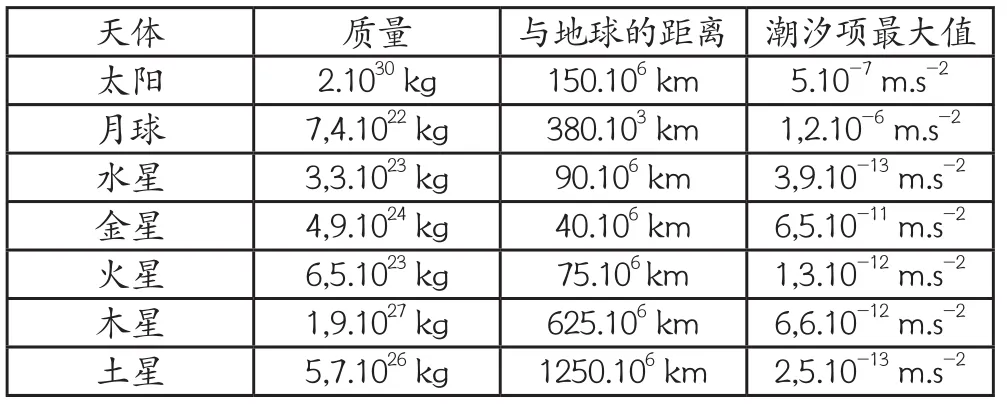
表1 太阳系中部分天体的质量、与地球的之间的距离以对于地球表面潮汐项影响的最大值

由表1 可知，每个天体对于潮汐项影响的最大值均远小于地球表面重力加速度9.8 m.s-2。太阳和月球对于地球表面的潮汐项影响最大，且月球的影响大于太阳的影响：，其他天体的影响远比太阳和月球的影响小得多，可以忽略不计。即地球上的引潮力主要受到月球和太阳的万有引力的影响。

当月球距离地球最近时，对潮汐项影响最大。每月阴历初一、十五，太阳，地球和月亮会基本处在同一直线上，会有两次大潮。在月球绕地球转动的同时，地球也在绕地轴做自转，因此，地球上一个地点，会出现两次潮水的张落，

当然，潮汐现象除了受太阳、月球与地球的相对运动影响之外，还受到海沟的形状、海岸线的形状对海水流动的影响。除此之外纬度、地潮和气潮等多种因素也对于流体流动有很大的影响[2，3]，在此对于这些因素，我们在此不做讨论，仅仅从质点动力学角度对潮汐力产生的原因进行分析。

三、结论

本文从质点运动学基本定律出发，通过在哥白尼参考系、地球参考系中研究地面上M点的水滴相对于地球表面的运动，分析了太阳系中天体的运动对于地球表面潮汐项的影响。此部分内容属于大学物理的范围，用简单通用的物理定律解释了潮汐现象的成因，有助于大学生将理论知识应用于解释物理现象的能力的提高，激发学生学习大学物理的兴趣。

[1]韩忠全.潮汐现象的成因及规律分析 [J]. 物理教学探讨2012，28（370）: 27-28.

[2]田晓岑 . 潮汐现象的成因 [J] . 大学物理 1996, 15（10）：24-27.

[3]宋海珍. 引力场中潮汐力的研究[J]. 河南师范大学学报(自然科学版 ). 33(1):49-52.

致谢：感谢中国民航大学院级优质建设课程《经典物理（上、下）》项目的资助。

G642

A

2095-3089（2017）24-0184-02