向量世界的“厚积薄发”

吴 菲

(江苏省南京市高淳区湖滨高级中学,江苏 南京 211316)

向量世界的“厚积薄发”

吴 菲

(江苏省南京市高淳区湖滨高级中学,江苏 南京 211316)

平面向量作为高考必考的内容，其应用性往往是学生薄弱的一块，本文就此进行讨论，希望引起共鸣.

向量；不等式；立体几何

图1

平面向量作为高中数学中重要的一章，历年来备受各种考试的重视，尤其是在高考中，更是雷打不动的出现.向量这一章以其灵活多变的题型和方法，对于学生而言，也是一个很大的重点和难点.向量作为代数和几何的综合体，向量问题本身的解决多半就有代数和几何的方法，尤其突出一点的是，向量可以作为一种工具，解决数学中很多其他的问题.本文就来谈一下关于向量在数学其他问题当中的应用，让我们来体会向量这个工具的优越性.

例1 如图1所示，无弹性的细绳OA，OB的一端分别固定在A，B处，同质量的细绳OC下端系着一个称盘，且使得OB⊥OC，试分析OA，OB，OC三根绳子受力的大小，判断哪根绳子受力最大．

解析本道题是高中物理当中的一道力的问题，其实在高中物理中，我们也提到了向量，但是跟高中数学当中有所不同的是， 物理当中没有数学中所表述的具体和集中，例如这道题，对于三根绳子的受力大小，其实就是我们所说的向量的模长.设绳子OA受力为a，OB受力为b，OC受力为c，由三力平衡可得a+b+c=0，由于b和c的夹角为90°，所以a=-b-c,两边取其模，可得|a|=|-b-c| ，由向量中|a|2=a·a，|a|2=|-b-c|2=(-b-c)2=b2+c2+2b·c=|b|2+|c|2,所以我们能看出a的模长最大，故而绳子OA所受的力最大，将这道题利用向量来解决，其实就是模长的问题，所以极大地简化了问题.

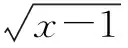
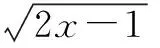
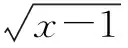
向量不仅在代数中有诸多应用，在立体几何问题中，点到点，点到线，点到面的距离，线面所成角，面面所成角，还有线面，面面的位置关系这些题型当中都有很大的优越性，使用向量的方法求解立体几何问题，其实就是一个将图形量化的过程，过程单一且直观，学生易掌握，以下举例说明.

(1)在平面PAB内找一点M，使得直线CM平面PBE，并说明理由；

(2)若二面角P-CD-A的大小为 ，求直线PA与平面PCE所成角的正弦值.

由已知，CD⊥PA，CD⊥AD，PA∩AD=A，

所以CD⊥平面PAD.于是CD⊥PD,

从而∠PDA是二面角P-CD-A的平面角，所以∠PDA=90°.

由PA⊥AB，可得PA⊥平面ABCD

设BC=1，则在Rt△PAD中，PA=AD=2

设平面PCE的法向量为n=(x,y,z)，

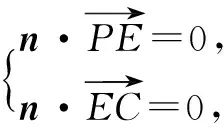
新课程加强了平面向量的应用，教材中也设计了不少用向量方法研究平面图形性质的问题，随着高考的改革，向量在中学数学中的地位应该越来越高，其灵活多变的形式，以及以上我们提到的向量的应用必将成为考试的热点，我期待此文投石问路，期待大家能利用向量解决越来越多的问题.

[1]中华人民共和国教育部.普通高中数学课程标准(实验)[S].北京：人民教育出版社，2003.

[2]刘玉斌.向量在几何中的应用[J].科技视野，2013(23)：133.

[责任编辑：杨惠民]

G632

A

1008-0333(2017)25-0012-02

2017-07-01

吴菲(1983.3-),女，安徽人，现任南京市高淳区湖滨高级中学教师，从事高中数学教学研究.