基于思维进化算法的电动汽车有序充电控制策略
余晓玲, 余晓婷, 韩晓娟
(1. 华北电力大学控制与计算机工程学院,北京 102206;2. 青海大学水利电力学院,青海 西宁 810016)
基于思维进化算法的电动汽车有序充电控制策略
余晓玲1, 余晓婷2, 韩晓娟1
(1. 华北电力大学控制与计算机工程学院,北京 102206;2. 青海大学水利电力学院,青海 西宁 810016)
大量电动汽车充电会加大充电站负荷峰谷差,影响充电站安全稳定运行。因此提出了一种基于思维进化算法(MEA)的电动汽车有序充电控制策略:以用户充电费用最少和充电站负荷峰谷差最小为目标函数,采用MEA算法动态计算接入充电站电动汽车的最优充电时段,由用户自主响应,从而实现充电站内电动汽车的有序充电控制。为验证该策略的有效性,利用蒙特卡洛方法模拟用户充电需求,对算例进行仿真分析。结果表明:与无序充电相比,有序充电控制策略可在降低电动汽车用户费用的基础上实现充电负荷的削峰填谷;相比于使用遗传算法,MEA算法具有一定优势。
电动汽车充电站; 蒙特卡洛模拟; 思维进化算法; 有序充电; 峰谷电价
0 引言
近年来,发展电动汽车被世界各国普遍确立为发展低碳经济和保障能源安全的重要手段[1,2],然而大规模电动汽车接入电网充电,将对电力系统运行产生一定影响[3],且会改变电网负荷特性。如果不采取有效的充电控制策略,将进一步加剧电网负荷峰谷差,可能导致配电网线路过载、电压跌落[4]、配电网损耗增加[5]、配电变压器过载[6,7]、谐波污染[8]等一系列问题。同时,电动汽车作为新型的移动负载,其充电行为具有较强的时空不确定性,无序充电将形成冲击性负荷,影响电网稳定。因此电动汽车有序充电控制对于降低电网运行风险,提高电网运行效益与稳定性具有重要意义[9]。
目前有关电动汽车有序充电的研究有:文献[10]提出了一种以降低配网网损为目标的电动汽车有序充电在线控制方法;文献[11]提出了面向电动汽车换电模式的两阶段有序充电方法;文献[12]提出了基于队列方式的功率控制优化充电策略;文献[13]在分析配电系统馈线网络损耗、配电网负载率以及负荷波动方差三者之间关系的基础上,研究用于降低损耗的有序充电控制方法。
上述文献中有序充电控制方法主要基于数学优化模型,通过动态控制充电功率实现有序充电,但并不适用于大规模电动汽车有序充电的在线应用。同时,有序充电过程会频繁调节充电桩充电功率,影响电池和充电机寿命,用户支持度较低[14]。
因此,文中提出了一种基于思维进化算法(MEA)的有序充电控制策略:通过峰谷电价引导电动汽车负荷转移。以用户充电费用最小和充电站负荷峰谷差最小为目标函数,以充电站功率平衡及满足用户充电需求为约束条件,建立电动汽车有序充电控制的优化模型,采用MEA算法对模型优化计算,得到电动汽车的最优充电时段,由用户自主响应,从而实现充电站内电动汽车的有序充电控制。
1 基于MEA算法的有序充电控制策略
文中提出的有序充电控制策略,主要是充电站根据峰谷电价和功率限制等条件,制定分时段充电计划,期望用户自主响应,通过电价引导达到降低峰谷差的目的。采用峰谷电价,是“电力需求侧管理”的一种重要手段,也是引导电力用户进行合理分时段用电的基本方式[15]。图1为有序充电控制策略流程。

图1 有序充电控制流程Fig.1 Flow chart of the proposed coordinated charging method
(1) 获得充电需求数据。电动汽车接入充电桩,充电桩通过电动汽车的电池管理系统得到该车电池容量B和初始电池荷电状态值S0,用户通过客户端输入其预期停留时间TL与预期充电后电池荷电状态值St。
(2) 计算预期充电时长。充电站的管理系统利用式(1)计算充电后电池荷电状态值达到St时的预期充电时长Tg。
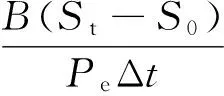
(1)
式中:「⎤为向上取整符号;Pe为充电桩输出的恒定功率;Δt为每个时间段的长度,文中取15 min。
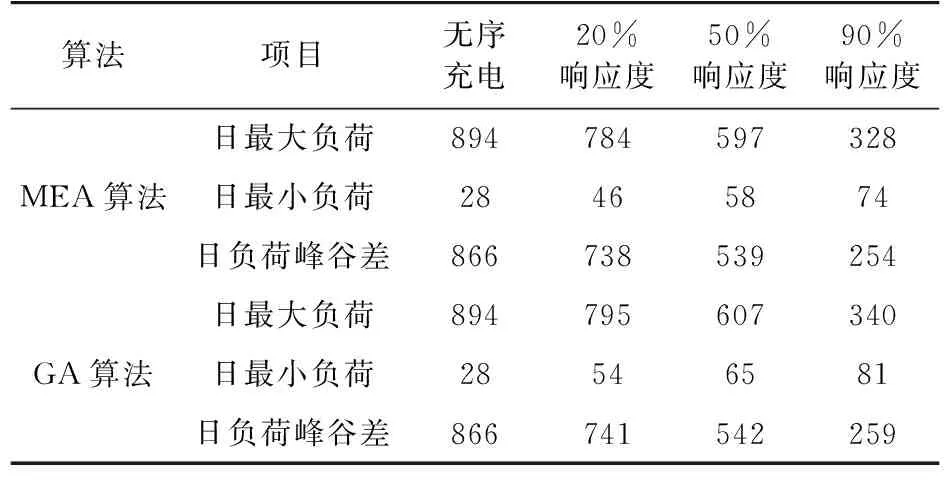
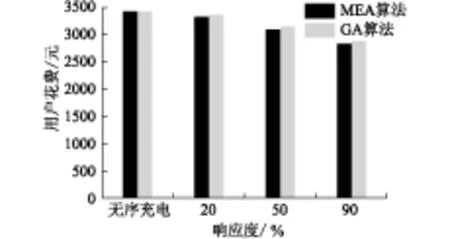
(3) 根据Tg计算结果,判断是否为正常情况。定义TL内满足负荷功率限制的时间段之和为充电站可充电时间Tp。如果Tg (4) 确定有序充电时间段。充电站利用电动汽车的充电需求与峰谷电价,采用MEA算法计算出有序充电时间段、有序充电费用及无序充电费用。 (5) 用户自主响应充电模式。由用户自主选择有序或无序充电,充电站根据用户选择确定最终充电计划,以实现电动汽车的有序充电控制。 (6) 异常情况处理。异常情况一:用户可以选择离开或继续充电。若用户想继续充电,需要延长TL或者降低St。若用户更改充电需求,则重复步骤(2)直到充电站可以满足用户的充电需求。异常情况二:用户可以选择无序充电、有序充电、更改数据或直接离开。由于不连续充电会对电动汽车电池造成一定损伤,故用户对该充电方式的响应度较低。若用户选择无序充电,则充电桩立即开始为电动汽车充电,充电时自动跳过不满足负荷约束条件的时间段;若用户响应有序充电,则无法保证用户连续充电,充电站系统会在充电站负荷最小的时间段内为电动汽车充电且该时段内为充电电价均为谷时电价,以补偿不连续充电给用户带来的损害;若用户选择延长TL或者降低St,则重复步骤(2),直到充电站可以满足用户的充电需求。 以用户充电费用最少和充电站负荷峰谷差最小为目标函数,如式(2)所示。 (2) 式中:f1为用户充电费用;cf为充电站峰时电价;cg为谷时电价;Tf,Tg分别为电动汽车在峰时段的充电时长和谷时段的充电时长;f2为充电站的负荷峰谷差;Pf为充电站负荷峰值;Pg为充电站负荷谷值。 (1) 功率约束。 Pcmin (3) 式中:P(i)为充电站第i时间段的功率;Pcmax为充电站可输出的最大有效功率;Pcmin为充电站可输出的最小有效功率。 (2) 荷电状态值约束。充电结束时电动汽车电池荷电状态需达到用户预期电池荷电状态值。 B(St-S0)≤ΔtNPe (4) 式中:N为可安排充电的时间段数。 MEA算法由孙承意等人于1998年提出,并且已被成功应用到解决复杂的组合优化问题[16]。该算法将群体划分为有生子群体和临时子群体,在此基础上定义的趋同和异化操作分别探测和开发解空间新的点,这两种功能相互协调且保持一定的独立性,便于分别提高效率。MEA可记忆不止一代的进化信息,这些信息可一直使趋同和异化向着有力的方向进行[17]。MEA算法流程如图2所示。 图2 思维进化算法流程Fig.2 Flow chart of MEA (1) 种群的初始化:利用初始化种群产生函数产生大小为s的种群;利用子种群产生函数产生大小为b的优胜子种群和大小为t的临时子种群; (2) 趋同操作:在子群体范围内,个体为成为胜者而竞争的过程叫趋同,一个子群体在趋同的过程中,若不再产生新的胜者,则称该子群体已经成熟。当子群体成熟时,该子群体的趋同过程结束; (3) 异化操作:各个优胜子种群和临时子种群趋同操作完成后,便执行异化操作。在整个解空间中,各子群体为成为胜者而竞争,不断的探测解空间中心点,此过程称为异化; (4) 判断是否满足终止条件:满足迭代停止条件时,算法结束优化过程,否则返回步骤(2); (5) 输出最优解:据编码规则,对寻找到的最优个体进行解析,输出最优解。 考虑到对电池性能的影响,充电策略要保证充电时间的连续性。将一天连续时间离散化为96个时间段。电动汽车用户接入充电枪后,充电桩记录电动汽车接入时间Ts,并从该车的电池管理系统获取B、S0等信息,由用户手动输入TL、St等信息。其中Ts∈(1,2,...,96),S0∈(0,1),St∈(0,1)。 实际上,利用MEA算法对电动汽车进行有序充电,就是在满足约束条件的基础上,找出最佳的充电开始时间Tb(Ts≤Tb≤(Ts+TL-Tg)),使得目标函数最优。文中采用MEA算法以充电开始时间后移的段数为目标函数的解。充电开始时间后移的段数确定之后,充电开始时间也就随之确定。MEA算法中的每个个体代表一个后移的时间段数,即一个可行解。经过MEA算法的趋同和异化操作,可以找到使目标函数最优的可行解,即Tb。如果用户响应有序充电,则在下一时间段更新充电站系统状态,并且等待到Tb再进行充电;如果用户不响应有序充电,从下一时间段开始更新充电站系统状态,并且开始充电,按照峰值电价进行计价。但由于约束条件的限制,会出现MEA算法无解的异常情况。 为验证基于MEA算法的有序充电控制策略的有效性,以北京市某电动汽车充电站为例进行仿真分析。由于目前电动汽车的充电费用和服务费用尚无统一标准,因此设置充电高峰电价cf为1.509 6元/(kW·h),低谷电价cg为充电高峰电价的一半,即0.754 8元/ (kW·h)[14]。 表1为该充电站的充电需求调研情况,采用蒙特卡洛算法模拟600辆电动汽车充电日需求数据;MEA算法中设置种群大小s为100,优胜子种群b和临时子种群t分别为5,迭代次数imax为30。利用MATLAB编程实现电动汽车的有序充电控制。 表1 电动汽车充电参数Table 1 Charging parameters of electric vehicles 不同用户响应度下充电站电动汽车充电负荷曲线如图3所示。可以看出,用户响应度越高,负荷转移效果越明显。有序充电下,当只有20%的用户响应时,充电站负荷转移效果较差;当有50%的用户响应时,负荷转移效果一般;当有90% 用户响应时,负荷转移效果较好。即用户响应度越高,系统的削峰填谷效果越明显。 图3 不同用户响应度下负荷曲线对比Fig.3 Load curves underdifferent customer participation probability 现采用遗传算法(GA)对电动汽车充电时间进行寻优,实现有序充电控制。GA算法的参数设置如下: 种群大小为100,迭代次数为30。比较GA与MEA两种算法下不同用户响应度时的负荷峰谷差,结果如表2所示。可以看出,响应度相同时,与GA算法相比,采用MEA算法时日负荷峰谷差较小,削峰填谷效果更好。 表2 不同响应度下负荷峰谷差对比Table 2 Comparation of maximum peak to valley difference under different customer participation probability kW 图4为基于两种算法得到的不同响应度下一天内电动汽车用户总充电费用对比图。可以看出,有序充电可降低用户充电费用,且响应度越高,用户充电花费越低。与无序充电相比,响应度为90%时,用户充电费用降低较多;响应度为20%时,用户充电费用降低较少。响应度相同时,与GA算法相比,采用MEA算法能使用户充电费用更低,即MEA算法比GA算法更能有效降低用户充电费用。 图4 不同用户响应度下用户充电费用对比Fig.4 Comparation of charging fees of users under different customer participation probability 文中以电动汽车的充电需求和充电站的功率限制为约束条件,以用户充电费用最少和充电站负荷峰谷差最小为目标,提出了基于MEA算法的充电站有序控制策略。采用MEA算法对模型进行优化计算,并比较了采用MEA与GA两种算法下的负荷峰谷差与用户充电费用,结论如下:(1) 基于MEA算法的有序充电控制策略,在满足客户充电需求基础上,可以实现电动汽车充电负荷转移,提高充电站运行的稳定性,减少用户充电费用;(2) 与GA算法相比,相同用户响应度时,采用MEA算法的日负荷峰谷差更小,用户充电费用更少。 [1] 张洪财, 胡泽春, 宋永华,等. 考虑时空分布的电动汽车充电负荷预测方法[J]. 电力系统自动化, 2014, 38(1):13-20. ZHANG Hongcai, HU Zechun, SONG Yonghua, et al. Forecasting method of electric vehicle charging load considering time and space distribution [J]. Automation of Electric Power Systems, 2014, 38 (1): 13-20. [2] 沈珑桓, 宋国兵. 电动汽车电池更换服务收费标准研究[J]. 江苏电机工程, 2013, 32(3):26-29. SHEN Longhuan, SONG Guobing. Research on toll standard of electric vehicles battery swap service[J]. Jiangsu Electrical Engineering, 2013, 32(3):26-29. [3] 俞豪君, 梁 茜, 许文超,等. 慢充和换电方式下的电动汽车充电负荷计算[J]. 江苏电机工程, 2015, 34(2):58-61. YU Haojun, LIANG Qian, XU Wenchao, et al. Charging load calculation of electric vehicles under normal charging mode and battery exchange mode[J]. Jiangsu Electrical Engineering, 2015, 34(2):58-61. [4] 郭小强, 李 建, 王宝诚,等. 微电网暂态故障时电动汽车充电器动态行为研究[J]. 电器与能效管理技术, 2017(3):78-83. GUO Xiaoqiang, LI Jian, WANG Baocheng, et al. Research on dynamic behavior of electric vehicle charger in transient fault of microgrid[J]. Low Voltage Apparatus, 2017(3):78-83. [5] 涂轶昀, 李 灿, 承 林,等. 电动汽车接入电网及其对电力系统的影响[J]. 华东电力, 2011,39(7):1085-1088. TU Yiyun, LI Can, CHENG Lin, et al. Vehicle-to-grid technology and its impact on power system[J]. East China Electric Power, 2011,39(7):1085-1088. [6] 孙建龙, 李 妍, 胡国伟,等. 电动汽车接入对配电变压器使用寿命的影响[J]. 高电压技术, 2015, 41(11):3830-3835. SUN Jianlong, LI Yan, HU Guowei,et al. Influence of electric vehicle access on service life of distribution transformer[J]. High Voltage Engineering, 2015, 41(11):3830-3835. [7] 蔡亚楠. 电动汽车规模化充电对配电变压器寿命的影响分析[D]. 重庆大学, 2016. CAI Yanan. Analysis of influence of large-scale electric vehicle charging on life of distribution transformer[D]. Chongqing University,2016. [8] 吴 凯, 程启明, 白园飞,等. 电动汽车充电机的谐波分析与治理[J]. 电源技术, 2014, 38(9):1720-1722. WU Kai, CHENG Qiming, BAI Yuanfei. et al. Harmonic analysis and control of electric vehicle charger[J]. Chinese Journal of Power Sources, 2014, 38(9):1720-1722. [9] 陈奇芳, 刘 念, 陈 征,等. 考虑充电需求与随机事件的光伏充电站实时运行策略[J]. 电工技术学报, 2016, 31(18):142-150. CHEN Qifang, LIU Nian, CHEN Zheng, et al. Real-time operation strategy for PV-Based EV charging station considering charging demand and random events[J]. Transactions of China Electrotechnical Society, 2016, 31(18):142-150. [10] 占恺峤,宋永华,胡泽春,等. 以降损为目的的电动汽车有序充电优化[J].中国电机工程学报,2012,32(31):11-18. ZHAN Kaiqiao, SONG Yonghua, HU Zechun, et al. Coordination of electric vehicle charging to minimizea ctive power losses [J].Proceedings of the CSEE,2012,32(31):11-18. [11] 罗卓伟,胡泽春,宋永华,等. 换电模式下电动汽车电池充电负荷建模与有序充电研究[J].中国电机工程学报,2012,32(31):1-10. LUO Zhuowei,HU Zechun,SONG Yonghua,et al.Study on charging load modeling and coordinated charging of electric vehicles under battery swapping modes [J]. Proceedings of the CSEE , 2012 , 32(31): 1-12. [12] 胡海彬. 电动汽车充电站功率控制策略研究[D]. 电子科技大学, 2011. HU Haibin. Research on power control strategy of electric vehicles in charging station [D]. University of Electronic Science and Technology of China, 2011. [13] SORTOMME E, HINDI M M, MACPHERSON S D J, et al. Coordinated charging of plug-in hybrid electric vehicles to minimize distribution system losses[J]. IEEE Transactions on Smart Grid, 2011, 2(1):198-205. [14] 徐智威, 胡泽春, 宋永华,等. 基于动态分时电价的电动汽车充电站有序充电策略[J]. 中国电机工程学报, 2014, 34(22):3638-3646. XU Zhiwei, HU Zechun, SONG Yonghua,et al. Coordinated charging of electric vehicles in charging station[J]. Proceedings of the CSEE, 2014, 34(22): 3638-3646. [15] 葛少云,郭建祎,刘 洪, 等. 计及需求侧响应及区域风光出力的电动汽车有序充电对电网负荷曲线的影响[J]. 电网技术,2014,38(7): 1806-1811. GE Shaoyun, GUO Jianyi, LIU Hong, et al. Considering the demand response and regional landscape output orderly charging of electric vehicle impact on the load curve of power grid [J]. Power System Technology, 2014,38(7):1806-1811. [16]艾格林, 孙永辉, 卫志农,等. 基于MEA-Elman神经网络的光伏发电功率短期预测[J]. 电网与清洁能源, 2016, 32(4):119-125. AI Geling,SUN Yonghui, WEI Zhinong, et al. Photovoltaic power prediction MEA-Elman neural network based on short-term[J]. Power System and Clean Energy, 2016, 32 (4): 119-125. [17] LIU H, TIAN H, LIANG X, et al. New wind speed forecasting approaches using fast ensemble empirical model decomposition, genetic algorithm, mind evolutionary algorithm and artificial neural networks[J]. Renewable Energy, 2015, 83:1066-1075. 余晓玲 余晓玲(1995—),女,青海海东人,工学硕士,研究方向为新能源发电控制技术、储能系统性能评估等(E-mail:ldyzyxl@163 .com); 余晓婷(1997—),女,青海海东人,工科学士,研究方向为电气工程及其自动化、大规模储能技术(E-mail:ldyzyxl@126.com); 韩晓娟(1970—),女,吉林吉林人,教授,研究方向为新能源发电控制技术、储能系统性能评估等(E-mail: wmhxj@163.com)。 (编辑方 晶) ACoordinatedChargingStrategyforPEVChargingStationsBasedonMindEvolutionaryAlgorithm YU Xiaoling1, YU Xiaoting2, HAN Xiaojuan1 (1. School of Control and Computer Engineering, North China Electric Power University, Beijing 102206, China;2. School of Water Conservancy and Electric Power, Qinghai University, Xining 810016, China) A large number of electri c vehicles connected to charging stations will increase the peak-valley difference and affect the safe and stable operation of the electric vehicle charging stations. Thus a coordinated charging strategy for plug-in electric vehicle (PEV) charging stations based on Mind Evolutionary Algorithm (MEA) is proposed. The strategy set minimum customer charging costs and minimum peak-valley difference as objective function. The optimal charging period of electric vehicles is calculated dynamically by using MEA. Customers decide whether or not to respond to peak-valley prices and to delay their charging to lower price periods by themselves. The charging coordination of electric vehicles is then realized. In order to verify the effectiveness of the proposed strategy, the Monte Carlo simulation method was utilized to generate the charging needs of customers based on actual customer charging behaviors. The distribution transformer load profiles, customer charging costs were simulated under uncoordinated and coordinated charging scenarios correspondingly. Simulation results indicate that under the proposed coordinated charging control strategy, customer charging costs can be greatly reduced and the peak shaving of distribution transformer loading profile can also be achieved; compared with genetic algorithm, the effect of MEA is better. plug-in electric vehicle (PEV) charge station; Monte Carlo simulation; MEA; coordinated charging strategy;peak and valley electric charges TM73 A 2096-3203(2017)06-0058-05 2017-07-10; 2017-08-07 国家自然科学基金资助项目 (51577065)2 优化模型
2.1 目标函数
2.2 约束条件
3 基于MEA算法的充电时间寻优
3.1 MEA算法
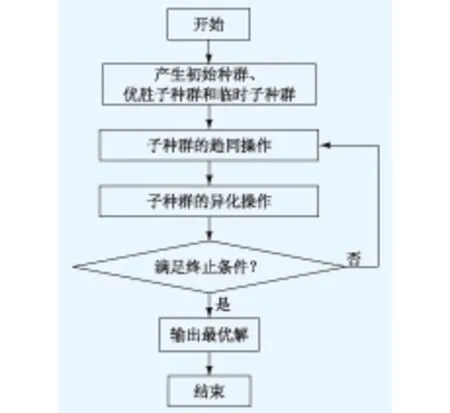
3.2 基于MEA算法的充电时间寻优
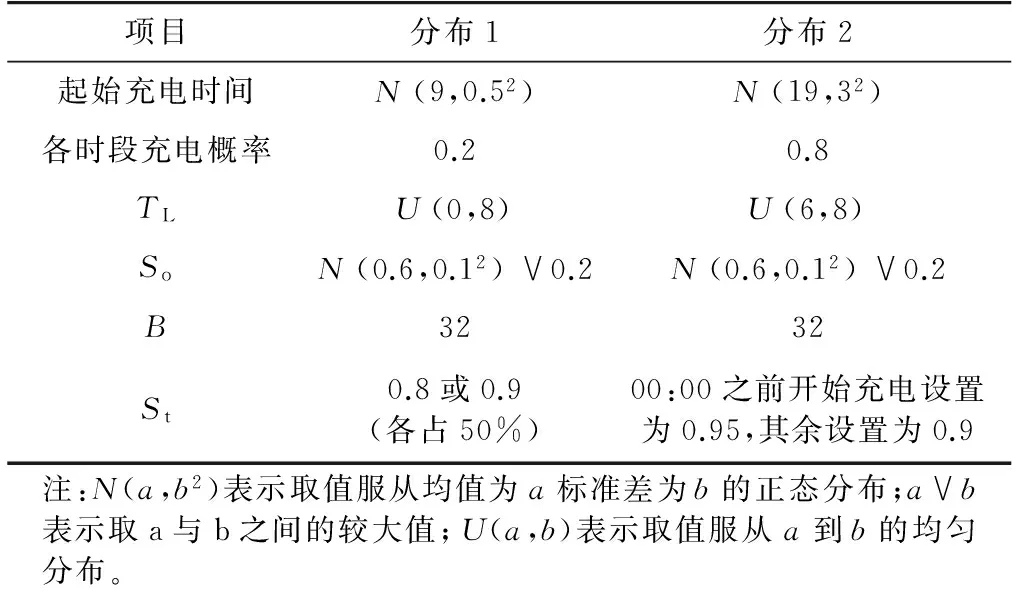
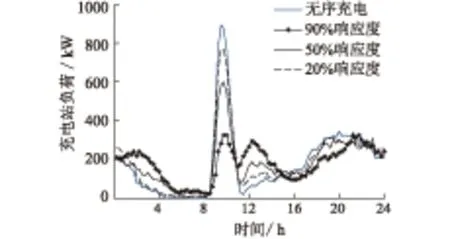
4 算例仿真
5 结语


