电动汽车充电站多阶段选址规划

陈梦涛， 张兆君， 谭风雷，史贤悦， 王 杰， 韩华春

(1. 国网江苏省电力公司检修分公司， 江苏 南京 211102；2. 江苏省电力公司电力科学研究院，江苏 南京 211103)

电动汽车充电站多阶段选址规划

陈梦涛1， 张兆君1， 谭风雷1，史贤悦1， 王 杰1， 韩华春2

(1. 国网江苏省电力公司检修分公司， 江苏 南京 211102；2. 江苏省电力公司电力科学研究院，江苏 南京 211103)

电动汽车充电站作为电动汽车运营所需的配套设施，其建设时间、位置与规模对电动汽车的推广有着重要意义。现有研究将电动汽车充电站的规划选址作为一个静态规划问题处理，忽视了电动汽车充电站的建设时间，因此提出了一种电动汽车充电站选址的多阶段规划模型，并应用伪动态规划的思想求解该模型。首先提出了一种计及电动汽车充电站投资成本、运行维护成本以及用户充电损耗费用的多阶段规划模型；其次在准确预测各阶段充电需求的基础上，通过遗传算法确定规划期末的规划方案；最后通过动态规划逆序解法获得各阶段的规划方案，算例分析验证该方案的优越性。

充电站选址; 多阶段; 遗传算法; 动态规划

0 引言

随着全球能源危机的加深和环境的持续恶化，电动汽车作为低污染、零排放的交通工具越来越受到大家的青睐。电动汽车充电站作为电动汽车的重要基础设施，对电动汽车的发展起着至关重要的推动作用。针对电动汽车充电站的选址、定容规划，国内外学者进行了大量的研究。文献[1]综合考虑建设成本和用户充电成本，提出了一个多等级充电站的规划模型，并通过改进的禁忌搜索算法实现了站址、站容的优选；文献[2]综合考虑充电站作为普通用电设施和公共服务设施的特性，通过建立多目标规划模型，完成充电站的最优选址；文献[3]通过粒子群算法和加权伏罗诺伊图实现了充电站选址定容和服务区域划分的最优；文献[4]提出了计及充电站服务半径和地理因素的两步筛选法，建立了规划期内充电站建设总成本和网损费用之和最小的目标函数，通过改进的原对偶内点法，实现了充电站选址问题的最优。

文献[1-5]将充电站规划选址作为静态规划处理，而充电站作为重要基础设施，其建设时间和规模应遵循与城镇发展相协调，结合现有电动汽车充电需求，并适当超前的原则[6-10]。因此从本质而言充电站的选址规划是一个多阶段，多变量的规划问题。动态规划算法[11-15]是解决多阶段问题的经典算法，但随着优化规模和维数的增大，动态规划算法容易出现“组合爆炸”和“维数灾”问题。为此文中采用伪动态规划的思想，通过遗传算法(GA)计算出规划期末的最优规划方案，将优化变为固定始端和终端的多阶段规划问题，通过动态规划逆序算法轻松算出各个规划阶段的充电站建设方案。

1 多阶段充电站规划的数学模型

1．1 模型假设

(1) 充电站的候选点都是经过一定的分析和论证得到的，考虑了需求点及需求量的分布，符合充电站的选址原则、环境条件和安全条件；

(2) 每个需求点代表一个小型区域，相应需求点处的需求量指该小型区域内有充电需求的电动汽车总数量[7]；

(3) 每个需求点处的所有电动汽车用户，在一个固定的时间段内只能到同一个充电站接受充电服务；

(4) 用户的充电成本与距离呈简单线性关系，且距离为欧氏距离；

(5) 已建成的充电站不可拆除，只能在原有基础上扩建或保持原样。

1．2 目标函数

综合考虑各阶段充电站的投资成本、运行维护成本以及用户的充电损耗费用，以各阶段的综合成本之和最小为目标建立模型。

(1)

式中：N为规划阶段数；CT(k)为阶段k的投资成本；CS(k)为阶段k的运行维护成本；CY(k)为阶段k用户的充电成本。

(2)

(3)

(4)

式中：n为目标年充电站个数；Si(k)为第i号充电站在阶段k的容量；f(Si,k)为第i号充电站在第k阶段的投资费用(计及土地费用)；u(Si,k)为第i号充电站在阶段k的年运行维护费用；Ji(k)为第i号充电站在阶段k所供负荷点的集合；y(k)为阶段k的起始年份数；r为贴现率；t为道路曲折系数；η为道路畅通系数；ω为每辆车的平均充电次数；z为折返系数；gij为第j号需求点是否到第i号充电站充电的参数；l为单位折损系数；dij为第i个充电站到第j个充电需求点的距离。

1.3 每个阶段的约束条件

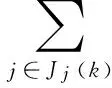
(5)

dij≤Ri(i=1,…,n,j∈Ji(k))

(6)

(7)

Si(k)∈{0,1,2,3,4}

(8)

式中：k为第k阶段；Wj(k)为第j号充电需求点在第k阶段的充电需求预测值；e(Si(k))为第i号充电站在阶段k的运行率；cosφ为功率因数；Ri为第i个充电站的充电半径。其中式(5)表示充电站需满足的容量约束；式(6)表示充电站的充电半径约束；式(7)表示每个充电需求点能且只能到一个充电站充电；式(8)表示充电站的等级约束。

1．4 目标函数

Si(k)≤Si(k+1)

(9)

式(9)表示下一阶段的容量需建立在上一阶段的基础上。

动态规划是解决多阶段问题的经典方法。其基本思想是将所给问题全过程分解成若干个互相联系的阶段，给出每个阶段所处的自然状况或客观条件，即确定每个阶段的状态；然后寻找出各个阶段(除最后一个阶段)每个状态到下个阶段每个状态的所有可行转移路径即允许决策集合；并据此得到全过程的一个最优状态转移路径，称为最优策略，确定整个过程的优化结果。但随着优化规模和维数的增大，动态规划方法容易出现“组合爆炸”和“维数灾”问题，同时充电站建设方案具有不可逆性。因此文中采用伪动态规划的思想，即在准确预测各阶段充电需求的基础上，通过GA算法计算出规划期末的最优规划方案，其他各阶段规划方案都必需以此为约束条件，至此优化问题变为固定始端和终端的多阶段规划问题，通过动态规划逆序算法可以计算得到各个规划阶段的充电站建设方案，如图1所示。

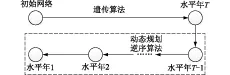
图1 充电站多阶段选址规划Fig．1 The multi-stage planning model of the charging station’s location

2 遗传算法求解规划期末的规划方案

规划期末的规划方案就是在预测规划期末充电需求的基础上，从给定的备选站址中选出本阶段的最优规划，属于静态组合优化问题，而GA算法适用于求解大规模的组合优化，故文中通过GA算法求解最终的规划方案。

2．1 染色体编码

编码策略直接影响个体被GA算子操作时的变形特性以及个体解码时从基因型空间到表现型空间的映射性质。对于事先给定待选站址的充电站规划方法，一般使用传统的二进制编码，即由二进制符号0和1表示当前待选站是否被选中。文中为了同时计算出站址和站容而采用十进制编码，选址变量Xi∈{0,1,2,3,4}，Xi=0表示不在i处建设充电站；Xi=1表示在i处建设等级1的充电站；Xi=2 表示在i处建设等级2的充电站；Xi=3表示在i处建设等级3的充电站；Xi=4表示在i处建设等级4的充电站。根据文中编码方法可知编码长度为I(备选站址的个数)，非零染色体的个数为P(P≤M，M为规划充电站的个数)。

文中编码仅确定了充电站的站址和站容，并未涉及各充电负荷的分配问题，因此设计如下“聚类”操作，完成充电需求的分配：针对不同的n，根据染色体的编码，按照就近原则把充电负荷分配到各个充电站；当距离某个充电负荷最近的充电站容量达到该充电站编码表示的容量上限时，则将该充电负荷分配到次近的充电站，直到分配结束。

3 动态规划逆序算法求解各阶段规划方案

经第一阶段的GA算法计算出规划期末的最优规划方案，使优化问题变为如图2所示的固定始端和终端的多阶段规划问题，通过动态规划逆序算法可以计算出各个规划阶段的充电站建设方案。

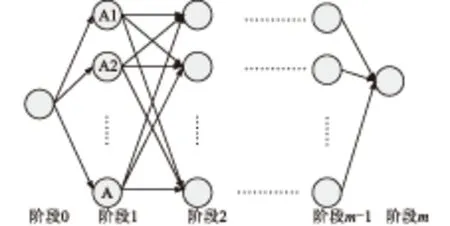
图2 状态转移Fig． 2 State transition diagram

4 实例分析

文中以某市某开发区的充电站选址定容为例：该开发区总面积30 km2，东西长5 km，南北长6 km，开发区内可等效为30个充电需求点。部分需求点的位置和各阶段的充电需求预测量如表1所示；通过专家评议获得的10个充电站候选点位置如表2所示；参照北京市出台的标准文件“电动汽车电能供给与保障技术规范：充电站”，规定4种等级的充电站相应的服务能力及建设成本如表3所示。假设充电站经济使用年限为20年；各规划阶段的间隔年份为5年；规划的目的是从10个候选站址中选择5个站点建设充电站，并规划出各阶段充电站的建设方案。

表1 部分需求点位置及对应需求量Table 1 Partial demand points location and corresponding demands

表2 候选点的位置Table 2 candidate points coordinate km

表3 充电站的等级及相应建设成本Table 3 Station levels and corresponding construction costs

根据以上算法，利用Matlab7.1进行编程，其中参数设置为：种群规模为50，迭代次数为300。对该假设算例独立运行20次，得出规划期末的规划方案：选择在备选站址2、5、7、8、9分别建立等级为3、4、1、1、3充电站，通过动态规划逆序算法求得各阶段的规划方案如表4所示，各阶段建站位置及需求点的分配如图3—6所示。

表4 各阶段规划方案Table 4 Planning at various stages

图3 阶段1充电负荷分配Fig． 3 The first stage of allocation of burden

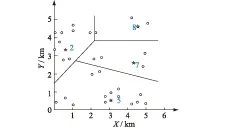
图4 阶段2充电负荷分配Fig． 4 The second stage of allocation of burden

图5 阶段3充电负荷分配Fig． 5 The third stage of allocation of burden

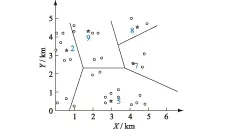
图6 阶段4充电负荷分配Fig． 6 The fourth stage of allocation of burden

分析以上结果得：在初始阶段，由于电动汽车充电需求较少，充电站的建设费用在总费用中占据较大的部分，因此初始阶段充电站建设较少，充电负荷分配不均匀，充电站并不完全处于负荷重心处；随着充电负荷增加，用户的充电成本占总成本比例增大，此时各个充电站逐步趋向于其所分配负荷重心处，各充电站的负荷分配更加均衡合理。通过充电站的多阶段选址规划，使各阶段充电站的建设方案与本阶段电动汽车充电负荷的发展情况相匹配，在充分考虑各阶段充电便利性的基础上减少了充电站建设的初始投资，为充电站的循序建设提供了依据。

5 结语

文中建立了充电站多阶段规划数学模型，采用伪动态规划思想求出了整个规划期间的最优充电站建设方案，并通过实际算例验证了该方案的有效性。该方案对相关充电站建设实践具有一定的参考价值，但对各阶段充电需求的准确预测有较大依赖性，因此未来如何准确预测各阶段的充电需求将是该方案的进一步改进方向。

[1] 张国亮，李 波，王运发． 多等级电动汽车充电站的选址与算法[J]． 山东大学学报(工学版)，2011，41(6)：136-142.

ZHANG Guoliang，LI Bo，WANG Yunfa． Location and algorithm of multi class electric vehicle charging station[J]．Journal of Shandong University(Engineering Science)，2011,41(6)：136-142.

[2] 刘志鹏，文福拴，薛禹胜，等． 电动汽车充电站的最优选址和定容[J]． 电力系统自动化，2012，36(3)：54-59.

LIU Zhipeng，WEN Fushuan，XUE Yusheng，et al． The optimal siting and sizing of automation[J]． Automation of Electric Power Systems，2012，36(3)：54-59.

[3] 唐现刚，刘俊勇，刘友波，等． 基于计算几何方法的电动汽车充电站规划[J]． 电力系统自动化，2012，36(8)：24-30.

TANG Xiangang，LIU Junyong，LIU Youbo，et al． Planning of electric vehicle charging station based on computational geometry method [J]．Automation of Electric Power Systems，2012，36(8)：24-30.

[4] 王 辉，王贵斌，赵俊华，等． 考虑交通网络流量的电动汽车充电站规划[J]． 电力系统自动化，2013，37(13)：63-69.

WANG Hui，WANG Guibin，ZHAO Junhua，et al． Considering the station planning automation[J]．Automation of Electric Power Systems ，2013，37(13)：63-69.

[5] 刘自发，张 伟，王泽黎． 基于量子粒子群优化算法的城市电动汽车充电站优化布局[J]． 中国电机工程学报，2012(22)：39-45.

LIU Zifa，ZHANG Wei，WANG Zeli． Optimal layout of urban electric vehicle charging station based on quantum particle swarm optimization[J]． Proceedings of the CSEE，2012(22)：39-45.

[6] 杨永标，黄 莉，徐石明，等． 电动汽车换电商业模式探讨[J]． 江苏电机工程，2015，34(3)：19-24.

YANG Yongbiao，HUANG Li，XU Shiming，et al． Discussion on the electric business model of electric vehicles [J]． Jiangsu Eelectric Engineering，2015，34(3)：19-24．

[7] 俞豪君，梁 茜，许文超，等． 慢充和换电方式下的电动汽车充电负荷计算[J]． 江苏电机工程，2015，34(2)：58-61.

YU Haojun， LIU Qian， XU Wenchao，et al． Charge load calculation of electric vehicle under slow charge and switching mode[J]． Jiangsu Electric Engineering，2015，34(2)：58-61.

[8] 薛钟兵，彭 程． 新能源发电与电动汽车充换储站协调运行研究[J]． 江苏电机工程，2014，33(5)：36-38.

XUE Zhongbing，PENG Cheng． Study on coordinated operation of new energy power generation and electric vehicle replacement storage station[J]． Jiangsu Electric Engineering，2014，33(5)：36-38.

[9]沈珑桓，宋国兵． 电动汽车电池更换服务收费标准研究[J]． 江苏电机工程，2013，32(3)：26-29.

SHEN Longhuan，SONG Guobin． Research on charge standard for battery replacement service of electric vehicles[J]．Jiangsu Electric Engineering，2013，33 (3)：26-29.

[10] 李 斌，刘 畅，陈企楚，等． 电动汽车无线充电技术[J]． 江苏电机工程，2013，32(1)：81-84.

LI Bin，LIU Chang，CHEN Qichu，et al． Wireless charging technology for electric vehicles[J]．Jiangsu Electric Engineering，2013，32(1)：81-84.

[11] 杨 超，张步涵，陶 芬,等． 电力系统多时段无功电压控制的两阶段优化法[J]． 高电压技术，2007，33(9)：104-109.

YANG Chao，ZHANG Buhan，TAO Fen，et al． Two stage optimization method for multi period reactive power and voltage control[J]． High Voltage Technology，2007，33(9)：104-109.

[12] 王成山，康晓莉，余贻鑫. 城市高中压电网无功优化规划[C]∥ 中国电机工程学会城市供电学术年会论文集，1998：160-163.

WANG Chenshan, KANG Xiaoli, YU Yixin. Reactive power optimization planning of urban high voltage power network[C]∥ Proceedings of the Symposium on Urban Power Supply of Chinese Society of Electrical Engineering，1998：160-163.

[13] 葛少云，贾鸥莎． 配电充电站多阶段优化规划模型[J]． 电网技术，2012，36(10)：113-118.

GE Shaoyun，JIA Ousha．Multi-stage optimization planning model of distribution charging station[J]． Power System Technology, 2012，36(10)：113-118.

[14] 高炜欣，罗先觉． 基于Hopfield神经网络的多阶段配电变电站的规划优化[J]． 电工技术学报，2005，20(5)：58-64.

GAO Weixin，LUO Xianjue． Planning optimization of multi-phase distribution substations based on Hopfield neural network[J]．Transactions of China Electrotechnical Society，2005，20(5)：58-64.

[15] 王成山，唐晓莉，余贻鑫,等． 城市高中压电网无功功率优化规划[J]． 电网技术，1998，22(8)：23-26.

WANG Chengshan，TANG Xiaoli，YU Yixin，et al． Optimal planning of reactive power for urban high voltage power network [J]． Power System Technology，1998，22(8)：23-26.

陈梦涛

陈梦涛(1989—)，男，河南南阳人，硕士，工程师，从事电力系统继电保护、特高压运检技术工作(E-mail：1247788093@qq．com)；

张兆君(1977—)，男，江苏南京人，技师，从事特高压变电站专业设备管理工作；

谭风雷(1989—)，男，重庆万州人，硕士，从事特高压电网变电运行维护的工作；

史贤悦(1991—)，女，江苏盱眙人，本科，助理工程师，从事特高压运检技术工作；

王 杰(1991—)，男，江苏盱眙人，本科，助理工程师，从事特高压运检技术工作；

韩华春(1988—)，女，山东济宁人，博士，从事电动汽车V2G技术、新能源并网技术研究。

(编辑方 晶)

Multi-stageLocationPlanningofElectricVehicleChargingStation

CHEN Mengtao1, ZHANG Zhaojun1, TAN Fenglei1, SHI Xianyue1, WANG Jie1, HAN Huachun2

(1. State Grid Jiangsu Electric Power Maintenance Branch Company, Nanjing 211102, China;2. State Grid Jiangsu Electric Power Company Research Institute, Nanjing 211103, China)

As the necessary supporting facilities for electric vehicle operation, the construction time, location and scale of electric car charging stations are of great significance to the promotion of electric vehicles. The existing research takes the location planning of electric car charging stations as a static problem, ignoring construction time. Therefore, a multi-stage planning model of charging station location is proposed, and the model is solved by the idea of pseudo-dynamic planning. Firstly, a multi-stage programming model is proposed, which takes into account the investment cost, operation and maintenance cost and user charge loss expense. Secondly, based on the accurate prediction of the charging needs of each stage, the genetic algorithm is used to determine the planning scheme at the end of the planning period. Finally, the planning scheme of each stage is obtained by dynamic planning reverse solution. A case study proves the superiority of the scheme.

charging station location; multi-stage; genetic algorithm; dynamic planning

U469．72

A

2096-3203(2017)06-0117-05

2017-07-11；

2017-08-03

江苏省科技支撑计划项目资助(BE2014023)