高寒区多口融冰井引水渠道水温变化三维模拟及井群优化布置
吴素杰,宗全利※,郑铁刚,王子坚,刘贞姬
(1. 石河子大学水利建筑工程学院,石河子 832000;2. 中国水利水电科学研究院流域水循环模拟及调控国家重点实验室,北京 100038;3. 新疆兵团勘测设计院(集团)有限责任公司,石河子 832003)
高寒区多口融冰井引水渠道水温变化三维模拟及井群优化布置
吴素杰1,宗全利1※,郑铁刚2,王子坚3,刘贞姬1
(1. 石河子大学水利建筑工程学院,石河子 832000;2. 中国水利水电科学研究院流域水循环模拟及调控国家重点实验室,北京 100038;3. 新疆兵团勘测设计院(集团)有限责任公司,石河子 832003)
为探讨抽水融冰技术解决严寒地区渠道冰害的效果,以新疆玛纳斯河流域红山嘴二级电站引水渠道为研究对象,对多口融冰井同时运行条件下引水渠道水温变化过程进行三维模拟,其模拟结果和原型观测结果平均相对误差为4.61%,验证了数值模拟的可靠性。在此基础上,通过改变井水流量、井前渠水流量和水温、外界大气温度等条件,对混合水温沿程变化过程进行了模拟。结果表明:1)仅将井水流量变为原来的50%和1.5倍时,井水注入量与混合水温成正比,且对混合水温的影响较大;2)仅将井前渠道水温分别降低和升高0.2和0.4 ℃时,井前渠道水温与混合水温成正比,且对混合水温的影响也较大,因此增大井水流量或者合理布置井群是抽水融冰最有效的方法;3)根据井前渠道水温为0.1 ℃,井前渠水流量分别为10、15、20和25 m3/s,大气温度分别为–5、–10、–20和–30 ℃的模拟结果,得到了各井的不冻长度值,且随着井前渠道流量增大和外界大气温度降低,融冰井的不冻长度均随之减小,最后给出了在不同井前渠道流量和不同气温条件下融冰井的不冻长度和井的布置桩号等合理优化布置方案,此研究为解决寒区水电站引水渠道冰灾防治问题提供科学依据。
温度;井群;优化;引水渠道;抽水融冰;数值模拟;不冻长度
0 引 言
在中国,引水式电站为了获得一定的发电水头,通常会修建长距离的引水渠道。而由于冬季严寒且冰期漫长,渠道内冰的形成与消融以及可能带来的危害是引水式电站冬季正常运行必须考虑的关键因素[1]。实践证明,在寒冷地区,采用抽水融冰这种外界能量汇入引水渠道以提升水温的方法来解决水电站冬季运行冰害,是一项经济安全可行的技术措施。
目前国内外针对引入外界能量以提升渠道水温的方法直接研究成果很少,仅在中国有少数水电站采用该方法,并有部分研究。早期邓朝彬、王文学等对香加水电站和金沟河电站引水渠道应用外界能量汇入渠道运行发电实践经验进行了介绍[2-3];近几年刘新鹏等[4-6]对红山嘴电站应用外界能量汇入以提升水温的技术原理、效益等进行了研究,计算了融冰井的不冻长度,并研究了融冰井群应用。
随着计算流体力学以及计算机软硬件的快速发展,直接建立紊流数学模型对引水式电站引水渠进行数值模拟已成为可能。但目前相关数值模拟主要集中在河渠内冰水变化规律等方面。例如高霈生等[7-12]均采用数值模拟的方法分析了河道、干渠沿程的水温变化,及水中冰的形成分布等规律;陈明千等[1,13]通过建立冰花消融数学模型,模拟研究了水内冰花的密度随时间和空间变化的过程;陈武等[14]用其建立的三维流固耦合传热数学模型,预测分析了封闭式渡槽的水温变化;王晓玲等[15-16]基于三维非定常流Eulerian- multiphase模型,研究了渠道引水温度以及渠水流速在不同引水流量、不同气温工况下水内冰体积分数的沿程分布规律。
前苏联和瑞典曾分别对引水式电站进行了长期的原型观测试验[17],研究了冰盖底部的形状及其温度变化规律,提出的预防及消除冰灾的措施现今仍然适用。Shen等[18]提出了RICEN 模型,该模型不仅可以模拟过冷现象和底部冰的形成,而且还加入了风、人工破冰和河冰水流阻力因素的影响;Liu等[19]通过建立的河冰模型,对圣劳伦斯河上游河段水内冰的形成及消融过程进行了模拟分析;Shen和Lu[20]利用二维河冰数学模型,对冰塞体的溃决过程进行了模拟;Jasekatal等[21]利用建立的冰下过流量模型,对道森市附近的育空河段进行了估算;Wang等[22]对过冷现象及冰凌形成发展过程进行了模拟研究;Chen等[23]分别对表层浮冰、悬浮水内冰的水温及悬浮冰花浓度分布进行了模拟研究;Betchelor 和Wadia研究了水中冰花密度及其热力交换[24-25]。上述研究主要针对河、渠内冰形成演变过程,而抽水融冰是一种冰花消融的过程,与此恰好相反。
吴素杰等曾对单井运行条件下抽水融冰水温变化过程进行了模拟,得到了不同外界条件下,引水渠道水温沿程变化规律[26]。虽然单井模拟的水温变化规律结果在一定程度上代表了实际运行中水温的变化过程,且多口井同时运行时井水水温变化的耦合影响很小,但实际工程中融冰井都是多井同时运行,为了研究多井运行时井群的合理优化布置方案,更切合实际工程和更加准确地研究抽水融冰技术提升渠道水温的效果,本文利用FLUENT软件建立3D紊流数学模型,探讨该技术运行下引水渠道沿程水温变化规律,并在此基础上,得到不同参数条件下各井的不冻长度值,为引水式电站输水渠道冬季安全稳定工作提供理论依据及技术支持。
1 原型观测试验
为研究此外界能量汇入下引水渠道冬季实际运行效果及验证数学模型的可靠性,分别于2013年和2015年的2-3月,以新疆玛纳斯河流域的红山嘴二级电站引水渠道为研究对象,进行了引水渠道沿程水温的观测试验,图1为原型观测区域,图2为引水渠井水汇入现场。在整个观测过程中,外界气温均保持在0℃以下,且当时二级电站引水渠运行了7口融冰井,分别为5#井、6#井、8#井、9#井、10#井、11#井、13#井,剩余融冰井均未运行。受实际地理环境影响,水温观测试验采用塑料水壶多点多次取水,并用 2支校核过的水银温度计多次测量测取平均值的方法。
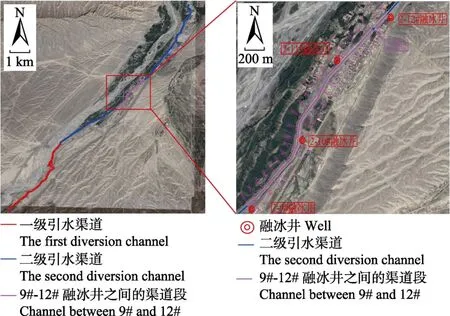
图1 红山嘴电站二级引水渠道原型观测区域Fig.1 Prototype observation area in second diversion channel of Hongshanzui Water Power Station

图2 红山嘴电站二级引水渠道抽水融冰现场Fig.2 Site of pumping well water to melt ice in second diversion channel of Hongshanzui Water Power Station
2 数学模型
2.1 控制方程
在自然水域中,密度是温度和压力的函数。在不可压缩流动中,忽略压力的影响,仅考虑温度对密度的影响,其关系近似表示为[27]:

式中ρ为流体的密度,kg/m3;T为温度,℃。
对于常态下水体,密度与温度的关系可表示为
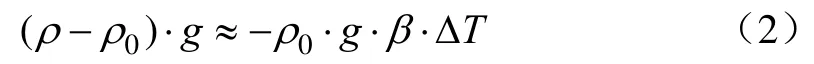
式中ρ0为参考温度下流体的密度,kg/m3;g为重力加速度,m/s2;β为热膨胀系数;TΔ为流体温度与参考状态温度的差值,℃。
Boussinesq的假设,针对密度变化微小的浮力流问题,所有方程中的密度恒定,仅考虑方程重力项中的密度变化,忽略控制方程中其余项的浮力作用。
连续性方程[28]:

式中t为时间,s;ui为i方向上的流速,m/s;xi为x轴在i方向上的分量;Sm为源项,是加入到连续相的质量,kg,源项也可以是任何的自定义源项。此方程为连续性方程的一般形式,可用于不可压流动和可压流动。
动量方程:
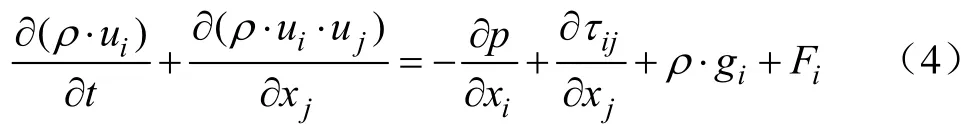
式中p为静压,Pa;uj为j方向上的流速,m/s;xj为x轴在j方向上的分量;gi和Fi分别为i方向上的重力体积力和外部体积力;Fi还包括了如自定义原项的其余模型的有关源项,m/s2;τij为应力张量,Pa,由下式给出[21]:

式中μ为动力黏性系数,N/(m·s);ul为l方向上的流速,m/s;xl为x轴在l方向上的分量;ijδ为kronecker符号。
能量方程:

式中k为流体的传热系数,W/(m·K);cp为比热容,J/(kg·K);ST为黏性耗散项,J/(kg·mol·K)。其中cp、k、ST在本文模拟过程中设置为液态水默认值常数,其值分别为cp=4 182J/(kg·K),k=0.6W/(m·K),ST=69 902.21J/(kg·mol·K)。
2.2 模型建立及网格生成
以新疆玛纳斯河流域红山嘴电站二级引水渠道为例,为探寻融冰井群运行过程中引水渠道沿程水温变化以及各井之间的耦合影响作用,选取最具代表性的 9#、10#、11#井(9#、10#、11#融冰井之间的距离分别为 800和850 m)上下游渠段建立引水渠三维紊流数学模型。模型取9#井前50 m处为渠道入口,12#井处为渠道混合水出口(由于原型观测时12#融冰井未运行,对12#井前混合水温不影响),且全部由出口流出;沿程9#、10#、11#井分别按照实际工程中的位置设置。实际中因较低的大气温度和积雪的层层覆盖,在融冰井注水管口处极易形成一个与封闭管道相似的冰体管道,使抽出的井水经管道直接由渠道水面注入渠道,因此数学模型中将井水注入口位置设置与渠道水面持平。
模型横断面为梯形,其底宽、边坡系数分别为1.0 m、1.75,由于实际工程中各井的流量仅占渠水流量的1.3%~2.4%,对渠道水深影响不大,所以模拟中水深与实际一样,取2.743 m。网格划分用FLUENT自带前处理软件GAMBIT进行,划分过程采用结构网格与非结构网格两种方法相结合,其网格单元总数为 178万,整个渠道主流方向网格单元尺寸是0.1m×5 m,水深和宽度方向均为0.1 m×0.1 m;因井水注入口上下游为计算的关键位置,为了保证计算的精度,故将井水注入口附近的网格划分较密,最小单元尺寸设置为 0.05 m×0.25 m×0.25 m,最大单元尺寸设置为0.10 m×0.10 m×0.10 m,网格局部见图3所示。

图3 数值计算网格局部示意图Fig.3 Schematic diagram of local grid of numerical simulation
2.3 求解方法和边界条件
2.3.1 求解方法
模拟采用有限体积法来离散计算区域,即用控制体积法求解定常流连续性方程和N-S方程,用标准k–ε紊流模型来连续和封闭动量方程;并选用SIMPLEC算法对压力和速度进行耦合求解。收敛标准:计算各变量残差设置为(<1e–06),或者残差曲线随迭代进行趋于平稳,即可认为计算收敛。
2.3.2 边界条件
渠道入口和各井水注入口设置为速度入口,其入口流速分别由原型观测资料给定,其紊流特征参数中紊流强度I和紊流长度尺度L分别由式(7)、(8)计算得出。
紊流强度[29]:

式中Re为雷诺数;v为流速,m/s;d为管径,m。
紊流长度尺度[29]:

式中A为截面积,m2;X为湿周,m。圆管的水力直径为圆管的直径。
因原型观测引水渠道为敞露渠道,且渠水流动为不可压缩流动,故将渠道的水流出口设置为自由出流边界。由于渠道水面波动较小,故采用“刚盖”假设模拟渠道自由水面,而渠道周围大气温度边界采用原型观测时实际大气温度。
渠道边壁设置为无滑移边界,壁面粗糙高度设置为2.1 mm。数学模型所需的边界条件均采用9#、10#、11#融冰井原型观测数据,见表1。

表1 红山嘴电站实测数据(2015年3月1日13时)Table 1 Measured data of Hongshanzui Water Power Station at 13:00 , on March 1st, 2015
3 结果与分析
3.1 数学模型验证
采用原型实测数据(表1)作为模拟的边界条件计算引水渠混合水温的沿程变化,提取融冰井一侧距离岸边0.18 m处水面(即原型观测时取水位置)沿程混合水温的数据,并与2015年3月1日红山嘴电站原型观测沿程水温数据进行对比验证,见图4。由图可知,模拟得到的渠道混合水温与原型观测所得渠道混合水温 2条曲线变化规律基本一致,吻合性较好,最大误差为8.93%,最小误差为0.03%,平均相对误差为4.61%,在允许范围内[30]。由此可知,本文采用的计算模型准确可靠,模拟结果可信。
3.2 渠水速度和温度模拟结果
以 9#井附近渠段为例,提取井水进水管平面沿程水温进行分析,速度云图可以清晰显示井水汇入处上下游水流的大小及其流动方向,且各方向速度模拟结果见图5。从图中可以看出,井水Y方向流速对渠水流速度影响较小,而井水X方向流速和Z方向流速相比对渠道水流速度影响较大,但渠水流速都仅在井水注入口附近有较小范围的变化,且充分混合后渠道水流方向大小又基本恢复注水前水流主流方向大小。
图6为9#井上下游渠段数值模拟的温度云图,图中井水注水管水温较高表现为红色,渠水温度较低表现为蓝色。从图6a~d中可以看出,在水深方向上离融冰井注水口越远,水温变化越不明显,而且在注水井后 250 m左右之后,上层水温因与外界大气温度直接接触有明显变化,特别是渠道水面变化最为显著,下层水温却无明显变化。从图6e主流方向上温度云图观察,因井前渠道流量远大于井水注入量,所以整个渠道水温的变化并不明显,仅在井水注入处附近有较大变化,但是计算结果显示,井水汇入渠道充分混合之后,渠水温度有明显升高。

图4 渠道混合水温模拟值与实测值对比Fig.4 Comparison between simulation and measured values of mixed channel water temperature
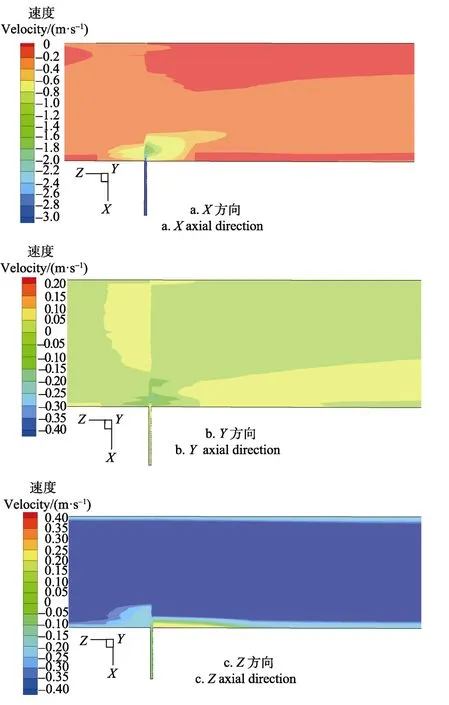
图5 9# 井上下游速度数值模拟结果Fig.5 Results of numerical simulation for velocity in upstream and downstream of No.9 well

图6 9#井上下游温度数值模拟结果Fig.6 Results of numerical simulation for temperature in upstream and downstream of No.9 well
3.3 不同边界条件下水温变化过程模拟
进一步对不同边界条件下引水渠道沿程水温的变化进行模拟,研究多个融冰井同时运行对渠道水体增温融冰效果的影响。在实际工程中,由于融冰井水温基本恒定,同时井前渠道流量变化对渠道混合后水温的影响也不明显[19],因此本文仅分析不同井水流量和不同井前渠道水温变化对渠道沿程水温的影响。
3.3.1 井水流量变化对渠道混合水温的影响
1)双井井水流量变化对渠道混合水温的影响
井前渠道流量、井前渠道水温保持不变(Q=10.57 m3/s、T=1.37 ℃),根据实际工程中各融冰井可能的出水流量,将本文中 9#、10#、11#融冰井的井水流量分别降低和升高为原来(0.18、0.13和0.16m3/s)的50%和1.5倍,模拟渠道融冰效果。由于主流方向上混合水温变化相比水深方向混合水温变化更能反映引水渠道沿程水温变化过程,所以模拟结果提取渠道水面沿程混合水温的平均值,结果如图7所示。
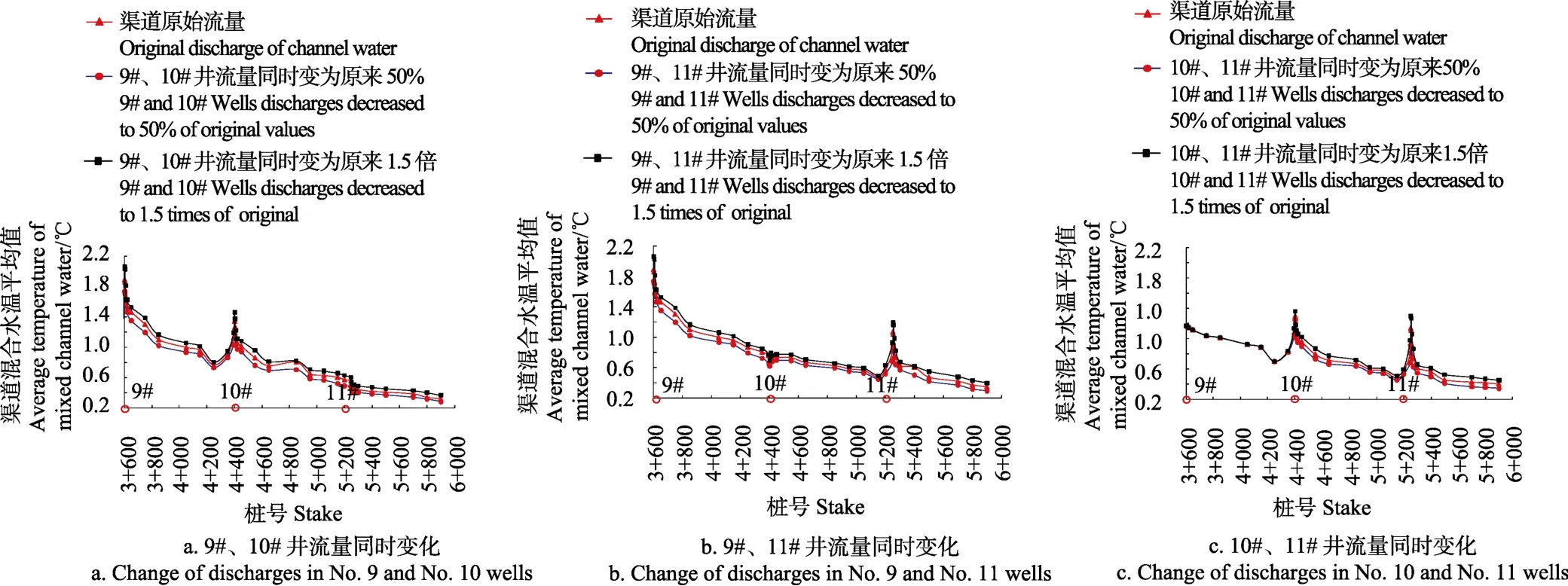
图7 双井井水流量对渠道混合水温的影响Fig.7 Effect of well discharges with two wells on temperature of mixed channel water
图 7分别给出了连续双井和间隔双井流量变化对渠道混合水温的影响变化过程,从图中可以看出,在加入井水后,渠道水温立即上升,充分混合后沿程逐渐降低,而且混合后水温下降较快,在融冰井下游250 m左右水温降低开始变缓,直至下一口融冰井水的加入;而且以上3种工况都可以明显看出在下一口融冰井前100 m左右,由于下游井水的加入,渠道水温有升温趋势,说明每一口融冰井不仅影响下游渠道水温,而且对上游一定距离的渠道水温也有一定影响。图7a中9#、10#井井水流量降低和升高为原来的50%和1.5倍后,渠道混合水温降低和上升的最大幅度分别为 13.64%和 13.09%;图 7b中9#、11#井井水流量降低和升高为原来的50%和1.5倍后,渠道混合水温降低和上升的最大幅度分别为17.10%和11.48%;图7c中10#、11#井井水流量降低和升高为原来的50%和1.5倍后,渠道混合水温降低和上升的最大幅度分别为14.30%和13.63%。由于井水的热量有限,只对一定距离的渠水有增温作用,所以图7b中,因10#井流量保持不变,相比图7a中9#、10#井流量同时变化时增温效果较弱,在桩号 5+900位置,其对渠道水温的增温效果降低了14.67%,且渠道混合水温降低和上升的最大幅度分别有所升高和降低,从而可知增大井水流量对渠道增温效果明显,这对实际工程有较强的指导作用。
2)多井井水流量变化对渠道混合水温的影响
其他边界条件不变,9#、10#、11#井水流量同时变为原来50%和1.5倍时,模拟抽水融冰效果,同样提取渠道水面沿程混合水温平均温度,获得渠道混合后水温的计算结果见图8。

图8 多井井水流量对渠道混合水温的影响Fig.8 Effect of well discharges with three wells on temperature of mixed channel water
从图 8中可以看出,在其他边界条件恒定工况下,渠水与井水充分混合后的水温与井水流量成正比,且井水注入量越大,渠水的增温效应越显著。而且9#、10#、11#井水流量同时变为原来的50%和1.5倍时,渠道混合水温的降低和增高的最大幅度分别为18.39%和18.19%,平均变化幅度分别为11.46%和10.64%,这说明井水注入量变化对渠道混合后水温影响较为明显,井水汇入量的增大对渠水的增温有显著效果。但实际工程中升高井水温度很难实现,而通过合理运行融冰井群来控制井水注入渠道的流量可有效地提高渠水温度,从而更能有效地防治引水渠道冰害。
3.3.2 井前渠道水温变化对渠道混合水温的影响
在各融冰井水流量、水温,井前渠道流量等条件保持不变的工况下,模拟井前渠道水温变化对融冰效果的影响,同样根据实际工程中可能发生的情况,将井前渠道水温变化条件分别设置为:降低和升高0.2 ℃和0.4 ℃,提取渠道水面沿程混合水温平均值见图9所示。
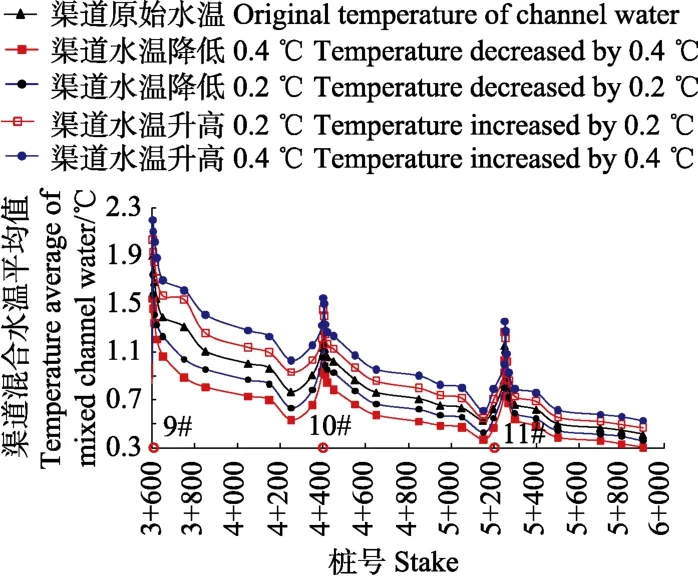
图9 不同井前渠道水温对渠道混合水温的影响Fig.9 Effect of temperature of channel water before well on mixed channel water temperature
从图 9计算结果看出,混合后的渠道水温与井前渠道水温成正比,井前渠道水温对融冰结果有较大的影响。从融冰增温效果上来看,在井前渠道水温下降 0.4 ℃和0.2 ℃的工况下,相对于原始井前渠道水温下的混合水温,渠道混合水温平均降幅分别为22.61%和11.41%;而在井前渠道水温上升0.2 ℃和0.4 ℃时,混合水温平均增幅分别为11.25%和22.57%。可知井前渠道水温下降0.4 ℃时渠道混合水温的降幅与井前渠道水温上升 0.4 ℃时渠道混合水温的增幅基本一致,井前渠道水温下降0.2 ℃时渠道混合水温的降幅也基本等于井前渠道水温上升 0.2 ℃时渠道混合水温的增幅。而且根据模拟结果还发现,井前渠道水温上升或下降0.10 ℃,渠道混合水温也上升或下降0.10 ℃左右,井前渠道水温变化对渠道混合水温影响较为明显。在气候寒冷时,实际工程运行中引水渠道水温随着气温沿程逐渐降低,很容易降低至冰点形成冰害,提高渠水温度来防止渠道冰害更为直接有效,此时可采取增加融冰井数量、减小融冰井间距等合理布局融冰井的方法来解决。
3.4 井群合理优化布置
由原型观测数据及模拟计算结果均可知,随着距融冰井注水口距离越远,沿程水温逐渐降低,但可以发现沿程水温均明显超过水的冰点。究其原因可能是上一口井井水加入后,使渠道水温度升高,而外界气温还不够低,混合水温沿程下降缓慢,没有降到足够低时又有新的井水加入,从而使得沿程水温超过冰点。原型观测中,由于在9#井注水点之前的渠道引水温度(T=1.37 ℃)较高,所以在此模型基础上,模拟计算了无井运行时沿程水温变化,计算结果得出下游桩号5+900处(12#井所在位置)渠道水温为0.25 ℃(>0 ℃),即表明在此大气温度条件下,并不需要外界井水热量的注入就可保证该渠段正常运行;而在桩号6+600处(13#井所在位置)运行一口融冰井即可保证后续渠段正常运行。
为探讨融冰井群的合理优化布置,现以此模型为基础,分别模拟不同井前渠道流量和大气温度工况下引水渠道的沿程水温变化,为寒区各水电站冬季安全稳定运行提供参考。
3.4.1 不同井前渠道流量条件下井群的合理布置
井水流量(9#、10#、11#融冰井水流量分别为0.18、0.13、0.16 m3/s)、井水温度(9#、10#、11#井水温度分别为 10、10、9.6 ℃)、大气温度(T气= –2、–1.5、–1.0 ℃)等条件保持不变,井前渠道水温设置为0.1 ℃,分别模拟井前渠道流量为10、15、20和25 m3/s时沿程混合水温变化,得到各井的不冻长度(不冻长度即渠水温度大于0 ℃的渠段长度)见表2。
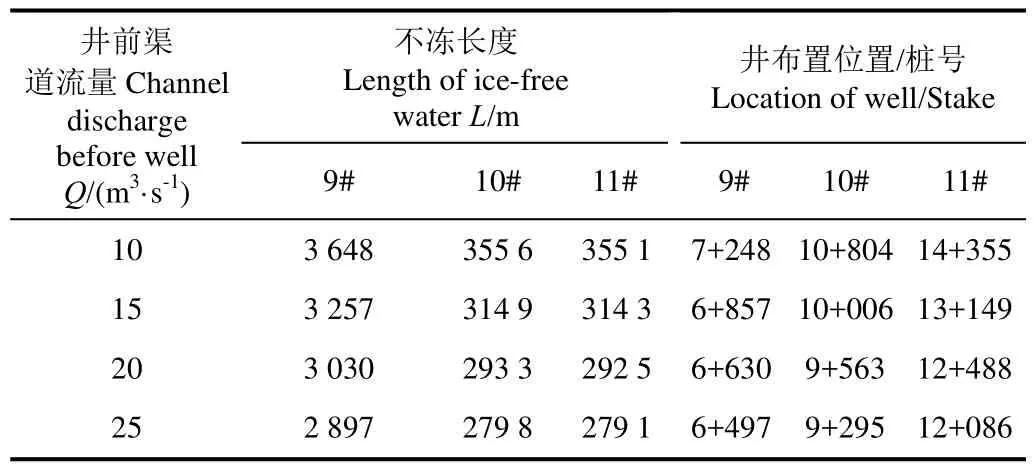
表2 不同井前渠道流量下各井的不冻长度和位置Table 2 Values and location of length of ice-free water for each wells at different channel discharges before well
从表 2可以明显看出,随着井前渠道流量的增大,融冰井的不冻长度随之减短,这是由于渠道引水水温远低于井水温度,当井前渠道流量变大,井水对渠水的增温效果被削弱。还可以发现因井前渠道流量增大,无疑会导致渠道流速增大,随之产生的动能在一定程度上部分转化为水的热能,所以随着井前渠道流量增大,融冰井的不冻长度逐渐减小。在不同井前渠道流量条件下,根据各融冰井不冻长度合理布置井群。
3.4.2 不同大气温度条件下井群的合理布置
同样将井前渠道水温设置为 0.1 ℃,井前渠道流量(Q=10.57 m3/s)、各井井水流量(9#、10#、11#融冰井井水流量分别为0.18、0.13、0.16 m3/s)、井水温度(9#、10#、11#井水温度分别为10、10、9.6 ℃)等条件不变,根据严寒地区冬季常见气温,分别模拟外界大气温度为–5、–10、–20和–30 ℃时沿程混合水温变化,得到各井的不冻长度模拟结果如表3。
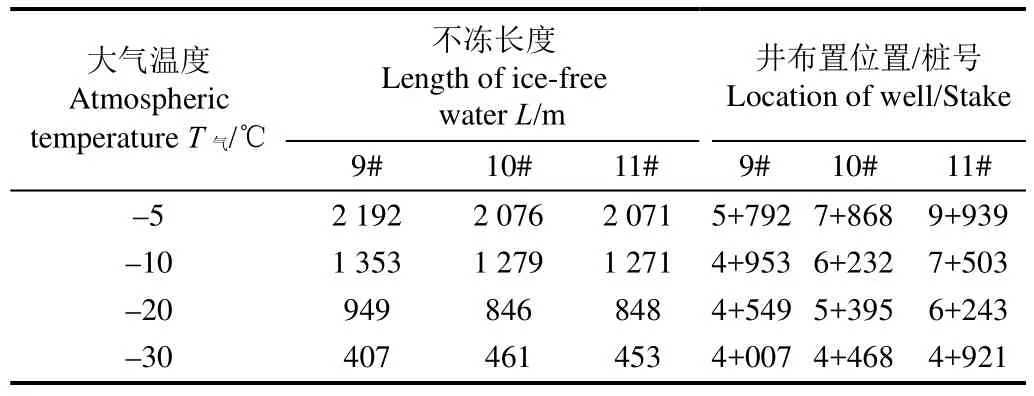
表3 不同大气温度下各井的不冻长度和位置Table 3 Values and location of length of ice-free water for each wells at different atmospheric temperatures
从表 3可以看出,在相同大气温度下,各融冰井的不冻长度并不一样,而这部分长度差是由于每口井的抽水流量和井水温度等不一样所致;还可以看出随着外界大气温度的降低,融冰井的不冻长度也随之减小,在低于零下10 ℃时,大气温度每降低10 ℃,融冰井不冻长度按每400 m左右递减。而在不同外界大气温度条件下,依据融冰井不冻长度便可合理布置井群。
4 结 论
根据红山嘴电站二级引水渠道,建立3D紊流数学模型,通过模拟计算不同工况下引水渠道抽水融冰过程,分析了抽水融冰过程,具体结论如下:
1)以原型实测数据为边界条件对二级电站引水渠沿程水温变化进行模拟计算,并将其计算结果与原型观测结果进行了对比,平均相对误差为4.61%,表明两者符合较好,证明了后续模拟结果的可靠性;
2)当井前渠道流量、水温等保持不变,各井井水流量变为原来50%和1.5倍工况计算结果可以得知,井水注入流量与混合水温成正比;而当渠道水温分别降低和升高0.2 ℃、0.4 ℃,其他条件不变工况下的模拟结果表明,井前渠道水温与混合水温成正比,且井水流量变化与井前渠道水温变化对混合水温的影响均较为明显;因此增大井水流量或者合理布置井群是抽水融冰最有效的方法;
3)随着较高温度井水的加入,每一口融冰井不仅影响下游渠道水温,而且对上游一定距离的渠道水温也有一定影响;
4)分别模拟了渠道水温为0.1 ℃时,在不同井前渠道流量(10、15、20、25 m3/s)和不同大气温度(–5、–10、–20、–30 ℃)下的沿程水温变化,得到了各井的不冻长度值,且随着井前渠道流量增大,融冰井的不冻长度逐渐减小;随着大气温度降低,融冰井的不冻长度也减小;根据模拟结果还分别提出了井群的合理优化布置方案。
[1] 陈明千. 西藏高寒地区引水渠道冰花生消规律研究[D].成都:四川大学,2006.Chen Mingqian. Study on the Process of Ice Formation and Melting in Diversion Channel of Tibet[D]. Chengdu: Sichuan University, 2006. (in Chinese with English abstract)
[2] 邓朝彬,刘柏年. 香加水电站引水渠冬季注水升温运行发电实践经验介绍[J]. 农田水利与小水电,1987(7):43-45.
[3] 王文学,丁楚建. 抽井水入发电渠道冬季运行试验及其计算[J]. 农田水利与小水电,1991(12):35-41.Wang Wenxue, Ding Chujian. Experiments and calculations for winter operation with pumping well water into power canal[J]. China Rural Water and Hydropower, 1991(12): 35-41.(in Chinese with English abstract)
[4] 刘新鹏,张治山,陈荣. 梯级引水式水电站群提高发电生产能力的途径[J]. 中国水能及电气化,2007(9):38-43.Liu Xinpeng, Zhang Zhishan, Chen Rong. Ways of improving the generation output by cascade-diversion type power station[J]. China Water Power and Electrification, 2007(9):38-43. (in Chinese with English abstract)
[5] 刘新鹏,陈荣,张治山. 红山嘴电厂抽水融冰技术新探索[J]. 中国水能及电气化,2008(4):29-36.
[6] 王峰,吴艳华,马月俊,等. 红山嘴梯级水电站抽水融冰技术应用与探讨[J]. 河南水利与南水北调,2009(7):111-112.
[7] 高霈生,靳国厚,吕斌秀. 南水北调中线工程输水冰情的初步分析[J]. 水利学报,2003,34(11):96-102.Gao Peisheng, Jin Guohou, Lü Binxiu. Preliminary study on ice regime in the middle route of south to north water transfer project[J]. Journal of Hydraulic Engineering, 2003, 34(11):96-102. (in Chinese with English abstract)
[8] 郭新蕾,杨开林,付辉,等. 南水北调中线工程冬季输水冰情的数值模拟[J]. 水利学报,2011,42(11):1268-1276.Guo Xinlei, Yang Kailin Fu Hui, et al. Numerical simulation of ice regime in the water conveyance system during winter in Middle Route of South-to-North Water Transter Project[J].Journal of Hydraulic Engineering, 2011, 42(11): 1268-1276.(in Chinese with English abstract)
[9] 吴剑疆,茅泽育,王爱民,等. 河道中水内冰演变的数值计算[J]. 清华大学学报:自然科学版,2003,43(5):702-705.Wu Jianjiang, Mao Zeyu, Wang Aimin, et al. Numerical simulation of frazil ice evolution in rivers[J]. Journal of Tsinghua University: Natural Science, 2003, 43(5): 702-705.(in Chinese with English abstract)
[10] 茅泽育,吴剑疆,张磊,等. 天然河道冰塞演变发展的数值模拟[J]. 水科学进展,2003,14(6),700-705.Mao Zeyu, Wu Jianjiang, Zhang Lei, et al. Numerical simulation of river ice jam[J]. Advances in Water Science,2003, 14(6), 700-705. (in Chinese with English abstract)
[11] 茅泽育,张磊,王永填,等. 采用适体坐标变换方法数值模拟天然河道河冰过程[J]. 冰川冻土,2003,25(2),214-219.Mao Zeyu, Zhang Lei, Wang Yongtian, et al. Numerical simulation of river-ice process using boundary-fitted coordinate[J]. Journal of Glaciology and Geocryology, 2003,25(2), 214-219. (in Chinese with English abstract)
[12] 茅泽育,许昕,王爱民,等. 基于适体坐标变换的二维河冰模型[J]. 水科学进展,2008,19(2),214-223.Mao Zeyu, Xu Xin, Wang Aimin, et al. Han2D numerical model for river-ice processes based upon body-fitted coordinate[J]. Advances in Water Science, 2008, 19(2), 214-223. (in Chinese with English abstract)
[13] 曾平,段杰辉,黄柱崇,等. 二维流冰消融数学模型[J]. 水利学报,1997(5):15-22.Zeng ping, Duan Jiehui, Huang Zhuchong, et al. Two dimensional numerical model of turbulent flow and ice melting[J]. Journal of Hydraulic Engineering, 1997(5): 15-22. (in Chinese with English abstract)
[14] 陈武,刘德仁,董元宏,等. 寒区封闭引水渡槽中水温变化预测分析[J]. 农业工程学报,2012,28(4):69-75.Chen Wu, Liu Deren, Dong Yuanhong, et al. Prediction analysis on water temperature in closed aqueduct in cold regions[J]. Transactions of the Chinese Society of Agricultural Engineering, 2012, 28(4): 69-75. (in Chinese with English abstract)
[15] 王晓玲,张自强,李涛,等. 引水流量对引水渠道中水内冰演变影响的数值模拟[J]. 水利学报,2009,40(11):1307-1312.Wang Xiaoling, Zhang Ziqiang, Li Tao, et al. Numerical simulation of diversion water flux effect on frazil ice evolution in diversion channel[J]. Journal of Hydraulic Engineering, 2009, 40(11): 1307-1312. (in Chinese with English abstract)
[16] 王晓玲,周正印,蒋志勇,等. 考虑气温变化影响的引水渠道水内冰演变数值模拟[J]. 天津大学学报:自然科学与工程技术版,2010,43(6):515-522.Wang Xiaoling, Zhou Zhengyin, Jiang Zhiyong, et al.Numerical simulation of frazil ice evolution in diversion channel considering effect of temperature variation[J].Journal of Tianjin University, 2010, 43(6): 515-522. (in Chinese with English abstract)
[17] 杜一民,译. 引水道式农村水电站的冰冻问题[M]. 北京:水利电力出版社,1959.
[18] Shen Hungtao, Sun Junshan, Liu Lianwu. SPH simulation of river ice dynamics[J]. Journal of Computational Physics,2000, 165(2): 752-770.
[19] Liu L, Li H, Shen H T. A Two-dimensional comprehensive river ice model[C]//. Proceedings of the 18th IAHR International Symposium on Ice. Sapporo, 2006: 69-76.
[20] Shen H T, Lu S. Dynamics of river ice jam release [C] //.Proceedings of Cold Regions Engineering: The Cold Regions Infrastructure—An International Imperative for the 21st Century, New York, 1996: 594-605.
[21] Jasekatal M, Muste M, Ettema R. Estimation of Yukon river discharge during an ice jam near Dawson city[J]. Canadian Journal of Civil Engineering, 2001, 28(5): 856-864.
[22] Wang S M, Doering J C, P E, et al. Numerical simulation of supercooling process and frazil ice evolution[J]. Journal of Hydraulic Engineering, 2005, 131(10): 889-897.
[23] Chen F, Shen HT, Andres D, et al. Numerical simulation of surface and suspended freeze-up ice discharges[C]//World Water and Environmental Resources Congress: Impacts of Global Climate Change. Florida: CRC Press, 2005: 1-10.
[24] Betchelor G K. Mass transfer from small particles suspended in turbulent fluid[J]. Journal of Fluid Mechanics, 1980, 98:609-623.
[25] Wadia P H. Mass transfer from sphere and discs in turbulent agitated vessels[D]. Massachusetts: Massachusetts Institute of Technology, 1974.
[26] 吴素杰,宗全利,郑铁刚,等. 高寒区引水渠道抽水融冰水温变化过程模拟[J]. 农业工程学报,2016,32(14):89-96.Wu Sujie, Zong Quanli, Zheng Tiegang, et al. Simulation on water temperature change process of diversion channel for pumping well water to melt ice at high altitude and cold regions[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(14): 89-96. (in Chinese with English abstract)
[27] 郑铁刚,孙双科,柳海涛,等. 大型分层型水库下泄水温对取水高程敏感性分析研究[J]. 水利学报,2015,46(6):714-722,731.Zheng Tiegang, Sun Shuangke, Liu Haitao, et al. Sensibility analysis of intake elevation on water temperature discharged from a large thermal stratified reservoir[J]. Journal of Hydraulic Engineering, 2015, 46(6): 714-722,731. (in Chinese with English abstract)
[28] 邓云. 大型深水库的水温预测[D]. 成都:四川大学,2013.Deng Yun. Study on the Water Temperature Prediction Model for the Huge and Deep Reservoir[D]. Chengdu:Sichuan University, 2013. (in Chinese with English abstract)
[29] 龙天渝,蔡增基. 流体力学[M]. 北京:中国建筑工业出版社,2004:90-115.
[30] Moriasi D N, Arnold J G, Liew M W V, et al. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations[J]. Transactions of the ASABE(American Society of Agricultural and Biological Engineers), 2007, 50(3): 885-900.
3D simulation on water temperature change of diversion channel and optimal arrangement of multi-wells at high altitude and cold regions
Wu Sujie1, Zong Quanli1※, Zheng Tiegang2, Wang Zijian3, Liu Zhenji1
(1.College of Water Conservancy and Architectural Eengineering, Shihezi University, Shihezi,832000,China;2.Sate Key Laboratory of Simulation and Regulation of Water Cycle in River Basin, China Institute of
Water Resources and Hydropower Research, Beijing100038,China;3.Surveying and Designing Institute(Group)Co., Ltd of Xinjiang Production and Construction Crops, Shihezi,832003,China)
In the northwest high altitude and cold regions, it’s easy to produce ice for the long distance of diversion channel of diversion power station. Pumping well water to melt ice is an effective method to solve the ice problem for diversion power station in winter. In order to investigate the effect of pumping well water to melt ice on the increase of channel water temperature, the second diversion channel of Hongshanzui Water Power Station in Manas River of Xinjiang was selected as the study area, and a three-dimensional turbulence numerical model was proposed to simulate the change process of water temperature of diversion channel under the condition of multi-well running at the same time. The change process of water temperature obtained from the simulation was compared with that from the prototype observation experiment, and the results indicated that the calculation results were in a good agreement with the prototype observation results. The average relative error between them was 4.61%, which verified the reliability of the numerical simulation. Thus, the water temperature change processes of diversion channel were simulated under the conditions of different discharge of well water, different discharge and temperature of channel water before wells, and different atmospheric temperature. Firstly, when the discharge and temperature of channel water were constant, and the discharge of well water was decreased by half or increased by half compared with the original value, the mixed water temperature was proportional to the discharge of well water and sensitive to it. At the same time, when the temperature of channel water was decreased and increased by 0.2 and 0.4 ℃, respectively, the mixed water temperature was proportional to the temperature of channel water and sensitive to it. It is concluded that it is the most effective way to pump well water to melt ice by increasing the discharge of well water and arranging the well group rationally. During the process of melting-ice wells running, each well not only affected the downstream water temperature, but also affected the upstream water temperature in some distance. According to the simulated results under the temperature of channel water of 0.1 ℃, the discharge of channel water of 10, 15, 20 and 25 m3/s, and the atmospheric temperature of -5, -10, -20 and -30 ℃,respectively, the different value of the ice-free water length of each well was calculated. The results showed that the length of the ice-free water for each well decreased with the increase of channel water discharge before wells and the decrease of atmospheric temperature. Based on the calculated length of the ice-free water for each well, the reasonably optimized results of the length of the ice-free water and the arrangement of the wells were proposed under different discharges of channel water before wells and different atmospheric temperatures. This study can provide valuable information for preventing ice hazards of diversion channel in the cold regions.
temperature; wells; optimization; diversion channel; pumping well water to melt ice; numerical simulation; length of ice-free water
10.11975/j.issn.1002-6819.2017.14.018
TK79
A
1002-6819(2017)-14-0130-08
吴素杰,宗全利,郑铁刚,王子坚,刘贞姬. 高寒区多口融冰井引水渠道水温变化三维模拟及井群优化布置[J]. 农业工程学报,2017,33(14):130-137.
10.11975/j.issn.1002-6819.2017.14.018 http://www.tcsae.org
Wu Sujie, Zong Quanli, Zheng Tiegang, Wang Zijian, Liu Zhenji. 3D simulation on water temperature change of diversion channel and optimal arrangement of multi-wells at high altitude and cold regions[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(14): 130-137. (in Chinese with English abstract)
doi:10.11975/j.issn.1002-6819.2017.14.018 http://www.tcsae.org
2016-11-17
2017-02-27
国家自然科学基金资助项目(51269028);2015年度留学人员科技活动择优资助项目。
吴素杰,女(土家族),重庆人,主要从事工程水力学方面研究。石河子 石河子大学水利建筑工程学院,832000。
Email:836619533@qq.com。
※通信作者:宗全利,男,山东临朐人,教授,博士,主要从事水力学及河流动力学方面研究。石河子 石河子大学水利建筑工程学院,832000。
Email:quanli1871@126.com。

