基于尤拉差分法的水库调洪演算最高水位的算法研究
杨 莉,李双江,周 斌
(1.三门峡市水利勘测设计有限责任公司,河南 三门峡 472000;2.汕尾市水利水电规划设计院,广东 汕尾 516600)
基于尤拉差分法的水库调洪演算最高水位的算法研究
杨 莉1,李双江1,周 斌2
(1.三门峡市水利勘测设计有限责任公司,河南 三门峡 472000;2.汕尾市水利水电规划设计院,广东 汕尾 516600)
为确定水库洪水位,需要根据水量平衡原理进行调洪演算。工程中通常采用固定时段计算水库入、出库水量和库水位的变化,但水库水位达到最高水位并不一定出现在固定时段的整点位置。固定时段影响了最高洪水位的计算精度。引入二分法、不动点迭代、拟Newton法等数值算法单独求解最高洪水位,可以大幅提高计算精度。
水量平衡;调洪演算;最高水位;算法
为确定水库洪水位,需要根据水量平衡原理进行调洪演算,工程中通常采用尤拉差分法[1]按固定时段逐时段计算水库入、出库水量和库水位的变化。但水库水位达到最高水位并不一定出现在固定时段的整点位置,从而使固定时段的最高洪水位成果偏低,因此最高洪水位的计算不宜采用固定时段,宜采用专门的算法。
1 调洪演算的尤拉解法
对于任一时段(如t1→t2),入库水量减去出库水量,应等于该时段内水库增加或减少的蓄水量,尤拉差分法的调洪演算计算公式为:
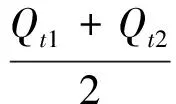
(1)
式中:Qt1、Qt2为时段始、末的入库流量;qz1、qz2为时段始、末的出库流量,取决于库水位z,即q=f(z);Vz1、Vz2为时段始、末的库容,取决于库水位z,即V=f(z);△t为计算时段,△t=t2-t1。
预先确定△t再计算时,式(1)即为变量为z2的一元非线性方程,可采用二分法、不动点迭代法、Newton迭代法及其它数值分析方法求解,也可采用半图解法等工程方法求解[2]。
2 最高洪水位的基本方程
设在时间t=t2水库水位过到最高洪水位,虽然有dz/dt=0,但对式(1)求导展开式过于复杂。注意到最高洪水位时有Qt2=qz2,引入该条件后式(1)可写为:

(2)
Q(t2)=q(z2)
(3)
式(2)和式(3)构成的方程组有未知数t2、z2,为二元非线性方程组,水库最高水位的求解即转化为对二元非线性方程组的求解。
3 最高洪水位的解法
非线性方程组的常规解法有不动点迭代法、Newton法或拟Newton法,式(2)和式(3)构成的方程组仅为二元函数,也可转化后采用非线性方程的二分法求解。
3.1 二分解法
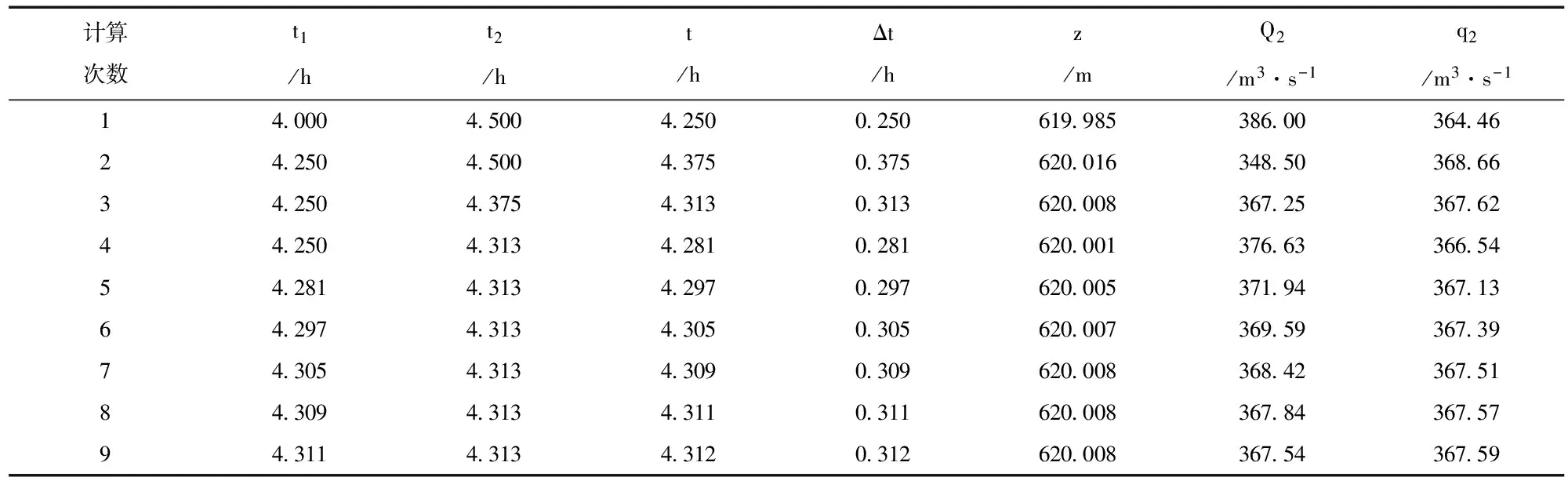
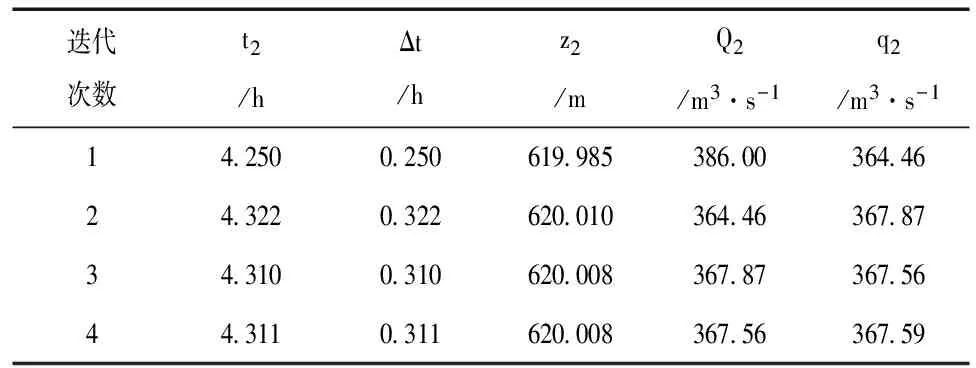
注意到库水位上升期有Q(t2)>q(z2)、库水位下降期有Q(t2) 1)准备:初步确定解区间[t1,t2],使Q(t1)>q(z1)、Q(t2)>q(z2)。 3)计算:令△t=t-t0,代入式(1)求解。 4)验证:t2-t1<ε(ε为事先指定的计算精度)或前后相邻两次计算的最高库水位z满足事先指定的精度,转步5;否则若Q(t)>q(z),令t1=t,转步2。若Q(t) 5)结束:取计算所得的z为最高库水位、t为最高库水位的发生时间。 3.2 不动点迭代解法 采用不动点迭代解法可按以下步骤求解: 自我修炼具有引导教育自己朝着理想目标前进的能力与功效,能够为自己前进指明方向,帮助自己坚定理想信念,强化宗旨意识。外部监督使自我修炼取得的成果通过外部监督固化下来,使自我修炼的基本原则与基本方法通过外部监督固化下来。在实际工作中,以领导干部掌握马克思主义理论这个看家本领为着力点,夯实自我修炼与外部监督同频共振的坚实基础;以发展积极健康的党内政治文化为着力点,为自我修炼与外部监督互促共进提供良好环境;以强化制度执行力为着力点,为自我修炼与外部监督和衷共济提供强力支撑。 2)迭代:将t2代入式(2)计算,得到z2;根据式(3)有t2=Q-1[q(z2)]。 3)验证:比较前后相邻两次计算的最高库水位z2和发生时间t2,如满足事先指定的精度则转步4,否则转步2。 4)结束:取计算所得的z为最高库水位、t为最高库水位的发生时间。 迭代法可进一步引入延拓法的思想,引入参数0≤λ≤1,将步2迭代初值和迭代终值的t2、z2进行加权,即取t2=λt2初+(1-λ)t2迭和z2=λz2初+(1-λ)z2迭,可大幅提高迭代算法的收敛性。 3.3 拟Newton法 (4) Qt1+mQ×(t2-t1)=qz1+mq×(z2-z1) (5) 式(4)和式(5)组成二元线性方程组,变形后为: (6) (7) 计算时可先预估z2、t2,求得Q(t2)、q(z2)、mv、mQ、mq等参数代入式(6)、式(7)再重新求解z2、t2,依次迭代直至满足解答精度要求。可参照以下步骤求解: 1)准备:预估初始解(t2,z2)。 2)准备:根据初始解答(t2,z2)计算参数Q(t2)、q(z2)、mv、mQ、mq。 3)计算:按式(6)、式(7)可得新的迭代解t2,z2。 4)验证:比较前后相邻两次计算的最高库水位z2和发生时间t2,如满足事先指定的精度则转步5,否则将迭代解或采用延拓法加权后的解作为初始解转步2。 5)结束:取迭代解t2,z2为最终解。 池芦水库位于黄河流域洛河水系支流永昌河上,坝址控制流域面积18.10km2,是一座以灌溉、供水为主,兼有防洪任务的小(1)型水库,防洪标准为30a一遇设计、300a一遇校核[3]。池芦水库溢洪道为无闸控制的岸边开敞式,控制段为顶宽30m、堰顶高程616.0m的宽顶堰。按0.5h固定时段计算的池芦水库校核洪水调洪过程见表1。 表1 池芦水库校核洪水调洪过程(0.5h固定时段) 显然,池芦水库遭遇校核洪水的最高水位将发生在时段4-4.5h,需进一步细化核准最高水位。 4.1 二分解法 取计算时段初始的入库流量461m3/s,出库流量319.63 m3/s,初始水位619.648m,解区间为[4,4.5]。迭代计算的过程见表2。 表2 池芦水库遭遇校核洪水最高水位的二分法计算过程 4.2 不动点迭代解法 取计算时段初始的入库流量461m3/s,出库流量319.63 m3/s,初始水位619.648m,取初始解t2=4.25h。池芦水库遭遇校核洪水最高水位迭代计算过程见表3。 表3 迭代法计算过程 4.3 拟Newton法 取计算时段初始的入库流量461m3/s,出库流量319.63 m3/s,初始水位619.648m,取初始解t2=4.25h、Z2=620.0m。拟Newton法的迭代过程见表4。 为确定水库洪水位,需要根据水量平衡原理进行调洪演算。工程中通常采用固定时段计算水库入、出库水量和库水位的变化,但水库水位达到最高水位并不一定出现在固定时段的整点位置,影响最高洪水位成果的精度,因此最高洪水位的计算不宜采用固定时段。最高洪水位的计算可采用二分法、不动点迭代、拟Newton法等数值,可以大幅提高计算精度取得较好的计算效果。 表4 池芦水库遭遇校核洪水最高水位的拟Newton法迭代过程 [1]叶守泽,许静仪,王祥三,等.水文水利计算[M].北京:中国水利水电出版社,1992:62-70. [2]郑咸义,姚仰新,雷仁秀,等.应用数值分析[M].广州:华南理工大学出版社,2008:45-51. [3]李双江,杨莉,周建波,等.陕县池芦抗旱小水库水源工程项目建议书[R].三门峡:三门峡市水利勘测设计有限责任公司,2015. HighestWaterLevelAlgorithmStudyonReservoirStorageRoutingBasedonEulerDifferenceMethod YANG Li1;LI Shuang-jiang1and ZHOU Bin2 (1.Sanmenxia Urban Water Conservancy Investigation and Design Limited Company, Sanmenxia 472000, China; 2.Shanwei Urban Water Conservancy & Hydropower Planning and Design Institute, Shanwei 516600, China) In order to determine the reservoir flood level, it is necessary to carry out flood control calculation according to the principle of water balance. During the process of project construction, the fixed time is usually adopted to calculate the change of reservoir inlet and outlet water and reservoir water level, but the reservoir water level reaches the highest water level and not sure to appear in the fixed point of time. The fixed period affects the calculation accuracy of the highest flood level. It can greatly improve the calculation accuracy by introducing the dichotomy, fixed point iteration,quasi-Newton method and other numerical algorithm to solve the maximum flood level. water balance;storage routing;maximum water level; algorithm 1007-7596(2017)10-0017-03 TV697.13 B 2017-09-18 杨莉(1980-),女,河南三门峡人,工程师,从事水利水电工程规划工作;李双江(1985-),男,河南三门峡人,工程师,从事水利水电工程设计工作;周斌(1972-),男,广东汕尾人,高级工程师, 从事水利水电工程设计工作。



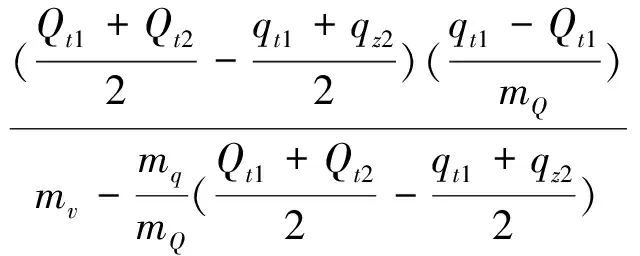

4 工程算例

5 结 语