基于双向拍卖的运输服务市场报价策略研究
杨玲


摘 要:文章将双向拍卖理论中的一些经典模型运用到运输服务市場中,对运输服务市场中的报价策略及其影响进行研究。在单线运输环境中,假设交易者不具有学习能力,通过构建托运人和承运商到达率相等,在报价空间内随机报价的仿真实验框架,对比各策略交易双方的累积收益、平均收益及累积成交量。研究发现采用ZIU报价策略的参与者收益较小,且其成交量更随机。实验将为参与者的报价策略及第三方拍卖商进行拍卖设计提供决策依据。
关键词:物流;双向拍卖;报价策略;K-ZI
中图分类号:U294 文献标识码:A
Abstract: In this paper, we studied the bidding strategy and the impact of the transport services market by the way of double auction. On the condition of single line transportation, ZIU, ZIC and K-ZI bidding strategies were contrasted, computer simulation experiment was implemented, then the trading volume and the income of shippers market were analyzed and contrasted respectively. It is found that the income of participants is smaller in ZIU strategy quotation, and the trading volume is stronger randomness in all strategies. The analysis of the conclusion will provide decision-making basis of auction design for participants in the transportation services market.
Key words: logistics; double auction; bidding strategy; K-ZI
0 引 言
近年来,运输服务市场的在线交易开始快速兴起,运输平台模式的出现将运输服务的供需方直接对接起来,为运输服务市场的交易双方带来了极大的便利。在以往运输服务的交易中,托运人往往首先提出所有线路的运输需求,承运商再分别对不同线路进行竞拍。在电子交易环境下,一些第三方服务通过在线平台实现,此类拍卖实质上是一种单物品逆向拍卖,最终会导致每条线路被分配到报价最低的承运商。除了托运人的运输作为拍卖对象外,承运商的运输能力也可以作为拍卖对象,这类以卖方为主导的拍卖被称为正向拍卖。现在基于拍卖的运输服务采购方面的研究大多集中于买方主导的逆向拍卖,这对交易者的计算能力提出了很高的要求。而双向拍卖机制[1]可以有效减轻交易者的计算负担,这一推断已在不同交易环境下被学者们所证实。
双向拍卖自Friedman教授在1956[2]年提出以来,已经广泛应用于证券交易、货币交易和其他商品交易市场,但在运输服务市场中,有关双向拍卖的理论研究却非常有限。考虑到运输服务市场中拥有诸多托运人和承运商,双向拍卖可以有效地提高交易效率和优化市场的资源配置,在线交易平台为双向拍卖的实施创造了非常便利的条件,国外一些大型物流综合网站(比如www.leanlogistics.com,www.besttransport.com,www.goubuy.com)已开始着手提供双向拍卖服务,同样的,有些公司也开始购买一些第三方物流公司的运输服务,比如沃尔玛虽然拥有自己的私人车队,但在其需求量过大的时候仍会通过物流电子市场购买运输服务[3]。尽管业界已经开始将拍卖理论运用到运输服务市场,但目前学术界关于双向拍卖的研究却非常有限。在这些研究中,张璐和丁静之[4]基于公路货运联盟和公路货运平台模式研究了组合拍卖机制下的公路货运平台的订单分配问题。李梦和黄海[5]军从有限理性人的观点出发提出了一种兼顾运量分配与均衡配流的组合模型。Huang和xu[6-8]首先关注于在线公路运输市场中双向拍卖机制的设计,为运输服务市场的在线拍卖模型提出了基本的理论框架。付秋芳[9]等人在基准点模型和拍卖双方报价策略的线性假设基础上,以追求运输市场整体效用最大化为目标,运用组合双向拍卖理论研究了我国公路运输市场在运输代理模式下的运输服务定价策略问题。Xu和Meng Cheng[10]等人以运输服务中的交易成本为出发点,基于拍卖理论研究了B2B电子物流市场的多式联运问题。在以上这些研究中,学者们大多将托运人和承运商对路线的保留价格进行竞拍(真实估价),并未考虑到在实际运输服务中,大多数交易者的最初定价只是一个参考价格,参与者往往会在综合考虑了市场中诸多因素后给出一个并不一定等于初始价格的进入市场报价。而所选的报价策略的选择将会直接影响参与者的最终收益。
本文将首先搭建一个在线的第三方物流交易平台,在此交易平台中以双向拍卖为交易实现方式设置基本的交易规则,对运输服务市场中的报价策略及影响进行研究。即在单线运输环境下,假设托运人与承运商到达率相同,研究约束型零信息ZIC,无约束型零信息ZIU和通用型零信息K-ZI报价策略,在MATLAB软件中进行计算机模拟实验,并对这三种策略的收益和成交量进行分析比较,做出相应推测,为进入市场的参与者进行拍卖设计提供决策依据。
1 基本模型
1.1 交易平台的搭建
在在线交易的运输服务市场中,第三方运输平台中的买方为有货运需求的托运人产生大量订单,而卖方为可以提供运输服务的运输企业及车队。这些在线订单我们称之为交易订单,而承运商可以通过构建的交易平台来获取订单信息并且完成相应的订单量,平台单件图如图1所示:endprint
2 实验过程
2.1 交易规则设定
考虑到运输服务市场的特殊性,即在满足双方价格最优匹配的约束条件下还要尽可能的使双方运量交易达到最大,本实验设置了一种3+n阶段的实验框架,来模拟运输市场的交易过程。实验框架设置如下:
第一阶段,按价格进行匹配。首先考虑交易者双方的报价,令报价最高的托运方与报价最低的承运方进行匹配,报价第二高的托运方与报价第二高的承运方进行匹配,以此类推,直到剩余所有托运方的报价都高于承运商方的报价此轮交易停止。此轮每对的成交价格定为相匹配的托运人报价与承运商报价的平均价格,成交量定为相配对的托运人运量与承运商运量中较小的运量值。
第二阶段,按运量进行匹配。上一轮匹配中完成运量匹配的交易者将离开市场,而完成部分匹配的交易者将已匹配部分从市场中剔除,将剩余市场中托运人与承运商方的剩余运量按从大到小的顺序排列。此轮匹配中,在满足约束条件为托运方单位报价大于承运方单位报价的条件下,令运量需求最多的托运方与可运载量最多的承运商进行匹配,运量需求第二多的托运方与可运载量第二多的承运商进行匹配,以此类推,直到满足以上约束条件的托运方与承运方均达成匹配则停止交易。此轮每对的成交价格定为相匹配的托运人报价与承运商报价的平均价格,成交量为相匹配的托运人运量与承运商运量中较小的运量值。
第三阶段,按估价及成本进行匹配。剔除上两步已经匹配的运输量,将单位运量初始估价最高的托运方与单位将托运人按初始的单位估价降序排列,承运商的单位运费成本按升序排列,按此排位将托运方与承运商匹配,此轮匹配的约束条件为每对交易价格小于所匹配的托运方单位估价且大于此对所匹配的承运商单位货运成本。同样,成交价格定为相匹配的托运人报价与承运商报价均值,成交量定为相配对的托运人运量与承运商运量中较小的运量值,且将已经参与匹配的参与者数量进行剔除,然后重复上述匹配直到市场中所有托运人方的估价高于承运商方成本的交易者均达成匹配,实验终止。实验框架简图如图2所示:
根据以上的报价策略及实验框架,本文针对运输服务市场设计了一个具体的仿真实验,并在MATLAB R2012b软件中實现了这一模拟。我们随机选取了模拟市场中的12个买方12个卖方,这些交易者的货运需求(可提供的货运力)和初始保留价格为设定区间内系统随机分配的,而报价分别是各自的保留价格通过采取ZIU、ZIC及K-ZI三种不同的报价策略随机报出,因而产生36组买方报价组和36组卖方报价组。初始设定中剔除了无效报价并默认所有参与者同意交易平台中关于货运量分配及成交价格方面的规则。
3 实验结果
本文将此实验随机重复进行了100次,每次实验中参与者的初始数据即货运需求(或可提供的运力)及保留价格都由计算机随机生成,计算了实验的总收益和每种策略的平均收益及成交量。由于市场中采用每种策略的参与双方人数相同而其运量为计算机随机生成,在此本文仅分析买方市场的交易情况。
3.1 总收益
总收益的计算公式为:
总收益=∑估价-交易价格*交易量
图3和表1分别为托运方中每种报价策略下的总收益及每种总收益的平均成交价。从图3及表1可看出参与者采用ZIU策略报价的总收益远小于采用ZIC、K-ZI策略的总收益。造成这种结果的原因也许是ZIU策略模拟的是市场中的无理性个体,采取此种策略的参与者在报价时不会考虑其预计收益;而K-ZI策略中的参数K代表着参与者的贪婪度,当K值越接近于1,参与者的报价越接近保留价格(真实估价)相当于参与者为了达成更高的成交量而造成每次成交时的收益较低。从图3中我们可以看到ZIU策略曲线的摆幅波动明显大于其他两种策略,甚至存在低于0的情况。虽然从收益的角度来看ZIU报价明显劣于其他两种策略,但在实际市场中,参与者可能通过此种报价吸引潜在的市场资源。
3.2 平均收益
平均收益的计算公式为:
平均收益=总收益/∑交易量
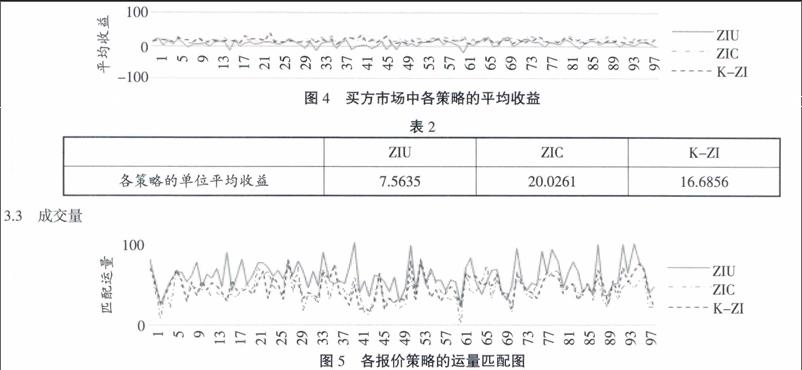
从图4及表2可看出参与者采用ZIU策略的平均收益远小于采用ZIC、K-ZI策略,而K-ZI报价策略又略低于ZIC报价策略。各策略的平均收益情况与总收益情况相似,从单笔成交收益来看仍然是ZIU劣于其他两种收益。
3.3 成交量
从图5 中发现每种报价策略下的匹配运量都具有较大的随机性,笔者认为,尽管在此次模拟实验中令参与实验的双方人数相等,但由于各自的运量(即托运人的货运需求量和承运商的可运量)随机生成,因此供需曲线也是系统随机分配,恰与实际市场中复杂的供需环境相似。
4 总 结
本文将双向拍卖理论运用于运输服务市场中,在此市场背景下研究了双向拍卖理论中的报价策略。基于运输服务市场的特性,即综合考虑市场中货运量和市场报价,构建了一个第三方交易平台的基本框架,此平台中的交易规则操作简单容易使用。在此交易规则下利用MATLAB软件模拟了运输服务市场中托运人和承运商的报价及运量匹配情况。具体而言,在单线路运输环境下,假设托运人与承运商到达率相同,对比了参与者采用各种报价策略的总收益、平均收益及双方交易量,研究发现采用无约束型零信息报价策略的参与者总收益及平均收益明显低于约束型零信息和通用型零信息报价策略,而市场中采用这几种报价策略的参与者的成交情况较为随机。本次模拟实验可为进入运输服务市场中的托运人和承运商提供报价方面的决策依据,也可为各类货运联盟及货运平台提供交易机制方面的参考。由于真实环境下运输服务市场的复杂性,我们必须充分考虑市场的供需变化及各种随机情况,将双向拍卖理论更好地运用到运输服务市场中,最大化提高社会资源利用率。因此,在今后的研究中,笔者将更具体地考察运输服务市场中托运人和承运商的报价行为和市场资源的分配情况,以此来研究参与者的报价策略及设置更贴近真实市场的匹配规则。endprint
參考文献:
[1] Freidman D, Rust J. The Double Auction Market: Institutions, Theories, and Evidence[M]. NEW York; Addison-Wesley, 1993.
[2] Friedman L. A Competitive Bidding Strategy[J]. Operations Research, 1956,4(1):104-112.
[3] Caplice C. Electronic markets for truckload transportation[J]. Production and Operations Management, 2007,16(4):423-436.
[4] 张璐. 公路货运平台订单分配问题研究[D]. 北京:北京交通大学(硕士学位论文),2016.
[5] 李梦,黄海军. 后悔视角下的运量分布与均衡配流组合模型[J]. 交通运输系统工程与信息,2016(3):15-20.
[6] George Q Huang, Su Xiu Xu. Truthful multi-unit transportation procurement auctions for logistics e-marketplaces[J]. Transportation Research Part B Methodological, 2013,47(1):127-148.
[7] Xu S X, Huang George Q. Transportation service procurement in periodic sealed double auctions with stochastic demand and supply[J]. Transportation Research Part B, 2013,56(1):136-160.
[8] Su Xiu Xu, George Q. Huang. Efficient auction for distributed transportation[J]. Transportation Research Part, 2014,65:47-64.
[9] 付秋芳,吴景豪,马士华,等. 基于运输代理商的公路运输服务拍卖定价模型[J]. 工业工程与管理,2013,18(5):41-47.
[10] Su Xiu Xu, Meng Cheng, George Q. Huang. Efficient intermodal transportation auctions for B2B e-commerce logistics with transaction costs[J]. Transportation Research Part B, 2015,80:322-337.
[11] Gode D K, Sunder S. Allocative efficiency of markets with zero intelligence (ZI) traders: market as a partial substitute for individual rationality[J]. Journal of Political Economy, 1993,101(1):119-137.
[12] Zhan W J, Zhang J L, Yang J, et al. K-ZI: A general zero-intelligence model in continuous double auction[J]. International Journal of Information Technology and Decision Making, 2002(1):673-691.endprint

