Uq(sl2)的若个子余代数的自同构群①

李雯樱 王 璐 陈惠香

(扬州大学 数学科学学院，江苏 扬州 225002)

Uq(sl2)的若个子余代数的自同构群①

李雯樱 王 璐 陈惠香

(扬州大学 数学科学学院，江苏 扬州 225002)

研究了三维单李代数的量子包络代数Uq的若干子余代数的自同构.首先构造了一个余代数C，证明C同构于Uq的某些子余代数，然后研究C的余代数自同构，给出所有这些自同构的表达式，由此刻画了C的余代数自同构群的结构.

量子包络代数，Hopf代数，余代数，余代数自同构，自同构群

0 引言

在代数学中，各种代数结构以及它们的自同构群是相当重要的研究内容，这是因为自同构群是代数结构的重要不变量，对代数结构的分类起着重要的作用．许多数学工作者都在从事这方面的工作．Kirkman, Procesi和Small给出了量子多项式代数kq[x,x-1,y,y-1]的自同构群[9].Artamonov 确定了量子多项式代数kq[x,x-1,y]的代数自同构形式[10].kq[x,x-1,y]实际上同构于量子群Uq的非负部分的Hopf代数，而有关量子群Uq的研究工作非常丰富[11, 12]. 利用逆向极限，Chen在文献[13]中描述了kq[x,x-1,y]的余代数自同构群的结构．本文在上述研究工作的基础上讨论uq的若干子余代数的自同构，我们将通过构造一个余代数C，证明C同构于Uq的某些子余代数，然后研究C的余代数自同构，给出所有这些自同构的表达式，由此刻画了C的余代数自同构群的结构.

1 预备知识

本文中恒设k是特征为零的代数闭域，我们在域k上展开讨论. 除非特别指出，本文中所出现的代数、余代数、Hopf代数等都定义在域k上. 用Z表示全体整数，N表示全体非负整数，k*表示k中非零元全体组成的乘法群.有关代数、余代数、Hopf代数等的基本概念和基本结论可参阅参考文献[8, 14, 15].

设0≠q∈k且q≠±1，三维单Lie代数sl2的量子包络代数Uq是一个结合k-代数，由四个元素E,F,K,K-1生成，关系式为：

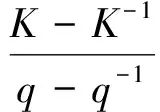
Uq是一个Hopf代数，其余代数结构和对极S由下述等式给出：

Δ(E)=1⊗E+E⊗K,S(E)=-EK-1,ε(E)=0,
Δ(F)=F⊗1+K-1⊗F,S(F)=-KF,ε(F)=0,
Δ(K)=K⊗K,S(K)=K-1,ε(K)=1,
Δ(K-1)=K-1⊗K-1,S(K-1)=K,ε(K-1)=1.

下面我们考虑Uq的若干子余代数.先构造一个余代数C,并讨论C的一些基本性质. 设C是一个k-线性空间，有基{gn,hn|n∈Z},定义k-线性映射Δ∶C→C⊗C和ε∶C→k为Δ(gn)=gn⊗gn，Δ(hn)=gn⊗hn+hn⊗gn+1，ε(gn)=1,ε(hn)=0，其中n∈Z,则有下述引理.

引理1 (C,Δ,ε)是一个余代数.

证明对任意的n∈Z，有(Δ⊗id)Δ(gn)=Δ(gn)⊗gn=gn⊗gn⊗gn=gn⊗Δ(gn)=(id⊗Δ)Δ(gn)和(Δ⊗id)Δ(hn)=Δ(gn)⊗hn+Δ(hn)⊗gn+1=gn⊗gn⊗hn+gn⊗hn⊗gn+1+hn⊗gn+1⊗gn+1=gn⊗Δ(hn)+hn⊗Δ(gn+1)=(id⊗Δ)Δ(hn),因此有(Δ⊗id)Δ=(id⊗Δ)Δ，进一步地有，(ε⊗id)Δ(gn)=ε(gn)gn=gn=(id⊗ε)Δ(gn),(ε⊗id)Δ(hn)=ε(gn)hn+ε(hn)gn+1=hn,和(id⊗ε)Δ(hn)=gnε(hn)+hnε(gn+1)=hn，因此，有(ε⊗id)Δ=(id⊗ε)Δ=id，故C是一个余代数．证毕．

引理2 设G(C)为余代数C的group-like元素之集，则G(C)={gn|n∈Z}.

证明直接验证可得．证毕．

2 余代数C的自同构群

在本节中，我们讨论C的余代数自同构.

引理3 设φ∶C→C是一个余代数自同构. 则存在一个整数r使得对任意的整数n有φ(gn)=gn+r和φ(hn)=αhn+r+β(gn+r-gn+r+1)，其中α,β∈k且α≠0.

证明由引理2知G(C)={gn|n∈Z}，将φ限制在G(C)上，得到G(C)到自身的一个双射，因此存在整数集Z的一个置换τ，使得φ(gt)=gτ(t)，t∈Z.

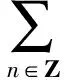
另一方面，有

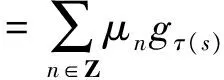
因此有

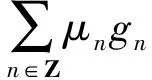
(1)

当n≠τ(s)且n≠τ(s+1)时，比较(1)式中项gn⊗gn的系数，得到μn=0；当n≠τ(s)时，比较(1)式中项gn⊗hn的系数，得到λn=0.因此(1)式就变为

λτ(s)hτ(s)⊗gτ(s)+1=(μτ(s+1)+μτ(s))(gτ(s)⊗gτ(s+1))+λτ(s)hτ(s)⊗gτ(s+1).

(2)

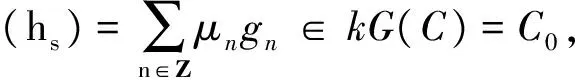
引理4 对于任意给定的整数r，定义线性映射σr∶C→C,σr(gn)=gn+r，σr(hn)=hn+r，n∈Z,则σr是C的一个余代数自同构.

证明显然σr是线性空间的自同构.又有(εσr)(gn)=ε(gn+r)=1=ε(gn)，(εσr)(hn)=ε(hn+r)=0=ε(hn)，因此有εσr=ε.进一步地，我们有(σr⊗σr)Δ(gn)=(σr⊗σr)(gn⊗gn)=σr(gn)⊗σr(gn)=gn+r⊗gn+r=gn+r⊗gn+r=Δ)gn+r)=Δσr(gn)和(σr⊗σr)Δ(hn)=(σr⊗σr)(gn⊗hh+hn⊗gn+1)=σr(gn)⊗σr(hn)+σr(hn)⊗σr(gn+1)=gn+r⊗hn+r+hn+r⊗gn+r+1=Δ(hn+r)=Δσr(hn),因此有(σr⊗σr)Δ=Δσr，故σr是C的一个余代数自同构．证毕．

我们用Aut(C)表示C的余代数自同构群，即Aut(C)是由C的全体余代数自同构关于映射合成作成的乘法群.令Γ={σr|r∈Z},则直接验证可知，Γ是Aut(C)的一个子群，且σrσt=σr+t，r，t∈Z. 因此，我们有下述引理.

证明显然σ是一个映射，并且是一个双射．对于任意的s,t∈Z，有σ(s+t)=σs+t=σsσt，因此σ是一个群同构映射．证毕．

令Aut0(C)={φ∈Aut0(C)|φ(g0)=g0).则直接验证可知Aut0(C)是Aut(C)的一个子群.由前面的引理3知，当φ∈Aut0(C)时，对任意的n∈Z有φ(gn)=gn.

引理6Aut0(C)是Aut(C)的一个正规子群，且Aut(C)同构于正规子群Aut0(C)与子群Γ的半直积.

证明任取φ∈Aut(C)，及φ′∈Aut0(C)，则由引理3知，存在一个整数，使得对任意的n∈Z，有φ(gn)=gn+r，因此对任意的n∈Z，有φ-1(gn)=gn-r，所以我们有(φφ′φ-1)(g0)=(φφ′)(g-r=φ(g-r)=g0，从而φφ′φ-1∈Aut0(C),因此Aut0(C)是Aut(C)的正规子群．又因为(φσ-r)g0)=φ(g-r)=g0，所以φσ-r∈Aut0(C)，于是φ=(φσ-r)σr∈Aut0(C)Γ，故Aut(C)=Aut0(C)Γ=ΓAut0(C)．显然Aut0(C)∩Γ={id}，这里id表示C上的恒等映射，也就是群Aut(C)的单位元．这样就证得了Aut(C)同构于正规子群Aut0(C)与子群Γ的半直积．证毕．

定理1 对于任意一簇非零纯量αn∈k*，n∈Z,及一簇纯量βn∈k，n∈Z,定义C的线性自同态φ∶C→为φ(gn)=gn，φ(hn)=αnhn+βn(gn-gn+1)，n∈Z.则φ是C的一个余代数自同构，且φ∈Aut0(C). 反之，任一个余代数自同构φ∈Aut0(C)具有上述形式.

证明设φ是定理中由给定纯量所定义的C的线性自同态，则φ显然是C的线性自同构. 下面验证φ是余代数同态，事实上，有(εφ)(gn)=ε(gn)和

(εφ)(hn)=ε[αnhn+βn(gn-gn+1)]=αn(ε(hn)+βnε(gn)-βnε(gn+1)=0=ε(hn)，

因此εφ=ε.进一步地，我们有

(φ⊗φ)Δ(gn)=(φ⊗φ)(gn⊗gn)=φ(gn)⊗φ(gn)=gn⊗gn=Δ(gn)=Δφ(gn)

和

(φ⊗φ)Δ(hn)=(φ⊗φ)(gn⊗hn+hn⊗gn+1)
=gn⊗(αnhn+βn(gn-gn+1))+(αnhn+βn(gn-gn+1))⊗gn+1
=αngn⊗hn+αnhn⊗gn+1+βngn⊗gn-βngn+1⊗gn+1
=αnΔ(hn)+βn(Δ(gn)-Δ(gn+1))
=Δ(αnhn+βn(gn-gn+1))=(Δφφ)(hn),

所以(φ⊗φ)Δ=Δφ，因此φ是C的余代数自同构，而且φ∈Aut0(C). 定理的最后一个论断由引理3得到．证毕．

φa(gn)=gn,φa(hn)=αnhn+βn(gn-gn+1),n∈Z,

(3)

而且φa∈Aut0(C).此时我们有如下结论.

=φaa′(hn),因此φ是一个群同态，从而是一个群同构．证毕．

其中σr和φa分别由引理5和命题1给出.

((σrφa)(σr′φa′))(gn)=gn+r+r′=(σr+r′φa·r′)a′)(gn)

和

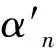
因此，(σrφa)(σr′φa′)=σr+r′φ(a·r′)a′，故定理中给出的映射是群同态，从而为群同构．证毕.

[1] Kulish P P, Reshetikhin N Yu. Quantum linear problem for the sine-Gordon equation and higher representations [J]. Zap Nauchn Sem Leninggrad Otdel Mat Inst Steklov (LOMI), 1981, 101: 101-110.

[2] Sklyanin E K. On an algebra generated by quadratic relations [J]. Uspekhi Mat Nauk, 1985, 40:214.

[3] Drinfeld V G. Hopf algebras and the quantum Yang-Baxter equation [J]. Dokl Akad Nauk SSSR,1985, 283: 1 060-1 064.

[4] Drinfeld V G. Quantum groups [C]. //Proc Int Cong Math (Berkeley, 1986). Amer Math Soc, Providence, RI, 1987.

[5] Jimbo M. A q-difference analogue ofU(g) and the Yang-Baxter equation [J]. Lett Math Phys, 1985, 10: 63-69.

[6] Alev J, Chamarie M. Derivations et automorphismes de quelques algebras quantique [J].Comm Algebra, 1992, 20: 1 787-1 802.

[7] Zha J G. Algebra automorphisms of quantized enveloping algebrasUq(g)[J]. Sci China Ser A, 1994, 37: 1 025-1 031.

[8] Kassel C. Quantum Groups [M]. New York: Springer-Verlag, 1995.

[9] Kirkman E, Procesi C, Small L. A-analog for the Virasoro algebra [J]. Comm Algebra, 1994, 22: 3 755-3 774.

[10] Artamonov V A. Actions of pointed Hopf algebras on quantum Torus [J]. Ann Univ Ferra-Ra- Sez,2005, 51: 29-60.

[11] Hu J, Zhang Y H. Quantum double ofUq(gl2)≤0[J]. J Algebra, 2007, 317: 87-117.

[12] Brown K A, Goodearl K R. Prime spectra of quantum semisimple group [J]. Trans Amer Math Soc, 1996, 349: 2 465-2 501.

[13] Chen H X. The coalgebra automorphism group of Hopf algebrakq[x,x-1,y][J]. J Pure Appl Algebra, 2013, 217: 1 870-1 887.

[14] Sweedler M E. Hopf Algebras [M]. New York: Benjamin, 1969.

[15] Montgomery S. Hopf Algebras and Their Actions on Rings [M]. CBMS Regional Conf Ser Math, Amer Math Soc, Providence RI, 1993.

AutomorphismGroupsofSeveralSubcoalgebrasofUq(sl2)

LI Wen-ying WANG Lu CHEN Hui-xiang

(School of Mathematical Sciences, Yangzhou University, Yangzhou 225002, China)

In this paper, we study the automorphisms of several subcoalgebras of the quantum enveloping algebraUqof three dimensional simple Lie algebra. We first construct a coalgebraC, and show thatCis isomorphic to some subcoalgebras ofUq. Then we study the automorphisms ofC. The coalgebra automorphisms ofCare all described, and the structure of the automorphism group of the coalgebraCare given.

quantum enveloping algebra, Hopf algebra, coalgebra, coalgebra automorphism, automorphism group

2017-05-10

国家自然科学基金项目(11571298)资助

陈惠香，E-mail：hxchen@yzu.edu.cn.

O153.3

A

1672-6634(2017)03-0017-04