正丙醇黏度方程研究
孟现阳,于野,吴江涛
(西安交通大学能源与动力工程学院,热流科学与工程教育部重点实验室,陕西 西安 710049)
正丙醇黏度方程研究
孟现阳,于野,吴江涛
(西安交通大学能源与动力工程学院,热流科学与工程教育部重点实验室,陕西 西安 710049)
正丙醇被广泛应用于化工、医药和农业等领域,可靠的热物性数据是理论研究和工程应用的基础。黏度作为流体重要的热物理性质之一,在生产流程的设计与优化和产品质量监测等方面具有重要意义。通过实验测量得到的黏度数据一般离散分布于不同的热力学状态,在工程中难以直接应用,因此,建立可靠的黏度方程以实现任意状态黏度的计算非常必要。经文献调研发现,目前缺少宽范围、高精度的正丙醇黏度方程,基于国内外已发表的实验数据开发了正丙醇高精度黏度方程。该方程不仅能够很好地复现实验数据,而且具有合理的外推性,其温度适用范围为150~400 K,压力适用范围为0.1~120 MPa,方程在计算范围内估计不确定度为1%~5%。
正丙醇;黏度;模型;热力学
引 言
正丙醇被广泛应用于化工、医药和农业等领域。在化工生产中,可以作为原料参与乙酸丙酯的生产;在医药生产中,可以用其制取黏合止血剂、红霉素等;在农业中,其衍生物可以用于制取菌达灭和灭草蜢等,此外其衍生出的醇醚类物质可以作为添加剂加入饲料中。正丙醇在不同领域的应用离不开准确的热物性数据,黏度作为其中一种重要的热物性参数,对于生产流程的设计与优化和产品质量监测等具有重要意义,因此对黏度进行研究有利于正丙醇在工程中的实际应用。虽然每年都有大量的黏度实验数据发表,但是这些数据一般离散分布于不同的温度和压力下,在工业应用中难以直接应用,因此有必要建立可靠的黏度方程以实现数据的连续计算。本文基于文献中公开发表的黏度实验数据,采用多参数黏度模型,开发了高精度、宽范围的正丙醇黏度方程。
1 黏度实验数据
通过系统全面的文献调研,对正丙醇黏度实验数据进行了广泛搜集,共得到132篇正丙醇黏度实验数据文献,共包含538个实验数据,其中7篇文献包含高压状态下的实验数据,3篇文献包含 0.1 MPa下气相实验数据,其余数据均为常压液相实验数据。然而并非所有数据都可以用于方程开发,不同作者、不同年代、不同的实验方法得到的实验数据相互之间存在较大差异,因此需要对实验数据进行有效评价,筛选出可靠的黏度实验数据用于方程的开发。本文将搜集到的黏度实验数据分为了两类:第一类是基本数据,这类数据用于方程的开发;第二类数据主要用于方程的检验。数据的筛选遵循以下原则[1]:(1)文献中黏度实验测量方法具备完善的工作方程,并且其中的相关参数能够通过标定或者实验测量得到;(2)文献中应包含实验所用样品的纯度信息;(3)文献中应给出实验数据的不确定度分析。此外,还需考虑实验数据的温度、压力范围,应尽可能拓展方程的适用范围。
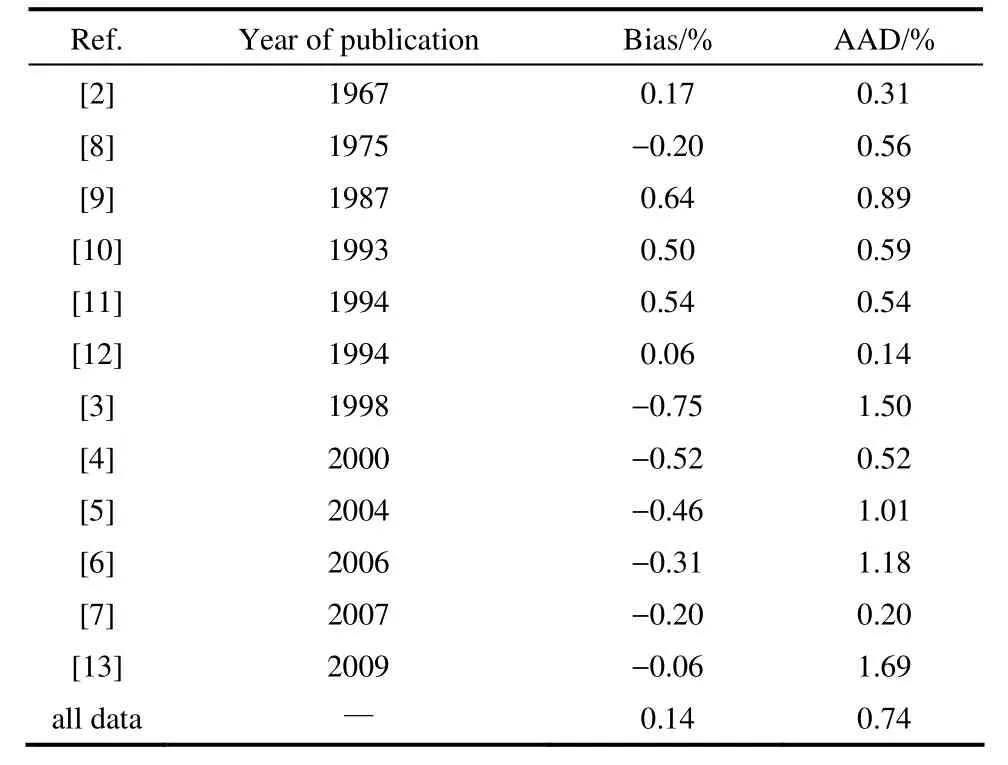
按照以上数据筛选原则,对132篇文献中正丙醇的黏度实验数据进行了详细分析和评价。在常压实验数据筛选中,选取了温度覆盖范围较广、精度较高的6 篇文献实验数据作为基本数据[2-7]。其中,Komarenko等[2]的实验温度范围为153~298 K,其最低温度接近三相点温度。Kumagai等[3]、Tu等[4]、Saleh等[5]、Yang等[6]和 Pang等[7]采用了毛细管黏度计,测量温度范围为273~363 K,测量不确定度大部分小于 1%。高压黏度实验数据[8-13],Weber[8]的实验方法为滚球黏度计,实验压力范围为 0.1~49.1 MPa,温度范围为 273~373 K,不确定度为1.5%。Tanaka等[9]的实验方法为落体黏度计,实验压力范围为0.1~117.8 MPa,温度范围为283~323 K,不确定度为2%。Papaioannou等[10]、Assael等[11]的实验方法为落体黏度计,实验压力范围分别为0.1~71.75 MPa和0.1~51.8 MPa,温度为298 K,不确定度小于2.5%。Papaioannou等[12]的实验方法为振动弦黏度计,实验压力范围为0.1~27.86 MPa,温度范围为 295~328 K,不确定度为 0.5%。Baylaucq等[13]的实验方法为落体黏度计,实验压力范围为0.1~100 MPa,温度范围为293~353 K,不确定度为 2%。通过对高压黏度数据的对比,并结合方程的适用范围,本文选用以上6篇文献高压实验数据作为基本数据。最终用于正丙醇黏度方程开发的实验数据包括12篇文献,共计178个数据点,表1给出了基本实验数据相关信息。


表1 正丙醇黏度基本实验数据Table 1 Primary data used in developing viscosity correlation of n-propanol

表2 密度方程式(1)~式(4)的系数Table 2 Coefficients for Eq. (1) to Eq.(4)

2 黏度方程形式
根据现有黏度理论研究和已有黏度方程开发经验[19-24],纯质黏度的计算以温度和密度为自变量,并由四项互相独立的项组成。

式中,η0(T)为零密度项;η1(T)ρ为初始密度依赖项,通常认为在0.2 MPa内黏度和密度之间是线性关系[23];Δηc(ρ,T)为临界增强黏度项,作用是修正黏度在临界点附近区域的奇异现象,已有文献研究表明[19-24],对于黏度仅在临界点温度1%~2%范围内,Δηc/η可能超过0.01。此外,鉴于所搜集的黏度实验数据中没有近临界区的实验数据,无法开发准确的临界增强型表达式,参考已有文献研究,本文采用了同样的办法,将该项设为零。Δη(ρ,T)为剩余黏度项,该项几乎没有理论指导,其形式主要是参考已有黏度模型并结合实验数据得到。
2.1 零密度项和初始密度依赖项
该项的主要理论基础为分子运动理论,为了更准确地复现实验数据,本文采用了Chung等[25]提出的修正模型,该模型引入了参数Fc用于修正分子结构、分子极性和缔合性质对正丙醇黏度的影响。零密度下的黏度计算方程如式(6)~式(10)所示。
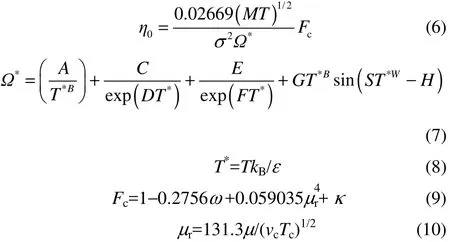
式(6)~式(10)中需要确定的关键参数为势能尺度特征参数σ和势能能量特征参数ε/kB,确定方法分为两种,一种为关联临界参数[25],另一种为关联实验数据进行求解,本文采用了后者。因没有搜集到正丙醇在极低密度下的黏度实验数据,故无法通过推导得到零密度下气体的黏度值,本文将η0(T)+η1(T)ρ作为低密度黏度项与Titani[26]的实验数据相关联,并结合Golubev等[27]的密度实验数据,回归得到σ和ε/kB。式(6)~式(10)中的相关参数、系数和指数见表3。
文献研究表明,无论是极性还是非极性物质,在一定温度范围内,低压下气体的黏度会沿等温线随密度的增加而降低,这种现象可以通过第二黏度维里系数进行量化说明,其主要理论依据为Rainwater and Friend 理论[28-30],并可由式(1)关联得到。

为了方便与实验数据进行对比,引入量纲1第二黏度virial系数B*η(T),该系数与温度的关系式由文献[31]给出,其温度适用范围为 0.3 式中,NA为Avogadro常数,式(13)中的相关系数见表3。 剩余黏度项形式的选择,需要考虑黏度在高密度区域的数量级变化特性以及方程的外推性等因素,结合正丙醇的黏度特性并参考已有黏度方程研究[19-24],最终确定剩余黏度项的形式如下 表3 式(6)~式(13)中的系数Table 3 Coefficients for Eq. (6) to Eq.(13) 表4 剩余黏度项系数和指数Table 4 Coefficients and parameters for Eq. (14) 其中,Δη(ρ,T)的单位为 μPa⋅s,ρr=ρ/ρc,Tr=T/Tc。由于基本实验数据的不确定度不尽相同,因此需要对不同的实验数据进行权重设置,初始权重采用不确定度平方分之一进行设置,即w=1/(ηu)2。对于不确定度不明确的黏度实验数据,参考其实验方法、发表年代和样品纯度信息等进行初始权重设置。通过合理的权重设置,最终得到的拟合结果如表4所示。 表5给出了黏度文献实验数据与开发的方程计算值偏差情况,方程很好地复现了实验数据,其基本实验数据与方程计算值的平均偏差(Bias)为0.14%,平均绝对偏差(AAD)为 0.74%(Bias和AAD计算方法与密度一样),最大偏差为-5.02%。 下述实验数据分析来自于文献[2-13,33-50]。图1给出了0.1 MPa下温度范围为153~363 K的液相黏度实验数据与方程的计算值之间的偏差,图2给出在压力范围为 0.1~117.8 MPa,温度范围为273~373 K下的实验数据与方程计算值间的偏差随密度变化的分布,从图中可以看出偏差基本在±2.5%以内,且均匀分布在正负两侧,没有明显的趋势走向。 表5 正丙醇黏度方程相关统计指标Table 5 Evaluation of n-propanol viscosity correlation for primary data 在常压状态下,Komarenko等[2]的实验数据的温度范围为153~298 K,黏度在低温区域随着密度的增加会呈现出数量级的变化,方程很好地复现了这种特性,实验数据与计算值的Bias为0.17%,AAD为0.31%;Yang等[6]的实验数据与方程的计算值的AAD为1.18%,与其不确定度相当;Pang等[7]的实验数据与方程的计算值的 AAD为 0.20%,在其不确定度0.4%以内。在高压黏度实验数据中,Tanaka等[9]的实验数据与方程的计算值的AAD为0.89%,在其不确定度 2%内;Baylaucq等[13]的实验数据与方程的计算值的AAD为1.69%,在其不确定度2%内。根据实验数据范围,最终方程可适用于温度范围为150~400 K,压力范围为0.1~120 MPa的状态区域内。150~373 K、0.1 MPa范围内方程的不确定度为1%,273~373 K、压力120 MPa以内方程的不确定度估计为 2%,其他区域根据范围不同估计不确定度为2%~5%。 图1 正丙醇常压下液相黏度实验数据与计算值偏差Fig.1 Percentage deviations of primary data at 0.1 MPa for n-propanol 图2 正丙醇高压下液相黏度实验数据与计算值偏差Fig.2 Percentage deviations of primary data at high pressure for n-propanol 图3为方程在不同等温线下黏度与密度的曲线,由图可以发现黏度的变化曲线平滑,为混合物黏度的预测奠定了基础。表6给出了不同温度和密度下方程的计算值,以便实际应用中方程的检验。 在第二类数据中,张建侯等[33]测量了298.15 K下压力范围为0.1~29.5 MPa的正丙醇黏度,其实验数据与计算值的Bias为1.50%,AAD为1.54%,虽然偏差不算太大,但该温度下偏差随压力变化存在系统偏差。在剩余的第二类数据中,部分数据与其他数据有着明显的偏差,例如 Mokhtarani等[34]采用滚球式黏度计测量了常压下温度范围为 283~333 K的正丙醇黏度,其实验数据与计算值的偏差从 7.6%增大到 17.6%;Kermanpour等[35]采用了毛细管黏度计测量了温度范围为293~333 K的正丙醇黏度,其实验数据与计算值的最大偏差为-52%,结果明显存在错误。为了验证方程的合理性,对于第二类数据首先排除了与其他实验数据有明显偏差的文献实验数据,并选择包含5个以上实验数据的文献[36-53]与方程计算值进行了对比,结果如图4所示,第二类数据偏差基本在±5%以内,整体AAD为1.99%,Bias为-0.28%,证明所拟合的正丙醇黏度方程能够很好地复现实验数据。 图3 正丙醇黏度沿不同等温线随密度的变化曲线Fig.3 Viscosity of n-propanol as a function of density along isotherms 表6 正丙醇黏度方程计算验证值Table 6 Sample points for computer verification of correlating equations 图4 第二类数据0.1 MPa下液相黏度实验值与计算值偏差Fig.4 Percentage deviations of the secondary data 本文对正丙醇公开发表的黏度文献实验数据进行全面搜集和整理,对文献中的黏度实验数据进行了评价和筛选,利用筛选出的基本数据开发了宽范围高精度正丙醇黏度方程,基本实验数据与方程计算值的平均绝对偏差为 0.74%。方程的温度适用范围为 150~400 K,压力适用范围为 0.1~120 MPa,在适用范围内估计不确定度为 1%~5%。本文所开发的正丙醇黏度方程不仅很好地复现了实验数据,而且具有合理的外推特性。 符 号 说 明 Bη——第二黏度 virial系数,m3⋅kg-1 M——物质的摩尔质量,g⋅mol-1 NA——Avogadro常数 p——压力,MPa T——热力学温度,K T*——对比温度 Tc——临界温度,K Tr——临界对比温度 vc——临界比体积,cm3⋅mol-1 η——动力黏度,μPa·s ηc——临界黏度增强项,μPa·s η0——稀薄气体黏度,μPa·s η1——密度线性相关项,μPa·s·m3·kg-1 Δη——剩余黏度,μPa·s κ——经验性缔合参数 μ——偶极矩,D μr——对比偶极矩 ρ——密度,kg⋅m-3 ρc——临界密度,kg⋅m-3 ρr——临界对比密度 Ω*——分子碰撞积分 ω——偏心因子 下角标 exp ——实验值 cal ——计算值 [1] ASSAEL M J, RAMIRES M, NIETO DE CASTRO C A,et al.Benzene: a further liquid thermal conductivity standard[J]. Journal of Physical and Chemical Reference Data, 1990, 19(1): 113-117. [2] KOMARENKO V G, MANZHELII V G, RADTSIG A V. Density and viscosity of normal alcohols at low temperatures[J]. Ukrainian Physical Journal, 1967, 12: 676. [3] KUMAGAI A, YOKOYAMA C. Liquid viscosity of binary mixtures of methanol with ethanol and 1-propanol from 273.15 to 333.15 K[J].International Journal of Thermophysics, 1998, 19(1): 3-13. [4] TU C H, LIU C Y, WANG W F,et al. Volumetric and viscometric properties of binary mixtures of aliphatic alcohols (C1-C4) with nitroethane from 293.15 K to 313.15 K[J]. Journal of Chemical and Engineering Data, 2000, 45(3): 450-456. [5] SALEH M A, AKHTAR S, BEGUM S,et al. Density and viscosity of 1-alkanols[J]. Physics and Chemistry of Liquids, 2004, 42(6):615-623. [6] YANG C S, LAI H X, LIU Z G,et al. Density and viscosity of binary mixtures of diethyl carbonate with alcohols at (293.15 to 363.15) K and predictive results by UNIFAC-VISCO group contribution method[J]. Journal of Chemical and Engineering Data, 2006, 51(4):1345-1351. [7] PANG F M, SENG C E, TENG T T,et al. Densities and viscosities of aqueous solutions of 1-propanol and 2-propanol at temperatures from 293.15 K to 333.15 K[J]. Journal of Molecular Liquids, 2007, 136(1):71-78. [8] WEBER W. Über die druckabhängigkeit der viskosität von alkohol-wasser-gemischen[J]. Rheologica Acta, 1975, 14(11):1012-1025. [9] TANAKA Y, MATSUDA Y, FUJIWARA H,et al. Viscosity of(water+alcohol) mixtures under high pressure[J]. International Journal of Thermophysics, 1987, 8(2): 147-163. [10] PAPAIOANNOU D, BRIDAKIS M, PANAYIOTOU C G. Excess dynamic viscosity and excess volume ofn-butylamine + 1-alkanol mixtures at moderately high pressures[J]. Journal of Chemical and Engineering Data, 1993, 38(3): 370-378. [11] ASSAEL M J, POLIMATIDOU S K. Measurements of the viscosity of alcohols in the temperature range 290—340 K at pressures up to 30 MPa[J]. International Journal of Thermophysics, 1994, 15(1): 95-107. [12] PAPAIOANNOU D, PANAYIOTOU C. Viscosity of alkanol + alkane mixtures at moderately high pressures[J]. Journal of Chemical and Engineering Data, 1994, 39(3): 463-466. [13] BAYLAUCQ A, WATSON G, ZÉBERG-MIKKELSEN C K,et al.Dynamic viscosity of the binary system 1-propanol+ toluene as a function of temperature and pressure[J]. Journal of Chemical and Engineering Data, 2009, 54(9): 2715-2721. [14] ZAKHARYAEV Z R. Experimental observation ofpVTproperties of 1-propanol[J]. Inzh.-Fiz. Zh, 1982, 43(3): 796-798. [15] ZÚÑIGA-MORENO A, GALICIA-LUNA L A. Densities of 1-propanol and 2-propanolviaa vibrating tube densimeter from 313 to 363 K and up to 25 MPa[J]. Journal of Chemical and Engineering Data, 2002, 47(2): 155-160. [16] KITAJIMA H, KAGAWA N, ENDO H,et al. Isochoric heat capacities of alkanols and their aqueous mixtures[J]. Journal of Chemical and Engineering Data, 2003, 48(6): 1583-1586. [17] WATSON G, LAFITTE T, ZÉBERG-MIKKELSEN C K,et al.Volumetric and derivative properties under pressure for the system 1-propanol + toluene: a discussion of PC-SAFT and SAFT-VR[J].Fluid Phase Equilibria, 2006, 247(1): 121-134. [18] DÁVILA M J, ALCALDE R, ATILHAN M,et al.pρTmeasurements and derived properties of liquid 1-alkanols[J]. Journal of Chemical Thermodynamics, 2012, 47(3): 241–259. [19] VOGEL E, HERRMANN S. New Formulation for the viscosity of propane[J]. Journal of Physical and Chemical Reference Data, 2016,45(4): 043103. [20] CAO F L, MENG X Y, WU J T,et al. Reference correlation of the viscosity of meta-xylene from 273 to 673 K and up to 200 MPa[J].Journal of Physical and Chemical Reference Data, 2016, 45(1):013103. [21] VOGEL E, SPAN R, HERRMANN S. Reference correlation for the viscosity of ethane[J]. Journal of Physical and Chemical Reference Data, 2015, 44(4): 043101. [22] BALOGUN B, RIESCO N, VESOVIC V. Reference correlation of the viscosity of para-xylene from the triple point to 673 K and up to 110 MPa[J]. Journal of Physical and Chemical Reference Data, 2015,44(1): 013103. [23] AVGERI S, ASSAEL M J, HUBER M L,et al. Reference correlation of the viscosity of toluene from the triple point to 675 K and up to 500 MPa[J]. Journal of Physical and Chemical Reference Data, 2015,44(3): 033101. [24] AVGERI S, ASSAEL M J, HUBER M L,et al. Reference correlation of the viscosity of benzene from the triple point to 675 K and up to 300 MPa[J]. Journal of Physical and Chemical Reference Data, 2014,43(3): 033103. [25] CHUNG T H, AJLAN M, LEE L L,et al. Generalized multiparameter correlation for nonpolar and polar fluid transport properties[J].Industrial and Engineering Chemistry Research, 1988, 27(4):671-679. [26] TITANI T. The viscosity of vapours of organic compounds(PartⅢ)[J]. Bulletin of the Chemical Society of Japan, 1933, 8(9): 255-276. [27] GOLUBEV I F, VASIL'KOVSKAYA T N, ZOLIN V S. Density of propyl and isopropyl alcohols at various temperatures and pressures[J]. Trudy GIAP, 1979, 54(5): 5-15. [28] RAINWATER J C, FRIEND D G. Second viscosity and thermal-conductivity virial coefficients of gases: extension to low reduced temperature[J]. Physical Review A, 1987, 36(8): 4062. [29] RAINWATER J C. On the phase space subdivision of the second virial coefficient and its consequences for kinetic theory[J]. The Journal of Chemical Physics, 1984, 81(1): 495-510. [30] FRIEND D G, RAINWATER J C. Transport properties of a moderately dense gas[J]. Chemical Physics Letters, 1984, 107(6):590-594. [31] VOGEL E, KUECHENMEISTER C, BICH E,et al. Reference correlation of the viscosity of propane[J]. Journal of Physical and Chemical Reference Data, 1998, 27(5): 947-970. [32] POLING B E, PRAUSNITZ J M, O'CONNELL J P. The properties of gases and liquids[M]. 5th ed. New York: McGraw-Hill, 2001. [33] 张建侯, 刘洪勤. 有机物质粘度的加压测定和高压液体粘度与密度的关联方程[J]. 化工学报, 1991, 42(3): 269-277.ZHANG J H, LIU H Q. Determination of viscosity under pressure for organic substances and its correlation with density under high pressure[J]. Journal of Chemical Industry and Engineering(China),1991, 42(3): 269-277. [34] MOKHTARANI B, SHARIFI A, MORTAHEB H R,et al. Density and viscosity of 1-butyl-3-methylimidaz-olium nitrate with ethanol,1-propanol, or 1-butanol at several temperatures[J]. The Journal of Chemical Thermodynamics, 2009, 41(12): 1432-1438. [35] KERMANPOUR F, NIAKAN H, SHARIFI T. Density and viscosity measurements of binary alkanol mixtures from (293.15 to 333.15) K at atmospheric pressure[J]. Journal of Chemical and Engineering Data,2013, 58(5): 1086-1091. [36] MIKHAIL S Z, KIMEL W R. Densities and viscosities of 1-propanol-water mixtures[J]. Journal of Chemical and Engineering Data, 1963, 8(3): 323-328. [37] RAUF M A, STEWART G H, FARHATAZIZ. Viscosities and densities of binary mixtures of 1-alkanols from 15 to 55℃[J]. Journal of Chemical and Engineering Data, 1983, 28(3): 324-328. [38] PAEZ S, CONTRERAS M. Densities and viscosities of binary mixtures of 1-propanol and 2-propanol with acetonitrile[J]. Journal of Chemical and Engineering Data, 1989, 34(4): 455-459. [39] GARCIA B, HERRERA C, LEAL J M. Shear viscosities of binary liquid mixtures: 2-pyrrolidinone with 1-alkanols[J]. Journal of Chemical and Engineering Data, 1991, 36(3): 269-274. [40] SALEH M A, UDDIN M H. Viscosity and thermodynamics of viscous flow of the systems, 1-propanol + formamide, +N-methylformamide, +N,N-dimethylformamide[J]. Physics and Chemistry of Liquids, 1999, 37(6): 701-718. [41] SALEH M A, BEGUM S, UDDIN M H. Viscosity and thermodynamics of viscous flow of 1-propanol with aniline,N-methylaniline andN,N-dimethylaniline[J]. Physics and Chemistry of Liquids, 2001, 39(4): 465-480. [42] BHUIYAN M, FERDAUSH J, UDDIN M. Densities and viscosities of binary mixtures of {dimethylsulfoxide+ aliphatic lower alkanols(C1—C3)} at temperatures fromT=303.15 K toT=323.15 K[J]. The Journal of Chemical Thermodynamics, 2007, 39(5): 675-683. [43] NAIN A K. Ultrasonic and viscometric studies of molecular interactions in binary mixtures of formamide with ethanol, 1-propanol,1, 2-ethanediol and 1, 2-propanediol at different temperatures[J].Journal of Molecular Liquids, 2008, 140(1): 108-116. [44] DOMANSKA U, LASKOWSKA M. Temperature and composition dependence of the density and viscosity of binary mixtures of{1-butyl-3-methylimidazolium thiocyanate+ 1-alcohols}[J]. Journal of Chemical and Engineering Data, 2009, 54(7): 2113-2119. [45] RANJBAR S, FAKHRI K, GHASEMI J B. Densities and viscosities of (1-propanol + 1,2-dichloroethane), (1-propan-ol + benzaldehyde),(benzaldehyde + 1,2-dichloroethane), and (1-propanol +1,2-dich-loroethane + benzaldehyde) mixtures fromT=288.15 K to 313.15 K[J]. Journal of Chemical and Engineering Data, 2009, 5(12):3284-3290. [46] YAN J H, DAI L Y, WANG X Z,et al. Densities and viscosities of binary mixtures of cyclopropanecarboxylic acid with methanol,ethanol, propan-1-ol, and butan-1-ol at different temperatures[J].Journal of Chemical and Engineering Data, 2009, 54(3):1147-1152. [47] HAN S, ZHU C, MA Y. Densities and viscosities of naphthalen-1-ol,naphthalen-2-ol, and 1-aminonaphthalene in the solvents of ethanol,propan-1-ol, and butan-1-ol[J]. Journal of Chemical and Engineering Data, 2012, 57(5): 1396-1403. [48] QIAN W, XU Y, ZHU H,et al. Properties of pure 1-methylimidazolium acetate ionic liquid and its binary mixtures with alcohols[J]. The Journal of Chemical Thermodynamics, 2012, 49(3):87-94. [49] XU Y, YAO J, WANG C,et al. Density, viscosity, and refractive index properties for the binary mixtures ofn-butylammonium acetate ionic liquid+ alkanols at several temperatures[J]. Journal of Chemical and Engineering Data, 2012, 57(2): 298-308. [50] ESTRADA-BALTAZAR A, IGLESIAS-SILVA G, CABALLEROCERÓN C. Volumetric and transport properties of binary mixtures ofn-octane + ethanol, + 1-propanol,+ 1-butanol, and + 1-pentanol from(293.15 to 323.15) K at atmospheric pressure[J]. Journal of Chemical and Engineering Data, 2013, 58(12): 3351-3363. [51] KIJEVČANIN M L, ŽIVKOVIĆ E M, DJORDJEVIĆ B D,et al.Experimental determination and modeling of excess molar volumes,viscosities and refractive indices of the binary systems(pyridine+1-propanol, + 1,2-propanediol, + 1,3-propanediol, and +glycerol). New UNIFAC-VISCO parameters determination[J]. The Journal of Chemical Thermodynamics, 2013, 56(1): 49-56. [52] KERMANPOUR F, SHARIFI T. Measurement and correlation of the excess properties of ternary mixture of {x1[Hmim][BF4] +x21-propanol +x32-propanol} at different temperatures[J]. Journal of Chemical and Engineering Data, 2014, 59(6): 1922-1929. [53] ZHU C, HAN S, LIU J,et al. Densities and viscosities of diaminotoluene with water, ethanol, propan-1-ol, and butan-1-ol from(293.15 to 333.15) K[J]. Journal of Chemical and Engineering Data,2014, 59(3): 880-889. date:2017-03-30. MENG Xianyang, associate professor,xymeng@ mail.xjtu.edu.cn supported by the National Natural Science Foundation of China (51676159) and the Natural Science Basic Research Plan in Shaanxi Province of China (2015JM5214). Correlation of viscosity ofn-propanol MENG Xianyang, YU Ye, WU Jiangtao n-Propanol is widely used in different industries such as pharmaceutical manufacturing and agriculture.The thermophysical properties are the fundamentals for those processes. Viscosity is an important property which influences the design of process equipment, product quality monitoring and so on. However, the experimental data of viscosity are often obtained with discrete points. Correlating equations with these experimental data are prerequisite to use. To author’s best knowledge, there is no such a viscosity correlation forn-propanol available in wide temperature and pressure ranges. The aim of this work is to develop the viscosity correlation ofn-propanol with high accuracy, which can be used over the whole thermodynamic surface. Based on the selected reliable experimental data, the correlation for the viscosity ofn-propanol was presented. The extrapolation behavior of the correlation is reasonable, and the temperature is valid from 150 to 400 K at pressures up to 120 MPa. The estimated uncertainties of this correlation are from 1% to 5%. n-propanol; viscosity; model; thermodynamics TK 121 A 0438—1157(2017)11—4035—08 10.11949/j.issn.0438-1157.20170328 2017-03-30收到初稿,2017-07-17收到修改稿。 联系人及第一作者:孟现阳(1978—),男,副教授。 国家自然科学基金项目(51676159);陕西省自然科学基础研究计划项目(2015JM5214)。
2.2 剩余黏度项



3 实验数据分析




4 结 论

(Key Laboratory of Thermo-Fluid Science and Engineering of Ministry of Education,School of Energy and Power Engineering,Xi’an Jiaotong University,Xi’an710049,Shaanxi,China)

