基于改进的同步扰动随机逼近算法的聚表二元驱优化
张 凯, 张秀清, 张黎明, 张 进, 孙 海, 黄朝琴, 姚 军
(中国石油大学石油工程学院,山东青岛 266580)
基于改进的同步扰动随机逼近算法的聚表二元驱优化
张 凯, 张秀清, 张黎明, 张 进, 孙 海, 黄朝琴, 姚 军
(中国石油大学石油工程学院,山东青岛 266580)
聚表二元驱作为一种提高采收率的有效方法已经被广泛应用于各大油田,为实现聚表二元驱生产效益最大化,从油田实际情况出发,将油田开发的经济效益作为优化目标,选取聚合物与表面活性剂的质量浓度、注入体积、注入时机等参数作为调控变量,并结合改进随机差异化步长的SPSA算法进行优化求解,比较约束与不约束聚合物、表面活性剂使用总量。结果表明:随机差异化步长不仅可以加快算法的运行效率而且能更好地实现全局最优性;当不约束聚合物和表面活性剂使用总量时,在含水率越小时实施聚表二元驱,生产效益越好;当约束聚合物和表面活性剂使用总量时,聚合物和表面活性剂使用总量越小,在含水率越大时实施聚表二元驱生产效益越好。
同步扰动随机逼近算法; 生产优化; 聚表二元驱; 归一化梯度; 随机差异化步长; 最佳注入时机
在油田实际开发中,聚表二元驱是一种提高采收率的生产措施。与水驱相比,聚表二元驱既有聚合物驱的流度控制作用,又有表面活性剂的降低面界面张力的能力,因此聚表二元驱提高原油采收率的效果显著。但目前各大油田关于聚表二元驱的研究仍然停留在聚合物和表面活性剂的注入质量浓度优选上,即配方优选[1-2]。对于不同配方应如何设计注入体积、注入时机才能使效益最大化方面,主要依靠现场人员的施工经验,缺乏相关优化理论的指导。油藏生产优化[3-4]是最早被提出的将油藏数值模拟器与最优化算法相结合的方法,它将经济净现值(NPV)作为目标函数,油水井的注采量作为可调变量,结合优化算法进行优化,使开发处于最佳状态。目前,研究较多的算法有遗传算法[5-6]、人工蜂群算法[7-8]、粒子群算法[9]、同时扰动随机逼近算法等。同步扰动随机逼近算法(SPSA)因为收敛速度相对较快、效率高、时间成本低而应用广泛。Wang等[10]首次将SPSA算法引入到油藏生产优化理论中;赵辉等[11]通过引入变量协方差矩阵对SPSA算法进行改进,提出了一种GSPSA算法,该算法计算简单,且收敛速度快;Zhou等[12]利用SPSA算法与有限差分算法的结合算法,将净现值作为目标函数,聚合物质量浓度、聚合物注入体积作为可调变量,对聚合物驱进行生产优化;Yan等[13]将有限差分近似梯度与随机梯度结合起来,并验证该算法的收敛速度较快;赵辉等[14]通过优化三角阵对敖东梯度进行升级,实现了SPSA算法对真实梯度的逼近。以上研究针对的都是SPSA算法收敛速度的改进,但求解最优化问题的关键是收敛速度和全局最优性,目前关于SPSA算法的全局最优性方面的研究仍然较少。笔者结合人工蜂群算法,对SPSA算法的固定步长进行改进,提出随机差异化步长的方法,并结合归一化梯度处理约束条件,并利用改进的SPSA算法对聚表二元驱优化模型进行优化求解,探究聚合物、表面活性剂使用总量与可调变量之间的普遍关系。
1 聚表二元驱优化模型
在油田实际生产中,通常将生产净现值(NPV)作为评价油田效益的依据。本文中将NPV值作为目标函数。将聚表二元驱的聚合物质量浓度、表面活性剂质量浓度、注入时机、注入体积作为可调变量,建立聚表二元驱优化模型,
(1)
式中,Qo,i,n为第i口生产井第n天的日产油量,m3;Qw,i,n为第i口生产井第n天的日产水量,m3;Qwi,j,n为第j口注水井第n天的日注水量,m3;T为生产时间,d;Np为生产井总数,口;NI为注水井总数,口;cp,j,n为第j口注水井第n天注聚合物的质量浓度,kg/m3;cs,j,n为第j口注水井第n天注表面活性剂的质量浓度,kg/m3;tn为累积计算时间;a为原油的价格,元/m3;b为产出水处理价格,元/m3;c为注水成本,元/m3;e为聚合物的价格,元/kg;f为表面活性剂的价格,元/kg;rate为利率。
约束条件为
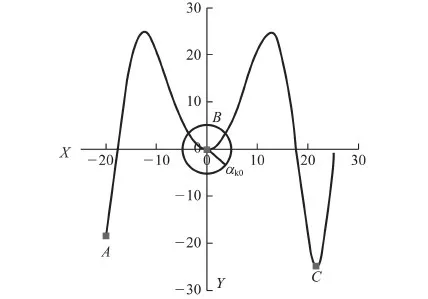
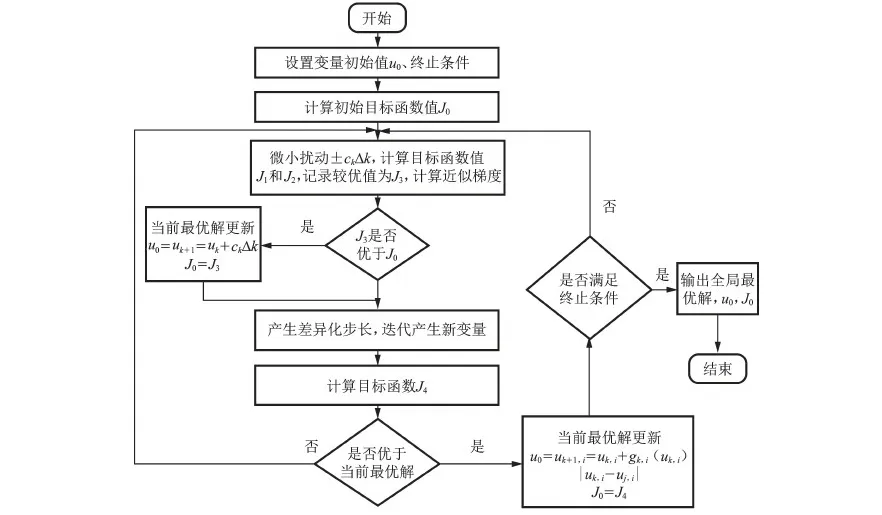
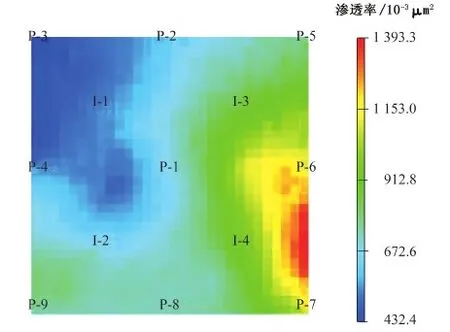
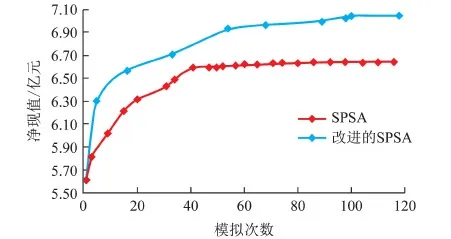
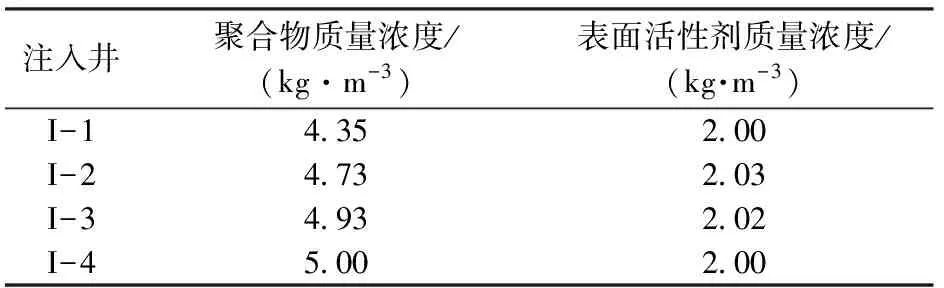
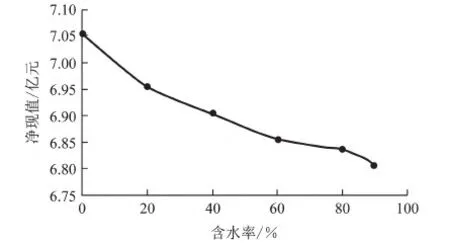
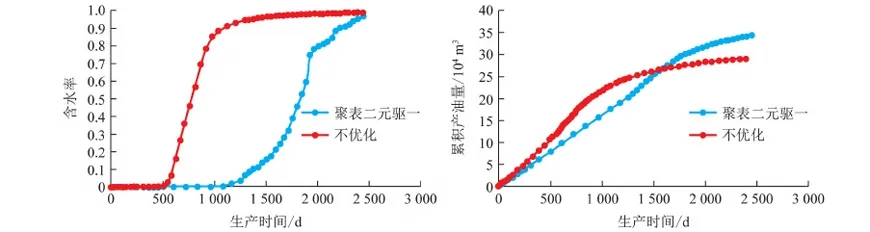
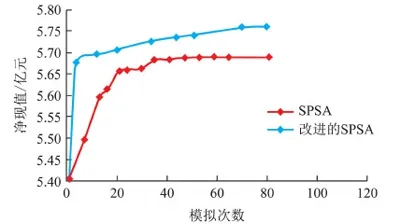
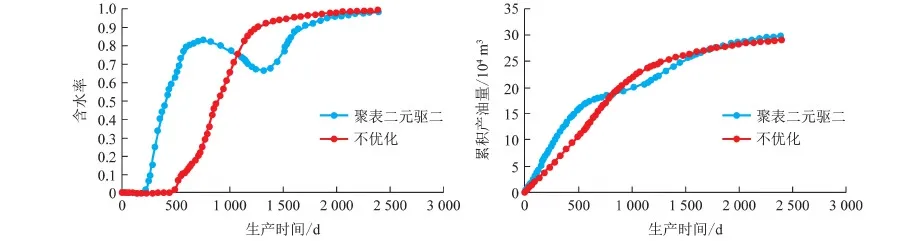
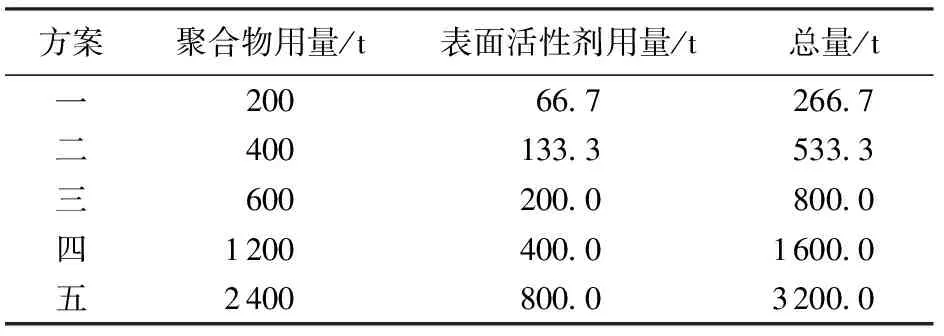
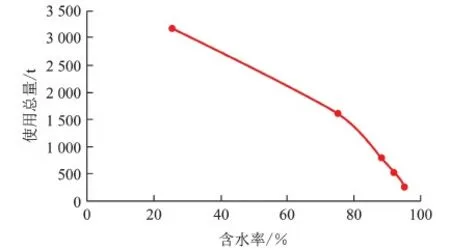
Cp,i,low (2) Cs,i,low (3) Vlow (4) 0 (5) Pamout=C1, (6) Samout=C2. (7) 式中,Cp,i为第i口注水井注聚合物质量浓度;Cp,i,up和Cp,i,low分别为聚合物质量浓度的最大值和最小值;Cs,i为第i口注水井注表面活性剂质量浓度;Cs,i,up和Cs,i,low分别为表面活性剂质量浓度的最大值和最小值;V为段塞的注入体积;Vup和Vlow分别为注入体积的最大值和最小值;N为聚表二元驱的实施时间;Pamout和Samout分别为聚合物和表面活性剂使用总量;C1和C2为常数。 求解最优化问题的关键是优化算法的选取与约束条件的处理。目前,求解最优化问题的算法主要分为两大类,梯度类算法和无梯度类算法。梯度类算法通过求解梯度确定搜索方向,在求解最优化问题时收敛速度快、效率高,但在求解高维问题时,梯度的求解难度大、时间成本高。无梯度算法包括启发式算法、近似梯度算法和插值型算法。随机梯度算法由于搜索方向相对准确、近似梯度求解简单而得到广泛应用。 2.1 模型求解优化算法 SPSA算法是一种有效的梯度近似算法,同时对所有的控制变量扰动,只需一次梯度计算即可得到所有变量的近似梯度方向,大大减少了目标函数的计算次数。虽然计算SPSA近似梯度具有一定的随机性,但是沿该方向总能找到函数值增加的点。同时,随机梯度的期望值是真实梯度方向的近似方向,所以SPSA算法具有收敛速度快、效率高等优点。 2.1.1 SPSA算法 SPSA算法是Spall在有限差分随机逼近(FDSA)算法的基础上改良形成的。FDSA算法以有限差分梯度逼近为基础,每2个目标函数值只能确定一个变量的梯度方向。对于P维问题,至少需2P个目标函数值才能完全确定P个变量的梯度方向。而SPSA算法只需2个目标函数值即可确定所有变量的梯度方向。SPSA算法每次梯度逼近的目标函数值计算次数是有限差分算法的1/P。虽然SPSA算法的近似梯度方向精确性比FDSA算法近似梯度差,但经过Rosenbrock函数的实例测试,SPSA算法求得的近似梯度方向与FDSA算法求得的近似梯度方向夹角始终小于90°。沿SPSA算法求得的近似梯度方向进行搜索,目标函数值总是单调递增或单调递减[15]。 SPSA算法通过同时对所有变量进行微小的扰动ckΔk,求取所有变量的近似梯度方向为 (8) 其中 ck=c/(k+1)γ. 式中,Δk为第k个迭代步的P个[-1,1]之间满足Bernoulli分布的随机数;J为目标函数;uk为第k个迭代步的P个变量组成的矩阵;gk(uk)为第k+1次迭代近似梯度;ck为第k个迭代步的随机扰动步长,随着迭代次数增加而减小;c为初始扰动步长。 求得近似梯度之后,通过式(4)进行迭代,产生新的候选解, uk+1=uk+αkgk(uk). (9) 其中 αk=α/(A+k+1)a. 式中,αk为第k个迭代步的迭代步长;α为初始迭代步长。 标准SPSA方法的计算步骤如下:①给定各个变量的初始值u0、约束条件,给定终止条件,令迭代次数k=0;②根据式(8)、(9)产生{αk}{ck}随机序列及独立同分布且均值为0的P维向量Δk;③求出随机梯度,利用式(8)求近似梯度;④根据公式(9)迭代产生新的值uk+1;⑤重复步骤③~④直到满足收敛条件。 2.1.2SPSA算法的局限性 求解最优化问题的关键是迭代步长和搜索方向。标准SPSA方法的搜索方向与梯度方向的夹角总是小于90°的,所以SPSA算法的收敛速度较快。但标准SPSA算法在实际运用中会出现以下问题。 (1)在每次迭代时,迭代步长为定值,当迭代步长不适时,算法容易陷入局部最优解,全局最优性较差。 根据式(9)可知,迭代步长随迭代次数的增加而减小。当迭代步长较小时,无法跳出局部最优解。如图1所示,在求该函数的极小值时,当寻找到B时,此时步长为αk0,则陷入局部最优解,无法跳出。因此由于步长的限制,SPSA算法的全局最优性较差。 图1 多极值函数Fig.1 More extreme value function (2)每一次迭代时,每一变量的迭代步长一致,忽略了变量约束条件的差异化,降低了算法的效率。从式(9)中可以看出,在特定的迭代次数时迭代步长是一个常数。即对一个P维问题时,每个变量的迭代步长都一样。在实际求解最优化问题时,每个变量的约束条件不同。不同变量的取值范围可能相差较大。如果用统一步长进行迭代,将降低优化的速度。 (3)从标准SPSA的计算方法中可以看出:在每一次变量更新时,都需要3次目标函数值的计算。然而变量更新后的目标函数计算值与梯度微小扰动后的目标函数计算值之间没有进行相关对比。 2.1.3 人工蜂群算法(ABC) ABC算法是基于蜂群行为的启发式智能算法,因全局最优性好而被广泛应用。ABC算法主要包括侦查蜂、引领蜂和跟随蜂。侦查蜂和引领蜂主要负责寻找蜜源,并记录蜜源信息;跟随蜂根据记录信息进行采蜜。当该蜜源被放弃后,引领蜂即转换成跟随蜂,进一步寻找新的蜜源。在优化问题中,蜜源即候选解。当引领蜂找到候选解后,跟随蜂根据式(10)再进一步搜索,寻找更优的候选解, uk+1,d=uk,d+φ(uk,d-uj,d). (10) 式中,uk+1,d为迭代k次的第d维变量更新后的候选解;uk,d为迭代k次时的最优解第d维变量值;φ为[-1,1]之间满足高斯分布的随机数;uj,d为迭代j次时的最优解第d维变量值(j为小于k的随机数)。 2.1.4SPSA算法的改进 针对以上提出的SPSA算法的局限性,分别从步长、优化过程方面对SPSA算法提出了两点改进。 跟随蜂的迭代式(10)与SPSA算法的迭代式(9)相似,uk,d为当前最优解,φ为梯度方向,(uk,d-uj,d)为步长。为了扩大SPSA算法的搜索范围,克服固定步长带来的全局最优性差等缺陷,将ABC算法中跟随蜂的迭代公式中的随机差异化迭代步长(uk,d-uj,d)引入,对SPSA算法的迭代步长进行改进。改进后的迭代式为 uk+1,i=uk,i+gk,i(uk,i)·(uk,i-uj,i). (11) 式中,gk,i(uk,i)为第i维变量迭代第k+1次的近似梯度;uk+1,i和uk,i分别为第i维变量迭代k+1次和k次的值。 步长是随机的,在搜索到全局最优解附近时收敛速度会变慢,在最优解附近来回徘徊。在SPSA算法的优化结构上做了改进:当随机步长寻找到的候选最优解差于随机微小扰动的解时,将微小扰动的解作为当前的全局最优解。这样不仅可以加快算法的收敛速度,而且提高了算法的稳定性。 改进的SPSA算法的优化步骤如图2所示。 图2 改进的SPSA算法的优化流程Fig.2 Improved SPSA algorithm 与标准SPSA算法相比,改进的SPSA算法克服了固定步长的限制,搜索范围不受步长约束,更容易跳出局部最优解,实现全局最优;每一变量的搜索步长不一致,不受固定值约束,收敛速度更快。 2.2 模型约束条件的处理 在该聚合物最优化问题中,约束条件包括不等式和等式约束。等式约束采用传统的拉格朗日乘子法进行处理。针对线性不等式处理,采用归一化梯度和截断法对不等式约束进行简单处理。 对于控制变量u={u1,u2,…,up}∈Rp,其中P为控制变量的维数。每一个变量都须满足以下条件: ui,low≤ui≤ui,up. (12) 式中,ui为第i维变量;ui,up和ui,low分别为第i维变量的最大值和最小值。 在利用式(11)产生新的控制变量uk+1的过程中,由于步长、近似梯度的影响,可能会出现不满足式(12)约束的情况,为了避免这种情况的出现,对近似梯度进行归一化处理,使近似梯度只有方向没有大小, (13) (14) 利用式(11)对变量值进行迭代,然后利用式(14)作简单处理,使迭代后得变量值在约束范围内。 为获得聚表二元驱的最优开发方案,分别采用SPSA算法、改进的SPSA算法对聚表二元驱数学模型进行优化求解。采用Eclipse软件建立数值模型,该模型为1 050 m×1 050 m×2.5 m的非均质两相油藏,采用正五点法井网布井,其中,9口生产井,4口注水井。其渗透率及井位如图3所示。该油藏体积为275.6×104m3,初始地层压力为30 MPa,平均孔隙度为0.29,平均渗透率为753 μm2,原油密度为850 kg/m3,原油黏度为38 mPa·s,初始含油饱和度为0.85。假设每口生产井、注水井分别以120、270 m3/d的速度进行生产,油田生产时间为2 400 d。该模型中4口注水井同时进行聚表二元驱,聚合物、表面活性剂以段塞形式注入,生产方式为水驱-聚表二元驱-后续水驱。 图3 模型的渗透率场以及井位Fig.3 Permeability and well location in model 目标函数中聚合物的价格为20元/kg,表面活性剂为15元/kg,注入水价为0.5元/m3,原油的价格为3 000元/m3,采出水的处理成本为0.5元/m3。 3.1 不约束聚合物和表面活性剂使用总量的聚表二元驱优化模型求解 该实例将聚合物质量浓度、表面活性剂的注入质量浓度、注入时机以及注入体积作为可调变量,进行聚表二元驱生产优化;将聚合物、表面活性剂的注入体积转换为聚合物、表面活性剂的注入时间, T=V/v. (15) 变量约束条件为 0 20 式中,T为聚合物和表面活性剂注入的时间;V为注入体积;v为注入速度。 在不约束聚合物、表面活性剂使用总量的条件下,分别采用SPSA算法、改进的SPSA算法对油田的NPV值进行优化,得到最优生产方案。两种算法的优化结果对比如图4所示。 图4 不约束聚合物和表面活性剂使用总量时两种算法优化结果对比Fig.4 Comparison of optimal result with two different algorithms in aggregate usage of polymer and surfactant without constraint 从图4中可以看出:SPSA算法在模拟73次时找到最优解6.637亿元,改进的SPSA在模拟33次时寻找到的当前最优值6.71亿元,该值高于标准SPSA算法寻找的全局最优解;改进的SPSA在模拟118次时,找到全局最优解7.05亿元;虽然SPSA达到最优值时迭代次数与改进后的算法相差无几,但由于其算法存在局限性,容易陷入局部最优解,所以其寻找到的最优值比改进的SPSA算法小。改进的SPSA算法不仅克服了标准SPSA算法全局最优性差的缺点,而且加快了收敛速度,提高了算法的效率。 优化结果见表1。其中注入时间为1 256 d,1.69倍注入体积,注入时机为开发早期,含水率为0。 从优化结果中可以看出,表面活性剂质量浓度的优化结果约为2 kg/m3。该优化结果与ECLIPSE中表面活性剂的降低界面张力函数一致,在表面活性剂质量浓度为2 kg/m3时界面张力最低,洗油效果最好,洗油效率最高。从聚合物质量浓度的优化结果看,聚合物的使用量靠近约束条件上边界处。从注入时机看,在不约束聚合物、表面活性剂使用总量的条件下,聚表二元驱越早投入生产,开发效果越好。为验证优化结果的准确性,对聚表二元驱的注入时机进行单因素分析,以注入时机为单一变量进行优化。优化结果(为了观察规律,将注入时机与含水率转换)如图5所示。 表1 不约束聚合物和表面活性剂使用总量时生产优化结果Table 1 Optimal results in aggregate usage of polymer and surfactant without constraint 从图5可以看出,在不约束聚合物、表面活性剂使用总量的条件下,最佳注入时机为含水率为0时。 从聚合物、表面活性剂的注入时间中可以看出,聚合物和表面活性剂混合注入1 256 d后停止继续注入。此时,聚表二元驱的优化方案(聚表二元驱一)与不优化的含水率及累积产油量与时间的关系如图6所示。从图6可以看出,当累积注入时间在1 256 d时,整体含水率约为4%。在后续水驱阶段,充分发挥了聚表段塞的后续作用,杜绝了含水率突然增高的情况,达到了增油控水的效果。优化的聚表二元驱方案的驱油效果要明显优于不优化的效果。优化方案在无水采油期采出的油量明显多于不优化方案。 图5 净现值与不同注入时机关系Fig.5 Relationship between NPV value and different injection time 图6 不约束聚合物和表面活性剂使用总量时含水率及累积产油量与时间的关系Fig.6 Relationship between water cut and cumulative production and time in aggregate usage of polymer and surfactant without constraint 3.2 约束聚合物和表面活性剂使用总量的聚表二元驱优化模型求解 出于油田实际情况考虑,将注入聚合物和表面活性剂的成本设置为约束条件,即将聚合物和表面活性剂使用总量作为约束条件,探究聚合物和表面活性剂使用总量固定时聚表二元驱的最优生产方案。模型的约束条件:聚合物使用量为1 200 t,表面活性剂使用量为400 t,其他约束条件与上述模型一致。分别利用SPSA算法、改进的SPSA算法重新对净现值进行优化,优化结果如图7所示。 从图7可以看出,改进后的算法收敛速度快、全局最优性好。改进的SPSA算法优化的油田经济净现值为5.76亿元,远高于SPSA算法优化的经济净现值。改进的SPSA算法优化结果见表2,其中注入时间517 d,0.69倍注入体积,注入时机为生产80 d后注入,此时含水率为75%。 图7 约束聚合物和表面活性剂使用总量时两种算法优化结果对比Fig.7 Comparison of optimal result with two different algorithms in aggregate usage of polymer and surfactant with constraint 注入井聚合物质量浓度/(kg·m-3)表面活性剂质量浓度/(kg·m-3)I-1130102I-2175097I-3206093I-4260100 优化结果认为当聚合物、表面活性剂使用总量受限制时,该油藏模型在注入时聚合物、表面活性质量浓度都受到优化调整。优化的聚表二元驱方案(聚表二元驱二)与不优化方案(生产早期注入聚合物、表面活性剂)的含水率及累积产油量与时间的关系如图8所示。 从图8可以看出,聚表二元驱二方案在开始注入时聚合物与表面活性剂段塞降低含水率的效果比较明显。不优化方案在含水率为0时注入,延缓见水时间,但持续时间短。从注入时机看,约束聚合物和表面活性剂使用总量的优化结果与不约束聚合物和表面活性剂使用总量的优化结果有差异。在聚合物和表面活性剂使用总量不受约束时,注入时机越早越好;当聚合物和表面活性剂的用量分别为1 200和400 t时,注入时机为75%时开发效果较好。不同方案的最佳注入时机与聚合物和表面活性剂用量的关系如表3、图9所示。 图8 约束聚合物和表面活性剂使用总量时含水率及累积产油量与时间的关系Fig.8 Relationship between water cut and cumulative production and time in aggregate usage of polymer and surfactant with constraint 方案聚合物用量/t表面活性剂用量/t总量/t一2006672667二40013335333三60020008000四1200400016000五2400800032000 图9 最佳注入时机与总量的关系Fig.9 Relationship between optimal injection time and usage amount 从图9可以看出,聚表二元驱的最佳注入时机随使用总量的增加而变早,当聚合物、表面活性剂使用总量越大时,在含水率越小时注入聚表二元驱开发效果越好。 (1)差异化随机步长不仅可以加快SPSA算法的收敛速度,而且能克服固定步长带来的缺陷,提高算法的全局最优性。 (2)优化运算时,归一化梯度与差异化随机步长不仅能保证搜索方向的准确性,而且大大简化了约束条件的处理。 (3)当聚合物和表面活性剂使用总量不限制时,聚表二元驱的最佳注入时机为见水之前;当聚合物和表面活性剂使用总量限制时,聚合物和表面活性剂使用总量越小,最佳注入时机在含水率越大处。 [1] 刘平德,张松,杨宁,等.新型表面活性聚合物驱油剂 [J]. 石油勘探与开发,2012,39(5):580-584. LIU Pingde, ZHANG Song, YANG Ning, et al. A novel surface active polymer oil displacement agent [J]. Petroleum Exploration and Development,2012,39(5):580-584. [2] 杨俊茹.交联聚合物微球-聚合物复合调驱注入参数优化设计 [J]. 石油勘探与开发,2014,41(6):727-730. YANG Junru. Injection parameters optimization of cross-linked polymer microspheres and polymer composite flooding system [J]. Petroleum Exploration and Development,2014,41(6):727-730. [3] 张凯,李阳,姚军,等.油藏生产优化理论研究 [J]. 石油学报, 2010,31(1):78-83. ZHANG Kai, LI Yang, YAO Jun, et al. Theoretical research on production optimization of oil reservoirs [J].Acta Petrolei Sinica,2010,31(1):78-83. [4] 赵辉,李阳,康志江.油藏开发生产鲁棒优化方法[J].石油学报,2013,34(5):947-953. ZHAO Hui, LI Yang, KANG Zhijiang, et al. Robust optimization in oil reservoir production [J].Acta Petrolei Sinica,2013,34(5):947-953. [5] PEYMAN B, PEZHMAN K, SEDIGHEH M, et al. A novel approach for modeling and optimization of surfactant/polymer flooding based on genetic programming evolutionary algorithm [J]. Fuel,2016,179:289-298. [6] CLAUDIA G A, ABEL B R, ARTURO J G. Optimization of Petlyuk sequences using a multi objective genetic algorithm with constraints [J]. Computers & Chemical Engineering, 2011,35(2):236-244. [7] SHAMS K N, SALWANI A. An adaptive multi-population artificial bee colony algorithm for dynamic optimization problems [J]. Knowledge-Based Systems,2016,104:14-23. [8] SONG Jingge. Improved artificial bee colony-based optimization of boiler combustion considering NO X emissions,heat rate and fly ash recycling for on-line applications [J]. Fuel,2016,172:20-28. [9] IOAN C T. The particle swarm optimization algorithm: convergence analysis and parameter selection [J]. Information Processing Letters, 2003, 85(6):317-325. [10] WANG Chunhong. Production optimization in closed-loop reservoir management [J].SPE Journal,2009,14(3):506-523. [11] 赵辉,曹琳,李阳,等.基于改进随机扰动近似算法的油藏生产优化 [J]. 石油学报,2011,32(6):1031-1036. ZHAO Hui, CAO Lin, LI Yang, et al. Production optimization of oil reservoirs based on an improved simultaneous perturbation stochastic approximation algorithm [J].Acta Petrolei Sinica,2011,32(6):1031-1036. [12] ZHOU Kang. Optimal control of polymer flooding based on simultaneous perturbation stochastic approximation method guided by finite difference gradient [J]. Computers & Chemical Engineering,2013,55(55):40-49. [13] YAN Xia. Optimization algorithms based on combining FD approximations and stochastic gradients compared with methods based only on a stochastic gradient [J].SPE Journal,2014,19(5):873-890. [14] 赵辉,唐乙玮,康志江,等.油藏开发生产优化近似扰动梯度升级算法[J]. 中国石油大学学报(自然科学版),2016,40(2):99-104. ZHAO Hui, TANG Yiwei, KANG Zhijiang, et al. Reservoir production optimization using an upgraded perturbation gradient approximation algorithm [J]. Journal of China University of Petroleum(Edition of Natural Science),2016,40(2):99-104. [15] 闫霞.基于梯度逼真算法的油藏生产优化理论研究[D]. 青岛:中国石油大学,2013. YAN Xia. Theoretical research of reservoir production optimization based on gradient approximation methods [D].Qingdao:China University of Petroleum,2013. (编辑 李志芬) Anovelapproachforoptimizationofpolymer-surfactantfloodingbasedonsimultaneousperturbationstochasticapproximationalgorithm ZHANG Kai, ZHANG Xiuqing, ZHANG Liming, ZHANG Jin, SUN Hai, HUANG Zhaoqin, YAO Jun (SchoolofPetroleumEngineeringinChinaUniversityofPetroleum,Qingdao266580,China) Polymer-surfactant flooding, as a kind of effective method to enhance oil recovery, has been used in oilfield widely. However, at the current low crude oil price scenarios, how to maximize the production benefit (or project economics) has become an emergent problem to solve. In view of this, in this study, the production benefit was taken as the optimization target, and the polymer and surfactant concentrations, injection volume, injection time were considered as control variables, in order to construct a novel simultaneous perturbation stochastic approximation algorithm, which was improved by a random and differential step method to optimize the production benefit. Two case studies were carried out, with and without restriction on the usage of polymer and surfactant. The simulation results indicate that the improved simultaneous perturbation stochastic approximation algorithm not only can speed up convergence but also can get better optimal result. When the usage amount of polymer and surfactant are not restricted, the production benefits will be better if the polymer and surfactant are injected at lower water cut. When the usage amount of polymer and surfactant are restricted, the production benefits will be better if the polymer and surfactant are injected at higher water cut. simultaneous perturbation stochastic approximation algorithm; production optimization; polymer-surfactant flooding; normalized gradient; random and different step; optimal injection time 2016-12-08 国家自然科学基金项目(51722406,61573018);山东省自然科学基金项目(ZR2015EL014);国家重大专项(2016ZX05025001-006);中央高校基本科研业务费专项(15CX05035A,17CX05002A) 张凯(1980-),男,教授,博士,研究方向为油气田开发。E-mail: reservoirs@163.com。 1673-5005(2017)05-0102-08 10.3969/j.issn.1673-5005.2017.05.012 TE 34 A 张凯,张秀清,张黎明,等.基于改进的同步扰动随机逼近算法的聚表二元驱优化[J].中国石油大学学报(自然科学版),2017,41(5):102-109. ZHANG Kai, ZHANG Xiuqing, ZHANG Liming, et al. A novel approach for optimization of polymer-surfactant flooding based on simultaneous perturbation stochastic approximation algorithm[J].Journal of China University of Petroleum(Edition of Natural Science),2017,41(5):102-109.2 聚表二元驱优化模型求解方法
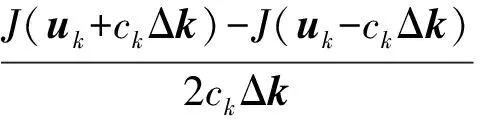
3 实例验证

4 结 论

