基于夹具主动定位补偿的飞机柔性件装配偏差优化方法
张玮, 王志国, 谭昌柏, 刘霞
南京航空航天大学 机电学院, 南京 210016
基于夹具主动定位补偿的飞机柔性件装配偏差优化方法
张玮, 王志国*, 谭昌柏, 刘霞
南京航空航天大学 机电学院, 南京 210016
柔性零件广泛用于航空、汽车等产品中,在柔性件的装配过程中,装配尺寸质量受零件制造、夹具和连接过程中多种偏差源的耦合影响,分析和控制难度大。提出了一种基于夹具主动定位补偿的装配偏差优化方法。首先,基于柔性件装配的受力变形分析,建立了考虑夹具法向定位误差的装配偏差模型。然后,根据上述模型,以夹具法向定位补偿量为优化变量,提出了夹具法向补偿量的优化模型和求解算法。以金属薄板装配和飞机壁板件装配为例,分别利用实验及有限元仿真分析了有无夹具主动定位补偿下的装配偏差。结果表明,夹具法向定位补偿对于减小柔性件的装配偏差具有显著效果,从而验证该优化算法的有效性和准确性。
柔性件装配; 夹具定位; 主动补偿; 装配偏差; 优化
装配偏差是指产品实际装配尺寸相对于设计尺寸的偏离值,装配偏差的产生受到零件制造和装配过程中各种工艺因素的综合影响。柔性件的装配偏差分析与控制是装配尺寸管理的重点和难点。
传统的装配偏差分析都以刚体模型为基础,然而,根据对汽车柔性薄板件装配测量数据的回归研究,Takezawa[1]指出刚体模型已不能适用于柔性件的装配偏差分析。密歇根大学的Liu和Hu[2-4]率先开展了柔性装配偏差分析的研究,将柔性件装配分解成定位、夹紧、焊接及释放回弹四个步骤,在使用有限元分析及统计方法的基础上,提出了影响系数法,通过构建敏感度矩阵建立了输入零件偏差与输出装配体回弹偏差之间的线性关系。针对柔性薄板零件刚性小、易变形的特点,Cai等[5]提出了“N-2-1”的夹具定位策略,通过在柔性件主平面上提供过约束定位(N>3)以减小其变形。相比“3-2-1”定位原则,“N-2-1”定位原则更适用于柔性件装配定位。Hu和Koren[6]在对车身多工位装配工艺研究中,提出“偏差流理论”,用以预测及诊断车身多工位装配系统中的偏差。Hsieh和Kong[7-8]提出了一种以最小装配偏差为目标函数的柔性件装配工艺仿真和优化算法,应用遗传算法进行最小偏差优化。Eimaraghy[9]分析了夹具、焊枪对装配偏差的影响,将钣金件焊接装配分为“3-2-1”完全约束下的刚体运动、夹具定位和焊枪压紧下的变形以及装配约束释放后的回弹变形三个阶段,并建立了装配误差的统一模型。针对多工位柔性装配,Camelio等[10]在影响系数法的基础上,综合零件偏差、夹具偏差及焊枪偏差的影响,研究了偏差在多工位装配过程中的传播。Camelio等[11]又进一步研究了夹具定位对柔性件装配偏差的影响,提出了一种最小化装配偏差的夹具设计方法。田兆青等[12]研究了多工位薄板装配过程中偏差流传递、变换和累积关系的状态空间模型。针对传统分析中公差和维护设计在制造系统中单独考虑的问题,Cui和Zhang[13]建立了集成公差和维护的柔性件多工位装配优化模型。邢彦锋等[14]根据装配后夹具定位点的释放模式不同,建立了过定位释放和完全释放模式下的装配偏差分析模型。Dahlström和Lindkvist[15]考虑装配过程中柔性件的相互接触作用,基于影响系数法建立了柔性装配偏差分析模型。谭昌柏等[16]运用稳健设计方法建立了飞机装配公差的可行稳健性和敏感稳健性两类设计模型。陈晖等[17]针对仅考虑零件几何误差的装配偏差模型不足,结合一阶摄动理论和有限元方法,提出了耦合柔性零件几何和材料误差的装配偏差统计分析方法。针对柔性件装配夹具方面,于奎刚等[18]结合Taguchi方法和柔性薄板装配偏差模型,提出了一种柔性薄板装配夹具稳健设计方法。Cai和Qiao[19]针对飞机钣金装配工艺中刚体和柔性装配同时存在的特点,建立了刚柔混合的装配偏差模型。
夹具定位偏差作为柔性装配系统中装配偏差的重要来源之一,在已有的相关研究中,主要是将夹具定位的误差直接引入柔性装配偏差分析模型,作为装配偏差源考虑,而很少通过主动调节夹具定位去补偿零件制造、定位偏差,以减小最终的装配偏差。本文旨在利用夹具定位对装配的作用,通过科学地建模和计算,在产品装配前主动给夹具定位预设合理的补偿量以减小装配偏差,以期实现对装配偏差的主动控制,改善柔性件的装配质量。
1 引入夹具法向补偿量的柔性件装配偏差建模
柔性件装配可分解为定位、夹紧、装配、释放回弹四个阶段。基于“N-2-1”定位策略,将零件过定位点处的夹具法向定位补偿量作为变量,引入柔性件装配偏差模型,分析装配后的法向偏差。为检验柔性件装配质量,选取部分关键产品特征(Key Product Characteristic,KPC)点作为关键测点,另一方面,在装配过程中,由于装配连接点处变形较大,同时装配连接处的连接质量往往影响整个装配体的质量,本文以装配连接点和KPC点作为关键测点。基于装配中零件的线弹性、小变形假设,分析各装配阶段的柔性件的受力变形。夹具法向定位补偿示意图如图1所示。

图1 夹具法向定位补偿Fig.1 Fixture normal locating compensation
1.1 定 位

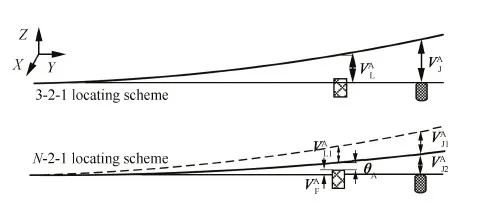
图2 零件A的定位偏差Fig.2 Locating deviation of Part A
在夹具夹紧力作用下,根据有限元方法建立零件变形与受力的关系(以零件A为例)为
(1)

(2)

图3 过约束定位示意图Fig.3 Scheme of over-constrained locating
1.2 夹 紧
柔性零件完成“N-2-1”定位后,通过施加装配压紧力,将零件装配连接点压紧至名义位置。此时,柔性件连接点处受力FJ与装配连接点的变形关系可以表示为
(3)

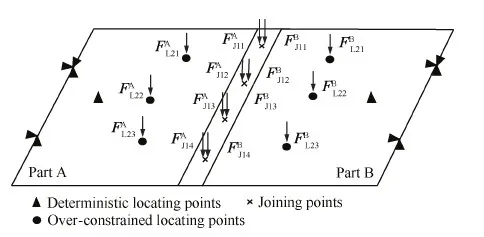
图4 装配前的夹紧力Fig.4 Applying clamping force before joining
此时过定位点受力为
(4)
装配连接点处受力为
(5)
1.3 装 配
柔性件在装配工具的压紧力作用下保持在名义装配位置,通过焊接、铆接等方式连接,形成装配体。对于柔性件连接过程中产生的局部变形及其引起的偏差,本文未予以考虑。
1.4 释放回弹
1) 装配力释放
由于柔性件装配过程中发生变形,装配体内部存在装配应力,释放装配压紧力后,装配体将在内应力的重新平衡过程中发生回弹变形。根据Liu和Hu[2]的一维悬臂梁单元模型,装配应力对零件变形的作用可近似等效为零件装配压紧处与装配力反向的回弹力,结合线弹性、小变形假设,回弹偏差与回弹力FRJ的关系:

(6)

此时装配体过定位点受力为
(7)
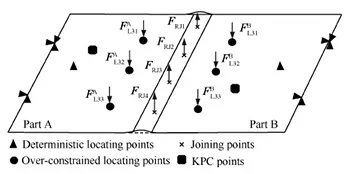
图5 连接点压紧力释放Fig.5 Clamping force release at joining points
2) 夹具过约束点释放
如图6所示,释放夹具过定位点,装配体将进一步回弹变形。基于线弹性、小变形假设,关键点回弹变形偏差和回弹力可以表示为
(8)

装配压紧力和过定位夹具释放后,装配连接点和KPC点的回弹变形偏差分别为
(9)
计算可得
VR=t+mθA+nθB
(10)
VK=s+fθA+gθB
(11)


图6 过约束定位点压紧力释放Fig.6 Clamping force release at over-constrained locating points

(12)
式中:W为系数矩阵;θ为夹具法向定位补偿量;U为不考虑夹具补偿关键测点的装配偏差。
2 面向装配偏差的夹具补偿量优化模型及求解
基于装配偏差模型建立夹具法向补偿量的优化方程,各夹具定位点的法向补偿量θ为优化变量,优化目标可按照以下两种情况来建立。(1)第I类优化目标:当补偿后柔性件关键测点不能保持在理论位置时,此时的优化目标为装配偏差最小,即VTV→min;(2)第II类优化目标:当补偿后柔性件可以保持在理论位置时,为减小调整夹具补偿的工作量,此时的优化目标为夹具法向补偿量最小,即θTθ→min。由于正常情况下夹具的调整量是有限制的,所以夹具的法向定位补偿量需要在给定范围。对该夹具补偿量的二次规划问题进行求解。
令柔性零件A、B过约束点数之和为λ,装配体关键测点(即装配连接点和KPC点)总数为γ,则夹具补偿量为
θ=[θ1θ2…θi…θλ]T
(13)
式中:l≤θi≤u,i=1,2,…,λ(l,u即夹具法向预设的调整范围上、下界)。
2.1 第I类优化目标
当利用夹具定位补偿使得柔性件装配后不能保持在理论位置时,此时的优化目标为装配偏差最小,即VTV→min。则此时过定位点数与关键测点数之间的关系为λ=γ或λ<γ。优化模型如下:
Objective:
minf(θ)=VTV
(14)
Constrains:
l≤θi≤ui=1,2,…,n
(15)
2.2 第II类优化目标
当利用夹具定位补偿,柔性件装配回弹后能保持在理论位置时,此时的优化目标为夹具法向补偿量最小,即θTθ→min。则此时过定位点数与关键测点数之间的关系为λ>γ。故优化模型为
Objective:
ming(θ)=θTθ
(16)
Constrains:
(17)
3 实例验证与分析
以金属薄板装配和某型飞机壁板件装配两个例子来验证本文提出的基于夹具主动定位补偿的柔性件装配偏差优化方法。利用提出的优化算法计算出夹具法向定位补偿量,并将定位补偿量引入实例分析,得到夹具法向定位补偿后的装配偏差值;最后,对比无夹具补偿时的装配偏差数值,验证本文的优化方法。
3.1 金属薄板装配
实例采用实验验证方法,设计铝合金薄板A、B搭接装配实验。铝板A、B材料为6061,弹性模量68.9 GPa,泊松比为0.330,两者尺寸均为400 mm×400 mm,厚度为1 mm。在Abaqus中创建对应有限元模型,划分网格,单元类型为“S4R”,定位点、装配连接点及关键测点位置如图7 所示。其中,D11~D23为确定性定位点,P11~P22为过约束定位点,J1~J3为装配连接点,K11~K22为KPC点。铝板A、B的边界条件如表1所示。利用立体视觉系统测量过定位点及装配连接点初始偏差,如表2所示。

图7 铝板装配有限元模型Fig.7 Finite element model for aluminum sheet assembly

表1 装配边界条件Table 1 Boundary condition of assembly

表2 铝板A、B初始偏差Table 2 Initial deviation of aluminum sheet A and B
铝板装配实验如图8所示,首先铝板A、B利用两孔完成确定性定位,然后利用过定位夹头进行过约束定位。夹头均采用M10螺杆结构,可以通过旋转调节定位高度(Z向)。夹具夹头采用对顶形式,下部为定位夹头,上部为夹紧夹头,示意图如图9所示。夹紧过程利用装配连接处的夹紧夹头将装配连接点压紧至名义位置。利用螺栓连接代替铆接完成装配操作。最后释放装配处压紧夹头以及过约束压紧夹头,装配体发生回弹变形。设计两组实验,第一组不考虑夹具补偿,第二组引入夹具主动定位补偿。利用双目立体视觉系统分别测量两组实验关键测点的位置信息,从而得到其对应的装配偏差。

图8 铝板装配实验Fig.8 Layout experiment of aluminum sheet assembly

图9 夹紧和夹具夹头Fig.9 Clamping and locating fixtures
如图7所示,铝板A、B上过约束定位点数之和λ=4,关键测点数γ=7,则此时的优化目标为装配偏差最小,即VTV→min。结合夹具实际情况,给定夹具定位补偿量的范围为-1.5 mm≤θi≤1.5 mm,i=1,2,3,4。根据已建立的夹具补偿优化算法,求解夹具法向定位补偿量为θ=[1.473 0.57 1.059 0.932]T。将夹具补偿量引入铝板装配实验,根据M10螺纹螺距即可求得过定位夹头需要旋转的角度,旋转定位夹头以进行夹具补偿,实现夹具法向定位补偿。根据夹具补偿量调整过定位处定位夹头,完成装配操作,得到补偿后的回弹装配偏差。对比无夹具补偿时的装配偏差,结果如表3所示。
根据表3实验结果,铝板A、B装配关键测点平均绝对偏差为0.968 mm,调整过定位处定位夹头,补偿后关键测点的平均绝对偏差为0.456 mm。对比各关键测点补偿前后装配偏差及平均绝对偏差可知,利用夹具定位补偿方法减小了装配偏差,验证了夹具主动定位补偿优化方法的工程可行性。

表3 补偿前后的薄板法向偏差对比Table 3 Normal deviation of sheet metal before and after compensation
3.2 飞机壁板件装配
壁板件是构成飞机气动外形的主体结构,具有结构尺寸大,刚度低,制造和装配准确度要求高等特点,且其装配准确度直接影响后续部装和总装的装配质量,对其装配偏差进行分析进而提高装配质量具有重要意义[20]。壁板件是典型的柔性铆接结构,装配中需要用到大量夹具,采用过约束定位方式,以减小装配变形。本案例的分析对象为某型飞机的壁板件,其简化模型如图10所示,其中内型卡板由固定托架及可调定位块组成。夹具的法向定位补偿可利用激光跟踪仪对定位块进行调整实现。结合本文的定位补偿算法,可计算出定位块补偿量。
在Abaqus中建立壁板件有限元分析模型,为简化有限元仿真模型并降低装配仿真的计算量,本文取2张蒙皮、3个内型卡板、5根长桁、5个角片进行装配分析。蒙皮A、B理论曲率半径为1 985 mm,实际曲率半径分别为1 990 mm,1 995 mm。蒙皮、长桁、角片材料均为铝锂合金,弹性模量E=7.3×104N/mm2,泊松比ν=0.3。从突出本文研究重点考虑,本例未考虑长桁、角片的制造偏差以及夹具定位偏差。建立如图11所示仿真模型,其中,D11~D23为确定性定位点,P11~P26为过约束定位点,J1~J5为装配连接点,K11~K22为KPC点,其具体边界条件如表4所示,其中Z*表示的方向为对应蒙皮节点理论位置的法向。

图10 飞机壁板件装配简化模型 Fig.10 Simplified model for aircraft fuselage panel assembly
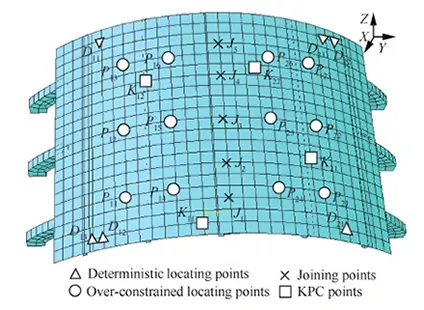
图11 飞机壁板件有限元分析模型Fig.11 FEA model for aircraft fuselage panel

表4 壁板件装配蒙皮边界条件Table 4 Boundary condition of skin in panel assembly
如图11所示,壁板件中蒙皮A、B过约束定位点数之和λ=12,关键测点数γ=9,故此时的优化目标为夹具法向补偿量最小,即θTθ→min。给定卡板定位块的补偿范围为-1.5 mm≤θi≤1.5 mm,i=1,2,…,12。根据优化算法分别求解出夹具Y和Z方向的调整量,合成得到对应卡板定位块法向的补偿量为θ=[0.503 1.236 0.465 -0.654 -0.223 -0.25 0.986 1.762 0.633 0.111 -0.064 -0.182]T。将夹具补偿量引入有限元模型,得到补偿后的壁板件蒙皮法向装配偏差,与无夹具补偿下的装配偏差进行对比,结果如表5所示。
根据表5的计算结果,壁板件装配后蒙皮关键测点法向的平均绝对偏差为0.584 mm,而根据法向定位补偿优化算法,调整卡板定位块并仿真得到蒙皮关键测点法向平均绝对偏差为0.138 mm。对比补偿前后的壁板件装配的蒙皮法向偏差可以看出,利用夹具主动进行法向定位补偿可以有效减小壁板件的装配偏差,改善装配质量,验证了本模型的正确性和有效性。

表5 补偿前后的飞机壁板件法向偏差对比Table 5 Normal variation of aircraft fuselage panel before and after compensation
夹具定位补偿优化方法作为前瞻性的基础研究,对现有的装配变形偏差分析方法是一种有力的补充。本案例借鉴了某飞机制造厂现有的工艺装备,其定位补偿方法尚未应用于实际装配生产中。从铝板实验数据和壁板件仿真结果来看,本文的方法对于改善飞机壁板装配质量,提高外形准确度是具有可行性的。
4 结 论
1) 基于夹具定位对柔性装配尺寸的作用机理,结合柔性件装配过程,引入夹具法向补偿量,建立了基于夹具主动定位补偿的柔性件装配偏差模型。
2) 根据装配偏差模型特点,提出了夹具补偿量的优化模型和求解方法,建立了基于夹具法向定位补偿的柔性件装配偏差优化方法。
3) 通过金属薄板装配和飞机壁板件装配两个实例,分别利用实验及有限元仿真,验证了夹具主动定位补偿对于优化装配质量的有效性和准确性。本文的研究为飞机装配尺寸质量控制提供了新的思路和高效可靠的技术途径。
[1] TAKEZAWA N. An improved method for establishing the process wise quality standard[R]. Tokyo: Union of Japanese Scientists and Engineers, 1980.
[2] LIU C, HU S J. An offset finite element model and its applications in predicting sheet metal assembly variation[J]. International Journal of Machine Tools & Manufacture, 1995, 35(11): 1545-1557.
[3] LIU S C, HU S J, WOO T C. Tolerance analysis for sheet metal assembly[J]. Transactions of the ASME, 1996, 118(1): 62-67.
[4] LIU C, HU S J. Variation simulation for deformable sheet metal assemblies using finite element methods[J]. Journal of Manufacturing Science & Engineering, 1997, 119(3): 368-374.
[5] CAI W, HU S J, YUAN J X. Deformable sheet metal fixturing: principles, algorithms, and simulations[J]. Journal of Manufacturing Science and Engineering, 1996, 118(3): 318-324.
[6] HU S J, KOREN Y. Stream of variation theory for automotive body assembly[J]. CIRP Annals-Manufacturing Technology, 1997, 46(1): 1-6.
[7] HSIEH C C, KONG P O. A framework for modeling variation in vehicle assembly processes[J]. International Journal of Vehicle Design, 1997, 18(5): 466-473.
[8] HSIEH C C, KONG P O. Simulation and optimization of assembly processes involving flexible parts[J]. Journal of Manufacturing Science & Engineering, 1997, 18(5): 455-465.
[9] EIMARAGHY H A. Geometric design tolerancing: Theories, standards and applications[M]. Berlin: Springer, 1998: 208-219.
[10] CAMELIO J, HU S J, CEGLAREK D. Modeling variation propagation of multi-station assembly systems with compliant parts[J]. Journal of Mechanical Design, 2003, 125(125): 673-681.
[11] CAMELIO J A, HU S J, CEGLAREK D. Impact of fixture design on sheet metal assembly variation[J]. Journal of Manufacturing Systems, 2002, 23(23): 182-193.
[12] 田兆青, 来新民, 林忠钦. 多工位薄板装配偏差流传递的状态空间模型[J]. 机械工程学报, 2007, 43(2): 202-209.
TIAN Z Q, LAI X M, LIN Z Q. State space model of variations stream propagation in multi-station assembly process of sheet metal[J]. Journal of Mechanical Engineering, 2007, 43(2):202-209 (in Chinese).
[13] CUI A, ZHANG H P. Tolerance allocation and maintenance optimal design for fixture in multi-station panel assembly process[J]. Applied Mechanics & Materials, 2010, 34-35:1039-1045.
[14] 邢彦锋, 赵晓昱, 吴伟蔚. 基于夹具配置的薄板件装配偏差分析模型[J]. 计算机集成制造系统, 2010, 16(2): 280-286.
XING Y F, ZHAO X Y, WU W W. Assembly variation analysis model based on fixture configurations for sheet metal parts[J]. Computer Integrated Manufacturing Systems, 2010,16(2): 280-286 (in Chinese).
[15] DAHLSTRÖM S, LINDKVIST L. Variation simulation of sheet metal assemblies using the method of influence coefficients with contact modeling[J]. Journal of Manufacturing Science and Engineering, 2007, 129(3): 615-622.
[16] 谭昌柏, 袁军, 周来水. 基于宽容分层序列法的飞机装配公差稳健设计技术[J]. 中国机械工程, 2012, 23(24): 2962-2967.
TAN C B, YUAN J, ZHOU L S. Robust tolerancing for aircraft assembly based on tolerant lexicographic method[J]. China Mechanical Engineering, 2012, 23(24): 2962-2967 (in Chinese).
[17] 陈晖, 谭昌柏, 王志国. 耦合几何与材料误差的柔性装配偏差统计分析[J]. 航空学报, 2015, 36(9): 3176-3186.
CHEN H, TAN C B, WANG Z G. Statistical variation analysis of compliant assembly coupling geometrical and material error[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(9): 3176-3186 (in Chinese).
[18] 于奎刚, 金隼, 来新民. 基于Taguchi的柔性薄板装配夹具稳健设计[J]. 上海交通大学学报, 2009, 43(12): 1941-1945.
YU K G, JIN S, LAI X M. A fixture locating robust design method of compliant sheet metal assembly based on Taguchi method[J]. Journal of Shanghai Jiaotong University, 2009, 43(12): 1941-1945 (in Chinese).
[19] CAI N, QIAO L. Rigid-compliant hybrid variation modeling of sheet metal assembly with 3D generic free surface[J]. Journal of Manufacturing Systems, 2016(41): 45-64.
[20] 孙辉鹏, 谭昌柏, 安鲁陵, 等. 基于并联装配模型的飞机壁板件装配偏差分析[J]. 航空制造技术, 2016(11): 88-102.
SUN H P, TAN C B, AN L L, et al. Assembly variation analysis of aeronautical panels based on the model of assembly in parallel[J]. Aeronautical Manufacturing Technology, 2016(11): 88-102 (in Chinese).
(责任编辑: 李世秋)
Assembly variation optimization method of aircraft compliant parts based on active locating compensation of fixture
ZHANGWei,WANGZhiguo*,TANChangbai,LIUXia
CollegeofMechanicalandElectricalEngineering,NanjingUniversityofAeronauticsandAstronautics,Nanjing210016,China
Compliant parts are widely used in such products as aircrafts and automobiles. It is quite challenging to analyze and control the compliant assembly quality because the assembly is subject to the coupled effect of multiple error sources in part manufacturing, tooling and joining. A new methodology for assembly variation optimization is proposed based on the concept of active fixture locating compensation. First, an assembly variation model is developed by force-deformation analysis in compliant assembly considering fixture normal locating errors. Based on the assembly variation model, an optimization model is further developed to calculate the optimal fixture normal compensation, which takes the locating points of fixture as variables. Case studies on sheet metal assembly and fuselage panel assembly are conducted. Comparative studies are conducted on the two cases, i.e., sheet metal assembly and fuselage panel assembly, in which the assembly variations with and without the proposed active fixture locating compensation are achieved and compared by experiment and Abaqus finite element analysis, respectively. The results show the proposed method can significantly decrease the predictive assembly variations.
compliant assembly; fixture locating; active compensation; assembly variation; optimization
2016-10-18;Revised2016-11-08;Accepted2016-12-08;Publishedonline2016-12-201339
URL:www.cnki.net/kcms/detail/11.1929.V.20161220.1339.002.html
NationalNaturalScienceFoundationofChina(51275236)
2016-10-18;退修日期2016-11-18;录用日期2016-12-08; < class="emphasis_bold">网络出版时间
时间:2016-12-201339
www.cnki.net/kcms/detail/11.1929.V.20161220.1339.002.html
国家自然科学基金 (51275236)
*
.E-mailwzgnuaa@nuaa.edu.cn
张玮, 王志国, 谭昌柏, 等. 基于夹具主动定位补偿的飞机柔性件装配偏差优化方法J. 航空学报,2017,38(6):420862.ZHANGW,WANGZG,TANCB,etal.AssemblyvariationoptimizationmethodofaircraftcompliantpartsbasedonactivelocatingcompensationoffixtureJ.ActaAeronauticaetAstronauticaSinica,2017,38(6):420862.
http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn
10.7527/S1000-6893.2016.420862
V262.4;TH39
A
1000-6893(2017)06-420862-09
*Correspondingauthor.E-mailwzgnuaa@nuaa.edu.cn

