鲁棒成形极化敏感阵列波束的方法及极化估计

虞翔， 李旦， 张建秋

复旦大学 电子工程系， 上海 200433

鲁棒成形极化敏感阵列波束的方法及极化估计

虞翔， 李旦， 张建秋*

复旦大学 电子工程系， 上海 200433

基于极化敏感阵列，提出了一种鲁棒成形阵列波束的方法。该方法首先将阵列的数据模型进行了重新描述，从而获得了信号波达角(DOA)和极化解耦的模型。借助于该模型并对信号的两个极化方向分别进行鲁棒约束，设计出了一个新的鲁棒空域波束空间成形矩阵，利用该矩阵可以获得信号两个极化分量的鲁棒估计。基于特征值分解的方法，最后给出了估计信号极化参数的方法。分析和数值仿真实验均表明：提出的方法，在对DOA估计误差以及阵列位置误差等造成的阵列失配具有较强鲁棒性的同时，也能有效抑制干扰和噪声，进而提升了极化参数估计的性能。

阵列信号处理； 极化估计； 波束成形； 鲁棒性； 凸优化； 特征值分解

极化作为电磁波信号的一个重要特征，在无线通信、雷达等领域具有极大的应用价值[1-7]。在无线通信领域中，利用极化信息可以提升系统的信道容量，还可以提高系统的抗干扰能力以改善通信质量[2-4]。在雷达信号处理中，利用信号的极化可以提高雷达对目标的检测能力、对杂波的抑制能力[5-6]、对目标波达角(Direction of Arrival， DOA)的分辨能力以及估计准确性[2,6-7]。

目前，大多数DOA和极化参数联合估计的方法，主要侧重于对DOA估计方法的改进[8-17]，期待以提高DOA参数的估计性能来改善极化参数的估计性能，而极化参数的估计大多还是沿用文献[12，16]的方法。可是在一些应用场合中，人们更多关注的是极化参数的估计性能。例如，在利用极化参数调制的通信中，往往使用极化来携带信息[3-4]，因此在存在其他干扰以及阵列失配等非理想情况下，尽可能地能够获得准确的极化参数估计，以便后续准确地解码所发送的信息是其关注的问题之一。众所周知，信号的DOA和极化参数是相互耦合于阵列导向矢量之中。为了避免高计算量的四维搜索，通常的措施是先估计DOA参数再估计极化参数[8-17]。由于极化参数的估计依赖于阵列响应矩阵，当DOA估计不准确或者阵列本身存在误差，如阵列位置误差、通道增益误差等时，极化参数的估计精度很难满足应用中的要求。针对这一状况，文献[16]中有提到利用矢量传感器内部存在的旋转不变性来直接估计极化参数的方法。然而该方法需要对估计得到的极化参数和DOA参数进行配对，且为了进一步提高极化参数的估计性能，它仍需要使用估计的DOA来校正极化参数的估计，因此其在本质上其与一般的极化参数估计思路并不存在差异。

本文从空间滤波的角度出发，通过对阵列输出数据的重新描述，获得了解耦DOA和极化参数的数据模型。借助于该模型，提出了以DOA作为参数来成形波束空间的算法，进而获取信号两维极化信息。同时考虑到阵列响应可能存在的失配情况，给出了通过增加约束来提升波束空间滤波器鲁棒性的方法。最后基于特征值分解提出了极化参数估计的方法。分析和仿真实验均表明，本文提出的方法可以有效地提升在非理想条件下极化参数的估计性能。

1 数据模型

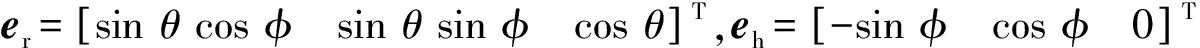
对于完全极化的远场窄带信号，其完整的电磁场信号可以表示为

(1)

式中：V为空域响应矩阵；p为归一化的极化矢量；γ∈[0,π/2)为极化辅助角；η∈[-π,π)为极化相位差异角；s(t)为t时刻基带信号的复包络。完整的电磁场信息共有3个电场分量和3个磁场分量，不同的极化敏感天线，其输出可以通过在式(1)的基础上乘以不同的选择矩阵G，例如：当表示共点正交环偶天线、三偶极子天线以及电磁矢量传感器时，G可以分别用下面的G1、G2和G3表示。

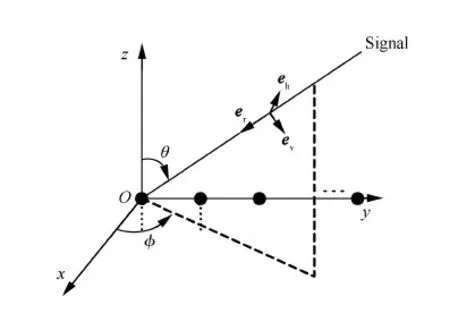
图1 极化敏感天线均匀线阵示意图 Fig.1 Uniform linear array of polarization sensitive antennas

(2)

(3)

G3=I6

(4)

式中：IL为L×L的单位阵，L为任意正整数。

电磁矢量传感器[2]是一种重要的极化敏感天线，它包含了3个正交偶极子和3个正交环形天线。由电磁矢量传感器组成的阵列，它不仅可以像标量阵列那样提取入射电磁波信号在各个传感器上的空间相位信息，还可以完整地感知电磁波信号在各个方向上的投影分量。因此，利用电磁矢量传感器阵列来进行阵列信号处理，如信号参数估计和自适应波束形成等时，它能够获得更好的性能[2,12,15,18]。本文下面的描述与推导中均采用电磁矢量传感器，当使用其他极化敏感天线时，可以将下面获得的结果乘以不同的G即可。

对于图1所示阵列中的第l个电磁矢量传感器，其接收到的信号数据可以表示为

xl(t)=qlVps(t)+nl(t)=qlbps(t)+nl(t)

(5)

(6)

假设期望信号和K-1个干扰信号同时入射到阵列，且期望信号和干扰信号之间互不相关，那么阵列输出数据的完整表达可写成为

(7)

重写阵列的输出数据式(7)为

(8)

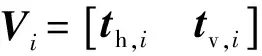
2 空域波束空间算法

传统的极化敏感阵列波束成形算法希望获取期望信号s1(t)，通过对导向矢量a进行约束而得到[18-20]，它需要知道信号的DOA和极化联合的四维参数信息。从式(8)可以看到，其阵列空域响应矩阵T∈C6M×2仅与DOA参数相关，因此可在仅知道信号DOA参数的情况下，通过对矩阵T施加约束而得到一个波束空间成形矩阵WS∈C6M×2，以获取含两维极化信息的信号p1s1(t)，在数学上它可以表示为

(9)

式(9)表明：一旦借助波束空间成形矩阵WS∈C6M×2获得了z(t)，那么就能利用其对极化参数进行估计，进而也可获得期望信号的估计。若期望信号和干扰信号的DOA相同，但其极化方式不同，则可在空域波束空间滤波的基础上，再应用极化域滤波的方法[21-23]将两者分开，因此本文仅考虑目标信号和干扰信号DOA不相同的情况。

空域波束空间滤波后式(9)的能量为

E[zH(t)z(t)]=trace{E[z(t)zH(t)]}=

(10)

式中：trace(·)表示矩阵求迹运算；R为阵列输出数据协方差矩阵。保证期望DOA方向上带两维极化信息的信号无失真通过的约束下，使得式(10)最小化的代价函数可以描述为

(11)

利用拉格朗日数乘法，式(11)的解析解可以写为

(12)

可以看到式(11)与式(12)的形式与传统的Capon算法类似，它们可以看成是矩阵约束版本的Capon算法。但实际上，该目标函数由两个线性最小约束方差(LCMV)波束成形器构成，即

(13)

(14)

3 鲁棒空域波束空间算法

与传统Capon算法类似，当响应矩阵T1存在不确定性时，上述算法性能会严重下降。结合最差性能最优化准则[24]，本节将提出鲁棒的空域波束空间算法。在实际应用中，由于期望DOA或者阵列位置可能存在误差，这样实际的信号水平极化方向矢量th,1和垂直极化方向矢量tv,1就会存在偏差，此时它们可以分别表示为

(15)

h(ε1)

(16)

v(ε1)

(17)

结合最差性能最优化准则，代价函数式(13)和式(14)可以转化为

th,1∈h(ε1)，tv,1∈v(ε1)

(18)

th,1∈h(ε1)，tv,1∈v(ε1)

(19)

可以看到与传统最差性能最优化波束成形器不同的是，代价函数式(18)和式(19)还分别添加了对另一个极化方向的止带约束。考虑到实际极化方向矢量th,1和tv,1本身具有不确定性，因而式(18)和式(19)中的止带等式约束也可以用下面的衰减约束代替：

(20)

式中：ε2为衰减系数，取值应比较小。将式(18)和式(19)中的不等式约束进行转化，得到最终的优化代价函数为

(21)

(22)

4 基于特征值分解的极化参数估计方法

让阵列的快拍经过上面设计得到波束空间滤波矩阵后，理想状态下有

(23)

若直接采用比例关系求解极化参数，由于噪声的影响，极化参数的估计将不是最优的。考虑波束空间输出数据z(t)的协方差矩阵，有

Rz=E[z(t)zH(t)]=R0+WHW

(24)

式中：

(25)

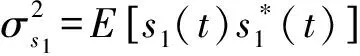
推论空域波束空间矩阵WS满足：

(26)

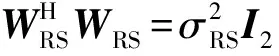
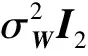
(27)

式中：κ为非零复常数，从而可以得到极化参数γ1和η1的求解公式为

(28)

其中：

(29)

5 数值仿真实验

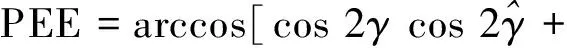
(30)

仿真实验1考察存在阵列失配条件下的极化参数估计性能比较。假设期望信号的DOA先验为(110°,50°)，存在2° 的DOA先验偏差。阵列位置误差满足在区间(-0.2d,0.2d)上的均匀分布。信号与干扰的比率(Signal to Interference Ratio， SIR)固定为-10 dB。文献[12]的方法在低信噪比下收敛概率会下降[12]，在下文的比较中只考虑成功收敛时的性能。文献[16]估计信号子空间时，给出的信号个数先验为2个。本文方法的参数选取ε1=3.5，ε2=10-5。图2为各种方法的极化参数估计性能比较。图2(a)为估计性能与信噪比(Signal to Noise Ratio， SNR)之间的关系，快拍数选用200个。图2(b)为估计性能与快拍数之间的关系，SNR=20 dB。可以看到对于模型存在失配的情况，本文的RSBS算法的极化参数估计误差更小。尤其在信噪比较大的时候，此时模型失配导致误差的因素占据主导，因而RSBS算法的性能优势更加明显。SBS算法需要对信号协方差矩阵进行求逆，因而其对于快拍数量有一定的要求，从图2(b)中可以看到SBS算法在低快拍数下性能较差。

图2 阵列失配条件下，5种算法极化参数估计性能Fig.2 Polarization estimation performance of 5 algorithms with array mismatch

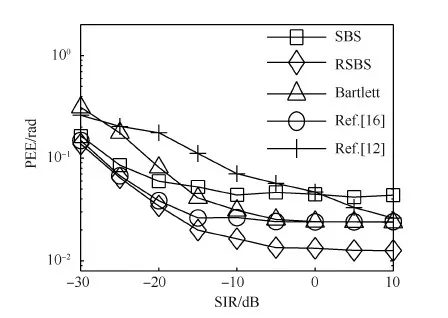
图3 极化参数估计性能与SIR之间的关系Fig.3 Polarization estimation performance vs SIR

仿真实验2考察极化参数估计性能与SIR之间的关系，期望信号和阵列的设置同实验1，干扰信号的功率固定为20 dB。Bartlett为非自适应波束算法，其对于干扰的衰减是固定的，从图3中可以看到Bartlett在低SIR下性能受影响比较严重，而其他算法受此影响比较小。

仿真实验3存在干扰信号不稳定情况时的极化参数估计性能比较。整个观察区间共有200个快拍，信号以及阵列的设置同实验1。干扰信号存在突然出现、突然消失的情况：干扰信号1的设置同上；干扰信号2的DOA参数为(40°,50°)，极化参数为(50°,-45°)，其出现的区间为[1,60]∪[150,200]；干扰信号3的DOA参数为(130°,170°)，极化参数为(50°,60°)，其出现区间为[100,200]。信号和各个干扰信号之间的SIR均为-10 dB。文献[12，16]的方法要求在观察区间内信号子空间是稳定的，因而在实验3条件下两种方法均失效。图4比较了SBS、RSBS和Bartlett算法的极化参数估计的性能。空间滤波的算法不会受到干扰信号不稳定的情况影响，对比图2(a)，可以看到性能基本不受影响。

图4 干扰信号不稳定情况下，3种算法的极化估计性能 Fig.4 Polarization estimation performance of 3 algorithms with unstable interferences

6 结 论

1) 常用的极化参数估计方法依赖于信号子空间的估计或者信号导向矢量的估计，因而其估计性能会受到信号子空间或者信号导向矢量估计准确性的影响，并且这些极化参数估计算法的使用环境也会受到限制，鲁棒性较差。

2) 本文从空域滤波的角度出发，通过设计一个鲁棒的波束空间滤波器，来得到期望信号的两维极化分量以用于后续的极化参数估计，提升了存在DOA先验误差和阵列位置误差等这些可能导致阵列失配情况下的极化参数估计性能，同时其应用领域也得以扩展，适用于在整个观察区间内干扰信号突然消失或者突然出现的情况。

[1] KOSTINSKI A B, BOERNER W M. On foundations of radar polarimetry [J]. IEEE Transactions on Antennas and Propagation, 1986, 34(12): 1395-1404.

[2] NEHORAI A, PALDI E. Vector-sensor array processing for electronmagnetic source localization[J]. IEEE Transactions on Signal Processing, 1994, 42(2): 376-398.

[3] 宋汉斌. 三维调制和解调 [D]. 上海： 复旦大学, 2012.

SONG H B. Three-dimensional modulator and demodulator[D]. Shanghai: Fudan University, 2012 (in Chinese).

[4] 吴昊. 四维无线调制解调器的理论研究 [D]. 上海： 复旦大学, 2014.

WU H. Theoretical research on four-dimensional wireless modulator and demodulator[D]. Shanghai: Fudan University, 2014 (in Chinese).

[5] CHAMBERLAIN N E, WALTON E K, GARBER F D. Radar target identification of aircraft using polarization-diverse features[J]. IEEE Transactions on Aerospace and Electronic Systems, 1991, 27(1): 58-67.

[6] 徐振海. 极化敏感阵列信号处理的研究[D]. 长沙： 国防科学技术大学, 2004.

XU Z H. Signal processing based on polarization sensitive array[D]. Changsha: National University of Defense Technology, 2004 (in Chinese).

[7] SCHMIDT R. A signal subspace approach to multiple emitter location and spectral estimation[D]. San Francisco, CA: Stanford University, 1981.

[8] LI J, STOICA P, ZHENG D M. Efficient direction and polarization estimation with a COLD array[J]. IEEE Transactions on Antennas and Propagation, 1996, 44(4): 539-547.

[9] WONG K T. Direction finding/polarization estimation-dipole and/or loop triad(s)[J]. IEEE Transactions on Aerospace and Electronic Systems, 2001, 37(2): 679-684.

[10] WONG K T, YUAN X. “Vector cross-product direction-finding” with an electromagnetic vector-sensor of six orthogonally oriented but spatially noncollocating dipoles/loops[J]. IEEE Transactions on Signal Processing, 2011, 59(1): 160-171.

[11] WONG K T, ZOLTOWSKI M D. Closed-form direction finding and polarization estimation with arbitrarily spaced electromagnetic vector-sensors at unknown locations[J]. IEEE Transactions on Antennas and Propagation, 2000, 48(5): 671-681.

[12] WONG K T, ZOLTOWSKI M D. Self-initiating MUSIC-based direction finding and polarization estimation in spatio-polarizational beamspace[J]. IEEE Transactions on Antennas and Propagation, 2000, 48(8): 1235-1245.

[13] 刘兆霆, 刘中, 何劲. 线性极化敏感阵列的极化平滑算法及相干源参数估计 [J]. 航空学报, 2010, 31(8): 1646-1652.

LIU Z T, LIU Z, HE J. Polarization smoothing-based direction finding and polarization estimation of coherent sources with linear electromagnetic vector sensor array[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(8): 1646-1652 (in Chinese).

[14] LIU J, LIU Z, LIU Q. Direction and polarization estimation for coherent sources using vector sensors[J]. Journal of Systems Engineering and Electronics, 2013, 24(4): 600-605.

[15] 徐有根， 刘志文. 电磁矢量传感器阵列相干信号源波达方向和极化参数的同时估计： 空间平滑法 [J]. 通信学报, 2004, 25(5): 28-38.

XU Y G, LIU Z W. Simultaneous estimation of 2-D DOA and polarization of multiple coherent sources using an electromagnetic vector sensor array[J]. Journal of China Institute of Communications, 2004, 25(5): 28-38 (in Chinese).

[16] LI J. Direction and polarization estimation using arrays with small loops and short dipoles[J]. IEEE Transactions on Antennas and Propagation, 1993, 41(3): 379-387.

[17] YUAN Q W, CHEN Q, SAWAYA K. MUSIC based DOA finding and polarization estimation using USV with polarization sensitive array antenna[C]//IEEE Radio and Wireless Symposium, 2006: 339-342.

[18] NEHORAI A, HO K C, TAN B T G. Minimum-noise-variance beamformer with an electromagnetic vector sensor[J]. IEEE Transactions on Signal Processing, 1999, 47(3): 601-618.

[19] AHMAD M I, LIU Z W, XU Y G. Minimum variance beamforming using polarization sensitive array[C]//IEEE Singapore International Conference on Communication System. Piscataway, NJ: IEEE Press, 2008: 489-492.

[20] TAO J W, CHANG W X. A novel combined beamformer based on hypercomplex processes[J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(2): 1276-1289.

[21] XUE J H, ZHOU H J, QIAO X L. Adaptive filtering in polarization domain with the criterion of LCMV[C]//CIE International Conference on Radar, 2006: 1-4.

[22] CAO B, ZHANG Q Y, LIANG D, et al. Blind adaptive polarization filtering based on oblique projection[C]//IEEE International Conference on Communications. Piscataway, NJ: IEEE Press, 2010: 1-5.

[23] LIU J, ZHANG Z J. A new polarization filter based on weighted combination[C]//IEEE International Conference on Signal Processing. Piscataway, NJ: IEEE Press, 2010: 2168-2171.

[24] VOROBYOV S A, GERSHMAN A B, LUO Z Q. Robust adaptive beamforming using worst-case performance optimization: A solution to the signal mismatch problem[J]. IEEE Transactions on Signal Processing, 2003, 51 (2): 2257-2269.

[25] LI J, COMPTON R T. Angle and polarization estimation using ESPRIT with a polarization sensitive array[J]. IEEE Transactions on Antennas and Propagation, 1991, 39(9): 1376-1383.

[26] HARRY L V T. Optimum array processing: Part IV of detection, estimation, and modulation theory[M]. New York: Wiley-InterScience, 2002: 37-59.

(责任编辑： 苏磊)

附录A

假设干扰信号只有一个，当存在多个干扰信号时，可在下述的推导基础上类推得到。此时阵列输出数据为

x(t)=a1s1(t)+a2s2(t)+n(t)

(A1)

其协方差矩阵为

对于阵列导向矢量a和阵列空域响应矩阵T，存在aHa=2M，THT=2MI2的关系。因而应用矩阵求逆公式可以得到输出数据协方差矩阵的逆矩阵：

(A2)

(A3)

(A4)

(A5)

忽略高次项可得到R-1的近似值为

(A6)

(A7)

A robust beamformer with a polarization sensitive array andpolarization estimation

YUXiang,LIDan,ZHANGJianqiu*

DepartmentofElectronicEngineering,FudanUniversity,Shanghai200433,China

Based on the polarization sensitive array, a robust beamformer for polarization estimation is proposed. By reformulating the model for polarization sensitive array data, a model decoupling the direction of arrival (DOA) parameters from the polarization ones is given. Based on our model and the robust constraints to the two polarization directions of a signal, a spatial beamspace matrix is designed to robustly obtain an estimation of the signal’s two polarization components. The polarization parameter estimations of the signal are then given by the eigenvalue decomposition. Both analyses and simulation results show that our beamformer is robust to the array mismatch caused by the DOA estimate and array position errors. It is also indicated that our method can improve the performance of the polarization estimation effectively by suppressing the interference and noise are suppressed.

array signal processing; polarization estimation; beamforming; robustness; convex optimization; eigenvalue decomposition

2016-09-05；Revised2016-11-04；Accepted2016-11-24；Publishedonline2016-12-081610

URL：www.cnki.net/kcms/detail/11.1929.V.20161208.1610.002.html

NationalNaturalScienceFoundationofChina(61571131)

2016-09-05；退修日期2016-11-04；录用日期2016-11-24； < class="emphasis_bold">网络出版时间

时间：2016-12-081610

www.cnki.net/kcms/detail/11.1929.V.20161208.1610.002.html

国家自然科学基金 (61571131)

*

.E-mailjqzhang@fudan.ac.cn

虞翔， 李旦， 张建秋． 鲁棒成形极化敏感阵列波束的方法及极化估计J． 航空学报,2017,38(6):320752.YUX,LID,ZHANGJQ.ArobustbeamformerwithapolarizationsensitivearrayandpolarizationestimationJ.ActaAeronauticaetAstronauticaSinica,2017,38(6):320752.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2016.0312

V243.4; TN911.7

A

1000-6893(2017)06-320752-08

*Correspondingauthor.E-mailjqzhang@fudan.ac.cn