平台摇摆对卡尔曼滤波跟踪精度的影响
程晗, 陈维义, 谢芝亮
海军工程大学 兵器工程系, 武汉 430033
平台摇摆对卡尔曼滤波跟踪精度的影响
程晗*, 陈维义, 谢芝亮
海军工程大学 兵器工程系, 武汉 430033
通过建立目标相对运动坐标系和目标相对运动观测模型,研究了在平台摇摆影响下,跟踪系统观测到的目标运动状态的变化。在分析捷联垂直基准补偿原理的基础上建立了捷联垂直基准平台摇摆角补偿模型,建立的模型结合捷联垂直基准系统的测量能力对其补偿算法进行了理论推导,使模型适用于实际捷联垂直基准系统。通过建立模型以及仿真研究了平台摇摆作用下卡尔曼滤波跟踪精度的变化,指出了摆造成卡尔曼滤波跟踪精度降低甚至离散的主要原因在于模型误差增大。设计仿真实验验证了结论的正确性,为进一步改进跟踪手段提供了理论参考。
平台摇摆; 相对运动观测模型; 捷联垂直基准; 卡尔曼滤波跟踪; 模型误差
卡尔曼滤波算法由于其递推形式易应用于计算机,已被广泛运用于航空航天和军事领域。文献[1]指出,卡尔曼滤波算法在运用于目标跟踪过程中存在对数学模型依赖性较大的特点。与此同时,运动平台(如航空飞行器、水面舰艇等)在工作时,由于受到风、波浪、潮汐等自然环境因素的作用,会产生周期性的摇摆和震荡,从而造成其平台上全部仪器和设备的摇摆运动[2-3]。在平台摇摆运动的影响下,目标相对跟踪系统的观测运动状态会产生较大的随机性和不可预测性,从而给滤波跟踪带来较大的困难[4-5]。本文通过建立相对运动观测模型,研究了平台摇摆下跟踪系统所观测目标运动状态的变化,对捷联垂直基准补偿原理进行了研究,结合卡尔曼滤波跟踪算法的相关理论基础,通过建立模型分析了平台摇摆对卡尔曼滤波跟踪精度的影响。所得到的结论为进一步研究运动平台跟踪系统、改进跟踪手段提供了理论参考。
1 目标相对跟踪系统运动模型
运动平台受环境因素影响在空间的运动主要包括横摇、纵摇、艏摇、横荡、纵荡、垂荡等,其中垂荡、纵荡和横荡运动属于平动,可以通过研究目标相对平台摇摆中心的平动进行简化,对于平台的横摇、纵摇和艏摇,则需要建立合适的坐标系进行研究[6]。
1.1 坐标系选取
研究目标的相对运动,需要选取合适的坐标系。在实际应用中,习惯于对平台的姿态做出如下规定:① 对于平台的横摇,取向右舷倾斜为正;② 对于平台的纵摇,取艏部向上倾斜为正。为了便于计算,使平台摇摆运动方向和坐标轴的方向满足右手螺旋定则,建立如下3种坐标系:
1) 平动坐标系O-XYZ
平动坐标系原点O位于跟踪平台的摇摆中心,X轴与平台运动方向在水平面内的投影重合,Y轴垂直于X轴落于水平面内,取落于跟踪平台右舷方向为正,Z轴垂直于水平面向上。该坐标系内的位置坐标用[xyz]表示。
2) 观测平面坐标系O-XbYbZb
观测平面坐标系原点与平动坐标系原点重合,Xb轴在观测平面内指向舷艏,Yb轴垂直于Xb轴落于观测平面内,取落于观测平面右舷方向为正,Z轴垂直于观测平面向上。该坐标系内坐标用[xbybzb]表示。
3) 跟踪测量坐标系Or-XrYrZr
跟踪测量坐标系由观测平面坐标系平动获得,其坐标原点落于跟踪系统的探测中心。该坐标系内坐标用[xryrzr]表示。
对于典型的三坐标雷达,其直接测量的参数为目标相对其距离、俯仰角和偏角(包括其随时间的变化量),经过变换后可获得目标在跟踪测量坐标系内的具体参数。本文主要研究卡尔曼滤波跟踪过程,暂不将此球坐标到直角坐标的变换过程纳入研究范围内。
1.2 坐标变换与相对运动观测模型
(1)

(2)
式(2)为平动坐标系到跟踪测量坐标系的位置坐标变换公式。通常的坐标变换过程一般只能表征空间位置坐标的变换过程,但是实际情况中,目标处于运动状态,我方跟踪系统还需要对目标的速度甚至加速度进行测量,因此在建立目标相对运动模型时,还需要推导目标运动速度的变换矩阵。
令式(2)两边对时间求偏导:
(3)
式中:vrx、vry和vrz分别为目标在跟踪测量坐标系内3个方向的运动速度;vx、vy和vz分别为目标在平动坐标系内3个方向的运动速度。dB/dt通过对位置坐标变换矩阵内各元素对时间求偏导获得,其中平台摇摆角度对时间的偏导dξj/dt、dηj/dt和dζj/dt可由ωjξ、ωjη和ωjζ替代,其物理意义为平台横摇、纵摇和艏摇的角速度。
式(3)为平动坐标系到跟踪测量坐标系的速度变换公式,要求取加速度变换公式则另两边再对时间求偏导即可,在此不作赘述。
根据上述推导过程可以发现,跟踪系统观测到的目标运动状态主要受到三方面的影响:① 目标在惯性空间的实际运动状态;② 平台摇摆运动状态;③ 观测设备的安装位置误差。
2 捷联垂直基准及其补偿模型
在平台摇摆的作用下,原本运动状态简单、规律的目标其相对跟踪系统的运动状态也会变得复杂而无规律可循,假设某目标自跟踪平台匀速直线远离,则其相对跟踪平台运动的实际轨迹与跟踪系统的观测轨迹如图1所示。

图1 平台摇摆作用下目标轨迹和观测轨迹Fig.1 Target trajectory and observed trajectory under influence of platform swaying
由文献[7]可知,观测轨迹的复杂化、无规律化会对目标跟踪精度产生较大影响,结合文献[8-16]中关于卡尔曼滤波跟踪特性的研究可知,目标运动状态的变化情况对卡尔曼滤波跟踪效果会产生较大的影响,严重时甚至会产生跟踪轨迹的离散,使得跟踪过程失效。因此需要借助捷联垂直基准对平台的摇摆运动进行补偿。
2.1 捷联垂直基准补偿原理
捷联垂直基准可以实时获取其安装平台的横摇和纵摇运动参数,同时,通过罗经可以获取运动平台的艏摇参数,因此在进行补偿运算时,可以一并对观测信号进行补偿[17-20]。
(4)
结合式(4)可知,在已知跟踪系统的观测信号和捷联垂直基准测得的平台摇摆运动信号的情况下,可以获得目标相对观测平台的实际位置跟踪信号。同时由式(3)可知,令式(4)两端对时间分别求偏导,即可获得目标相对观测平台的实际速度跟踪信号。
通过上述方法,即可将观测到的目标运动转换为目标相对观测平台的实际运动,实现对平台摇摆运动的补偿。
2.2 目标运动状态跟踪补偿模型
假设某时刻通过惯性系统测量的平台摇摆角测量信息为[ξbηbζb],平台摇摆角速度测量信息为[ωbξωbηωbζ]。定义此刻的相对位置补偿矩阵为

(5)
假设某时刻跟踪系统对目标的观测信号为Sg=[PgVg],其中Pg=[xgygzg]T为位置观测信息,Vg=[vgxvgyvgz]T为速度观测信息。则可以算得补偿后目标相对平台的位置跟踪信息为
(6)
令式(6)两边对时间求偏导,可以算得补偿后目标相对平台的速度跟踪信息为
(7)
式中:dA/dt由矩阵A内各元素对时间求偏导所得;其中dξb/dt、dηb/dt和dζb/dt分别由ωbξ、ωbη和ωbζ代替进行计算。
3 跟踪精度影响分析
根据大量文献对卡尔曼滤波算法的实验研究和仿真验证结果可知,卡尔曼滤波算法对目标运动的数学模型存在较大的依赖性,在跟踪目标参数变化规律无法被滤波算法递推函数所描述时,算法的跟踪精度会明显下降。由图1可知,在平台摇摆运动的作用下,跟踪系统的观测轨迹会变得难以被确定的递推函数所描述。
3.1 卡尔曼滤波算法基本假设
对于一般用于目标跟踪的卡尔曼滤波算法,需要根据目标运动规律和跟踪系统的跟踪能力进行基本假设。

X(k+1)=Φ(k)X(k)+w(k)
(8)
式中:Φ(k)为k时刻的目标运动状态转移矩阵;w(k)为该时刻目标运动状态噪声。由于一般目标运动状态存在未知性,因此通常采用常加速度模型,即对Φ(k)作出如下假设:
(9)
式中:Δ为跟踪系统观测时间间隔(采样周期)。
假设k时刻跟踪系统观测到的目标运动状态为Y(k),其与目标实际状态X(k)之间存在如下关系:
Y(k)=Θ(k)X(k)+v(k)
(10)


(11)
根据以上滤波算法的基本假设可知,基于该假设的滤波算法对常加速运动的目标跟踪效果最好,然而由之前的研究可知,在平台摇摆运动的影响下,跟踪系统观测到的目标运动几乎不可能是匀加速运动,因此一定会产生较大的偏差,这就需要利用捷联垂直基准的数据对观测数据进行补偿。
3.2 平台摇摆对卡尔曼滤波影响分析
根据假设,在平台摇摆的影响下,采用卡尔曼滤波算法直接对跟踪设备的初始观测信号进行滤波跟踪会产生较大的偏离,要达到理想的跟踪效果,需要先对初始观测信号进行补偿,接下来再对补偿后的跟踪信号进行滤波跟踪处理,才能有效地发挥卡尔曼滤波跟踪的优势。为了验证上述假设是否合理,设计仿真实验就台摇摆对卡尔曼滤波跟踪效果的影响进行分析。
1) 目标实际运动状态满足滤波算法基本假设
假设目标相对观测平台的实际运动状态为匀速直线运动,由平台摇摆中心开始远离,记录下对原始观测信号进行补偿后的卡尔曼滤波跟踪轨迹;同时记录直接采用卡尔曼滤波跟踪的目标状态数据,利用跟踪平台的摇摆参数对该数据进行坐标变换处理,得到平动坐标系下的跟踪变换轨迹,目标的相对运动轨迹和两组跟踪轨迹图如图2所示。

图2 直线运动目标跟踪轨迹Fig.2 Tracking trajectory of rectilinear target
由图中跟踪轨迹可以明显地发现,对于运动状态满足滤波跟踪基本假设的目标,若先进行补偿后进行滤波跟踪,跟踪轨迹几乎与目标轨迹相重合;而直接采用卡尔曼滤波跟踪获得的跟踪信号出现了较大的偏差,跟踪失效。实验结果满足之前的假设。
2) 目标实际运动状态不满足算法的基本假设
假设目标围绕平台所在铅垂线做圆周运动,分别采用两种方式进行跟踪的轨迹如图3所示。

图3 圆周运动目标跟踪轨迹Fig.3 Tracking trajectory of circular motional target
由图中轨迹可以看出,当运动状态不满足跟踪基本假设时,两种跟踪都会产生明显的跟踪偏离,此时需针对卡尔曼滤波算法本身进行修正以弥补模型误差。
由上述仿真实验中的结果可以发现,在平台摇摆运动的影响下,卡尔曼滤波的跟踪效果明显降低,这是由于在摇摆运动的作用下,跟踪系统观测到的目标运动状态表现出较大的无规律性,而滤波算法采用的数学模型无法满足跟踪需求,从而导致滤波估计值产生较大误差,进一步造成滤波跟踪的失效。与此同时,采用垂直捷联基准对跟踪系统的观测数据进行补偿之后,再采用卡尔曼滤波跟踪能有效弥补平台摇摆对滤波算法带来的影响,从而有效地提高了跟踪精度。
4 仿真验证
上述研究过程利用仿真模型定性地研究了平台摇摆对卡尔曼滤波跟踪效果的影响,而针对卡尔曼滤波相关领域的许多研究成果也能有效地补偿标准卡尔曼滤波跟踪的模型误差,达到避免跟踪失效的目的,其中文献[1]提出的修正卡尔曼滤波算法就能实现这一目的,为了进一步证明本文研究结论的正确性和实用意义,下面设计仿真实验针对修正卡尔曼滤波跟踪进行定量分析验证。
假设平台摇摆运动均为周期运动,其随时间的变化模拟为
(12)
式中:ξmax、ηmax和ζmax分别为横摇、纵摇和艏摇的最大角;Tξ、Tη和Tζ分别为横摇、纵摇和艏摇周期。
假设捷联垂直基准能够实时测量平台摇摆的角度和角速度信息,其测量信息为
(13)
式中:[ξbηbζb]为平台摇摆角度的测量信息;[ωbξωbηωbζ]为平台摇摆角速度的测量信息;[ωjξωjηωjζ]和[JjξJjηJjζ]分别为平台摇摆的实际角速度和角加速度信息;r为捷联垂直基准在该时刻的测量噪声。
采用100次蒙特卡罗法对跟踪过程中空间位置的均方根误差R进行统计计算,其定义为

(14)

(15)
式中:d为某时刻跟踪估计位置与目标实际位置之间的空间距离;N为运行仿真的次数。
4.1 平台摇摆程度对卡尔曼滤波跟踪效果影响
根据不同的平台航行环境,分3种模式模拟平台的摇摆状态,如表1所示。

表1 模拟平台摇摆状态参数Table 1 Simulation parameters of swaying status
1) 采用修正卡尔曼滤波对匀加速运动目标跟踪
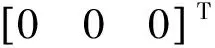
其中轻度模式下,位置均方根误差最大值为5.722 m,平均值为5.068 5 m;中度模式下,位置均方根误差最大值为8.13 m,平均值为5.958 1 m;重度模式下,位置均方根误差最大值为17.06 m,平均值为8.068 1 m。对比3组数据可以发现,随着平台摇摆程度的加深,采用修正卡尔曼滤波的跟踪精度逐渐降低,这与前面的假设相吻合。
2) 采用修正卡尔曼滤波对圆周运动目标跟踪
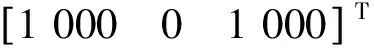
其中轻度模式下,位置均方根误差最大值为6.247 m,平均值为5.279 9 m;中度模式下,位置均方根误差最大值为8.252 m,平均值为6.433 0 m;重度模式下,位置均方根误差最大值为9.653 m,平均值为7.363 5 m。对比上述3组数据和前面对匀加速运动目标跟踪的位置均方根误差,发现在平台摇摆运动的影响下,目标的运动状态对修正卡尔曼滤波跟踪的影响并不明显。

图4 各摇摆模式下对匀加速运动和圆周运动目标跟踪位置的均方根误差Fig.4 Position RMS tracking error of uniformly accelerated and circular motional targets under different swaying modes
4.2 捷联垂直基准系统精度对卡尔曼滤波跟踪效果影响
上述的实验验证了前面关于平台摇摆状态对卡尔曼滤波跟踪影响的假设,为了进一步分析其内在原因,下面引入捷联垂直基准系统对跟踪系统观测数据进行补偿,研究捷联垂直基准系统精度对卡尔曼滤波跟踪效果的影响。为了突出补偿效果,下面仿真实验中平台摇摆程度统一设定为重度模式。
假设捷联垂直基准系统的测量噪声分别满足:
(16)
1) 匀加速直线运动目标跟踪
假设目标自平台的摇摆中心远离,其运动状态与之前的实验假设相一致,跟踪系统的参数保持不变。图5为不同的捷联垂直基准系统精度条件下采用修正卡尔曼滤波跟踪算法的位置均方根误差变化。
其中,捷联垂直基准系统精度水平取r1时,其位置均方根误差最大值为17.27 m,平均值为9.029 4 m;取r2时,其位置均方根误差最大值为11.35 m,平均值为5.234 9 m;取r3时,其位置均方根误差最大值为10.9 m,平均值为5.15 m;直接采用修正卡尔曼滤波跟踪,其位置均方根误差最大值为17.12 m,平均值为8.078 4 m。对比上述4组数据发现,当捷联垂直基准系统精度水平取r1时,其前半部跟踪精度轨迹要明显优于不采取补偿的跟踪轨迹,而在后半部分轨迹上升明显;当捷联垂直基准系统精度水平取r2和r3时,其整体轨迹都要优于不采取补偿的跟踪轨迹,但是尽管两者精度水平差了两个数量级,但是相互之间差距并不是特别明显。
2) 圆周运动目标跟踪
假设目标围绕平台所在铅垂线做圆周运动。
其中,捷联垂直基准系统精度水平取r1时,其位置均方根误差最大值为7.672 m,平均值为6.316 9 m;取r2时,其位置均方根误差最大值为7.492 m,平均值为6.200 8 m;取r3时,其位置均方根误差最大值为7.965 m,平均值为6.172 1 m;直接采用修正卡尔曼滤波跟踪,其位置均方根误差最大值为10.81 m,平均值为7.442 6 m。对比上述4组数据发现,当滤波算法假设不满足目标的实际运动状态时,采用捷联垂直基准系统进行补偿的效果比不上对匀加速目标进行跟踪时的明显,而且各个精度水平下其误差水平相差并不远;对比各补偿精度下不同目标运动状态的误差数据可发现,除却精度水平为r1时,采取捷联垂直基准系统补偿的情况下针对匀加速目标的跟踪效果要明显优于针对圆周运动目标的跟踪效果,这从侧面验证了前面关于平台摇摆对卡尔曼滤波跟踪影响的假设。
通过对比上述两组仿真实验中的实验数据以及位置均方根误差随时间变化图可知:
1) 平台摇摆程度的加重会大幅增大卡尔曼滤波跟踪的模型误差,造成跟踪精度下降,与此同时,滤波算法假设不满足跟踪目标的实际运动状态也是模型误差的主要来源。

图5 各补偿精度下对匀加速运动和圆周运动目标跟踪位置的均方根误差 Fig.5 Position RMS tracking error of uniformly accelerated and circular motional targets under different compensation precisions
2) 当滤波算法满足目标运动状态时,采用满足一定精度条件的捷联垂直基准系统对观测信号进行补偿,能有效降低滤波算法的模型误差,但在满足精度条件时,进一步提高捷联垂直基准系统的精度对提高卡尔曼滤波跟踪精度的效果并不明显,这是由于采用捷联垂直基准系统只能补偿滤波算法的模型误差,而其本身的精度水平并不是影响卡尔曼滤波跟踪精度的决定性因素。
3) 采用捷联垂直基准系统对平台摇摆进行补偿时需要结合目标距离满足一定的精度水平,否则其自身误差会随目标距离观测中心的距离增大,导致跟踪效果降低。
4) 对卡尔曼滤波跟踪算法进行合理改进能有效提高跟踪精度和避免出现跟踪失效的现象,然而其根本问题在于目标运动状态模型无法满足实际运动状态,因此对于卡尔曼滤波算法的研究仍有很大的空间。
5 结 论
1) 对捷联垂直基准参数对平台摇摆的补偿原理进行了分析,对捷联垂直基准补偿变换算法进行了理论推导。
2) 分析了平台摇摆对卡尔曼滤波跟踪精度的影响,指出模型误差增大是主要原因。
[1] 杨永健, 樊晓光, 王晟达, 等. 基于修正卡尔曼滤波的目标跟踪[J]. 系统工程与电子技术, 2014, 36(5): 846-851.
YANG Y J, FAN X G, WANG S D, et al. Target tracking based on amendatory Kalman filter[J]. System Engineering and Electronics, 2014, 36(5): 846-851(in Chinese).
[2] 余戌瞳, 吴玲, 卢发兴. 舰艇摇摆下射界动态变化对武器目标分配的影响[J]. 兵工学报, 2015, 36(9): 1819-1824.
YU X T, WU L, LU F X. The influence of dynamically changing firing zone on weapon-target assignment under ship swaying[J]. Acta Armamentarii, 2015, 36(9): 1819-1824 (in Chinese).
[3] 刘玉洲. 舰艇摇摆对雷达侧向精度及工作方式的影响[J]. 舰船电子对抗, 2002, 25(2): 18-21.
LIU Y Z. The influence on working mode of radar direction accuracy from ship swaying[J]. Shipboard Electronic Countermeasure, 2002, 25(2): 18-21 (in Chinese).
[4] 窦林涛, 初阳, 程建庆. 舰载雷达系统误差建模仿真分析[J]. 系统仿真学报, 2013, 25(4): 188-192.
DOU L T, CHU Y, CHENG J Q. Modeling and simulation analysis of error from shipboard radar[J]. Journal of System Simulation, 2013, 25(4): 188-192 (in Chinese).
[5] 孙世岩, 张国栋. 舰艇摇摆对雷达目标跟踪精度的影响分析[J]. 火力指挥控制, 2011, 36(5): 75-78.
SUN S Y, ZHANG G D. Target tracking error analysis caused by ship’s pitch and roll[J]. Fire Control & Command Control, 2011, 36(5): 75-78 (in Chinese).
[6] 朱绍强, 李相民, 李丹. 舰炮武器系统海上动态精度实验可行性探讨[J]. 舰船电子工程, 2012, 32(3): 94-96.
ZHU S Q, LI X M, LI D. Feasibility discussion of dynamic accuracy test at sea for navy gun weapon system[J]. Ship Electronic Engineering, 2012, 32(3): 94-96 (in Chinese).
[7] 付强, 朱纪洪, 王春平. 蛇形机动目标航迹旋转对射弹脱靶量的影响[J]. 清华大学学报(自然科学版), 2015, 55(8): 884-888.
FU Q, ZHU J H, WANG C P. Impact of space rotation on shell distances for serpentine fight path maneuvering[J]. Journal of Tsinghua University (Science and Technology), 2015, 55(8): 884-888 (in Chinese).
[8] 李正周, 刘国金. 基于均值漂移和卡尔曼滤波的目标跟踪方法[J]. 弹箭与制导学报, 2008, 28(1): 71-74.
LI Z Z, LIU G J. Target tracking based on mean-shift and Kalman filter[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2008, 28(1): 71-74 (in Chinese).
[9] 沈悦, 张雷, 傅忠谦, 等. 区间卡尔曼滤波算法在高动态导航的研究[J]. 宇航学报, 2013, 34(3): 355-361.
SHEN Y, ZHANG L, FU Z Q, et al. Interval Kalman filtering algorithm for high dynamic navigation and positioning[J]. Journal of Astronautics, 2013, 34(3): 355-361 (in Chinese).
[10] 崔乃刚, 张龙, 王小刚, 等. 自适应高阶容积卡尔曼滤波在目标跟踪中的应用[J]. 航空学报, 2015, 36(12): 3885-3895.
CUI N G, ZHANG L, WANG X G, et al. Application of adaptive high-degree cubature Kalman filter in target tracking[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(12): 3886-3895 (in Chinese).
[11] 于浛, 魏喜庆, 宋申民, 等. 基于自适应容积卡尔曼滤波的非合作航天器相对运动估计[J]. 航空学报, 2014, 35(8): 2251-2260.
YU H, WEI X Q, SONG S M, et al. Relative motion estimation of non-cooperative spacecraft based on adaptive CKF[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(8): 2251-2260 (in Chinese).
[12] 李理敏, 龚文斌, 刘会杰, 等. 基于自适应扩展卡尔曼滤波的载波跟踪算法[J]. 航空学报, 2012, 33(7): 1319-1328.
LI L M, GONG W B, LIU H J, et al. A carrier tracking algorithm based on adaptive extend Kalman filter[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(7): 1319-1328 (in Chinese).
[13] 李文, 李清东, 李亮, 等. 基于模糊自适应卡尔曼滤波的大气数据辅助姿态算法[J]. 航空学报, 2015, 36(4): 1267-1274.
LI W, LI Q D, LI L, et al. Air data assisted attitude algorithm based on fuzzy adaptive Kalman filter[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(4): 1267-1274 (in Chinese).
[14] 魏喜庆, 宋申民. 基于改进容积卡尔曼滤波的奇异避免姿态估计[J]. 航空学报, 2013, 34(3): 610-619.
WEI X Q, SONG S M. Improved cubature Kalman filter based attitude estimation avoiding singularity[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(3): 610-619 (in Chinese).
[15] 吴楠, 陈磊. 高超超声速滑翔再入飞行器弹道估计的自适应卡尔曼滤波[J]. 航空学报, 2013, 34(8): 1960-1971.
WU N, CHEN L. Adaptive Kalman filtering for trajectory estimation of hypersonic glide reentry vehicles[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(8): 1960-1971 (in Chinese).
[16] LIU Y, DONG K, WANG H P, et al. Adaptive Gaussian sum squared-root cubature Kalman filter with split-merge scheme for state estimation[J]. Chinese Journal of Aeronautics, 2014, 27(5): 1242-1250.
[17] 王琪. 基于惯性测量的全舰统一姿态基准技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2007: 5-15.
WANG Q.Research of unified attitude reference technology of the whole ship based on inertial measurement[D].Harbin: Harbin Engineering University,2007:5-15(in Chinese).
[18] 王跃钢, 杨家胜, 杨波. 维度未知条件下捷联惯导系统晃动基座的初始对准[J]. 航空学报, 2012, 33(12): 2322-2329.
WANG Y G, YANG J S, YANG B. SINS initial alignment of swaying base under geographic latitude uncertainty[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(12): 2322-2329 (in Chinese).
[19] 刘占超, 房建成. 基于双捷联算法的POS误差在线标定方法[J]. 航空学报, 2012, 33(9): 1679-1687.
LIU Z C, FANG J C. Online calibration of POS error based on double strapdown algorithm[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(9): 1679-1687 (in Chinese).
[20] 谢阳光, 伊国兴, 王常虹, 等. 高斯-厄米特滤波器在捷联惯导系统初始对准中的应用[J]. 航空学报, 2012, 33(3): 554-560.
XIE Y G, YI G X, WANG C H, et al. Application of Gauss-Hermit filter in SINS alignment[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(3): 554-560 (in Chinese).
[21] 刘言. 基于光纤陀螺舰载捷联垂直基准关键技术研究[D]. 哈尔滨: 哈尔滨工业大学, 2011: 23-29.
LIU Y. The research on the shipboard strapdowm vertical reference unit based on fiber optic gyroscope[D]. Harbin: Harbin Institute of Technology, 2011: 23-39 (in Chinese).
(责任编辑: 苏磊)
Influence of platform swaying on accuracy of Kalman filter tracking
CHENGHan*,CHENWeiyi,XIEZhiliang
DepartmentofWeaponEngineering,NavalUniversityofEngineering,Wuhan430033,China
The model for the target relative movement coordinate system and movement tracking is built to study the influence of platform swaying on the target’s movement status captured by the tracking system. Base on the theory of strapdown vertical datum system compensating, the compensating model for the swaying angle is developed. The compensating model is applicable for the strapdown vertical datum system after theoretical derivation of the compensating algorithm. The influence on accuracy of Kalman filter tracking of platform swaying is analyzed by contrasting the difference between different tracking modes of compensating. The main influence on the accuracy of Kalman filter tracking under the condition of platform swaying is figured out to be the increase of model error, which may cause the divergence of the filter. The simulation model is built to prove the correctness of the conclusion, and the simulation result can provide theoretical reference for improving the ship-based tracking theory.
platform swaying; relative movement tracking model; strapdown vertical datum system; Kalman filter tracking; model error
2016-07-06;Revised2016-08-10;Accepted2016-09-05;Publishedonline2016-09-201009
2016-07-06;退修日期2016-08-10;录用日期2016-09-05; < class="emphasis_bold">网络出版时间
时间:2016-09-201009
www.cnki.net/kcms/detail/11.1929.V.20160920.1009.002.html
*
.E-mail843740845@qq.com
程晗, 陈维义, 谢芝亮. 平台摇摆对卡尔曼滤波跟踪精度的影响J. 航空学报,2017,38(6):320589.CHENGH,CHENWY,XIEZL.InfluenceofplatformswayingonaccuracyofKalmanfiltertrackingJ.ActaAeronauticaetAstronauticaSinica,2017,38(6):320589.
http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn
10.7527/S1000-6893.2016.0249
V448.2; TP237; TP391.9
A
1000-6893(2017)06-320589-10
URL:www.cnki.net/kcms/detail/11.1929.V.20160920.1009.002.html
*Correspondingauthor.E-mail843740845@qq.com

