挠性航天器刚性-柔性耦合动力学模型控制方法
张恒浩 王小锭 张 霞 魏 明 陈春燕
中国运载火箭技术研究院研究发展中心,北京100076
挠性航天器刚性-柔性耦合动力学模型控制方法
张恒浩 王小锭 张 霞 魏 明 陈春燕
中国运载火箭技术研究院研究发展中心,北京100076
针对挠性航天器本身大范围刚性运动和携带载荷进行动态变形运动的耦合问题,建立一种动力学刚性-柔性耦合模型运动控制方法。该方法通过计算航天器所受的惯性力来推导挠性梁等效弯曲刚度,建立一个物理意义明晰并且耦合度低的动力学模型,能够全面分析对挠性梁的各种耦合干扰影响。仿真结果表明,建立的刚性-柔性耦合动力学模型能够对挠性梁进行全面控制分析,并通过调整相关参数有效控制耦合干扰项对挠性梁振动的影响。
挠性航天器;刚性-柔性耦合;动力学建模;挠性梁
在空间工作过程中,挠性航天器最主要的力学特征是自身具有大范围刚性运动,同时伴有携带载荷的动态变形运动,这2种运动在整个航天器空间工作时一直相互耦合[1]。这种耦合特征的动力学控制与在理想状态下的动力学控制有本质区别,设计挠性航天器动力学控制方法的核心在于解决中心部件的大范围刚性位移和附加载荷小范围动态变化位移之间的强耦合问题[2-5]。
挠性航天器刚性-柔性动力学设计的理论基础起源于美国科学家Kane,他在1987年首次提出动力学刚性化概念。当航天器的挠性梁旋转速度越快时,挠性梁在横向方向具有的振动刚度越大[6]。基于这一基础原理,本文对固定在航天器上的挠性梁采用一种新的控制方法。采用广义相对论将引力场和加速度场进行关联,力学模型在惯性坐标系下使用加速度物理量;在非惯性坐标系下使用引力场物理量。这样可以将非惯性系统力学控制问题转化到惯性系中进行解算[7]。国内方面,浙江大学王光庆等提出了一种柔性解耦动力学模型控制方法,可以同时实现对柔性臂末端运动轨迹的定位控制和弹性振动抑制控制。刘志全等建立了复杂关节精细动力学模型,用于解决航天器刚度与扭曲变形精度耦合分析。
本文将航天器和其携带的有效载荷作为一个整体进行动力学建模控制。整个控制过程重点分析挠性梁和梁上附加的有效载荷振动控制。控制方法首先对挠性梁进行位置区间划分,借助Heaviside函数将有效载荷引起的导致梁的受力分布推导为分段连续函数,并引入Dirac函数进行刚性-柔性动力学建模[8]。
1 控制方法设计
控制方法的应用对象为航天器和其搭载的有效载荷组合体。考虑实际工程中对航天器载荷搭配需求,规定搭载的有效载荷位于挠性梁上非顶端位置之外的其他任何位置[9]。控制方法将根据这一组合体系进行刚性-柔性动力学建模控制。
根据应用对象特点,当航天器在空间进行姿态和轨道机动时,航天器的挠性梁动态变形如图1所示。
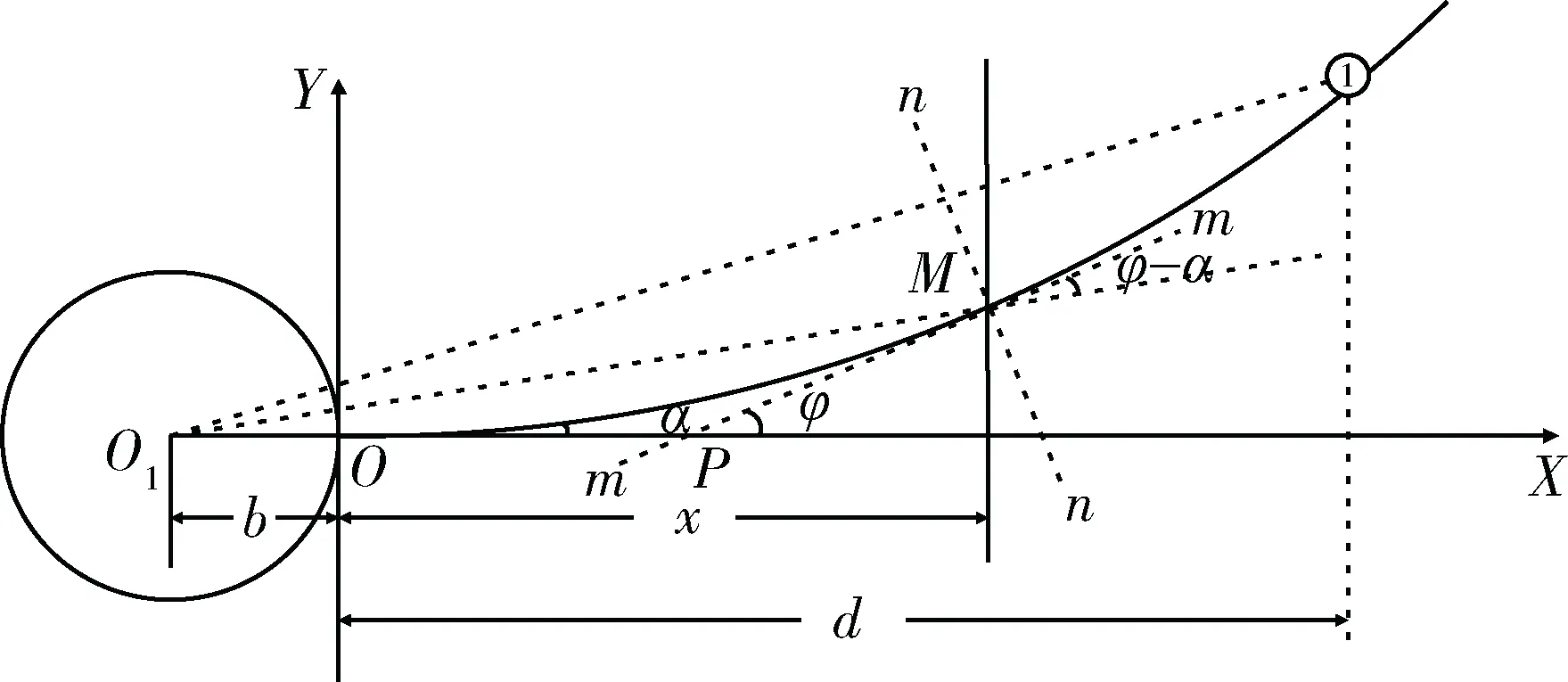
图1 航天器挠性梁动态变形示意图
从图1可以看出,随着航天器的运动,挠性梁在发生横向振动的瞬时出现了结构上的变形弯曲。横向弯曲变形是挠性梁动力学建模分析的主要原因,在控制方法设计过程中可以忽略梁体纵向上的变形情况。图中,设d是有效载荷在梁上的位置,载荷质量为mt,引起的转动惯量为It。根据Hub提出的载重梁系统动力学分析,在这种情况下挠性梁共承担3种载荷形式:1)自身质量的惯性分布;2)附在梁上的载荷引起的惯性力;3)附在梁上的载荷引起的惯性力矩。载荷在梁上位置产生的惯性力相对挠性梁法向n-n方向上的代数分量如式(1):

(1)
当航天器转动时,由载荷转动惯量产生的力矩计算如式(2):
(2)
因此载荷在航天器挠性梁上的垂直方向分量表示如图2所示。
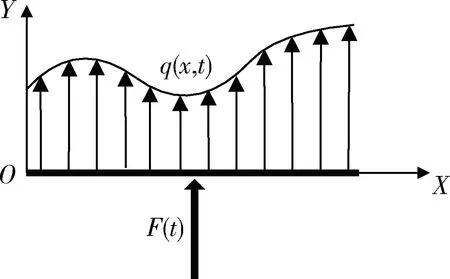
图2 载荷在挠性梁上分布图示
根据图2所示,将在挠性梁上的分布载荷设为q(x,t),载荷在梁上产生的惯性力为F(t),其作用点是梁上搭载载荷的位置。在整个航天器挠性梁上,以x=d为分界点分为2段,给出梁上受力的分布函数如方程组(3),梁上受力矩的分布函数如方程组(4):
(3)

(4)
引入Heaviside函数,方程组(3)转化为式(5),方程组(4)转化为式(6):
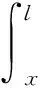
(5)
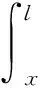
(6)
当航天器进行姿轨运动时,挠性梁承受的弯矩通过式(7)得到:
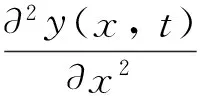
(7)
将式(6)代入式(7),2次对位置变量进行偏导计算,得到挠性梁在横向方向的动力学振动方程式(8):

(8)
式(8)中的未知参数由方程组式(9)计算:
(9)
整理式(8)和(9),得到式(10):

(10)
因为航天器携带载荷在空间进行运动时,自身大范围刚性运动和载荷引起梁体柔性变形运动一直在相互耦合。在航天器系统中,刚性运动和柔性运动交汇点处受到的外力和外力矩计算如方程组式(11):
(11)
根据在挠性梁上产生的载荷分布函数,将方程组式(11)与方程组式(3)和(4)进行整合,视整个航天器系统为一个刚体系统,因此作用在该系统上所有力矩之和由式(12)得到:
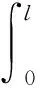
(12)
整个航天器在工作时总的转动惯量设为Jall,通过方程组(13)计算:
(13)
结合式(11)~(13),得到航天器系统的动力学模型方程式(14):
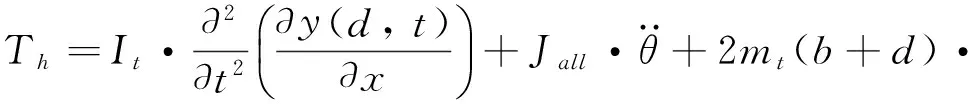
(14)


从刚性-柔性耦合动力学模型控制方法中可以明显看出:当航天器的挠性梁发生横向振动时,由于内力和内力矩分布作用,在梁的刚性运动和柔性运动交汇点,挠性梁会对航天器产生反作用力,影响航天器的姿轨运动。方法中还给出了航天器系统的动力刚化计算项。整个动力学模型中体现了由于航天器受力刚化导致挠性梁在非惯性系下产生的离心力与整个梁在横向振动过程中的影响关系。
综上可见,提出的刚性-柔性耦合动力学模型控制方法清楚地展示了航天器携带的载荷对挠性梁横向振动的影响,并考虑了科氏惯性力对挠性梁横向振动的影响。在工程应用中针对影响振动的因素进行相应设计,使飞行器本体有效抑制自身扰动,完成姿态和轨道任务工作。
2 计算结果分析
工程应用中,载有有效载荷的航天器各种参数条件如表1所示。
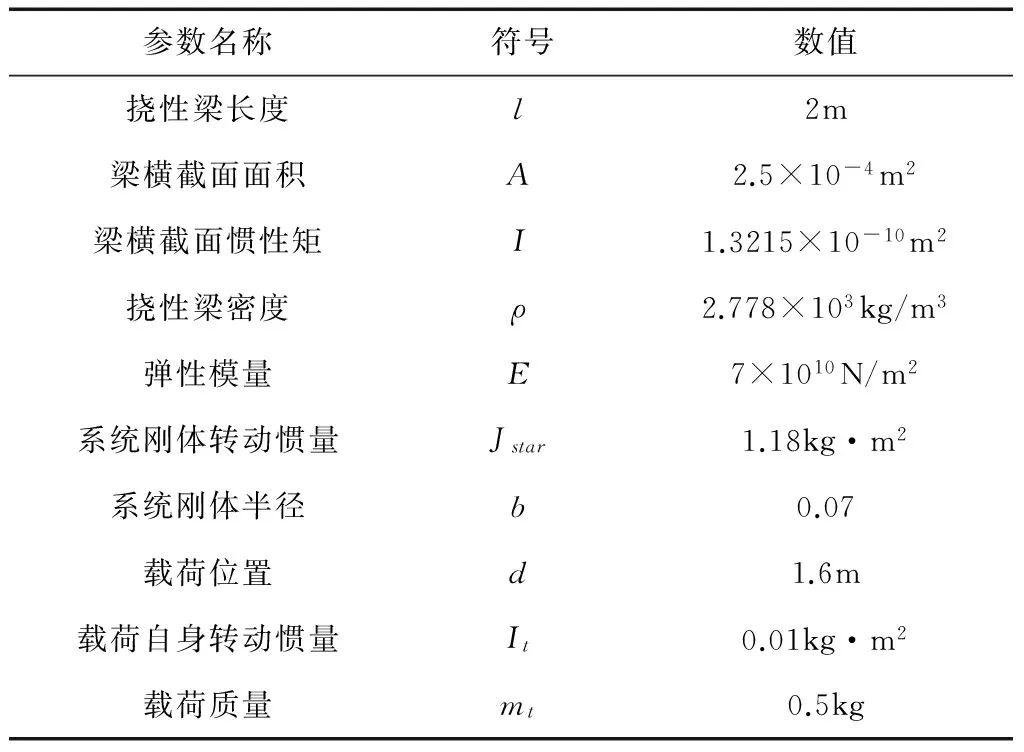
表1 携带载荷航天器参数表
挠性梁的固有频率设为0.6rad/s,根据工程要求,航天器系统工作的角速度频率范围必须明显远离梁本身固有振动频率。设航天器的最终角速度频率为0.0995Hz。将航天器系统整体看做一个刚体,系统姿态角的速度变化比例设为2。表2给出控制方法计算得到的载荷在挠性梁相关位置上对其横向振动的影响情况。
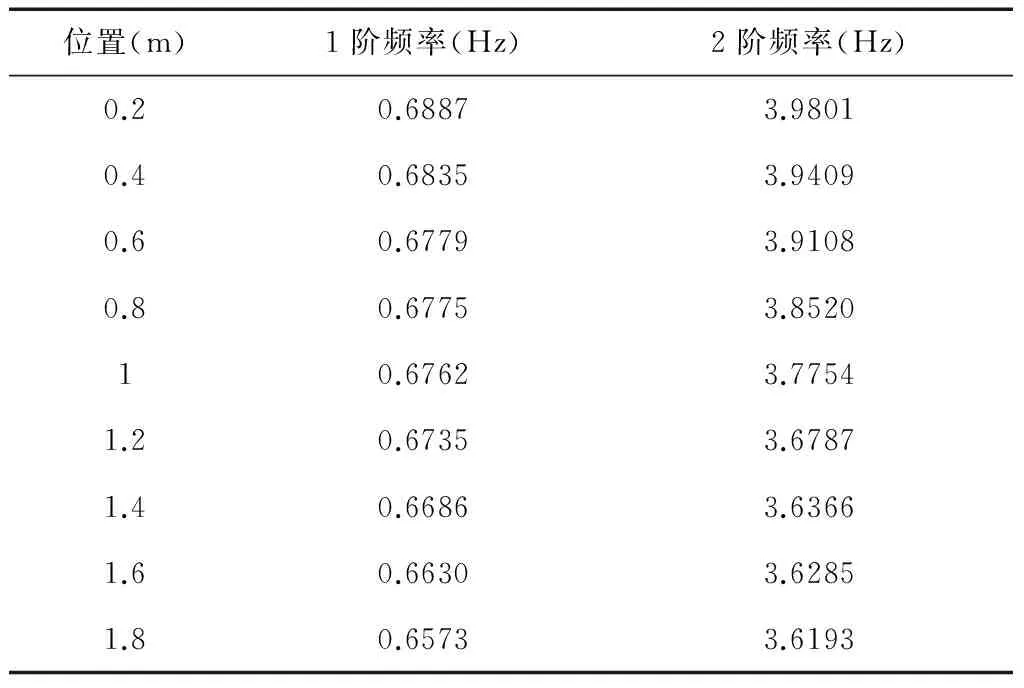
表2 负载对挠性梁横向振动影响表
图3~5给出了挠性航天器系统自由振荡频率分别在1.6rad/s,3rad/s和3.6rad/s的振荡条件下,考虑耦合关系和不考虑耦合关系2种情况下计算得到的挠性梁横向振动情况。

图3 振动频率为1.6rad/s条件下挠性梁振动示意图
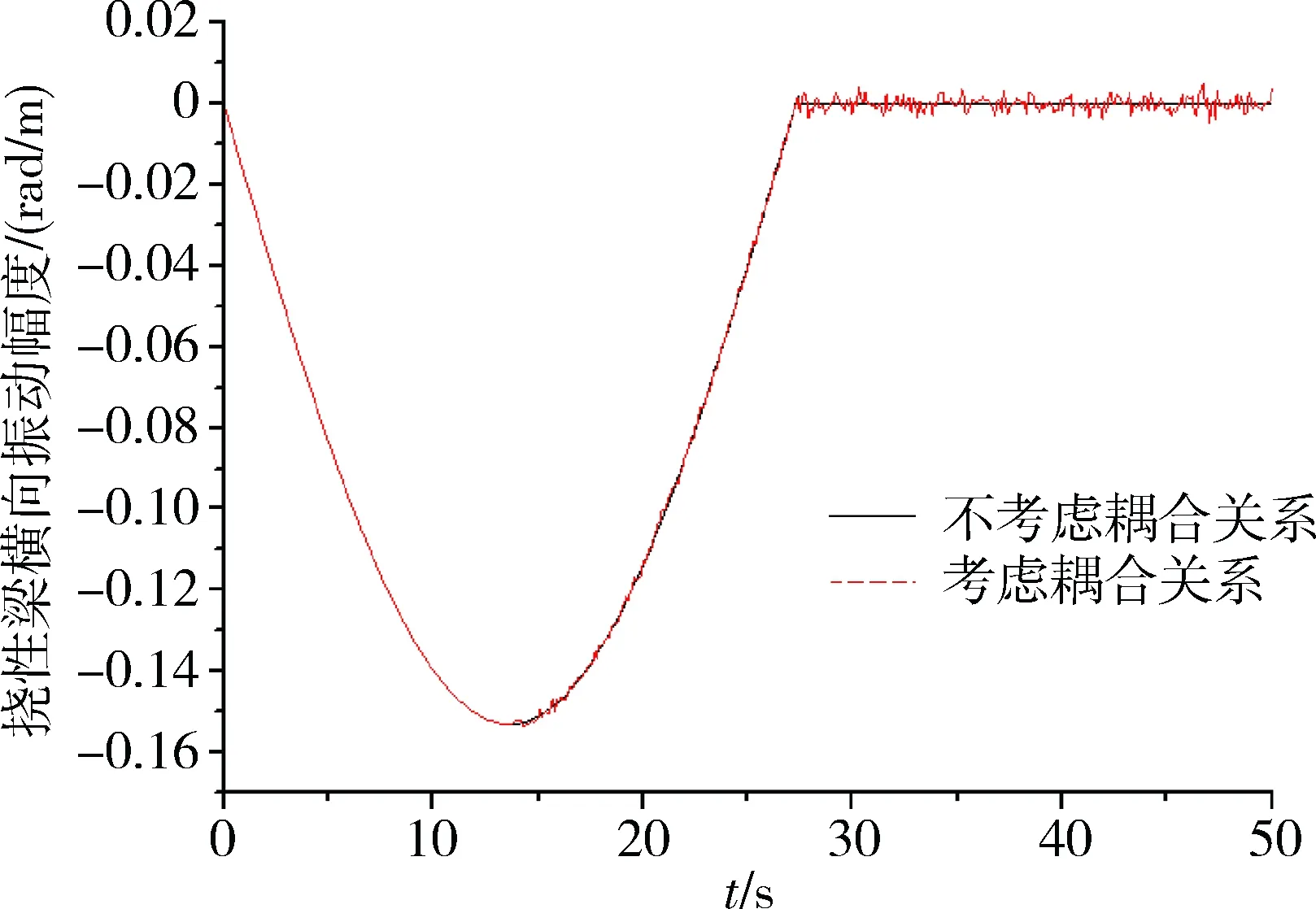
图4 振动频率为3rad/s条件下挠性梁振动示意图
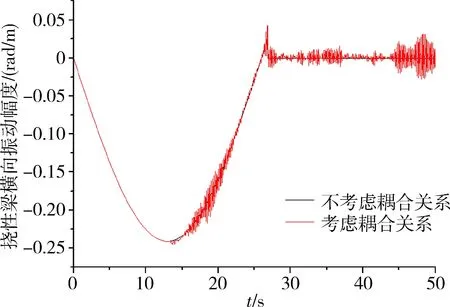
图5 振动频率为3.6rad/s条件下挠性梁振动示意图

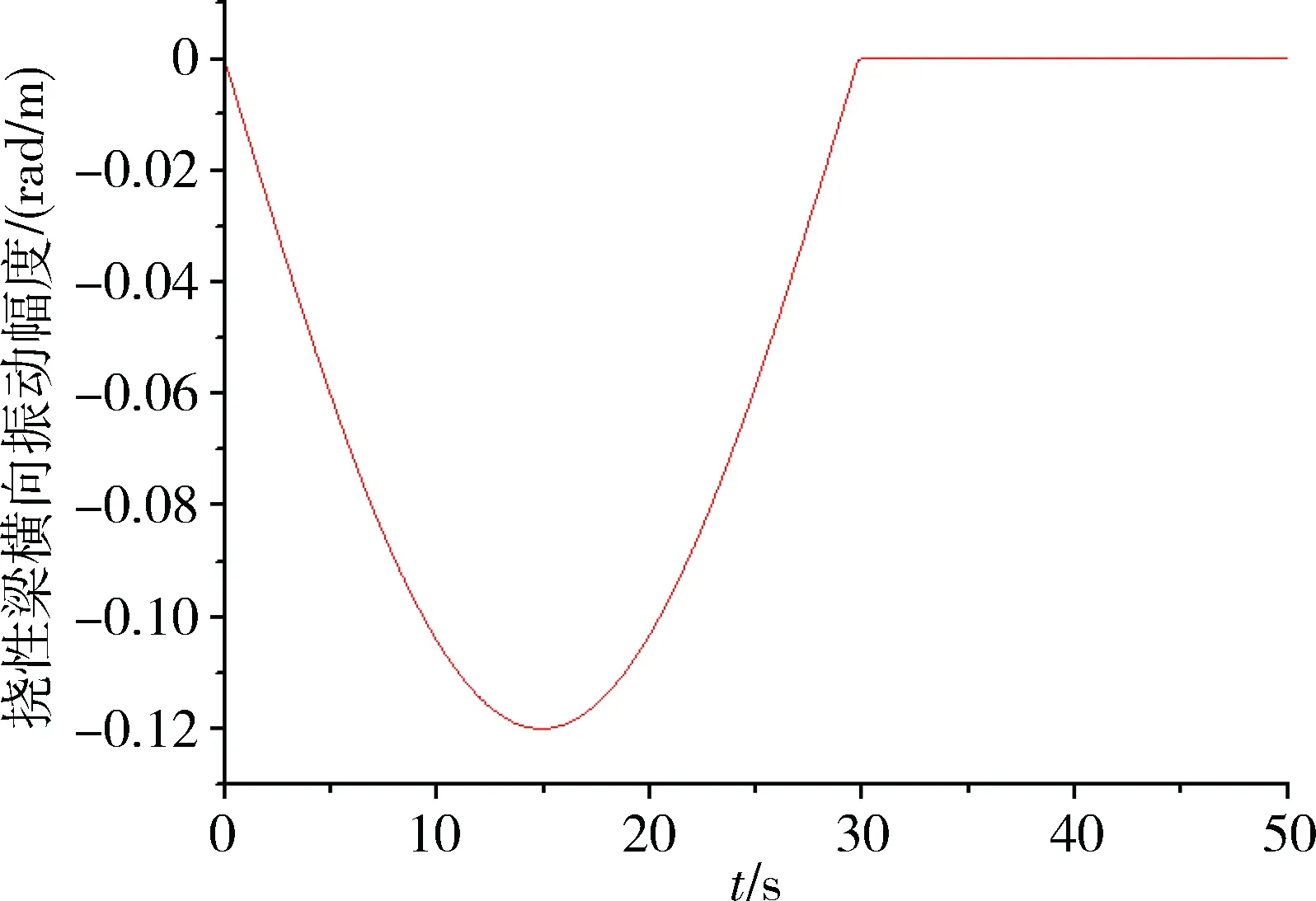
图6 抑制耦合干扰后1.6rad/s条件下挠性梁振动示意图
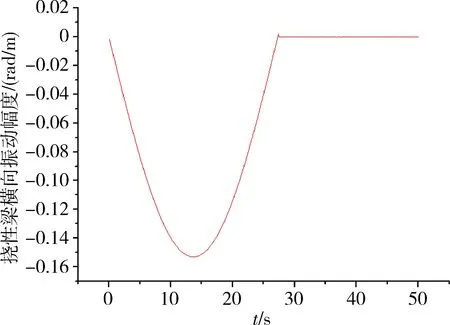
图7 抑制耦合干扰后3rad/s条件下挠性梁振动示意图
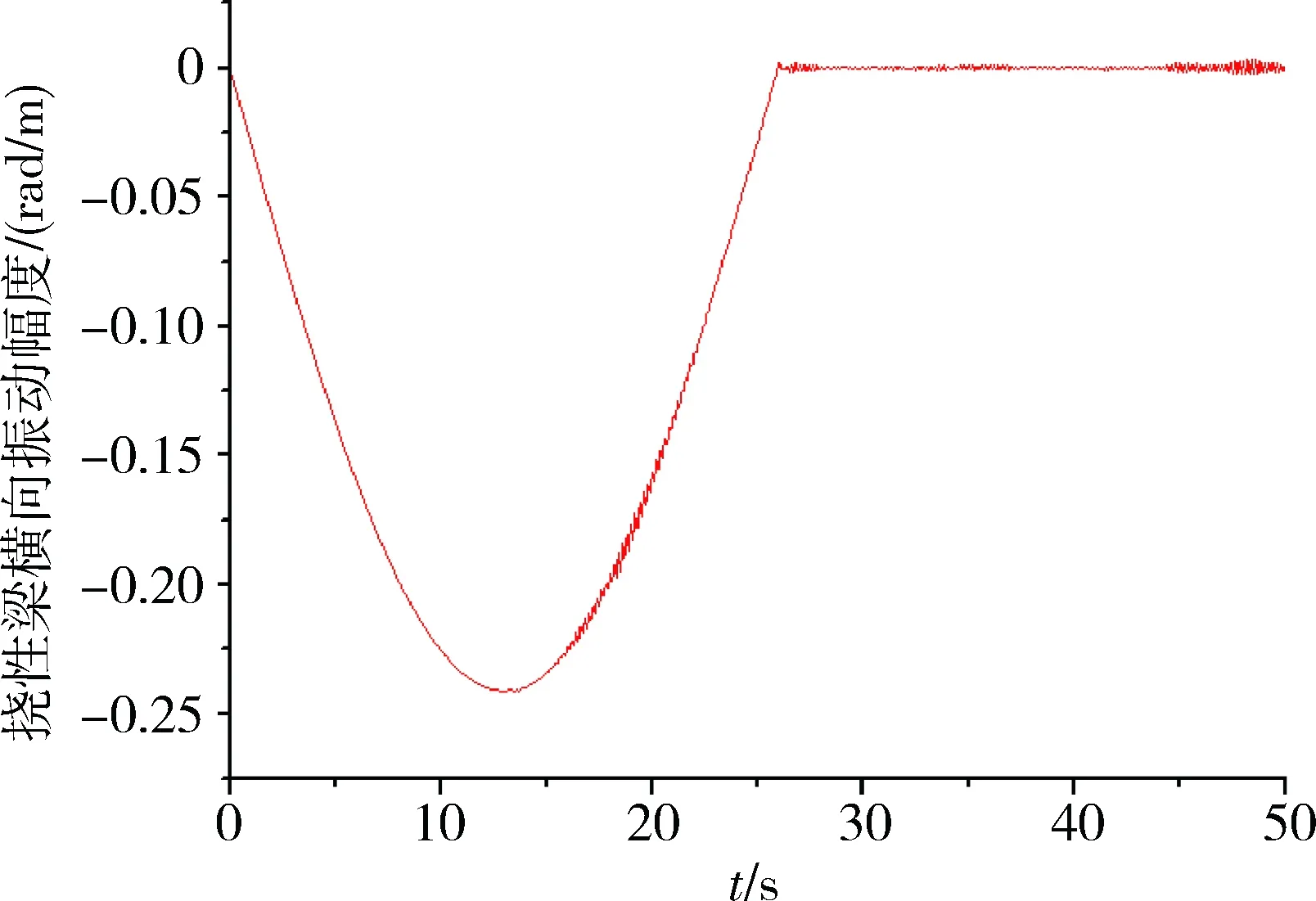
图8 抑制耦合干扰后3.6rad/s条件下挠性梁振动示意图
从图6~8可明显看出,根据方程(14)对耦合项干扰进行抑制后,航天器挠性梁在工作过程中的振动干扰明显减弱。说明本文提出的刚性-柔性耦合动力学模型能对挠性梁的控制过程进行全面分析,并能有效抑制干扰对梁的振动影响,所得模型物理意义明确,从理论上解释了附加载荷和梁本身质量分布以及科氏惯性力对挠性梁振动的耦合影响。
3 结论
针对挠性航天器本身大范围刚性运动和携带载荷进行动态变形运动的耦合问题,建立一个物理意义明晰并且耦合度低的动力学模型,能全面分析对挠性梁的各种耦合干扰原因,通过耦合度低的物理模型调整相关参数可有效实现耦合干扰对梁的振动影响。
[1] 戈新生, 刘延柱. 万有引力场中带挠性轴太阳帆板航天器的姿态稳定性[J]. 空间科学学报,1999, 14(4): 349-353. (Ge Xinsheng, Liu Yanzhu. Attitude Stability of Solar Wings on Spacecraft with a Flexible Shaft in Gravitational Field[J]. Journal of Space Science,1999, 14(4): 349-353.)
[2] Zhang Jianying, Liu Tun. Study on Component Synthesis Active Vibration Suppression Method Using Zero-placement Technique[J]. Chinese Journal of Aeronautics, 2008, 21(3):304-312.
[3] 李箐. 充液挠性系统动力学分析及在航天工程中的应用研究[D]. 清华大学, 2010.
[4] 周莎, 张伟, 姚明辉. 大型空间挠性天线结构弯曲振动的多脉冲混沌动力学研究[C]. 第十五届全国非线性振动暨第十二届全国非线性动力学和运动稳定性学术会议.
[5] 肖世富, 陈学前, 刘信恩. 简支-挠性支撑梁的振动特性与轴向压缩稳定性研究[J]. 北京大学学报, 2016, 52(4): 699-707. (Xiao Shifu, Chen Xueqian, Liu Xinen. Study on the Vibration Characteristic and Axial-Compressive Stability of the Beam with Simple and Flexible Supports[J]. Acta Scientiarum Naturalium Universitatis Pekinensis, 2016, 52(4): 699-707.)
[6] 万九卿. 基于前馈补偿的高精度卫星姿态控制[J]. 宇航学报, 2006, 27(6): 1393-1396. (Wan Jiuqing. High Precision Satellite Attitude Control Based on Feedforward Compensation[J]. Journal of Astronautics, 2006, 27(6): 1393-1396.)
[7] 周连军. 基于遗传算法的挠性航天器大角度机动的变结构控制[J]. 上海航天, 2005 (1): 15-18.
[8] 汪飞舟. 控制输入受限的挠性航天器有限时间姿态控制[J]. 航天控制, 2016, 34(5): 59-69.(Wang Feizhou. Finite-time Attitude Control of Flexible Spacecraft under Actuator Saturation[J]. Aerospace Control, 2016, 34(5): 59-69.)
[9] 王新民. 转动载荷对卫星姿态的影响与控制研究[J]. 空间控制技术与应用, 2016, 42(5): 14-18.(Wang Xinmin. On the Influence of Rotatable Payload and Control for Satellite Attitude[J]. Aerospace Control and Application, 2016, 42(5): 14-18.)
TheControlWayofFlexibleSpacecraftRigid-FlexibleCoupleDynamicModel
Zhang Henghao,Wang Xiaoding, Zhang Xia, Wei Ming, Chen Chunyan
R&D Center, China Academy of Launch Vehicle Technology, Beijing 100076, China
Regardingthecoupleproblemofflexiblespacecraft’slargecategorymovementandload’sdynamictransformermovement,arigid-flexiblecontrollerincludescraft,flexiblebeamandloadisdesigned.Inthisdesign,theinertia-forceisusedtocomputerigidanddynamicmodelissetupwhichhaslowercoupleandphysicsmeaning,whichconsiderallcoupledisturbsroundlyandrestraintheinterferentialeffects.Thesimulationresultshowsthatsettingupawholecraft-flexiblebeam-loadsystemcananalyseflexiblebeamworkingprocessroundlyandcanrestraincoupleinterferenceclearlywithsomeparametersadjusted.
Flexiblespacecraft;Rigid-flexiblecouple;Dynamicmodel;Flexiblebeam

V448
A
1006-3242(2017)05-0045-06
2017-04-18
张恒浩(1982-),男,河北人,博士,高级工程师,主要研究方向为飞行器总体控制、电气总体设计;王小锭(1983-),男,福建人,硕士,高级工程师,主要研究方向为飞行器电气总体设计;张霞(1983-),女,重庆人,硕士,高级工程师,主要研究方向为飞行器电气总体设计;魏明(1982-),男,江西人,硕士,工程师,主要研究方向为飞行器电气总体设计;陈春燕(1982-),女,江西人,硕士,高级工程师,主要研究方向为飞行器电气总体设计。

