基于车轨耦合的弹性地基梁板模型及算法*

陈龙川 雷晓燕

基于车轨耦合的弹性地基梁板模型及算法*

陈龙川 雷晓燕**

（华东交通大学铁路环境振动与噪声教育部工程研究中心，330013，南昌//第一作者，硕士研究生）

板式无砟轨道具有变形小、稳定性好的优点，在我国铁路客运专线上应用广泛。国内外学者在建立车辆、轨道以及车辆-轨道耦合系统模型及算法方面已做了许多工作。然而，已有的模型与实际情况尚有差异，有待进一步完善。根据板式无砟轨道的结构特点，采用板单元模拟轨下结构，建立了车辆-板式轨道耦合系统动力分析模型及算法，推导了板式轨道模型单元的刚度、质量以及阻尼矩阵；考虑轮轨非线性接触行为，引入交叉迭代法求解车辆-轨道耦合系统动力学方程；仿真分析了线路随机不平顺工况下，CRH3型动车通过CRTSⅡ型板式无砟轨道时，车辆和轨道结构的动力响应。该模型与算法比已有模型更接近实际，计算结果更准确可靠。

板式轨道；车辆-轨道耦合系统；交叉迭代法；动力响应

板式无砟轨道具有变形小、稳定性好的优点，在我国铁路客运专线上应用广泛。国内外众多学者通过建立车辆模型、轨道模型和车辆-轨道系统模型［1-2］来分析车辆轨道动力特性。文献［3］建立了轨道-路基有限元模型，分析了高速列车运行过程中，轨道和路基竖向位移在时间和空间上的分布规律；文献［4］采用ABAQUS软件建立轨道下部结构的有限元模型，分析了在不同运行速度下轨道结构的动力特性；文献［5］采用3层梁单元模拟轨道，建立了车辆-轨道系统模型，并对轨道过渡段动力特性进行分析；文献［6］将弹性支承块式无砟轨道离散为24个自由度的轨段单元，建立了高速列车-轨道耦合模型并进行动力性能分析；文献［3-4］采用有限元软件建模，将轮轨相互作用简化为作用在轨道上的荷载；文献［5］将轨下轨道板和混凝土底座模拟为梁单元，但该计算模型存在计算效率不高，不能反映车辆轨道相互作用特点的问题。

本文根据板式无砟轨道的结构特点，采用板单元模拟轨下结构，建立了分析车辆-板式轨道耦合系统的动力分析模型及算法，推导得出板式轨道单元的刚度、质量以及阻尼矩阵；考虑了轮轨非线性接触行为；不同于文献［6］的Wilson-θ，引入交叉迭代法求解车辆-轨道耦合系统动力学方程，提高了计算效率；分析了线路随机不平顺工况下，CRH3型动车通过CRTSⅡ型板式无砟轨道时，车辆和轨道结构的动力响应。该模型与算法更接近实际，计算结果更准确、可靠。

1 模型理论

1.1 基本假设

本模型作了以下基本假设：

（1）考虑车辆和轨道的竖向动力作用；

（2）上部车辆单元与下部轨道单元沿轨道方向对称，结构模型可取半计算；

（3）采用附有二系悬挂体系的多刚体系统模拟车辆单元，车体与转向架具有竖向与点头振动；

（4）考虑轮轨之间的非线性接触耦合行为；

（5）采用离散、弹性支承的二维梁单元模拟钢轨，轨下垫板与扣件系统的支承弹性系数及阻尼系数分别用ky1和cy1表示；

（6）采用连续、弹性支承的三维板单元模拟轨道板，轨道板下CA（水泥沥青）砂浆层的支承弹性系数与阻尼系数分别用ky2和cy2表示；

（7）采用连续、弹性支承的三维板单元模拟混凝土底座，混凝土底座下路基的支承弹性系数与阻尼系数分别用ky3和cy3表示。

1.2 车辆单元

将车辆视为具有二系悬挂弹簧阻尼10个自由度的多刚体结构单元。其中，车体和转向架具有竖向和点头运动、每个轮对具有竖向运动。车辆单元模型如图1所示。图1中：Mc、Jc分别为结构模型取半后的车体质量与转动惯量；Mt、Jt分别为结构模型取半后的转向架质量与转动惯量；ks1、ks2分别为车辆一、二系悬挂刚度；cs1、cs2分别为车辆一、二系悬挂阻尼；Mwi（i=1、2、3、4）为第i个车轮的质量；Vc、φc分别为车体竖向运动的竖向位移、点头运动的角位移；Vti、φti（i=1、2）分别为第i个转向架竖向运动的竖向位移、点头运动的角位移；vwi（i=1、2、3、4）为第i个车轮的竖向位移；Fuli（i=1、2、3、4）为第i个车轮的轮轨接触力；Rw为轮轨接触系数。考虑轨道的随机不平顺，η1、η2、η3、η4分别表示轨道与 4 个车轮接触处的不平顺幅值。

定义车辆单元的位移为：

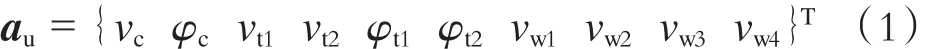
车辆单元模型的刚度、质量以及阻尼矩阵的推导和动力解析方程的建立见文献［7-8］。

图1 车辆单元模型

1.3 轨道单元

板式无砟轨道的主要结构为钢轨、垫板扣件系统、轨道板、CA砂浆层以及混凝土底座。文献［5］采用梁单元模拟轨道板和底座，但其与实际结构特性和受力性状不符。本文建立模型时，考虑轨道板与底座的横向转角，采用板单元模拟轨道板和底座，弹簧阻尼模拟扣件、CA砂浆和路基。每1个轨道单元由1个梁单元和4块板单元组装而成，将轨道离散成40个自由度的轨道单元。轨道单元模型如图2所示。图2 中：w1、w8分别表示钢轨的竖向位移；θ1y、θ8y分别表示纵向钢轨的转角；wi（i=2、3、4、9、10、11）表示轨道板的竖向位移；θix、θiy（i=2、3、4、9、10、11）分别表示轨道板横向、纵向转角；wi（i=5、6、7、12、13、14）表示混凝土底座的竖向位移；θix、θiy（i=5、6、7、12、13、14）分别表示混凝土底座横向、纵向转角。

图2 轨道单元模型

定义轨道单元的位移为：

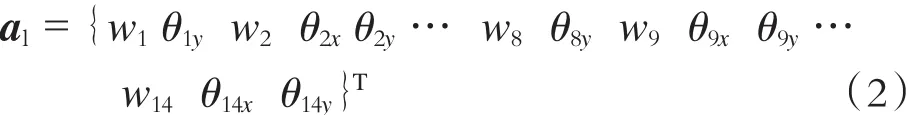
根据拉格朗日方程，建立轨道单元的有限元方程为：

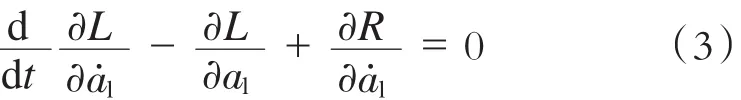
式中：

L——拉格朗日函数；

T，Πp，R——动能、弹性势能以及耗散能。

运用有限元方法推导钢轨、轨道板以及混凝土底座的动能、弯曲势能以及耗散能，计算钢轨、轨道板以及混凝土底座的刚度、质量和阻尼矩阵。采用对号入座的方法嵌入形成轨道单元的刚度矩阵kl，e、质量矩阵 ml，e和阻尼矩阵 cl，e。

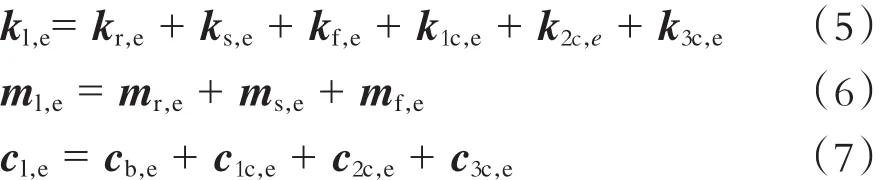
式中：

kr，e，ks，e，kf，e——钢轨、轨道板以及混凝土底座的弯曲势能产生的单元刚度矩阵；

kic，e——第i层支承的单元刚度矩阵（i=1、2、3）；

mr，e，ms，e，mf，e——钢轨、轨道板以及混凝土底座的弯曲动能产生的单元质量矩阵；

cic，e——第i层支承的单元阻尼矩阵（i=1、2、3）；

cb，e——与单元质量矩阵、单元刚度矩阵有关的单元比例阻尼。

以式（5）～式（7）的各组成项可通过以下式（8）～式（11）进行计算。

式中：

Er，Ir，Ar——钢轨弹性模量、惯性矩和截面积；

a，b，hs，hf——板单元的长度、宽度，轨道板和混凝土底座的厚度；

ρs，ρr， ρf——钢轨、 轨道板和混凝土底座的密度；

B——弯曲矩形板单元的应变矩阵；

D——弯曲矩形板单元的弹性矩阵；kyi（i=1，2，3）、cyi（i=1，2，3）——第i层支承的刚度系数、阻尼系数；

N1，N2，N3，Nr，Ns，Nf——插值函数矩阵。

1.4 车辆-轨道耦合

通过组装轨道单元的刚度矩阵kl，e、质量矩阵ml，e、阻尼矩阵 cl，e得到整个轨道的刚度矩阵 Kl、质量矩阵Ml以及阻尼矩阵Cl。车辆以及轨道子系统的动力学方程为：

其中：

式中：

Ku，Mu，Cu——车辆的刚度、质量以及阻尼矩阵；

Qlg，Qug——轨道、车辆系统的重力向量；

Ful——轮轨之间作用力。

两个子系统通过非线性轮轨力耦合，利用交叉迭代算法进行求解，计算步骤详见文献［8］。

2 模型验证与仿真分析

根据上述模型和算法，用Matlab编制计算程序，运用所开发的程序进行算例验证和仿真分析。

2.1 模型验证

为验证本文模型的正确性，与文献［9］中的模型算例进行对比。本文选用1节CRH2型动车，车速为300 km/h，同时考虑德国低干扰不平顺谱来建立模型。且将本文模型的计算结果与文献［9］模型计算结果和实测结果进行对比，如表1所示。图3为本文模型与文献［9］的钢轨挠度曲线对比图。由图3可知，两者峰值接近、波形吻合，证明了本文模型的正确性。

表1 模型计算结果与文献［9］计算结果、实测结果对比

2.2 仿真分析

利用所建立的车辆-轨道耦合系统动力分析模型，进行线路不平顺工况下车辆和轨道竖向动力响应分析。轨道参考CRTSⅡ型板式无砟轨道，车辆参考CRH3型动车，计算参数见文献［5］。线路总计算长度为300 m，共划分为462个轨道单元，3 234个节点，9 240个自由度，时间步长取0.001 s。车速200 km/h，线路不平顺采用美国6级谱。整车高速通过210 m位置时，部分具有代表性的轨道、车辆振动响应时程曲线如图4～11所示。

图3 钢轨挠度曲线对比图

图4 钢轨竖向位移

图5 钢轨竖向加速度

图6 轨道板竖向位移

图7 轨道板竖向加速度

图8 车体竖向加速度

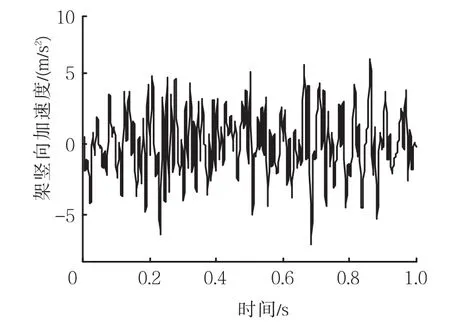
图9 转向架竖向加速度

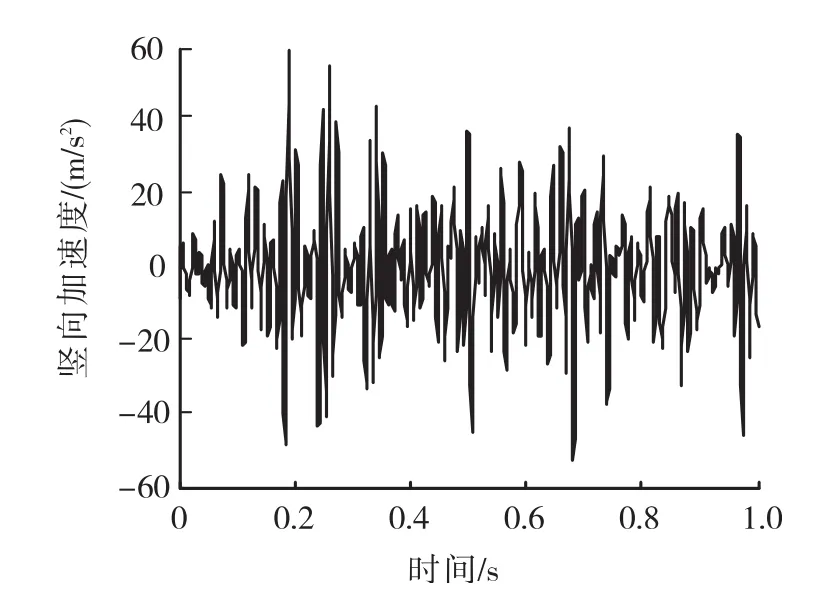
图10 车轮竖向加速度

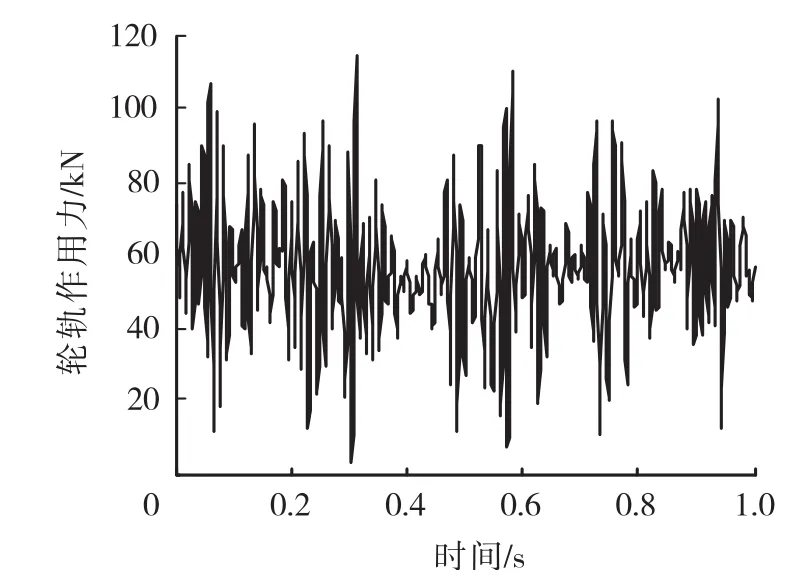
图11 轮轨作用力

表2与表3分别为在线路平顺和不平顺工两种况下，轨道结构振动响应和车辆加速度的幅值。从表2中可见：由线路不平顺引起的轨道结构竖向位移增幅为钢轨在 20%左右，轨道板、混凝土底座在 10%左右；由线路不平顺引起的轨道结构加速度的增幅为钢轨、轨道板在 80倍左右，混凝土底座在 40倍左右。由此可见：线路不平顺对路基上 CRTSⅡ型板式轨道结构的动力响应有显著影响；同时，由钢轨传至轨道板的竖向加速度明显减小，证明扣件系统对轨道竖向振动具有衰减作用。由图8～图10可知，比较转向架、车体和车轮得知，车轮的竖向加速度受线路不平顺影响更大。此外，轮轨竖向力波动区间由67.52～69.77 kN变化为 3.96～114.13 kN，波动明显。

表2 两种工况下轨道结构振动响应幅值

表3 两种工况下车辆加速度幅值 m/s2

3 结论

（1）考虑车辆与轨道的相互作用，采用更能反映结构特性与受力性状的板单元模拟轨下结构，建立了分析车辆-板式轨道耦合系统的动力分析模型及算法。该模型与算法考虑了轮轨非线性接触行为和线路随机不平顺，更接近实际，计算结果更准确、可靠。

（2）通过引入交叉迭代法求解车辆-轨道耦合系统动力学方程，提高了计算效率和精度。

（3）为了验证本文模型的正确性，计算了高速动车作用下钢轨竖向挠度曲线与轮轨力，并与文献［9］模型计算结果及其实测结果进行对比，两者波型吻合良好。

（4）仿真分析了线路平顺和不平顺工两种况下，CRH3型动车通过 CRTSⅡ板式无砟轨道时，轨道和车辆结构的动力响应。计算表明，线路不平顺对轨道结构的动力响应有较大影响，尤其是对钢轨的位移和加速度、车轮的加速度以及轮轨作用力有显著影响。

［1］ 翟婉明.车辆-轨道耦合动力学［M］.3版.北京：科学出版社，2007.

［2］ 罗文俊，张辛元.高速铁路高架桥局部振动的有限元分析［J］.噪 声 与 振 动 控 制 ，2014，34（6）：148-152.

［3］ 宋小林，翟婉明，王少林.高速铁路无砟轨道基础结构垂向位移 分 布 特 性 分 析［J］.土 木 工 程 学 报 ，2012，45（5）：162-168.

［4］ 孙璐，段雨芬，赵磊.高速铁路 CRTSⅡ型板式无砟轨道动力特 性 分 析［J］.东 南 大 学 学 报 ，2014，44（2）：406-409.

［5］ 张斌，雷晓燕.基于车辆-轨道单元的无砟轨道动力特性有限元 分 析［J］.铁 道 学 报 ，2011，33（7）：78-85.

［6］ 赫丹，向俊，曾庆元.弹性支承块式轨道在高速列车作用下的动 力 响 应 分 析［J］.中 南 大 学 学 报 ，2010，41（2）：770-775.

［7］ 雷晓燕，张斌，刘庆杰.轨道过渡段动力特性的有限元分析［J］.中 国 铁 道 科 学 ，2009，30（5）：15-21.

［8］ 吴神花，雷晓燕.交叉迭代算法求解车辆-轨道非线性耦合方程 的 收 敛 性 讨 论［J］.华 东 交 通 大 学 学 报 ，2015，32（3）：23-31.

［9］ 徐浩，张梦楠，王平.CRTSⅡ型轨道关键参数对高速车辆-轨道垂向耦合振动响应的影响［J］.铁道科学与工程学报，2014，11（4）：121-126.

Beam-Plate Model and Algorithm Based on the Elastic Foundation of Vehicle and Track Coupling

CHEN Longchuan，LEIXiaoyan

With the advantages of good stability and little deformation，the ballastless slab track is widely used in passenger dedicated lines.A lot of work have been done in the establishment of vehicle，track and vehicle-track coupling system model and algorithm by scholars worldwide，however，the existing model can not fully simulate the actual condition，further improvement is needed.In this paper，the model and algorithm for dynamic analysis of the vehicle and track coupling system is established by adopting the element plate simulating structures under the rail.stiffness according to the characters of ballastless slab track.Then，the mass and damping matrix of two kind element plates are deduced by means of finite element method.In considering the nonlinear wheel-rail contact behavior，cross iteration method is used to solve the vehicle-track coupling system dynamics equation.In random irregular conditions，the dynamic response of vehicle and track is simulated when CRH2 train passes through the CRTS II ballastless slab track.The model is proved closer to the real condition，and the calculation result is more accurate and reliable.

slab track；vehicle-track coupling system；cross iteration method；dynamic response

U213.2+4

10.16037/j.1007-869x.2017.10.004

Author′s address Railway Noise and Vibration Environment Engineering Research Center of the Ministry of Education，East China Jiaotong University，330013，Nanchang，China

*国家自然科学基金项目（51478184）；江西省优秀科技创新团队计划项目（20133BCB24007）

**雷晓燕为本文通信作者

2015-12-18）