不同倒角半径下方柱绕流的数值模拟及水动力特性研究

杜明倩, 毛海英, 李宇佳



不同倒角半径下方柱绕流的数值模拟及水动力特性研究

杜明倩1, 毛海英1, 李宇佳2

(1. 鲁东大学土木工程学院, 山东烟台 264000; 2. 中国海洋大学工程学院, 山东青岛 266100)

为了研究不同倒角半径对方柱绕流特性的影响, 采用有限体积法, 模拟了雷诺数Re为22 500、倒角半径为0.1(为方柱边长的长度)、0.2和0.3时方柱的绕流过程。方柱近壁面采用增强壁面函数, 模型采用SST–湍流模型。根据模拟结果给出了不同倒角半径下方柱的流场涡量图以及阻力系数C和升力系数C; 利用快速傅里叶变换法得到斯托罗哈数St。结果表明, 倒角半径的增加改变了方柱的分离点, 使得尾流区长度增加, 旋涡尺度减小;C和C的振动幅值呈现先减小后增大的趋势, 倒角半径为0.1和0.2时方柱受力较小, 不存在倒角时方柱受力较大, 倒角半径为0.3时方柱受力最大; 随着倒角半径的增加, 柱体截面形式越接近圆形, 斯托罗哈数逐渐增大, 漩涡脱落频率更快。

方柱绕流; 倒角半径; 升力、阻力系数; 漩涡脱落形态; 斯托罗哈数

在桥梁工程、海洋工程和土木工程等工程领域中, 柱体结构非常常见。当流体以一定速度流经柱体时, 流体会在结构后方产生规则的旋涡脱落, 即卡门涡街现象, 这种现象会影响结构的安全和稳定性。方形和圆形截面是典型的柱体截面形式, 但是工程中同样存在带有一定倒角方形截面形式的实例, 例如带有倒角的海洋石油平台的立柱、高层建筑物和桥墩等。

目前国内外对方柱的绕流过程的研究主要通过物理实验和数值模拟的方法。实验方面随着PIV(particle image velocimetry, 粒子图像测速法)和LDV(laser doppler velocimetry, 激光多普勒测速系统)等现代测量技术的应用而不断推进, 如齐鄂荣等[1]利用PIV系统对二维水平方柱绕流的旋涡特性进行了试验研究, 得到了来流雷诺数为796~9 556、不同近壁比0.2~3.0(方柱位置到壁面距离和方柱边长之比)时方柱绕流瞬时流场分布, 分析了方柱绕流流场中旋涡发展和演化规律, 比较了瞬时流场和时均流场中旋涡结构特征, 给出了不同工况下分离区长度及斯托罗哈数St与雷诺数的关系; 施鎏鎏等[2]采用时变粒子图像速度场测试技术(TR-PIV)研究了水槽中雷诺数为2 250的近壁方柱的非定常流动特性; 杨继忠等[3]利用PIV技术研究了不同流量情况下的方柱绕流流场特征, 从方柱上游、左右两侧和下游的时均流场以及方柱下游的瞬时流场四个方面对实验结果进行了分析。

随着计算机的快速发展数值模拟可以方便、有效地研究柱体绕流问题, 许多学者采用数值的方法研究方柱绕流问题。毕继红等[4]运用流体计算软件CFX, 采用层流和SST湍流模型模拟了静止方柱和圆柱在不同雷诺数条件下(层流区、亚临界区、超临界区)的绕流问题, 发现较大雷诺数时方柱的斯托罗哈数远低于圆柱的斯托罗哈数, 但同时其阻力系数却高于圆柱的阻力系数, 而在圆柱绕流中明显存在的阻力危机现象在方柱绕流中并不明显; 沈立龙等[5]基于RNG–模型对亚临界雷诺数下单圆柱和单方柱绕流进行了数值模拟, 结果表明亚临界雷诺数下圆柱和方柱绕流边界层分离点不同, 圆柱的分离点随着雷诺数的增大而逐渐向柱后方推移, 方柱的分离点则固定在柱前两个棱角位置; 李雪健等[6]采用标准–模型和DES模型对不同雷诺数下二维和三维单方柱绕流流场进行数值模拟, 发现随着雷诺数的增加, 阻力系数的平均值增加而斯托罗哈数先增大再减小的现象。

通过上述的分析, 发现物理试验和数值模拟结果都较好地反映了方柱和圆柱绕流的流动特性, 但并未见针对带有倒角的方柱绕流问题的研究。本文基于对方柱绕流机理的研究, 通过有限体积法对不同倒角半径的单方柱二维绕流流场进行数值模拟, 研究不同倒角半径对方柱绕流流场形态、升力系数、阻力系数和涡脱落频率的影响, 对方柱绕流问题的实际物理机制进行了合理的分析, 在实际工程中具有一定的借鉴意义。

1 计算模型

1.1 控制方程

假设流体为粘性不可压缩流, 即密度不变。又假设温度变化不大, 则能量方程可以忽略。故N-S方程只考虑连续方程和动量方程。

连续方程:

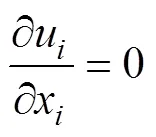
动量方程:

式中为密度,为压强,是流体运动粘性系数。

1.2 湍流模型

Menter[7]基于–湍流模型和–湍流模型, 引入Bradwhaw假设, 提出了SST–两方程湍流模型。在通常的两方程涡粘性湍流模型中,–模型能够较好地模拟远离壁面处已充分发展的湍流流动,–模型则更广泛地运用于各种压力梯度下的边界层问题。而综合了两种模型各自优势的SST–湍流模型, 在近壁面处保留了原始的–模型, 在远离壁面处应用了–模型, 这一特点使得采用SST–湍流模型来模拟绕流问题结果会更为精确。模型方程如下:

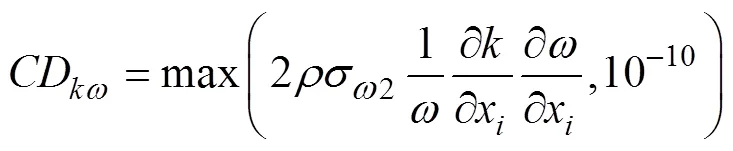
式中,表示距离壁面的距离,CD代表比耗散率输运方程中交错扩散项的正值部分, 涡粘系数定义为

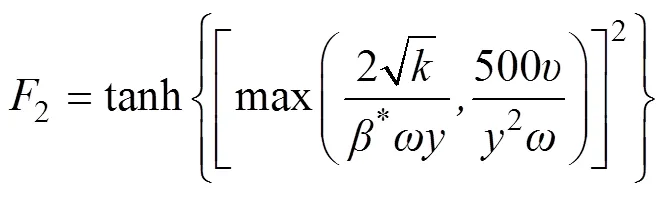
模型中常数的取值为Fluent中的默认值。

2 模型设置

2.1 计算参数

如图1, 二维计算区域为60×20, 其中为方柱边长, 方柱中心距速度入口10, 距出口边界50, 方柱直径=0.015m, 水流速度=0.39m/s。

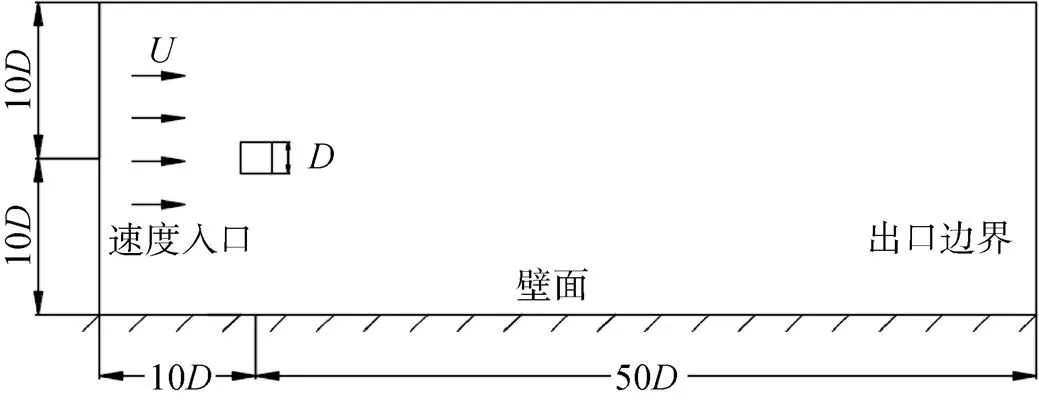
图1 计算区域和方柱布置

本文采用非结构化四边形网格, 为了精确模拟边界层处流场特征, 对方柱周围网格进行了加密处理, 方柱周围网格如图2所示。计算区域采用Fluent分离求解器进行求解, 利用有限体积法离散控制方程, 压力速度耦合采用Simple算法, 压力计算采用二阶格式, 动量用二阶迎风格式, 湍流动能和耗散率采用二阶迎风格式, 瞬态方程采用二阶隐士格式。迭代时的残差设为1.0×10–4, 时间步长取为0.002 s, 单个步长内迭代40次。

2.2 边界条件及初始条件

边界条件: 进口条件为均匀来流=1.5 m/s,=0 m/s;出口条件为自由出流; 上下边界及柱体表面为无滑移固壁边界。

图2 方柱的计算网格

初始条件: 采用瞬态模拟, 单个步长内迭代40次。

3 模型验证

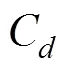
St=/(10)

式中,F为绕流阻力,为方柱的边长;为来流速度;为涡街脱落频率;为流体密度。

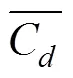
表1 单方柱绕流模拟计算结果

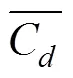
4 计算结果及分析

对Re为22 500、倒角半径分别为0.1、0.2和0.3的方柱进行数值模拟, 发现倒角半径对尾流形态、斯托罗哈数和升阻力系数有较大影响。

4.1 旋涡脱落形态

不同倒角半径下方柱绕流的尾流形态如图3所示。

图3 尾流形态图

从图3中可以看出, 在计算的所有工况中, 上下两侧壁面附近交替产生旋涡脱落, 进入尾流区与外部流动相互作用后, 向下游发展, 形成卡门涡街。方柱后的尾流区上下两侧旋涡总有一侧的尾涡占主导地位, 同时下游流场也不对称。

当存在倒角时方柱后方的尾流区会发生一定的变化, 尾流区长度增加, 旋涡数量也会增加, 但是每个旋涡能量会减小。三个不同倒角半径的单方柱绕流流场规律比较相似, 但并非完全一致。当倒角半径由小到大时, 方柱后方会产生一定的变化, 如尾流区的长度, 会随着倒角半径的增加而缩短。经过分析, 这与分离点位置的不同有很大的关系。方柱有凸出的棱角, 分离点会固定在方柱的前后两个棱角位置, 而当存在倒角时方柱的分离点不固定, 倒角半径发生变化时分离点会从角点位置向后推移, 导致流场区域发生较大变化, 旋涡脱落尾迹中的涡街数量增多, 但是每个涡街尺度变小。

4.2 升、阻力系数

Re为22 500下不同倒角半径的方柱绕流的C、升力系数C随时间变化如图4所示。

C和C是反映方柱水动力特性的重要参数, 阻力系数表征方柱沿来流方向的受力情况, 升力系数表征方柱在垂直与来流方向受到的力。从图4中可以看出, 单方柱的升力系数幅值显著大于阻力系数幅值, 此时的阻力系数主要来源于柱体表面的压力系数。当倒角半径为0.1, 0.2时,C和C幅值降低非常明显, 且C脉动非常小。当倒角半径为0.3时C和C均值大幅度地增加, 说明此时流场的脉动强度很大。

当结构受到外力时, 变化幅值较大的力更容易使结构发生疲劳破坏。根据以上分析可知, 当倒角半径为0.1和0.2方柱受力较小, 单方柱受力较大, 倒角半径为0.3时方柱受力最大, 此时结构更容易发生较大幅度的振动。

图4 不同倒角半径下方柱的升力和阻力系数

4.3 斯托罗哈数

斯托罗哈数反应的是旋涡脱落频率的大小, St的变化与旋涡脱落形态的变化相对应。由于旋涡脱落的周期和升力变化的周期相同, 因此对升力系数进行快速傅里叶变换(FFT)可以求得旋涡脱落频率, 进而得到St。

不同倒角半径下方柱绕流的St变化规律如图5所示。

图5 St图

由图5可知, 随着倒角半径的增加, 柱体的斯托罗哈数逐渐增大, 说明旋涡脱落频率更快。柱体倒角半径越大, 柱体越接近与圆柱, 这和同一雷诺数下圆柱绕流旋涡脱落频率大于方柱绕流旋涡脱落频率的结论相一致[10]。

5 结论

本文采用有限体积法对倒角半径为0.1、0.2和0.3的方柱绕流进行了数值模拟, 研究倒角半径对方柱流场、升阻力系数和斯托罗哈数的影响, 得到了如下结论:

(1) 在较高雷诺数下, 随着倒角半径的增加, 单方柱的绕流场的变化趋势相似, 但单方柱绕流存在固定分离点, 而倒角半径的增加会使方柱的分离点会不断移动, 使得绕流中形成的尾流区长度较长, 旋涡尺度相对较小。

(2) 随着倒角半径的增加方柱绕流C和C振动幅值呈现先减小后增大的趋势, 倒角半径为0.1和0.2时方柱受力较小, 单方柱较大, 倒角半径为0.3时最大。

(3) 随着倒角半径的增加, 柱体截面形状越近圆形, 斯托罗哈数越大, 旋涡脱落频率更快。

[1] 齐鄂荣, 卢炜娟, 邱兰, 等. 应用PIV系统研究横流中水平方柱绕流旋涡特征[J]. 武汉大学学报(工学版), 2007, 40(1): 18-24. Qi Erong, Lu Weijuan, Qiu Lan, et al. Research on vortices of cross flow past a horizontal square cylinder by PIV system[J]. Engineering Journal of Wuhan University, 2007, 40(1): 18-24.

[2] 施鎏鎏, 余俊, 万津津, 等. 近壁方柱绕流非定常特性的TR-PIV测量[J]. 工程热物理学报, 2009, 30(8): 1312-1314. Shi Liuliu, Yu Jun, Wan Jinjin, et al. TR-PIV measurements of the unsteady of the unsteady characteristics of the flow past a square cylinder near the wall[J]. Journal of Engineering Thermophysics, 2009, 30(8): 1312-1314.

[3] 杨继忠. 方柱绕流的PIV实验及数值研究[D]. 上海: 上海海洋大学, 2015. Yang Jizhong. Study on current around a square column ssing particle image velocimetry experiment and numerical simulation[D]. Shanghai: Shanghai Ocean University, 2015.

[4] 毕继红, 余化军, 任洪鹏. 静止方柱和圆柱绕流的二维数值分析[J]. 三峡大学学报(自然科学版), 2012, 34(1): 41-45. Bi Jihong, Yu Huajun, Ren Hongpeng. Two dimensional numerical simulation of flow over a static square cylinder and a static circular cylinder[J]. Journal of China Three Gorges University (Natural Sciences), 2012, 34(1): 41-45.

[5] 沈立龙, 刘明维, 吴林键, 等. 亚临界雷诺数下圆柱和方柱绕流数值模拟[J]. 水道港口, 2014, 35(3): 227- 233. Shen Lilong, Liu Mingwei, Wu Linjian, et al. Numerical simulation of the flow around circular and square cylinder at subcritical Reynolds numbers[J]. Journal of Waterway and Harbor, 2014, 35(3): 227-233.

[6] 李雪健. 较高雷诺数下串列方柱绕流的数值模拟[D]. 杭州: 中国计量学院, 2014. Li Xuejian. Two and three dimensional numerical sim­ulation of flow around a square cylinder[D]. Hangzhou: China Jiliang University, 2014.

[7] Menter F R. Two-equation eddy-viscosity transport turbulence model for engineering applications[J]. AIAA Journal, 1994, 32(8): 1598-1605.

[8] Norberg C. Flow around rectangular cylinders: Pressure forces and wake frequencies[J]. Journal of Wind Engineering & Industrial Aerodynamics, 1993, 49(1-3): 187-196.

[9] Lyn D A, Einav S E, Rodi W, et al. A laser-doppler velocimetry study of ensemble-averaged characteristics of turbulent near wake of a square cylinder[J]. Journal of Fluid Mechanics, 1995, 304(1): 285-319.

[10] 詹昊, 李万平, 方秦汉, 等. 不同雷诺数下圆柱绕流仿真计算[J]. 武汉理工大学学报, 2008, 30(12): 129-132. Zhan Hao, Li Wanping, Fang Qinhan, et al. Numerical simulation of the flow around a circular cylinder at varies Reynolds number[J]. Journal of Wuhan Univer sity of Technology, 2008, 30(12): 129-132.

Hydrodynamic characteristics and numerical simulation of flow around square cylinders at different filleting radii

DU Ming-qian1, MAO Hai-ying1, LI Yu-jia2

(1.College of Civil Engineering, Ludong University, Yantai 264000, China; 2.College of Engineering, Ocean University of China, Qingdao 266100, China)

To study the effect of different filleting radii on the flow characteristics around a square cylinder, in this study, we used Fluent software and the finite volume method to simulated a Reynolds number of 22 500, and applied filleting radii of 0.1, 0.2and 0.3in a square cylinder flow process. We used an enhanced wall function for the wall near the square cylinder and the SST–in our turbulence model. Based on the simulation results, we obtained the flow-field vorticity map, drag coefficient, and lift coefficient of a square cylinder with different filleting radii. We obtained the vortex shedding frequency by the fast Fourier transform method. The results show that the chamfer radius changed with an increasing separation column, with the wake length increasing and the vortex scale decreasing. We found the drag coefficient and lift coefficient amplitude to first decrease and then increase, with a square column stress radius for 0.1and smaller 0.2, and a unilateral column with a larger chamfer radius of 0.3With an increase in the fillet radius, the column section is connected with a circular form, the Strouhal number increases, and the vortex shedding frequency is faster.

flow around square cylinder; filleting radius; lift and drag coefficient; vortex shedding pattern; Strouhal

(本文编辑: 刘珊珊)

TV143

A

1000-3096(2017)07-0137-06

10.11759/hykx20161120001

2016-11-20;

2017-01-08

山东省自然科学基金(ZR2017BEE047); 鲁东大学科研基金(LB2016010)

[Natural Science Foundation of Shandong Province, No. ZR2017BEE047; Foundation Scientific Research Funds of Ludong University, No. LB2016010]

杜明倩(1986-), 女, 山东临沂人, 助教, 从事圆柱绕流研究; 毛海英(1985-), 通信作者, 女, 河南商丘人, 博士, 讲师, 从事海洋立管与土体相互作用、圆柱绕流及涡激振动研究, E-mail: maohaiying16@163.com

Nov. 20, 2016