近海海上风电场水下噪声传播模型适用性研究

章 蔚, 杨 红, 丁 骏, 吉新磊



近海海上风电场水下噪声传播模型适用性研究

章 蔚, 杨 红, 丁 骏, 吉新磊

(上海海洋大学海洋科学学院, 上海 201306)

通过现场采集近海海上风电场工程区运营期风机水下噪声和背景噪声数据, 计算了噪声信号的倍频带声压级, 功率谱级和峰值声压级, 确定了海上风电场水下噪声总声源级为148.3 dB, 以此开展近海海上风电工程风机水下噪声频域特性、功率密度谱特性等研究。在此基础上使用Kraken简正波模型和Bellhop射线模型对风电场运营期风机水下噪声在水平与垂直方向上的传播进行模拟, 模拟了噪声在不同频带内的衰减程度, 结果显示模型模拟结果在不同频率下的衰减趋势有着很大差异, 产生了明显的多途干涉现象, 通过实测数据对建立的噪声传播模型进行验证, 发现Kraken简正波模型在500 Hz以下, Bellhop射线模型在500 Hz以上适合模拟实际水下噪声传播情形, 同时海区本身背景噪声的存在会对预测的准确性产生影响。这些结论可用于进一步对近海海上风电场水下噪声传播的研究。

海上风电场; 水下噪声; 噪声传播模型

近年来, 随着地球化石资源的不断枯竭和人类日益提高的环保意识, 清洁能源更加受到人们的关注。风能是一种重要的清洁能源, 我国位于热带和亚热带季风气候区, 风力资源十分丰富, 具有大规模开发的潜力。为促进我国风电产业持续健康发展, 2012年7月国家能源局发布了《风电发展“十二五”规划》, 海上风电场越来越成为我国能源版图中的重要组成部分, 我国近海海上风电场的建设数量也在逐年增加。但是近海海上风电场可能对工程海域的生态环境带来一定的影响, 特别是施工期和运营期产生的水下噪声对海洋生物的影响。近海海上风电场运营期作为近海海上风电场整个生命周期中最长的一个阶段[1], 期间风机运转和机舱内的机械振动均产生水下噪声, 对近海海上风电场运营期产生的水下噪声及其传播衰减特性进行研究, 对于促进海洋环境和生物资源的保护具有一定重要的意义。

20世纪60年代以来, 科学技术迅速进步, 人类对海洋中声传播的研究投入了大量的精力, 提出并发展了多种水下声传播模型和实用程序。Porter等[2-3]为了解决海洋传播预报的问题, 提出了一种全新的算法, 构成Kraken简正波建模的基础。据文献[4], Tindle等给出了标准楔形模型的绝热简正波解。Porter等[4]基于BELLHOP模型, 采用高斯波束跟踪方法, 计算水平非均匀环境中的声场。李凡利等[5]用不同简正波的速度差异导致的到达时间上的不同来反演海底参数, 以获取海底相关信息。李佳讯等[6]选择Kraken模型为基础, 设计了一种海洋声场数值预报系统, 并运用该系统进行海洋声场数值模拟研究, 对目标区域典型的声场结构进行声线路径的模拟和传播损失的计算, 并且与前人结果比较, 证明模拟结果是正确的。黄建强等[7]利用射线理论建立浅海近程声传播模型, 指出该模型可以有效地模拟浅海声传播情况, 能够较好地满足浅海声传播仿真的需要。杨娟等[8]给出了利用射线理论建立的低频矢量声场模型, 表明用射线理论来预报声场,具有计算简便的特点。刘长华等[9]建议使用锚泊式海洋剖面观测浮标系统, 以获取海洋声环境及其他环境要素, 满足全方位立体的监测要求。谢骏等[10]使用Bellhop模型, 可以更高效地得出计算结果, 且发现该模型可便捷地选择接受特定角度的声线。目前相关的声传播研究大多集中在船舶噪声及海洋通信方面, 在海上风电工程噪声及传播模拟方面的研究明显较少。本文结合东黄海近海已建和拟建风电工程的噪声和声传播特性实例研究, 采用Kraken简正波模型和Bellhop射线模型相互结合的方式进行相关噪声的传播模拟分析, 讨论近海海上风电工程运营期水下噪声的传播衰减特性。

1 水下噪声传播理论

本文研究近海海上风电场风力发电机(简称风机, 下同)水下噪声及其在浅海声道中的传播衰减特性, 近海风机水下噪声源主要为风机的机械振动, 它通过风机机身传递至水中。本文侧重研究风机水下噪声从声源至较近接收点处的传播衰减特性。

浅海声道中, 海底声反射对研究浅海声场结构和声场预报具有重要影响作用, 海底声反射取决于海底地形和海底底质, 浅海海底、海面反射声和直达声间的相互作用在不同频率声强衰减图中形成复杂的干涉图案。简正波理论和射线理论是研究洋中声传播的两种主要方法, 它们是波动方程满足定解条件的解的两种表达形式, 简正波模型、射线模型、快速场模型、反射系数模型是上述理论的典型应用形式。高频时, 通常射线理论最实用; 低频时, 对风机水下噪声传播衰减简正波模型则更为适用。本文考虑到风机周边区域为浅海近场, 且海底地形变化不大等因素, 将采取简正波模型和射线模型进行数值模拟计算和研究。

1.1 Kraken简正波模型

作为经典的声场模型, Kraken简正波模型主要研究的是声场中声音信号振幅和相位的变化。Kraken简正波方法是用有限差分方法在分层海洋介质条件下对简正波方程求解, 来得到快速精确解。在简谐声源形成的稳态声场中, 假设海洋声道为柱面对称的分层介质, 简正波解为波动方程积分解的一种, 每一个简正波都单独满足波动方程和边界条件并且以各自的速度进行传播。波动方程的解可以表示为距离函数()和深度函数()的乘积, 即:

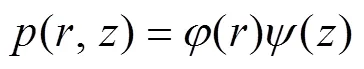
式中,为声压;为距离;为深度。Kraken模型将整个海水深度平均分为个宽度/, 于是得到+1个点, 使用有限差分近似可以将Kraken方程中的连续问题化简为标准的特征值问题。由Kraken算法得到波动方程的解为:

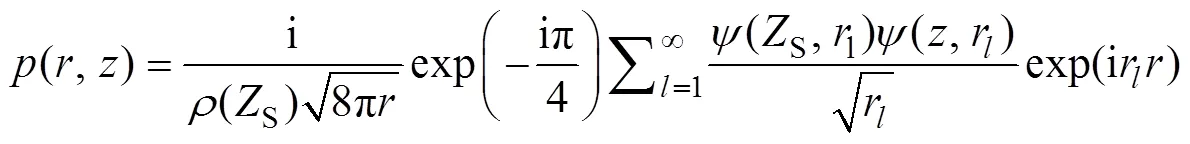
式中,为水平距离;为深度;S为源深;(S,l)为常数;为海水密度[11-12]。

1.2 Bellhop射线模型

在经典的射线理论中使用声线来表达声场中能量的传播。声线从声源出发, 经过一定的路径到达终点, 终点的声场指的是到达该点一切声线的叠加, 射线理论通过程函方程和强度方程来明确声场的路径和强度, 在分层的海水中, 射线声场的表达式为

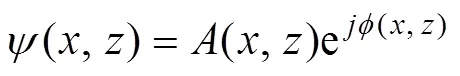
其中

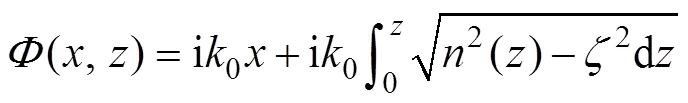
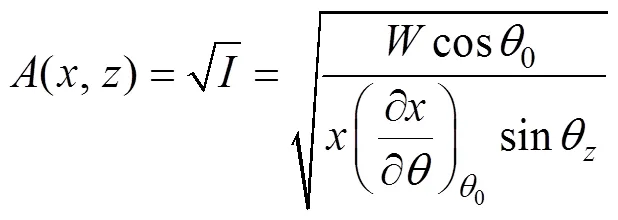
(5)式中,0为声源处声线的掠射角,为任意深度处的掠射角,是单位立体角辐射功率,()为折射率,为距离,为声线常数, 声线从1点到2点的行走时间为:

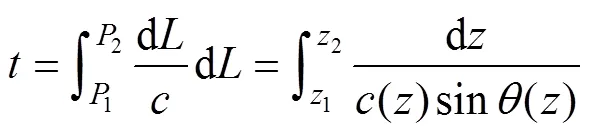
设s为出射角, 则

coss=(7)

将相位和强度与声线的路径相互结合, 来进行声压场的计算, 就可以求出声场中的传播损失[13]。

本文运用Actup v2.2L[14]软件进行声波传播模拟计算。Actup v2.2L软件一般计算过程分为以下几步: (1)建立环境文件来模拟环境, 其中包括反射系数、目标个数、目标深度、接收深度、声速剖面、频率等信息; (2)输入环境文件, 选择所需要使用的模型, 例如Kraken, 利用Kraken程序及环境文件一起生成二进制影文件, 此文件包含计算的声压场。(3)根据研究需要可以使用影文件处理得到传播衰减图等信息[15-16]。

1.3 水下噪声特性计算

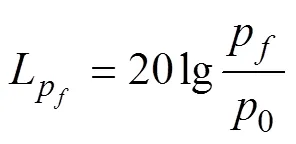
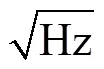
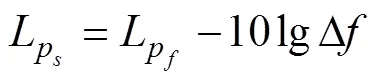
将采集的风电场水下噪声wav格式数据导入matlab, 采用pwelch程序, 通过计算输出噪声数据的声压级和声压谱级等信息[17-18]。

2 实例分析

2.1 近海海上风电场及噪声监测概况

本文选择在建的江苏盐城滨海北区风电场和已建的上海东海大桥风电场一期工程作为研究对象, 其中江苏盐城滨海北区风电场具体位置为34.38°~ 34.50°N, 120.13°~120.28°E; 上海东海大桥风电场一期工程所在位置为30.75°~30.80°N, 121.95°~122.03°E (图1)。由于两个风电场都位于水深7~13 m的浅海海域, 海域年平均风速大于7 m/s, 海底地形平坦, 沉积物多为泥砂或砂, 环境类型相似。因此可以根据上海东海大桥海上风电场一期工程运营期实测的水下噪声数据, 作为建立近海海上风电场水下噪声传播模型建模和验证依据, 同时可以应用建立的近海海上风电场水下噪声传播模型预测在建的风电场水下噪声衰减特性。

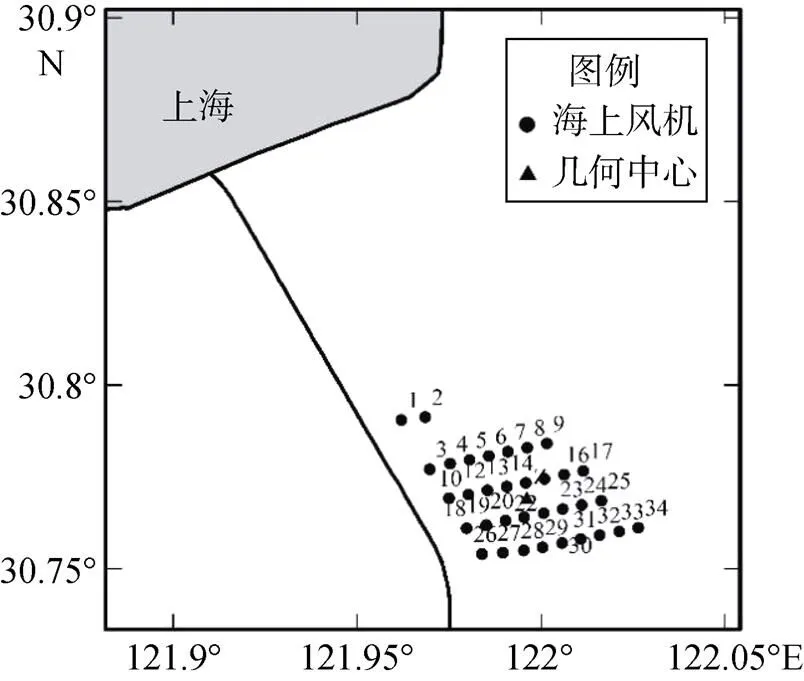
图1 东海大桥风电场位置

东海大桥海上风电场一期工程为国内首个海上风力发电项目, 一期工程共安装34台单机容量3 MW的风电机组, 编号为1—34号。本文选取的是在2014年12月23日至2015年1月4日按照GB/T5265要求对上海东海大桥风电场水下噪声采取的5次调查数据。其中(图1), 将距离东海大桥风电场2、4、8、25号目标风机3、5、10 m位置的水下噪声数据用于计算2、4、8、25号风机水下噪声的源强; 将距离25号目标风机100、200、300 m位置的水下噪声数据用于噪声传播模拟的验证数据; 将34台海上风机水下噪声源强叠加构成海上风机水下噪声源总声源级, 声源中心Z点位于34台风机的几何中心; 同时采集风机工程区的背景噪声数据。

江苏盐城滨海北区风电工程一期工程共计划安装25台单机容量4 MW的风电机组, 总装机规模为100 MW。在2014年10月23日至2014年10月24日进行了水下背景噪声数据的采集。

水下噪声数据采集过程中根据各测点具体的海域深度, 每个测点在2~6个水层深度进行测量, 每点测量记录时间均为5 min以上, 测量时船舶关闭发动机和一切发声设备并抛锚, 不产生自噪声, 同时记录测点气象水文数据。

2.2 海上风机水下噪声来源及源强确定

海上风电场风机产生水下噪声的途径有3种, 第一种是风机叶片的空气动力噪声和机舱内机械振动通过空气传入水中, 这部分噪声由于水气界面的存在, 极大地阻碍了空气噪声向水中的传播, 另外由于风机机舱高度为90 m, 在距离风机水平距离21 m以外空气噪声在水界面发生全反射, 能量无法传入水中, 因此第一种途径传入水中的噪声很微弱, 可以忽略; 第二种是机舱的机械振动噪声导致桩体的结构振动通过风机的塔筒和桩基在水中的部分传入水中, 这部分是运营期水下噪声的主要来源; 第三种途径是桩体结构振动噪声通过桩基传到海底, 再由海底辐射回水中。

在调查中对东海大桥风电场多台风机水下噪声数据进行了采集, 测量时间内主要吹东南风(SE), 风速分布在6~8 m/s (在船面2 m高度), 风机均处于正常工作状态, 由于风机场不同风机的间距均大于700 m, 且在大多数情况下, 海上风电场的整体运行噪声较接近单个风机的运行噪声[19-21], 本文选择风电场中的2、4、8、25号目标风机调查数据作为研究数据, 见图1, 在距离2、4、8、25号目标风机3、5、10 m处采集不同水层多组水下噪声数据, 综合这些数据, 根据GJB4057-2000[22]计算出2、4、8、25号目标风机的声源级分别为142.6、145.1、139.8、144.4 dB, 以及海上风电场水下噪声总声源级即声源中心Z点处声源级为148.3 dB, 图2分别给出了东海大桥风电场海上风机水下噪声总的谱源级和1/3倍频程中心频率处的谱源级。

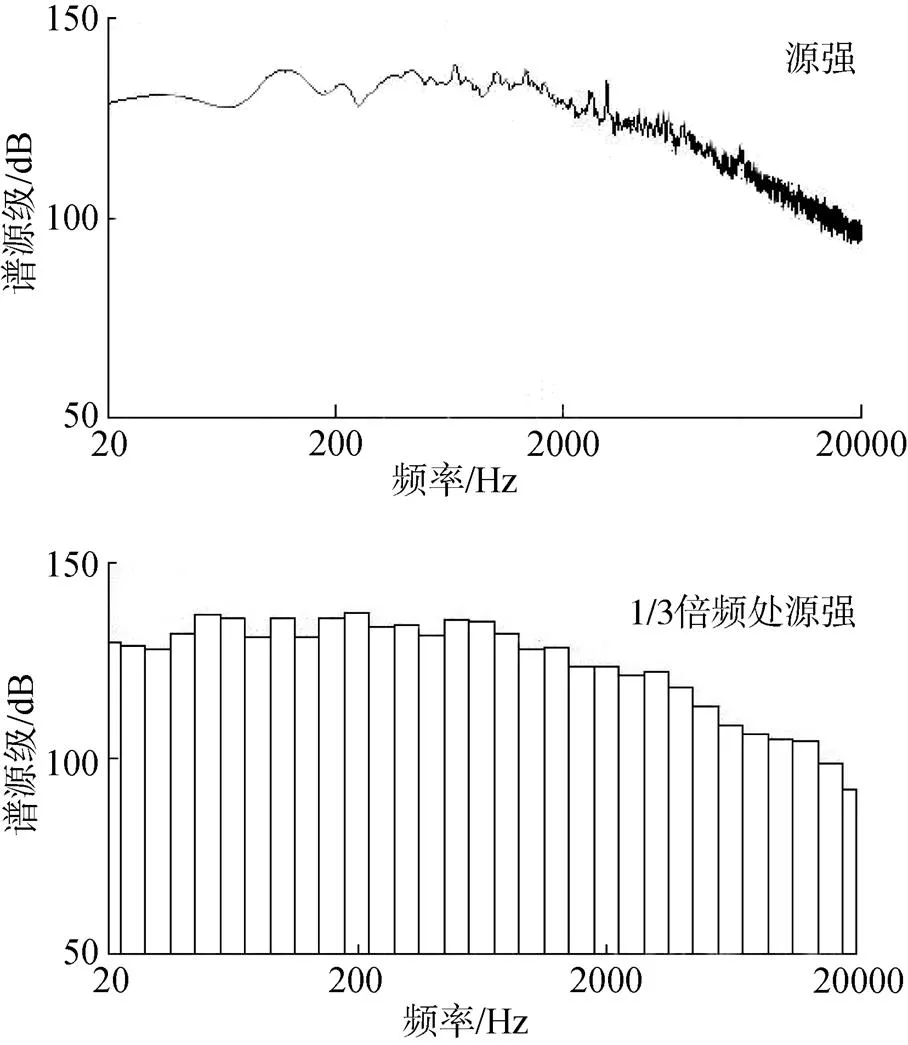
图2 风机水下噪声源强

2.3 风电场海域水下背景噪声特性分析

江苏滨海北区风电场海域环境背景噪声级随着频率的增高而下降, 在频率20 Hz~20 kHz范围内噪声谱级的总动态变化范围较大, 为40 dB, 总体上, 在100 Hz以上的声压谱级在118 dB以下; 500 Hz以上的声压谱级均在110 dB以下; 1 kHz以上的声压谱为104 dB以下; 2 kHz以上的声压谱级为103 dB以下, 5 kHz以上的声压谱级为96 dB以下。综合这些结果得出在滨海北区风电场海域环境背景噪声处于一个较高的范围, 位于90~120 dB, 峰值声压级所处1/3倍频带中心频率位于100 Hz。上海东海大桥风电场海域背景噪声同样处于一个较高的范围, 位于91~115 dB, 峰值声压级所处1/3倍频带中心频率位于125 Hz。因此在进行预测结果验证的同时要考虑背景噪声的影响, 特别是对于100 Hz左右范围。

2.4 近海海上风电场水下噪声传播模型的建立和模拟结果

1) 源强

25号目标风机的声源级为144.4 dB(re 1µPa), 通过确定的源强进行噪声传播模型的模拟预测和验证分析。

2) 频率的选择

1995年Westerburg对世界上第一个海上风电机进行测量发现噪声的峰值频率位于8 Hz和16 Hz。2000年Degn等[23]发现丹麦的Vindeby风电场和瑞典的Gotland风电场的峰值频率分别为25 Hz和160 Hz。2006年Klaus等[24]发现丹麦的Horns Rev风电场的峰值频率位于150 Hz和300 Hz, 当风机功率降低时, 峰值所处频率也随之减小了。2008年Diederichs等[25]总结了4个风电场的测量结果显示水下噪声峰值频率分别为176, 150, 135, 134 Hz。《海上风电工程环境影响评价技术规范》要求中指出: “重点预测评价中、低频(1 kHz以下), 尤其是500~800 Hz频段噪声对评价海域水下声敏感海洋鱼类尤其是石首鱼科鱼类(如大黄鱼)的影响”。从图2可以看出风机噪声谱源级中的较大值集中于100~1 000 Hz, 在这段频率之间出现数个表示单频信号的小尖峰, 单频信号是风机有规律的机械振动产生噪声的表现形式, 因此从100~ 1 000 Hz进行源强传播的模拟验证具有较高的可信度。

综合这些国内外的研究成果, 结合风机源强的特性, 海域背景噪声的特性和海洋生物的敏感频率范围, 将预测的频率范围选定为100~1 000 Hz, 选定频率100、125、160、200、250、315、400、500、630、800、1000 Hz为模拟验证的频率。

3) 环境参数的确定

提取的水深文件, 声源深度5 m, 接收深度0到15 m, 海水声速1 500 m/s, 海水密度1 000 kg/m3, 海底声速1 610 m/s[26-27], 海底密度1 900 kg/m3, 沉积层衰减系数为0.6 dB/l等参数。

4) 模拟结果

利用Actup v2.2L声学软件在matlab软件平台上运行, 可以得到近海海上风电场水下噪声Kraken简正波模型和Bellhop射线模型模拟结果。图3和图4分别表示Kraken简正波模型和Bellhop射线模型模拟的水下噪声在不同频率下水平和垂直方向上的衰减特性, 声源深度为5 m。

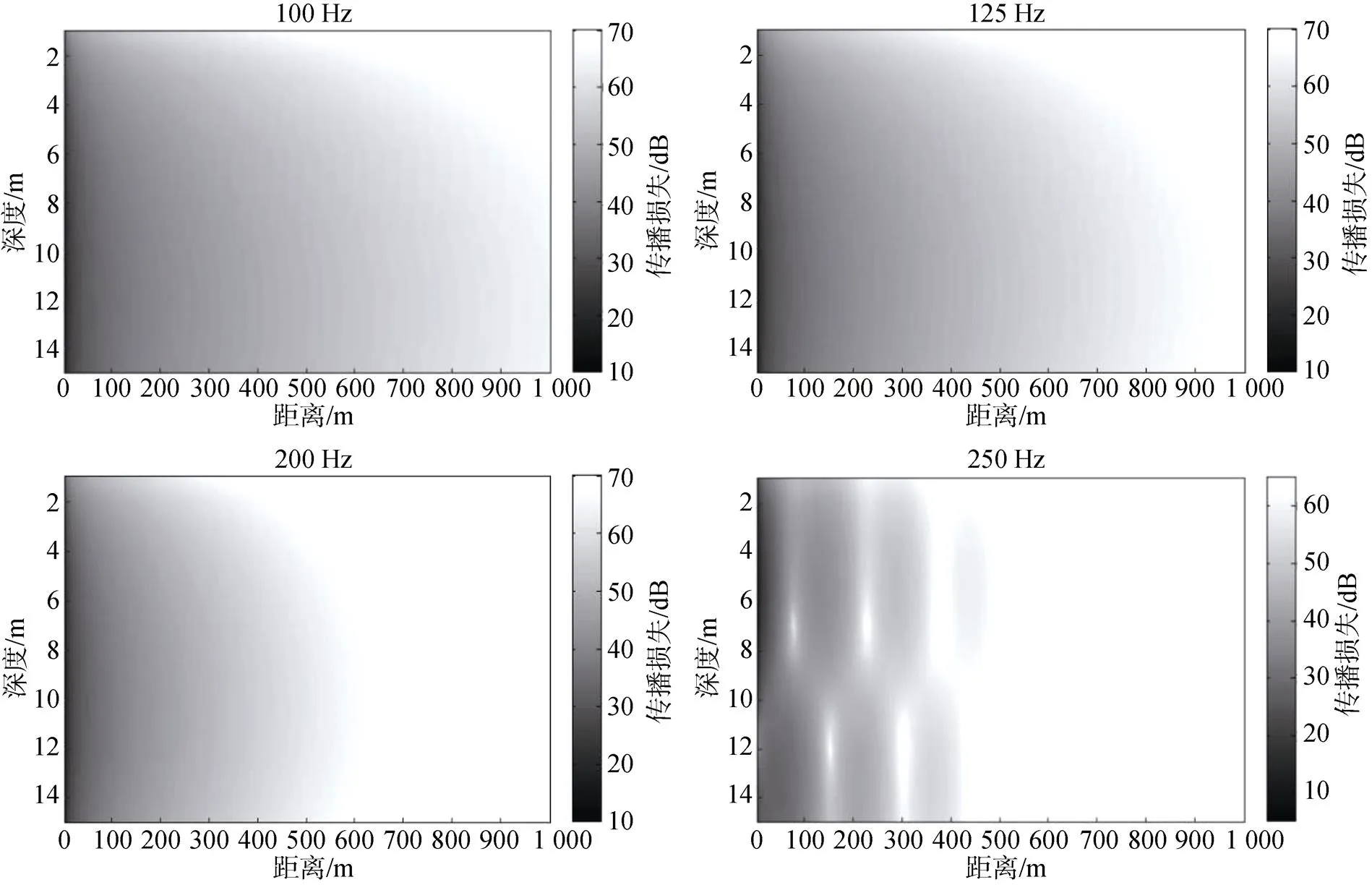
图3 Kraken模型下不同频率的衰减模拟图

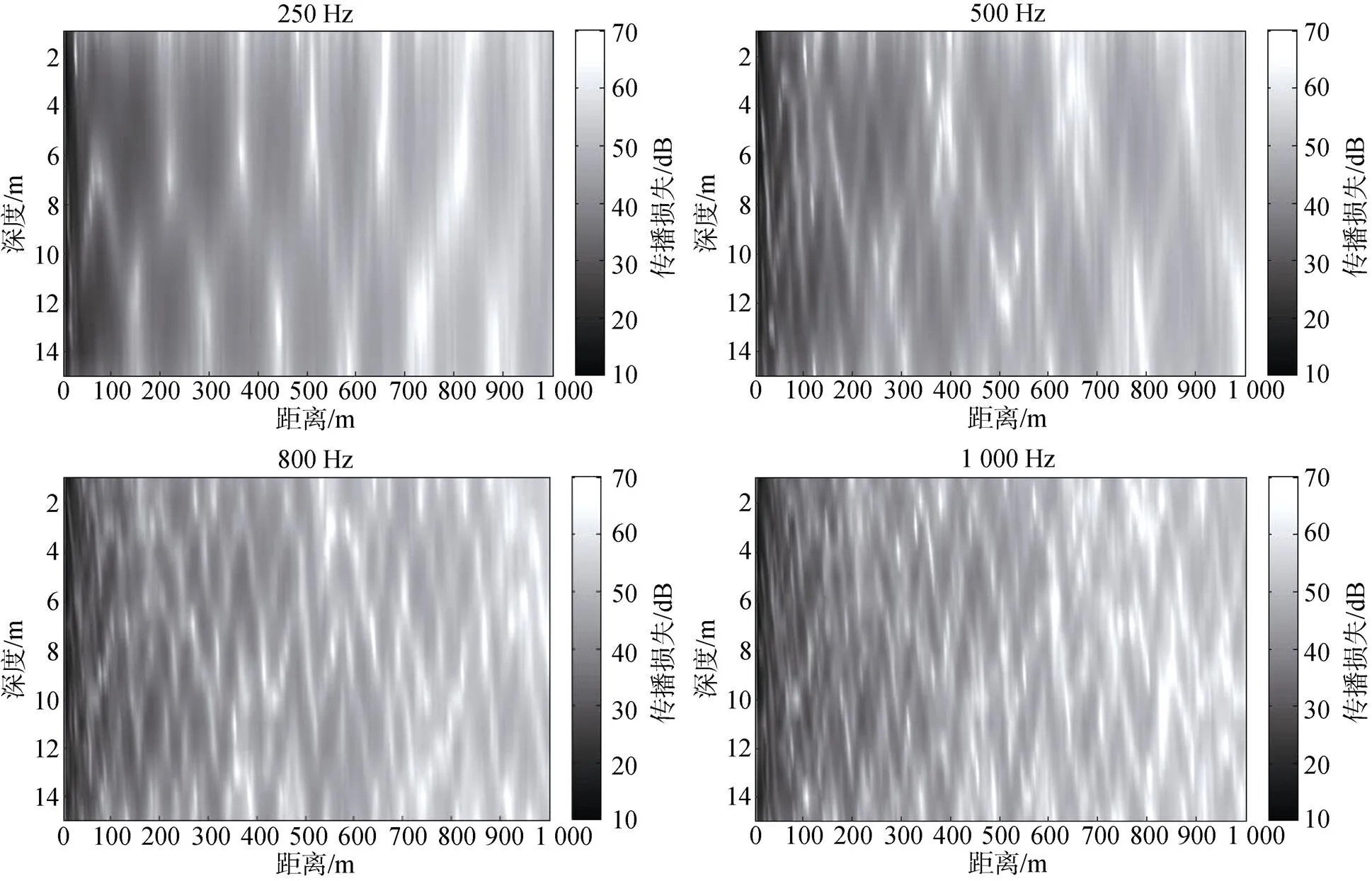
图4 Bellhop模型下不同频率的衰减模拟图

从模拟出的噪声衰减图(图3、图4)处理后可以看出噪声在水平方向和垂直方向均呈现不同程度的衰减, Kraken简正波模型和Bellhop射线模型的模拟结果在不同频率下的衰减过程有着很大的差异。Kraken简正波模型在频率100到1 000 Hz下衰减范围为20~45 dB, 在低频率下的衰减过程较为平缓, 在高频率下的衰减则变化则十分剧烈; Bellhop射线模型在频率100到1 000 Hz下衰减范围为23~53 dB, 其衰减趋势均有着很大的波动。这些剧烈的声场起伏变化表明在模拟的浅海近场环境下源强发出的声音在传播中产生了明显的多途干涉现象, 这是由于海底、海面反射, 以及直达声多途传输产生的一种效应, 会导致点声源在传播过程中受到海洋环境较大的影响, 说明模拟结果与海域实际情况有一定的一致性。

2.5 近岸海上风电场水下噪声衰减模型验证和适用性分析

现根据采集到的东海大桥风电场25号目标风机水下噪声数据做噪声传播衰减的验证, 由于风机噪声会受风机功率的变化、风力大小、潮汐变化、海况、远处船只以及东海大桥车辆的影响, 本文选用多次测量数据来真实的反映25号目标风机水下噪声的传播情况, 使用100、200、300 m三个距离上5 m接收深度的噪声数据和噪声传播模拟中5 m接收深度的模拟结果处理得出实测数据和模拟结果的对比图(图5)。从分析得出的噪声频谱图可以看出, 在100、200、300 m的水下噪声声压级数据中, 峰值声压级所处频率均为100 Hz(图5), 处于选定的范围内(100~1 000 Hz), 声压级较高的部分也基本处于此范围, 说明在模拟频率上的选择是合乎风机实际产生水下噪声情况的。风机噪声由风机的功率大小和风机本身的特性决定的, 经过计算得出25号目标风机的声源级为144.4 dB, 该结果与Klaus等[24]对丹麦的Horns Rev海上风电场水下噪声的测量结果相比大了20 dB, 推测是由于风电场风机的单机容量不同和结构差异导致, Klaus发现风机水下噪声在150 Hz处出现峰值声压级, 与本文得出的东海大桥风电场风机水下噪声在100、200、300 m处峰值声压级所处频率(100 Hz)较为接近。汪启铭[1]对福清5 MW风机运营期水下噪声中信号成分和在100、200、300 m处测量传播的衰减分析得出风机发出的水下噪声在三个距离上的衰减强度会随深度变化而变化的结论, 当深度减小, 会产生信号强度的减弱甚至成分的丢失, 汪启铭选择在水深1.5 m处和3 m处进行水下噪声的测量, 而本文是选取在水深5 m处测量的数据, 可见是较为合理的选择。

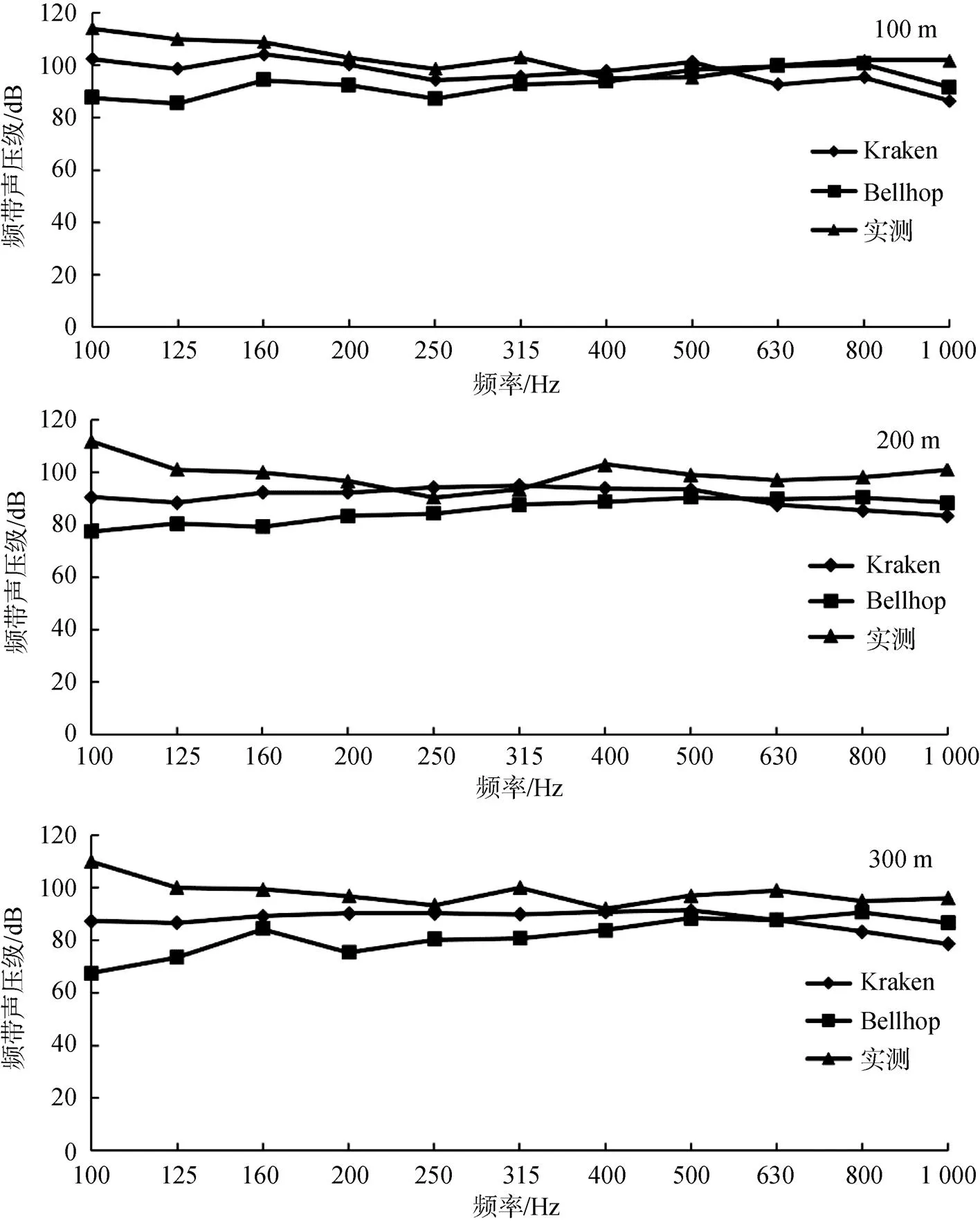
图5 三个距离上实测数据与模拟数据的对比

在距离风机100、200、300 m距离处, 使用Kraken模型进行模拟在100~500 Hz是比Bellhop模型更加接近于水下噪声传播的实际情况, 而在500~1 000 Hz, Bellhop模型是更加符合的(图5), 但是在100Hz处出现了误差达到30 dB的情况, 产生这样误差原因可能是在频率较低处受到了海洋背景噪声较大的影响, 海洋背景噪声和风机产生水下噪声叠加, 导致实测的结果较高, 也正是由于海洋背景噪声的影响, 导致了实测值在绝大多数范围内略高于模拟值。按照500 Hz以下使用Kraken模型, 500 Hz以上使用Bellhop的方法, 可以使得模拟值与真实值的误差处于10 dB以内, 可以较真实的模拟风机水下噪声的传播衰减情况。

通常情况下认为射线模型只在高频远距离下适用, 本文的结果得出在低频近场下, 射线模型同样可以发挥一定的作用, 这与杨娟等[8]的结论有较好的一致性。在海水中, 声速呈现梯度分布是一个很重要的特征, 但是由于风电场区域大多水深在10 m左右, 基本不会有声速变化, 因此在模拟中采用的是等声速梯度[28-29]。林建桓等[30]提出了结合简正波模型和射线模型提出了对远场噪声源采用简正波方法和近源采用射线方法的混合模型, 取得了很好的结果, 而本文是针对海上风电场工程, 海上风电场建设大多位于近海, 因此选取从频率高低的角度来进行具体的分析。由于海上风电场的环境相似性, 因此可以将得出的噪声传播模型适用性结果适用于滨海北区风电场和其他风电工程, 在近海海上风电场工程建设前模拟海上风电场运营期产生水下噪声的情况, 可以为风电场建设前的环境评价提供依据, 以便提出相应的预防措施, 减少水下噪声对海洋环境的污染, 对风电场海域渔业资源和珍稀海洋生物的保护做出贡献[31]。

3 结论

本文使用数据采集系统采集江苏盐城滨海北区风电场海域和上海东海大桥风电场一期工程海域水下噪声数据, 利用Matlab软件平台, 结合相关模型进行分析, 以期可以为海上风电工程中的环境保护做出贡献, 结论如下:

1) 两个风电场海域背景噪声处于一个较高的范围, 位于90~120 dB之间, 峰值声压级所处频率位于100 Hz左右, 因此在运营期的噪声模拟和验证的过程中需要考虑背景噪声的影响。

2) 根据在东海大桥风电场运营期风机附近测得的水下噪声分析计算得到2、4、8、25号目标风机的声源级分别为142.6、145.1、139.8、144.4 dB, 海上风电场水下噪声总声源级为148.3 dB, 风机声压级高的部分集中在低频范围(100~1 000 Hz), 在这段频率之间出现数个表示单频信号的小尖峰。

3) 使用Kraken简正波模型和Bellhop射线模型模拟了运营期噪声从声源至较近接收点处的传播衰减情况, 从0~300 m范围Kraken简正波模型在频率100~1 000 Hz下衰减范围为20~45 dB, Bellhop射线模型衰减范围为23~53 dB, 水下噪声在浅海近场环境传播中发生了明显的多途干涉现象, 与海域实际传播情况有一定的一致性。

4) 在500 Hz以下使用Kraken简正波模型, 500 Hz以上使用Bellhop射线模型可以较好的模拟风机实际水下噪声传播情形, 使得模拟值与真实值的误差处于10 dB以内, 发现在低频范围内出现了误差较大的现象, 可能是受到了海洋背景噪声的影响。

然而本文得出的研究成果仅仅是适用近海海上风电场运营期情形的, 近海海上风电场施工期的打桩活动也是产生水下噪声污染的一个重要环节, 打桩行为会向水下辐射高强度宽频带的脉冲式噪声, 需要进行更多的研究。

[1] 汪启铭. 海上风电场建设水下噪声对中华白海豚影响研究[D]. 厦门: 厦门大学, 2014. Wang Qiming. Research on the impact of underwater noise radiated from offshore wind farm on Chinese white dolphin()[D]. Xiamen: Xiamen University, 2014.

[2] Porter M B. The KRAKEN normal mode program[R]. Washington: Naval Research Laboratory, 1992.

[3] Porter M B, Reiss E L. A numerical method for ocean- acoustic normal modes[J]. Journal of the Acoustical Society of America, 1984, 76(1): 244-252.

[4] Porter M B, Bucker H P. Gaussian beam tracing for computing ocean acoustic field[J].Journal of the Acoustic Society of America, 1987, 82(4): 1349-1359.

[5] 李凡, 张涵, 郭圣明. 基于简正波分析的海底参数反演[J]. 声学技术, 2004, 23(z1): 68-70. Li Fan, Zhang Han, Guo Shengming. Inversion of sea-bottom parameters based on mode analysis[J]. Technical Acoustics, 2004, 23(z1): 68-70.

[6] 李佳讯, 张韧, 王彦磊, 等. Kraken海洋声学模型及其声传播与衰减的数值试验[J]. 海洋科学进展, 2009, 27(1): 51-58. Li Jiaxun, Zhang Ren, Wang Yanlei, et al. Kraken marine acoustic model and Its numerical experiment for acoustic propagation and decay[J].Advances in Marine Science, 2009, 27(1): 51-58.

[7] 黄建强, 鞠建波. 基于射线模型的浅海水声传播仿真研究[J]. 现代电子技术, 2011, 34(18): 94-96. Huang Jianqiang, Ju Jianbo. Ray model based simulation of water acoustic propagation in shallow sea[J]. Modern Electronics Technique, 2011, 34(18): 94-96.

[8] 杨娟, 惠俊英, 王德俊, 等. 低频矢量声场建模及其应用研究[J]. 声学技术, 2006, 25(1): 16-21. Yang Juan, Hui Junying, Wang Dejun, et al. Modeling and applications of vector acoustic field at low frequencies[J]. Technical Acoustics, 2006, 25(1): 16-21.

[9] 刘长华, 王春晓, 贾思洋, 等. 锚泊式海洋剖面观测浮标系统[J]. 海洋科学, 2014, 38(8): 99-102. Liu Changhua, Wang Chunxiao, Jia Siyang, et al. The system of mooring marine profiling observation buoy[J]. Marine Sciences, 2014, 38(8): 99-102.

[10] 谢骏, 笪良龙, 唐帅, 等. 基于BELLHOP模型的宽带信号波形预报[J]. 海洋科学, 2012, 36(11): 62-66. Xie Jun, Da Lianglong, Tang Shuai, et al. Broadband waveform prediction based on BELLHOP model[J]. Marine Sciences, 2012, 36(11): 62-66.

[11] 赵闪, 陈新华, 于倍, 等. 基于Kraken模型的海洋声场及相干性分析[J]. 海军工程大学学报, 2012, 24(6): 32-37. Zhao Shan, Chen Xinhua, Yu Bei, et al. Ocean acoustic filed an its coherence analysis based on Kraken model[J]. Journal of Naval University of Engineering, 2012, 24(6): 32-37.

[12] Ianniello J. A MATLAB version of the KRAKEN normal mode code[J]. Naval Undersea Warfare Center Detachment, 1994, 10(1): 94-96.

[13] Beisner H M. Numerical calculation of normal modes for underwater sound propagation[J]. Ibm Journal of Research & Development, 1974, 18(1): 53-58.

[14] Duncan A, Maggi A, Duncan A. A consistent, user friendly interface for running a variety of underwater acoustic propagation codes[J]. Proceedings of Acoustics, 2006, 20(22): 471-477.

[15] 贾浩. 海洋地声参数及声源位置的联合反演研究[D]. 合肥: 中国科学技术大学, 2009.Jia Hao. A united study of inversion for ocean geoacoustic parameters and source location[D]. Hefei: University of Science and Technology of China, 2009.

[16] Cooley J W, Tukey J W. An algorithm for machine calculation of complex Fourier series[J]. Math Comput, 1965, 19: 297-301.

[17] 薛会, 张丽, 刘以农. 非标准快速傅里叶变换算法综述[J]. CT理论与应用研究, 2010, 19(3): 33-46. Xue Hui, Zhang Li, Liu Yinong. Overview of nonuniform fast Fourier transformation[J]. CT Theory and Applications, 2010, 19(3): 33-46.

[18] 伊鑫, 曲爱华. 基于Welch算法的经典功率谱估计的Matlab分析[J]. 现代电子技术, 2010, 26(3): 7-9. Yi Xin, Qu Aihua. Matlab simulation analysis of power spectrum estimation based on welch method[J]. Modern Electronics Technique, 2010, 26(3): 7-9.

[19] Madsen P T, Wahlberg M, Tougaard J, et al. Wind turbine underwater noise and marine mammals: Implications of current knowledge and data needs[J]. Marine Ecology Progress, 2006, 309(8): 279-295.

[20] Wahlberg M, Westerberg H. Hearing in fish and their reactions to sound from offshore wind farms[J]. Marine Ecology Progress, 2005, 288(1): 295-309.

[21] Betke K, Matuschek R, Glahn S V. Underwater noise emissions from offshore wind turbines[J]. 2005, 11(1): 15-19.

[22] GJB 4057-2000, 舰船噪声测量方法[S]. GJB 4057-2000, Measurement method for noise of naval ships[S].

[23] Nedwell J, Howell D. A review of offshore windfarm related underwater noise sources[R]. UK: Subacoustech Ltd, 544R038, 2004.

[24] Betke K, Glahn S V, Matuschek R. Underwater noise emissions from offshore wind turbines[J]. Pro CFA/ DAGA, 2005, 18(2): 25-30.

[25] Blew J, Diederichs A, Grünkorn T, et al. Investigations of the bird collision risk and the responses of Harbour Porpoises in the offshore wind farms Horns Rev, North Sea, and Nysted, Baltic Sea[J]. Denmark. Status Report, 2005, 12(1): 35-37.

[26] 李艳华, 郭常升, 李会银, 等. 海底沉积物声学性质原位测量系统海上试验研究[J]. 海洋科学, 2010, 34(9): 55-59. Li Yanhua, Guo Changsheng, Li Huiyin, et al. Based on remote sensing spectral reflectance inversion of suspended sediment concentration model of surfase water at the Yellow River Estuary[J]. Marine Sciences, 2010, 34(9): 55-59.

[27] 侯正瑜, 郭常升, 王景强. 南沙海域深水区表层沉积物声速与孔隙度相关关系[J]. 海洋科学, 2013, 37(7): 77-82. Hou Zhengyu, Guo Changsheng, Wang Jingqiang. Surface sediments acoustic velocity and porosity correlation in Nansha sea area abyssal region[J]. Marine Sciences, 2013, 37(7): 77-82.

[28] 王文杰, 刘宇迪, 亓晨, 等. 南海声速跃层分类及其季节变化[J]. 海洋科学, 2014, 38(8): 82-93. Wang Wenjie, Liu Yudi, Qi Chen, et al. Classification and seasonal variability of the sound velocity spring layer in the South China Sea[J]. Marine Sciences, 2014, 38(8): 82-93.

[29] 闫庆勋, 胡建宇. 利用Argo浮标资料研究西北太平洋三维声速分布特征[J]. 海洋科学, 2013, 37(3): 22-29. Yan Qingxun, Hu Jianyu. 3-D characteristics of sound speed in the Northwestern Pacific Ocean with Argo float Data[J]. Marine Sciences, 2013, 37(3): 22-29.

[30] 林建恒, 高天赋. 简正波-射线混合风关海洋环境噪声模型[J]. 声学技术, 2003, 22(z2): 119-121. Lin Jianheng, Gao Tianfu. A hydrid wind-generated noise model of normal mode and ray[J]. Technical Acoustics, 2003, 22(z2): 119-121.

[31] Lucke K, Lepper PA, Hoeve B, et al. Perception of low-frequency acoustic signals by a harbor porpoise (in the presence of simulated offshore wind turbine noise[J]. Aquatic Mammals, 2007, 33(1): 55-68.

The applicability research of offshore wind farm underwater noise propagation model

ZHANG Wei, YANG Hong, DING Jun, JI Xin-lei

(College of Marine Sciences, Shanghai Ocean University, Shanghai 201306, China)

The noise signals of the octave band sound pressure level, the power spectrum, and the peak sound pressure level were calculated by the acquisition of the offshore wind farm project operating period and the background noise data. The underwater noise source strength of wind turbines was 148.3 dB. Studies on the frequency domain characteristics and power density spectrum characteristics of offshore wind farm engineering area underwater noise were carried out using these data. On this basis, using Kraken model and Bellhop model, the propagation of wind farm operating period underwater noise in the horizontal and vertical distance was simulated and the degree of noise attenuation in different frequency bands was predicted. It was observed that the different simulation results under different frequency attenuation trends showed a large difference and an obvious multi-approach interference phenomenon. The noise propagation models were verified by the measured data, and the adaptive frequency range of the two models was obtained (Kraken model is suitable for frequency below 500 Hz; Bellhop model can be applied to a frequency of more than 500 Hz). The presence of background noise could affect the accuracy of the prediction. These results could be used to predict the spread of the offshore wind farm underwater noise further.

offshore wind farm; underwater noise; noise propagation model

(本文编辑: 刘珊珊)

X834

A

1000-3096(2017)07-0078-09

10.11759/hykx20160423002

2016-04-23;

2016-07-25

海洋公益性行业科研专项经费项目(201205010)

[Marine Public Welfare Industry Research Special Funds Project, No. 201205010]

章蔚(1991-), 男, 安徽祁门人, 硕士研究生, 研究方向为环境海洋学, E-mail: 237429936@qq.com; 杨红, 通信作者, 女, 教授, E-mail: hyang@shou.edu.cn

Apr. 23, 2016