风电系统中变流器与蓄电池容量优化配置策略

荣飞+苏耀国+李旺

摘 要：以直驱永磁风电系统中双PWM变流器和蓄电池为研究对象，建立了以风电系统收益最大为目标的变流器与蓄电池容量优化模型，提出了基于非线性规划遗传算法的变流器与蓄电池整体容量配置策略.该策略分析了风电系统的发电收益、损失电能效益、双PWM变流器成本、蓄电池成本，建立了风电系统年收益的目标函数；同时考虑国标对风电系统并网功率波动的限制条件；并通过非线性规划遗传算法求解目标.为验证该策略的正确性，以某风电场的发电系统为仿真对象进行了分析，结果表明，相对于传统的容量配置方法，本文提出的容量优化配置策略可以使风电系统的年成本降低10.3%.

关键字：系统整体容量优化；蓄电池；风力发电系统；非线性规划遗传算法

中图分类号：TM61 文献标志码：A

A Capacity Optimal Allocation Strategy of Converters and Batteriesfor Wind Power System

RONG Fei1 ，SU Yaoguo2，LI Wang1

（1. National Engineering Research Center of Energy Conversion and Control，Hunan University，Changsha 410082，China；

2. State Grid Shanxi Province Power Company Development Planning Department，Xian 710048，China）

Abstract：This paper focused on the dual PWM converter and battery of the direct drive permanent magnet wind power generation system. In order to obtain the maximum benefit of wind power system，a capacity optimization model of converter and battery was established. The overall capacity optimization strategy of dual PWM converter and battery was proposed based on nonlinear programming genetic algorithm. The strategy analyzes the benefits of wind power system，the loss energy efficiency，and the costs of dual PWM converters and batteries. An objective function considering national restrictions on the fluctuation of output power of wind field was then established and solved by a nonlinear programming genetic algorithm，which aims at the maximum annual income of wind power system. To verify this strategy，a wind power system was emulated. The results show that，compared with the traditional capacity allocation method，the annual costs of wind power system can be reduced by 10.3%.

Key words：capacity optimization； battery； wind power generation system； nonlinear programming genetic algorithm

近年來，随着能源危机及环境问题的日益突出，风力发电技术成为新能源领域关注的焦点.然而，由于风能输入的不确定性，导致风电系统的输出功率具有不稳定性和间歇性[1-3]，难以完全满足并网要求.为了平抑风电系统并网功率的随机波动，改善系统并网电能质量，需要在系统中配置储能装置[4-5].

目前，蓄电池组成的单一储能系统和蓄电池结合其他装置组成的混合储能系统是风电储能装置的主要研究方向之一.文献[6]分析了风电场中由单一蓄电池组成的大规模储能系统的充放电控制策略，建立了基于蓄电池成本及平抑风电系统功率波动效果为目标的优化模型，并结合二次规划算法，利用Matlab实现对整个风电场的整体储能系统的蓄电池数量及容量的优化；文献[7]通过分析组合蓄能的独立式风电系统的电能传输过程，提出了针对系统中蓄电池组合电解水制氢混合储能装置的完整系统配置设计方法及能量优化管理策略，进一步优化了带储能装置的风电系统的运行过程，提高了系统的效率；文献[8]结合超级电容剩余容量的超前控制策略，以二阶低通滤波方式分析了风电系统中蓄电池与超级电容器组合的混合储能装置的功率流动过程，建立了混合储能装置年最小成本的经济评价模型，并采用粒子群算法求解优化了混合储能装置的容量配置.以上文献对风电系统中储能装置的容量优化都做了深入的研究，但只涉及储能单方面的容量优化，均未考虑其他装置，对风电系统整体进行优化.为了更加全面地分析风电系统各组成部分的容量配置，本文将以蓄电池储能的直驱永磁风力发电系统为研究对象，综合考虑系统机侧变流器、网侧变流器及蓄电池的容量，进行整体优化配置，使系统充分利用风能，降低成本，实现效益最大化.endprint

1 风电系统模型分析

1.1 风电系统拓扑

基于蓄电池储能的永磁直驱风电系统拓扑结构图如图1所示.该系统主要由风力机、永磁同步发电机（Permanent Magnet Synchronous Generator，PMSG）、机侧变流器VSC1、网侧变流器VSC2和蓄电池储能系统（Battery System，BS）构成.风力机吸收风能并转化为机械能，带动发电机发电，发电机输出的电能经过VSC1整流、VSC2逆变之后送入电网，蓄电池储能系统并联在双PWM变流器的直流母线上.系统运行过程中，若风速持续过大，风力机输入瞬时功率大于系统设定的并网功率 [9]时，则将多出部分的功率存储到蓄电池中；反之，风力机输入瞬时功率小于设定的并网功率时，则由蓄电池放电补充不足的功率，保证系统并网功率在国标允许范围内波动.

1.2 风电系统功率流分析

基于蓄电池储能的风电系统功率流动示意图如图2所示.风力机在不弃风的情况下吸收的功率为P0，由于发电机及机侧变流器VSC1的功率限制，系统不能将全部P0吸收，会损失一部分功率Ploss.风电系统将吸收的部分風能转变为电功率，流经机侧变流器VSC1输出P1.

1）当P1 > P20时（P20为VSC2的额定功率）：

为防止VSC2超负荷运行，需要将P1的一部分P3作为蓄电池的充电功率，此时P3为正.

2）当P1 ≤ P20时：

因为国标GB/T 15945-2008对风电场输出功率做出了具体的规定，如表1所示，即风电系统并网功率短时间内不能变化过大，防止对电网产生冲击.

风电场装机容量/MW10 min内最大有功功率变化限值ΔP10min/MW 1 min内最大有功功率变化限值ΔP1min/MW

<30103

30～150装机容量/3装机容量/10

>1505015

以表1所示的1 min内系统并网功率波动限制为例，假设当前时刻的前1 min内VSC1输出功率P1的最小值为P1min，最大值为P1max，则当前时刻VSC2允许输出功率的范围为[P1max-ΔP1min，P1min+ΔP1min]；

a）若P1（t） > P1min + ΔP1min：

此时，需要向蓄电池充电，系统并网功率P2（t），蓄电池充电功率P3（t）分别为：

P2（t）=P1min+ΔP1min

P3（t）=P1（t）-（P1min+Δp1min）（1）

b）若P1（t） < P1max - ΔP1min：

此时，需要蓄电池放电，使P2满足要求，系统并网功率P2（t），蓄电池充电功率P3（t）分别为：

P2（t）=P1max+ΔP1max

P3（t）=P1（t）-（P1max+Δp1max）（2）

此时P3（t）为负值，表示蓄电池处于放电状态.

对于表1所示的10 min内系统并网功率波动限制的分析类似.

1.3 系统变流器与蓄电池容量配置

以上分析是假设蓄电池容量充分大的条件下进行的，不符合工程实际情况.需要给蓄电池充电时若剩余容量不足，则必须对风力机进行变桨操作，弃掉一部分风能；需要蓄电池放电馈能时，若其容量较小，则可能出现蓄电池无法提供足够放电功率，导致系统并网功率波动越限.

因此，为了防止并网功率波动越限，必须尽可能增大蓄电池的容量，但随容量的增大，其成本会急剧上升，所以需要综合考虑，合理地配置蓄电池的容量.

对于变流器VSC1的额定功率，为了使风电系统充分吸收风能，需要尽可能增大P10，但会带来成本的增加，因此，本文考虑优化VSC1的容量配置，以兼顾VSC1的成本和效率.

对于网侧变流器VSC2，其额定功率一般配置为与VSC1的额定功率相等[10].但工程中，考虑到VSC1需要对蓄电池充电，所以，VSC2的额定功率可小于VSC1的额定功率，然而VSC2的额定功率过小又使得风电系统馈入电网的功率下降，因此必须合理设计.

基于以上分析，本文提出一种直驱永磁风电系统的变流与储能装置整体容量优化配置策略，使系统年收益最大.

2 优化模型建立

2.1 目标函数

风电系统变流器和蓄电池容量优化配置的目的是使风电系统年收益J0最大，目标函数定义为：

J0=Max{Pgrid-Ct}（3）

式中： Pgrid为风电系统一年的上网电能产生的经济收益； Ct为风电系统的年投资成本.已知：

Pgrid=Pt-Closs（4）

式中：Pt为风机在不弃风情况下一年吸收的风能总量产生的经济收益，Pt为常数；Closs为风电系统一年内损失的风能可以产生的经济收益，故目标函数转化为J：

J=Min{Ke×Wloss+（Kp+Kg）×P10+kp2×

P20+Kp3×S30}（5）

式中：Ke为每度电的上网电价；Wloss为风电系统年损失电能；Kg，Kp，Kp2，Kp3分别为发电机、VSC1，VSC2和蓄电池的单位容量的年投资成本.

风电系统的年损失风能Wloss为：

Wloss=∫x0[P0（t）-P1（t）]dt（6）

式中：积分上限x表示1年的总控制周期数，以控制周期1 s为例，则x取值为31 536 000.

2.2 约束条件

风力机吸收的风功率P0可看成是已知量.因为流过变流器的功率P1，P2 不能超过其对应的额定功率P10，P20，故P1，P2必须满足如下条件：endprint

0≤P1（t）≤P10

0≤P2（t）≤P20

P20≤P10（7）

式中： P20≤ P10是为避免造成VSC2容量浪费、节省变流器成本而设置.根据表1所述的国标要求，即 1 min内风电系统的并网功率P2的波动不超过ΔP1 min，10 min内P2的波动不超过ΔP10 min，所以有：

Max[P2（0∶60）]-Min[P2（0∶60）]≤ΔP1 min

Max[P2（0∶600）]-Min[P2（0∶600）]≤ΔP10 min（8）

蓄电池的充电功率P3与它在t时刻的实时储能S3（t）满足一定关系，且任意时刻蓄电池的实时储能必须小于或等于其额定容量，所以有：

P3（t）=P1（t）-P2（t）

S3（t）=S3（0）+∫t0P3（t）dt

0≤S3（t）≤S30（9）

式中：S3（0）表示蓄电池的初始储能，且蓄电池充电时，其剩余容量必须满足以P3大小的功率充电1 s；蓄电池放电时，其储存的电能足够以P3大小的功率放电1 s，具体如式（10）所示：

P3（t）ΔT≤S30-S3（t），P3（t）≥0；

-P3（t）ΔT≤S3（t），P3（t）<0.（10）

2.3 非线性规划遗传算法

本文提出的优化模型是一个多变量目标函数，且各变量存在上述诸多约束条件，同时计算处理的数据量大，耗时长，为快速求解目标函数全局最优解，本文采用非线性规划遗传算法[11]，具体步骤为：

1）种群初始化.由系统随机产生m个n位二进制数构成算法的初始种群；种群中每个个体基因前i位代表P10，中间i位代表 P20，最后j位代表S30； n = 2i+j.

2）个体适应度计算.

a）基因解码：取种群个体基因3个位段的二进制数换算成十进制数，即获得该个体对应的P10，P20，S30，然后计算得到Wloss.

b）约束条件限制：利用上述约束条件判断每个个体的P10，P20，S30是否满足条件，保留符合条件的个体，忽略不满足要求的个体并重新由系统随机产生同等数量的个体、解码、判断，若仍存在不符合条件的个体，则重复该步骤，直至种群m个个体全部满足约束条件.

c）计算个体适应度：根据个体的P10，P20，S30，Wloss，利用式（3）计算出个体的目标函数值，保留每一代种群中目标函数值最小的个体.

3）选择、交叉、变异.本文采用轮盘赌算法对个体进行选择，为下一代种群的产生做准备.轮盘赌算法保证了目标函数值较小的个体以较大的概率被选中遗传至下一代，有助于加快目标的收敛速度.

个体之间的交叉即以概率pc决定相邻两个体之间是否交叉，并随机选择个体的某几位进行互换.

个体变异即以概率pm决定是否进行变异并对需要变异的个体随机选择某一位进行0—1置换.

个体经过选择、交叉、变异即产生新一代种群.

4）终止判断条件.如果连续4代种群中最小目标函数值变化均小于一个较小的值ε，则表明目标收敛，结束算法，以最后一代种群中最小目标函数值对应个体解码所得的P10，P20，S30为优化结果；否则，轉入步骤2）.

3 算例分析

3.1 容量优化仿真结果

本文以江苏盐城某风电场的风力资源为原始数据进行算例分析.由于用全年的风能数据进行计算，计算量过大，为验证本文提出的容量优化配置方法，本算例只取该风电场一年中某典型日的风能数据进行计算，并以此结果为依据计算出J.

已知风电场某典型日高于地面90 m的风功率P0如图3所示，数据采样时间间隔为1 s，通过计算可知风电系统日输入风能W0为74.285 MW·h.

已知风电系统中发电机年投资成本Kg=400元/kW，机侧变流器、网侧变流器的年投资成本均为200元/kW，蓄电池单位容量的年投资成本Kp3=400元/kW·h及上网风电价格Ke=0.53元/kW·h.

非线性规划遗传算法参数给定如下：初始种群个体数m=60，P10，P20的基因位数i=15，S30的基因位数 j=13，个体交叉概率pc=0.6，个体变异概率pm=0.1，算法终止条件ε=0. 1.

结合以上参数，采用Simulink搭建风电系统仿真模型，获得满足约束条件的相关参数，然后通过Matlab编程计算获得目标函数各变量的收敛波形，如图4所示.本算例中J = KP1×P10 + KP2×P20 +KP3×S30+Ke×Wloss×365，其中，Wloss为风电系统日损失风能.

图4（a）为风电系统年成本J的收敛波形，由图可知，经过45次进化，J最终收敛于902.1万元.图4（b）为风电系统机侧变流器VSC1的额定功率P10的收敛波形，最终收敛于10.425 MW.图4（c）为风电系统网侧变流器VSC2的额定功率P20的收敛波形，最终收敛于9.527 MW.图4（d）为风电系统的蓄电池额定容量S30的收敛波形，最终收敛于0.999 MW·h.图4（e）为风电机组日损失风能Wloss的收敛波形，最终收敛于1.971 MW·h.

出现上述结果的原因如下：

1）VSC1，VSC2的单位容量成本较低，蓄电池的单位容量成本较高，当P10，P20取很小的值而S30取很大的值时会导致J很大.

2）P10，P20很小时会使风电机组损失更多的风能而增大Wloss，进一步导致J很大；因此，随着P10，P20的增大和S30的减小，Wloss会减小并最终趋于稳定.

将P10，P20，S30及图4所示的风功率数据代入系统仿真模型中，即可获得风电系统并网功率P2，蓄电池的充电功率P3以及风电系统的损失功率Ploss的波形分别如图5（a），5（b），5endprint

3.2 经验配置仿真结果

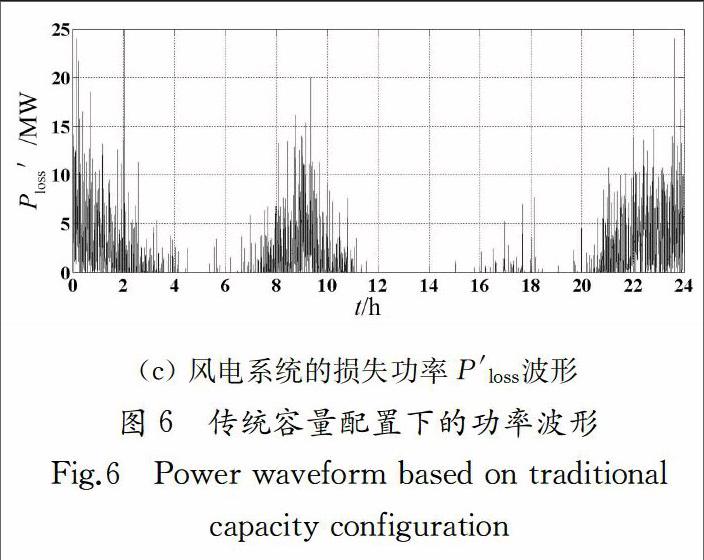
根据与某风电厂家多年合作的工程经验可知，系统中机侧变流器VSC1的额定功率取值为风力机输入功率P0的平均值的1.2倍，网侧变流器VSC2的额定功率取值与VSC1的额定功率相同，即P10′= P20′=5.224 MW，蓄电池容量配置为1 h内VSC1按额定功率输出的能量值，即S30′=5.224 MW·h.将P10′， P20′， S30′及图3所示的风功率数据导入风电系统的仿真模型中，即可获得经验配置方法下风电系统并网功率P′2、蓄电池的充电功率P′3以及风电系统的损失功率P′loss的波形，如图6（a），6（b），6（c）所示.

3.3 对比分析

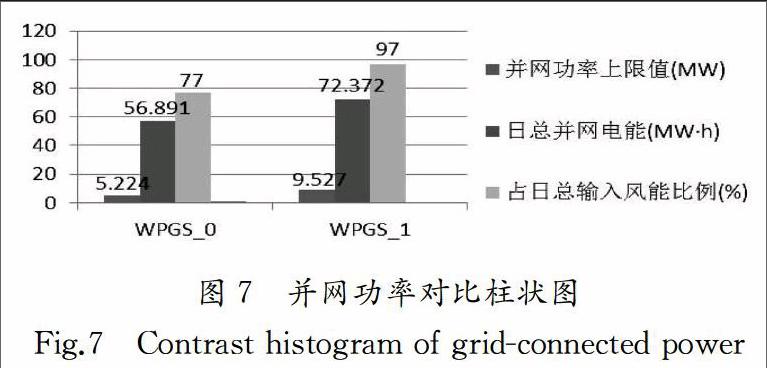
通过对上述两种方法的并网功率波形进行分析计算可得图7所示的柱状图，其中，WPGS_0表示基于经验方法的并网功率柱状图，WPGS_1表示基于NPGA的并网功率柱状图.由图可知，WPGS_1的并网功率上限为9.527 MW，是WPGS_0的近2倍；同时，WPGS_1的并网风能比WPGS_0高15481 MW·h，其日并网电能占日输入风能的97%，比WPGS_0多出20%，几乎将风能全部转换并网，风能利用率得到显著提高.

对风电系统充放电功率波形进行分析计算可得图8所示的柱状图.从图中可看出，WPGS_1的蓄电池充放电时间比WPGS_0的长，充放电功率大，利用率高，可减少其剩余容量的闲置.

对两风电系统损失功率波形进行分析计算可得图9所示柱状图.由图可知，WPGS_0损失功率大、风能利用率低；WPGS_1损失功率小，风能利用率高，只占总输入风能的3%，这是优化算法使蓄电池得到了充分利用的结果.

图10为风电系统容量配置及成本对比柱状图.由图可知，WPGS_1的VSC1，VSC2额定容量比WPGS_0大近两倍，蓄电池额定容量相对小很多，这是由于蓄电池单价较高、变流器单价较低导致的.因此，NPGA配置出总成本最低的装置容量必然使VSC1，VSC2容量小而蓄电池容量大.

由图10（b）可知，尽管WPGS_0的VSC1，VSC2配置较大使其装置成本大于WPGS_0，但年成本仍小于WPGS_0，经计算可知，WPGS_1的年成本较WPGS_0少103.6万元，减少约10.3% .

4 结 论

本文提出的基于风电系统并网功率波动限制及系统效率的蓄电池与双PWM变流器整体容量优化配置策略不仅能保证蓄电池充放电平衡、风电系统正常运行及系统并网功率满足国标要求，而且实现了系统年收益最大化.仿真结果表明：相对于经验配置方法，采用本文的方法能使风电系统充分利用风能，减少浪费，大幅度提高其发电效率，增加收益.

参考文献

[1] 孙承晨，袁越，CHOI S S，等.用于能量调度的风–储混合系统运行策略及容量优化[J].电网技术2015，39（8）：2107-2114.

SUN Chengchen，YUAN Yue，CHOI S S，et al.Capacity optimization and operational strategy of the wind-energy storage hybrid systems for energy dispatching[J].Power System Technology，2015，39（8）：2107-2114.（In Chinese）

[2] 楊欢，赵荣祥，辛焕海，等.海岛电网发展现状与研究动态[J].电工技术学报，2013，28（11）：95-105.

YANG Huan，ZHAO Rongxiang，XIN Huanhai，et al.Development and research status of island power systems[J].Transactions of China Electrotechnical Society，2013，28（11）：95-105.（In Chinese）

[3] ESMAILI A，NOVAKOVIC B，NASIRI A，et al.A hybrid system of Li-Ion capacitors and flow battery for dynamic wind energy support[J].IEEE Transactions on Industry Applications，2013，49（4）：1649-1657.

[4] JIANG Q，HONG H. Wavelet-based capacity configuration and coordinated control of hybrid energy storage system for smoothing out wind power fluctuations[J].IEEE Transactions on Power Systems，2013，28（2）：1363-1372.

[5] 丁明，徐宁舟，毕锐.用于平抑可再生能源功率波动的储能电站建模及评价[J].电力系统自动化，2011，35（2）：66-72.

DING Ming，XU Ningzhou，BI Rui.Modeling of BESS for smoothing renewable energy output fluctuations[J].Automation of Electric Power System，2011，35（2）：66-72.（In Chinese）

[6] SAVKIN A V，KHALID M，AGELIDIS V G. Optimal size of battery energy storage and monotonic charging/discharging strategies for wind farms[C]//2014 IEEE Conference on Control Applications.Juan Les Antibes：IEEE，2014：1372-1376.endprint

[7] 卢闻州，周克亮，程明，等.组合蓄能独立式风力发电系统[J] .电工技术学报，2011，26（2）：165-172.

LU Wenzhou，ZHOU Keliang，CHENG Ming，et al.Stand-alone wind generation system with hybrid energy storage[J] .Transactions of China Electrotechnical Society，2011，26（2）：165-172.（In Chinese）

[8] 王博堃，滕欢，胡晓通，等.基于平滑控制策略的混合储能优化配置方法[J].高压电器，2015（10）：47-53.

WANG Bokun，TENG Huan，HU Xiaotong，et al.Hybird energy storage system optimal configuration based on smooth control strategy[J].High Voltage Apparatus，2015（10）：47-53.（In Chinese）

[9] 戴慧珠，遲永宁.国内外风电并网标准比较研究 [J].中国电力，2012，45（10）：1-6，11.

DAI Huizhu，CHI Yongning.Comparative study on wind power grid connected standards at home and abroad [J].Electric Power，2012，45（10）：1-6，11.（In Chinese）

[10]马伟明，肖飞.风力发电变流器发展现状与展望 [J].中国工程科学，2011，13（1）：11-20.

MA Weiming，XIAO Fei.Development status and prospect of wind power converter [J].Engineering Sciences，2011，13（1）： 11-20.（In Chinese）

[11]AMERI A A，NICHITA C，RIOUCH T，et al.Genetic algor-ithm for optimal sizing and location of multiple distributed generations in electrical network[C]//2015 Modern Electric Power Systems （MEPS）.Wroclaw，2015：1-7.endprint