基于可靠性的结构动态拓扑优化方法

唐东峰+游世辉

摘 要：实际工程结构设计往往在确定性范畴内进行，所得结构存在较大失效可能性.基于此，提出一种基于可靠性的连续体动态拓扑优化方法，将结构可靠性分析方法嵌套到连续体拓扑优化中.考虑了结构几何尺寸和材料体积的不确定性，并用高斯分布来度量.将结构可靠度作为约束嵌套到连续体拓扑优化中，属于二次嵌套优化问题，但计算效率低下，不适于工程应用.提出一种解耦策略将结构可靠性分析从连续体拓扑优化中解耦出来，使结构可靠性分析与动态拓扑优化为两个独立的优化循环，大大提高了计算效率.建立以结构基频最大为优化目标，满足一定体积约束和可靠度要求的优化问题，利用各向同性材料惩罚模型（SIMP）和移动渐进方法（MMA）求解该优化问题.所提方法可以得到满足不同可靠度要求的一系列最优结构，并用标准算例验证其有效性.

关键字：可靠性；不确定性；动态拓扑优化；解耦

中图分类号：TM30 文献标志码：A

Reliability-based Structural Dynamic Topology Optimization Method

TANG Dongfeng1，2，YOU Shihui1

（1.College of Civil Engineering and Mechanics，Xiangtan University，Xiangtan 411105，China；

2. School of Information and Electrical Engineering，Hunan University of Science and Technology，Xiangtan 411201，China ）

Abstract：Actual engineering structures are often designed using deterministic parameters，which may lead to high failure probability. This paper proposed a reliability-based structural dynamic topology method，in which structural reliability analysis was incorporated into the topology optimization procedure. The geometry dimensions and material volume were considered as uncertain parameters，and it was assumed that they obey a Gaussian distribution. It is a two-nested optimization problem when the structural reliability analysis is considered as constraints into the topology optimization，which results in low efficiency and cannot be used in practice. To this end，a new decouple strategy was proposed to decouple the reliability analysis from the topology optimization procedure. In this case，structure reliability analysis and dynamic topology optimization become two independent optimization cycles，and the computational efficiency is improved enormously. The design problem was then constructed so as to maximize the first eigenfrequency and to meet the volume and reliability requirement. SIMP and MMA were combined to successfully solve the design problem. The proposed method can produce various topologies that satisfy different reliability requirement，and its validity is demonstrated by one benchmark example.

Key words：reliability； uncertainty； dynamic topology optimization； decouple

連续体拓扑优化方法旨在满足一定约束条件下寻求材料最优分布，相对于尺寸优化[1]和形状优化[2]，它有更多的设计自由度，同时也是更具挑战性的研究领域.自从1988年Bendse和Kikuchi[3]提出基于均匀化法的结构拓扑优化理论以来，连续体拓扑优化方法[4-10]经过近30年的发展，已经成功应用到各种领域，如航天[11]、碰撞[12]、汽车[13]和桥梁[14]等.其中，动态连续体拓扑优化问题[15-17]更具有挑战性，其难点在于优化过程中需要克服局部模态和频率交换现象，研究相对较少.

尽管传统连续拓扑优化方法可以得到性能优越的设计结果，但是，其未考虑结构参数的不确定性.不确定性是工程结构的固有属性，在结构设计时不容忽略，否则设计出的产品会存在较大的失效风险，甚至可能造成灾难性的后果[18-19].考虑结构不确定性的优化设计方法一般分为两类：稳健性优化设计方法[20]和基于可靠性优化设计方法[21].前者为了降低不确定性变量对结构响应的敏感性，而后者使结构优化设计增加一个可靠度约束.基于可靠性的优化设计方法可以得到满足设计人员一系列不同可靠度要求的结构.而基于可靠性的连续体拓扑优化方法的研究，由于其设计变量数量庞大，且功能函数往往为隐式，更具有挑战性.Kharmanda等[22]首次将结构可靠性分析引入到连续体拓扑优化中，研究发现所提方法设计出的结构比传统确定性方法所得结构更加可靠.在其研究基础上，该领域越来越受到国内外学者的关注，出现大量研究成果[23-27].最近，Zhao等[28]提出一种高效的基于可靠性连续体拓扑优化方法，利用随机响应面显式表达结构失效功能函数.Liu等[29]结合一次二阶矩法和描述函数拓扑优化方法探讨了一种可以获得光滑边界且满足一定可靠度要求的优化方法.Jalalpour和Tootkaboni[30]考虑材料的不确定性，提出了一种高效的基于可靠性的连续体拓扑优化方法，假设材料服从相关对数正态分布，并利用随机摄动法近似得到结构响应，使结构功能函数近似显式化.endprint

然而，上述研究均是静力学方面的研究，动力学方面的研究甚少.动态拓扑优化问题研究本身就较静力学拓扑优化繁琐，将可靠性分析与动态拓扑优化相结合更加具有挑战性.工程中存在大量承受动载荷的结构，这些结构较之静力下的结构更容易失效，因此，考虑结构可靠性的动态连续体拓扑优化方法的研究具有重要理论意义和工程实际价值.

基于此，本文提出一种基于可靠性的动态连续体拓扑优化方法，尝试解决自由振动结构拓扑优化时考虑结构可靠度的难题.实际工程制造误差可能造成结构几何尺寸和体积的不确定性，假设这些不确定性变量服从高斯分布，利用一次二阶矩法计算结构的可靠度（可靠性指标），并作为约束参与到动态拓扑优化循环中.而结构可靠性分析也属于一个优化过程，因此，整个优化过程属于二次嵌套优化.考虑到连续体拓扑优化设计变量数量庞大，导致计算效率十分低下，无法实际应用，为突破该瓶颈，提出一种解耦策略，将二次嵌套优化循环解耦成两个独立的单独优化循环，大大提高了计算效率.建立以结构第一阶固有频率最大为优化目标，以体积和可靠度指标为约束的连续拓扑优化问题，用各向同性材料惩罚模型惩罚连续设计变量，并利用移动渐进方法求解该优化问题.所提方法可以得到一系列满足设计人员不同可靠度需求的拓扑结构，具有重要的工程意义.

1 动态拓扑优化方法

工程结构受到动态载荷时，设计人员往往希望结构固有频率偏离驱动频率，以防止共振发生.未考虑阻尼时，自由振动系统的微分方程为：

M+Ku=F=0（1）

式中：M为系统质量矩阵；K为系统刚度矩阵；u和分别为系统位移和加速度；F为系统所受外力，自由振动系统中其为一个零向量.

对式（1）进行拉普拉斯变换：

MU（s）s2+KU（s）=0（2）

令s=jω，可以得到：

[K-ω2iM]ui=0（3）

式中：ωi为系统第i阶固有频率；ui是响应的特征向量.

固有频率可以写成：

ω2i=kimi=uTiKuiuTiMui（4）

式中：ki和mi分别为模态刚度矩阵和模态质量矩阵.

在动力学拓扑优化研究中，比较常用的研究目标是使结构的第一阶固有频率最大，并受一定的体积约束，即：

to find：ρ1，…，ρe，…，ρN

maximizeρ：ω21=uT1Ku1uT1Mu1

subject to：[K-ω21M]u1=0，

：∑Ne=1veρe≤V0，

：0<ρmin≤ρe≤1，e=1，…，N.（5）

式中：ρe为单元密度；ρmin的设定是为了防止发生奇异解，一般取ρmin=0.001；N为单元个数；ve和V0分别为单元体积和设计允许的最终体积.

利用各向同性材料惩罚模型对连续密度进行惩罚，文中分别对单元刚度矩阵和单元质量矩阵进行惩罚，惩罚策略如下：

Ke=（ρe）p1K0（6）

Me=（ρe）p2M0（7）

式中：Ke和Me分别为单元刚度矩阵和单元质量矩阵；K0和M0分别为实体单元刚度矩阵和单元质量矩阵；ρ1和ρ2为值均大于1的惩罚系数，为了在优化过程中抑制中间密度的产生，传统方法视ρ1和ρ2为相同的值，但是研究发现，这样对中间密度的抑制并不理想.因此，本文采用一种新的惩罚策略，取ρ1和ρ2为不同的值，即：

當ρ≤ρe≤1，p1=3；

当ρmin≤ρe≤0.1，p1=0.01；

当0<ρmin≤ρe≤1，p2=1.

问题（5）是一个非凸优化问题，可用移动渐进方法（MMA）[31]进行高效求解.MMA将初始非凸优化问题近似为许多独立的、小的凸优化子问题，并对之进行高效求解.利用MMA需要首先得到目标函数对设计变量的一阶偏导数：

ω21ρe=uT1Kρeu1uT1Mu1-uT1Mρeu1uT1Ku1（uT1Mu1）2

=uT1Kρe-ω21Mρeu1uT1Mu1（8）

将材料惩罚策略代入式（8）中，得到：

ω21ρe=（ue1）[p（ρe）p1-1K0-ω21p2（ρe）p2-1M0]ue1uT1Mu1（9）

以式（9）为梯度信息，MMA可以快速且高效求解式（5）的动态拓扑优化问题.但是，不确定性是结构设计中无法避免的，例如，由于制造误差造成的结构尺寸不确定性、材料自身的不确定性和结构使用过程中加载力的不确定性等.而上述动态拓扑优化问题并未考虑结构的不确定性，所设计出的结构往往存在较高的失效概率.因此，文章尝试将结构不确定性引入到动态拓扑优化中，设计出满足一定结构可靠度要求的结构.

2 基于可靠性的动态拓扑优化方法

基于可靠性的连续体拓扑优化方法有较多学者进行了研究，但大多数局限于静力学结构的优化设计.将可靠性分析与动态拓扑优化问题相结合更具有挑战性.

2.1 问题提出

基于可靠性的动态拓扑优化方法旨在提高所设计结构的可靠度水平，当结构可靠度作为拓扑优化的一个约束时，利用可靠性指标法，优化问题（5）变为：

to find：ρ1，…，ρe，…，ρN

maximizeρ：ω21=uT1Ku1uT1Mu1

suject to：[K-ω21M]u1=0，

：g1=∑Ne=1veρe-V0≤0，

：g2=β0j-βj（ρe，μγ）≤0，j=1，…，m，

：0<ρmin≤ρe≤1，e=1，…，N，（10）

其中，结构可靠性指标的求解如下：

maximizeμγ：βj（η）=‖η‖suject to：Gj（d，η）=0（11）endprint

式中：g1和g2為不等式约束，分别控制体积和结构可靠度；β0j和βj分别为第j个结构可靠性指标目标值和第j个结构可靠性指标；m指结构系统一共有m个可靠度约束；μγ为结构不确定性变量均值；Gj（·）为在标准正态空间中第j个结构的功能函数，当Gj（·）>0时认为结构处于可靠状态，当Gj（·）<0时认为结构处于失效状态，Gj（·）=0时为结构极限状态；‖·‖指向量的范数；η为不确定性变量在标准正态坐标系中的形式.

利用伴随法可以求得式（10）优化问题的敏感系数，然后利用MMA进行求解.然而，该问题求解属于二次嵌套优化问题，即结构动态拓扑优化每次迭代循环都需要判断该次迭代结果是否满足所需结构可靠度要求，而结构可靠性分析也是一个优化问题.直接求解计算效率十分低下，不适合实际工程应用.因此，文章提出一种解耦策略，将二次嵌套优化问题转化为两个单独的优化循环，大大提高了计算效率.

2.2 解耦策略

不确定性变量用Y度量，Y=（Y1，…，Yt），结构拥有t个不确定变量，其均值和方差分别为μγ和σ2Y.这些不确定性变量对结构可靠性分析具有重要影响，然而，它们对结构固有频率并不一定有很大的影响.因此，需要首先计算目标函数对不确定性变量的敏感性，选择对目标函数影响大的不确定性变量，去除影响小的不确定性变量.这里使用有限差分法[32]：

ω21μY1=δω21δμY1=ω21（μY1+δμY1）-ω21（μY1）δμY1（12）

式中：μYtμYt=0.005.

确定对目标函数贡献大的不确定性变量后，需要确定可靠性指标对不确定性变量的梯度信息以每个迭代步更新可靠性指标.不确定性变量首先转化为标准正态分布：

η=Y-μYσY（13）

此时，结构的可靠性指标为：

β=∑η2t（14）

可靠性指标对不确定变量的一阶导数可以显式表达：

ε=βηt=ηtβ（15）

利用式（15）的梯度信息可以在每一迭代步更新结构可靠性指标的值.

为了将结构可靠性分析解耦出来，首先给出一个初始猜测值η，将该猜测值代入式（14）中计算可靠性指标.若该可靠性指标大于目标值，利用式（15）梯度信息更新其数值，直到满足目标值为止.此时，得到一个新的η*，进而可以得到在物理坐标系下的不确定性变量：

Y*=η*σY+μγ（16）

上式得到的是一个确定性向量，使用其作为拓扑优化的输入量所得到的拓扑结构，可以满足所需结构可靠度要求.这样，结构可靠性分析成功地从拓扑优化循环中解耦出来，大大提高了计算效率.需要指出的是，由于文章只关心线弹性结构的优化设计，故该解耦策略的精度可以接受.使用解耦策略的算法流程如图1所示.

3 数值算例

用一个标准算例来验证文章所提方法的有效性，同时说明动态拓扑优化设计考虑结构可靠性的重要性.这里只是为了验证算法的有效性，所有单位均无量纲处理.同时，使用了防止优化过程中棋盘格现象的策略[33]，得到边界光滑的拓扑结构.

两端固定梁的动态拓扑优化设计问题，如图2所示，长和宽分别为100和20，假设均服从正态分布，且离差均为0.02.初始域被离散为100×20个矩形单元.设计域材料的属性为：弹性模量为1，泊松比为0.3，密度为1，体积约束设为0.9，假设服从正态分布量，离差为0.02.

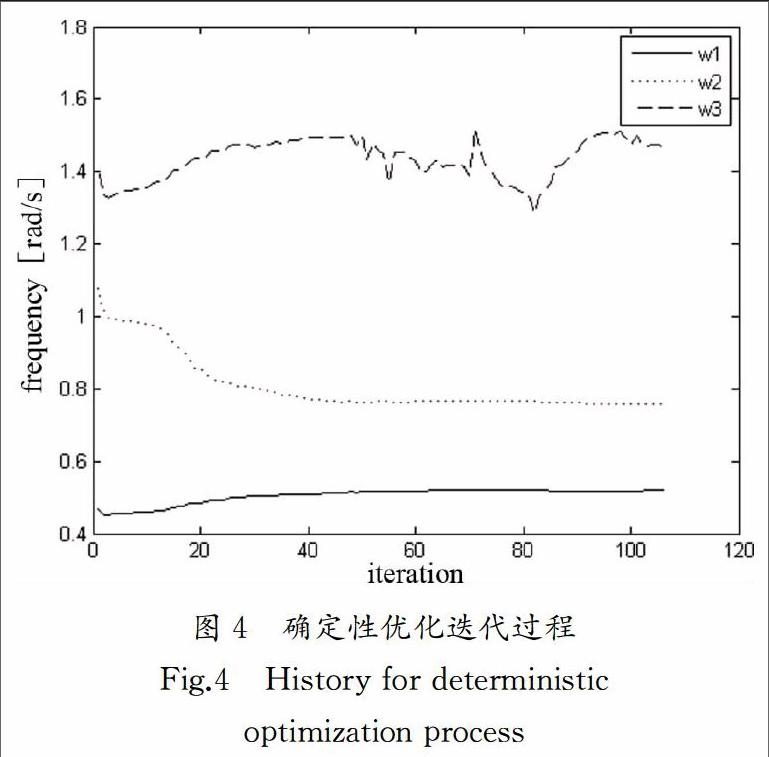
确定性动态拓扑优化所得结果如图3所示，拓扑结构边界光滑，便于实际结构制造.图4表明利用MMA求解动态拓扑优化问题收敛性良好，迭代106步后收敛，结构的第一阶固有频率为0.574 7，图中也给出了结构的第二阶和第三阶固有频率.

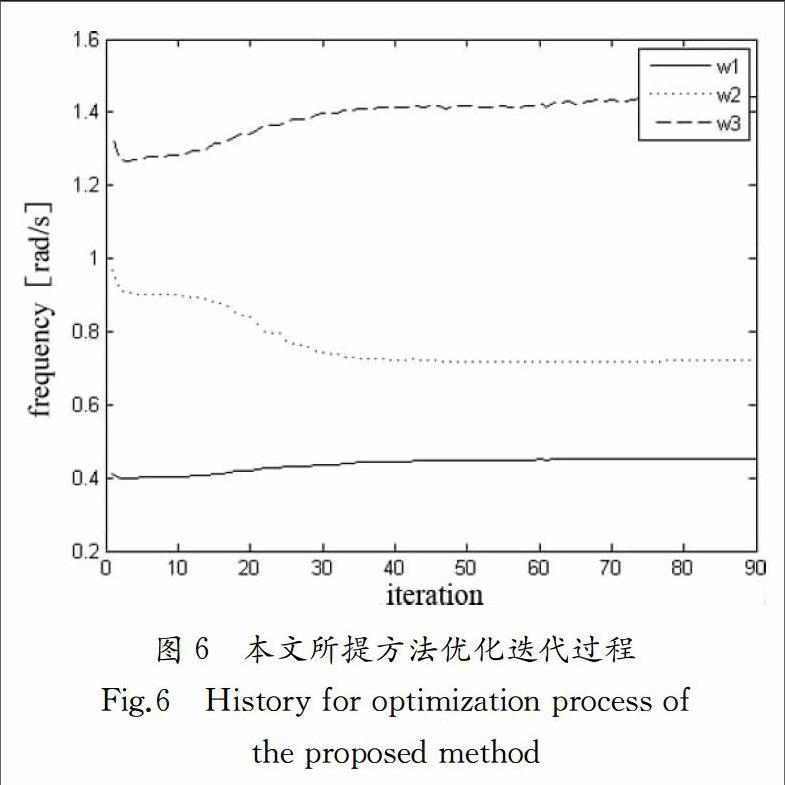
然而，在实际制造加工中误差无法避免，由误差导致的结构不确定性，在图3结构中并未考虑，该结构在实际工程服役过程中往往会存在较大的失效概率.利用文中所提方法优化设计该梁结构，设定结构可靠性指标值β0=4.0，利用一次二阶矩可得结构的失效概率为pf=Φ（-β0）=0.000 032，所得拓扑结构（图5所示）有很高的可靠度，可以很好地应对复杂多变的不确定性服役环境，如制造误差等.所得拓扑结构明显与图3不同，可以更好地抵抗结构不确定性的变化.图6显示所提算法收敛性良好，目标函数迭代90步收敛为0.520 3.需要指出的是，图5中结构最终材料体积为0.916，大于确定性优化结果的09，这是由于结构需要更多的材料来提高自身的可靠度，这也和文献[26，27]研究结果一致.

4 结 论

文章将结构可靠性分析引入到连续体动态拓扑优化中，提出一种基于可靠性的连续体拓扑优化方法.同时，为了提高计算效率，提出一种新的解耦策略，将结构可靠度计算约束从拓扑优化循环中解耦出来，大大提高了计算效率.得出以下结论；

1）考虑了由于制造误差等造成的几何尺寸和体积不确定性，设计出的结构可以满足设计人员的可靠度要求，可以更好地应对复杂的不确定性的服役环境.

2）设计出的结构相对于确定性优化结构拥有更多的材料，拥有更高的可靠度.

3）所提算法有很好的收敛性，迭代过程平稳，并得到边界光滑的拓扑结构.

参考文献

[1] LI C，KIM I Y，JESWIET J. Conceptual and detailed design of an automotive engine cradle by using topology，shape，and size optimization[J]. Structural and Multidisciplinary Optim-ization，2015，51（2）； 547-564.

[2] TOLEDO R，AZNREZ J J，GREINER D，et al. Shape design optimization of road acoustic barriers featuring top-edge devices by using genetic algorithms and boundary elements[J]. Engineering Analysis with Boundary Elements，2016，63：49-60.endprint

[3] BENDSE M P，KIKUCHI N. Generating optimal topologies in structural design using a homogenization method[J]. Computer Methods in Applied Mechanics and Engineering，1988，71（2）：197-224.

[4] SIGMUND O. A 99 line topology optimization code written in Matlab[J]. Structural and Multidisciplinary Optimization，2001，21（2）： 120-127.

[5] BENDSE M P，SIGMUND O. Topology optimization：theo-ry，methods，and applications[M]. Springer Science & Business Media，2013：100-102.

[6] WANG M Y，WANG X，GUO D. A level set method for structural topology optimization[J]. Computer Methods in Applied Mechanics and Engineering，2003，192（1）： 227-246.

[7] XIE Y M，STEVEN G P. Basic evolutionary structural optimization[M]. London：Springer，1997：74-75.

[8] 隋允康，杨德庆，王备. 多工况应力和位移约束下连续体结构拓扑优化[J]. 力学学报，2000，32（2）： 171-179.

SUI Yongkang，YANG Deqing，WANG Bei. Topological optimization of continuum structure with stress and displacement constraints under multiple loading cases[J]. Acta Mechanica Sinica，2000，32（2）： 171-179. （In Chinese）

[9] ZHOU M，LAZAROV B S，WANG F，et al. Minimum length scale in topology optimization by geometric constraints[J]. Computer Methods in Applied Mechanics and Engineering，2015，293： 266-282.

[10]GUEST J K. Optimizing the layout of discrete objects in structures and materials：a projection-based topology optimization approach[J]. Computer Methods in Applied Mechanics and Engineering，2015，283： 330-351.

[11]LPEZ C，BALDOMIR A，HERNNDEZ S. Deterministic versus reliability-based topology optimization of aeronautical structures[J]. Structural and Multidisciplinary Optimization，2016，53（4）： 907-921.

[12]DUDDECK F，HUNKELER S，LOZANO P，et al. Topology optimization for crashworthiness of thin-walled structures under axial impact using hybrid cellular automata[J]. Structural and Multidisciplinary Optimization，2016，54（3）：415-428

[13]张伟，侯文彬，胡平. 基于拓扑优化的电动汽车白车身优化设计[J]. 湖南大学学报：自然科学版，2014，41（10）：42-48.

ZHANG Wei，HOU Wenbin，HU Ping. The body in white optimization of an electric vehicle using topology optimization[J]. Journal of Hunan University：Natural Sciences，2014，41（10）：42-48.（In Chinese）

[14]劉志文，辛亚兵，陈政清. 铝合金桥面板合理断面形式拓扑分析和优化[J]. 湖南大学学报：自然科学版，2010，37（1）；11-16.

LIU Zhiwen，XIN Yabing，CHEN Zhengqing. Topologic analysis and optimization of reasonable cross-section of aluminum alloy bridge decks[J]. Journal of Hunan University：Natural Sciences，2010，37（1）：11-16.（In Chinese）

[15]LIU J，WEN G，QING Q，et al. An efficient method for topology optimization of continuum structures in the presence of uncertainty in loading direction[J]. International Journal of Computational Methods，2017，14（2）：1750054.endprint

[16]LIU J，WEN G，XIE Y M. Layout optimization of continuum structures considering the probabilistic and fuzzy directional uncertainty of applied loads based on the cloud model[J]. Structural and Multidisciplinary Optimization，2016，53（1）： 81-100.

[17]LIU J，WEN G，HUANG X. To avoid unpractical optimal design without support[J]. Structural and Multidisciplinary Optimization，2017： 1-7.

[18]LIU J，QING Q，DENG Y，et al. Fatigue reliability study on T-welded component considering load shedding[J]. Fatigue & Fracture of Engineering Materials & Structures，2015，38（7）：780-788.

[19]LIU J，WEN G. Continuum topology optimization considering uncertainties in load locations based on the cloud model[J]. Engineering Optimization，2017： 1-20.

[20]BEYER H G，SENDHOFF B. Robust optimization-a comprehensive survey[J]. Computer Methods in Applied Mechanics and Engineering，2007，196（33）：3190-3218.

[21]VALDEBENITO M A，SCHUЁLLER G I. A survey on approaches for reliability-based optimization[J]. Structural and Multidisciplinary Optimization，2010，42（5）：645-663.

[22]KHARMANDA G，OLHOFF N，MOHAMED A，et al. Reliability-based topology optimization[J]. Structural and Multidisciplinary Optimization，2004，26（5）： 295-307.

[23]JUNG H S，CHO S. Reliability-based topology optimization of geometrically nonlinear structures with loading and material uncertainties[J]. Finite Elements in Analysis and Design，2004，41（3）： 311-331.

[24]MAUTE K，FRANGOPOL D M. Reliability-based design of MEMS mechanisms by topology optimization[J]. Computers & Structures，2003，81（8）： 813-824.

[25]KANG Z，LUO Y. Non-probabilistic reliability-based topology optimization of geometrically nonlinear structures using convex models[J]. Computer Methods in Applied Mechanics and Engineering，2009，198（41）：3228-3238.

[26]SILVA M，TORTORELLI D A，NORATO J A，et al. Component and system reliability-based topology optimization using a single-loop method[J]. Structural and Multidisciplinary Optimization，2010，41（1）： 87-106.

[27]NGUYEN T H，SONG J，PAULINO G H. Single-loop system reliability-based topology optimization considering statistical dependence between limit-states[J]. Structural and Multidisciplinary Optimization，2011，44（5）： 593-611.

[28]ZHAO Q，CHEN X，MA Z D，et al. Reliability-based topology optimization using stochastic response surface method with sparse grid design[J]. Mathematical Problems in Engineering，2015，2013（1）：1-13.

[29]LIU J，WEN G，ZUO H Z，et al. A simple reliability-based topology optimization approach for continuum structures using a topology description function[J]. Engineering Optimization，2016，48（7）： 1182-1201.

[30]JALALPOUR M，TOOTKABONI M. An efficient approach to reliability-based topology optimization for continua under material uncertainty[J]. Structural and Multidisciplinary Optimization，2016，53（4）： 759-772.

[31]SVANBERG K. The method of moving asymptotes—a new method for structural optimization[J]. International Journal for Numerical Methods in Engineering，1987，24（2）：359-373.

[32]LIPNIKOV K，MANZINI G，SHASHKOV M. Mimetic finite difference method[J]. Journal of Computational Physics，2014，257（1）： 1163-1227.

[33]POULSEN T A. A simple scheme to prevent checkerboard patterns and one-node connected hinges in topology optimization[J]. Structural and Multidisciplinary Optimization，2002，24（5）： 396-399.endprint