一种基于广度优先搜索的移动对象轨迹简化算法
杨 彪,杨智应
(上海海事大学 信息工程学院,上海 201306)
一种基于广度优先搜索的移动对象轨迹简化算法
杨 彪,杨智应
(上海海事大学 信息工程学院,上海201306)
移动对象产生的轨迹数据在许多实际应用中起着至关重要的作用。目前对移动对象轨迹简化方法的研究或多或少依赖轨迹的几何特性。这些方法没有突出移动对象的速度这一重要特征。文章介绍了基于速度的移动对象轨迹简化新方法,提出了基于广度优先搜索算法的多项式时间算法及其优化算法,通过大量实验证明所提出算法在权衡轨迹的简洁性和精确性上比DP算法、SP算法有较大优势。
移动对象;离线轨迹简化;速度阈值
0 引言
随着GPS嵌入式设备的激增(例如智能电话和出租车),移动对象轨迹数据变得无处不在。在过去十多年中,人们对移动对象数据库(MOD)已进行了广泛的研究[1]。移动轨迹数据通常通过周期性地收集移动物体的位置而获得。
然而现在提出的轨迹简化算法要么去掉过多的轨迹特征点,使简化后的轨迹与原始轨迹偏差较大,精确度不高;要么保留了过多的轨迹点,使存储成本上升,简洁度不够。为了解决这个问题,本文提出了v-bfs算法,在权衡轨迹的简洁性和精确性上有较大的优势。
1 相关工作
在最近的研究中,文献[2]中提出了基于方向的轨迹简化算法,通过给定的角度阈值来简化轨迹,使求出的简化轨迹最大角度值不大于给定的角度阈值。在文献[2]的基础上,文献[3]中提出了简化轨迹的数量在不大于给定值的情况下,使得简化轨迹与原始轨迹方向阈值最小的简化算法;文献[4]提出了基于方向的实时简化算法。
另一类轨迹简化算法以垂线距离或同步欧氏距离为误差度量指标。文献[5]中提出的DP算法以垂线距离作为误差度量指标来简化轨迹。Keogh等人基于垂线距离提出了实时压缩算法。文献[6]中对DP算法作了改进,提出了以同步欧式距离为误差度量指标的轨迹简化算法。
此外,还有其他的轨迹简化算法,文献[7]利用语义信息来替代轨迹数据,进行轨迹简化。文献[8]提出了基于速度的轨迹简化算法。本文的轨迹简化思想与文献[8]有很大的不同,文献[8]的轨迹简化核心度量指标是关于轨迹段平均速度的比值,而本文轨迹核心度量指标为轨迹段的最大速度差值。
2 移动轨迹简化问题描述及算法
2.1一些定义及记号
定义1(位置点或轨迹点):位置点用p表示,p是一个三元组,组内对应属性分别代表该点的经度、纬度、时间,p=(x,y,t)。
定义2(原始轨迹):原始轨迹T是一些有序位置点的集合。
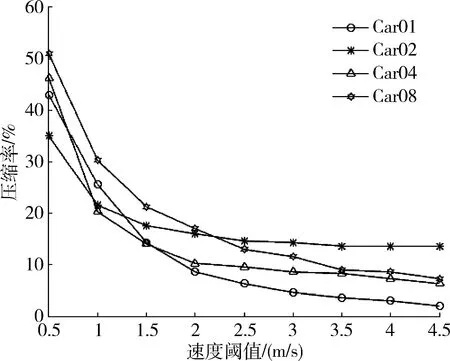
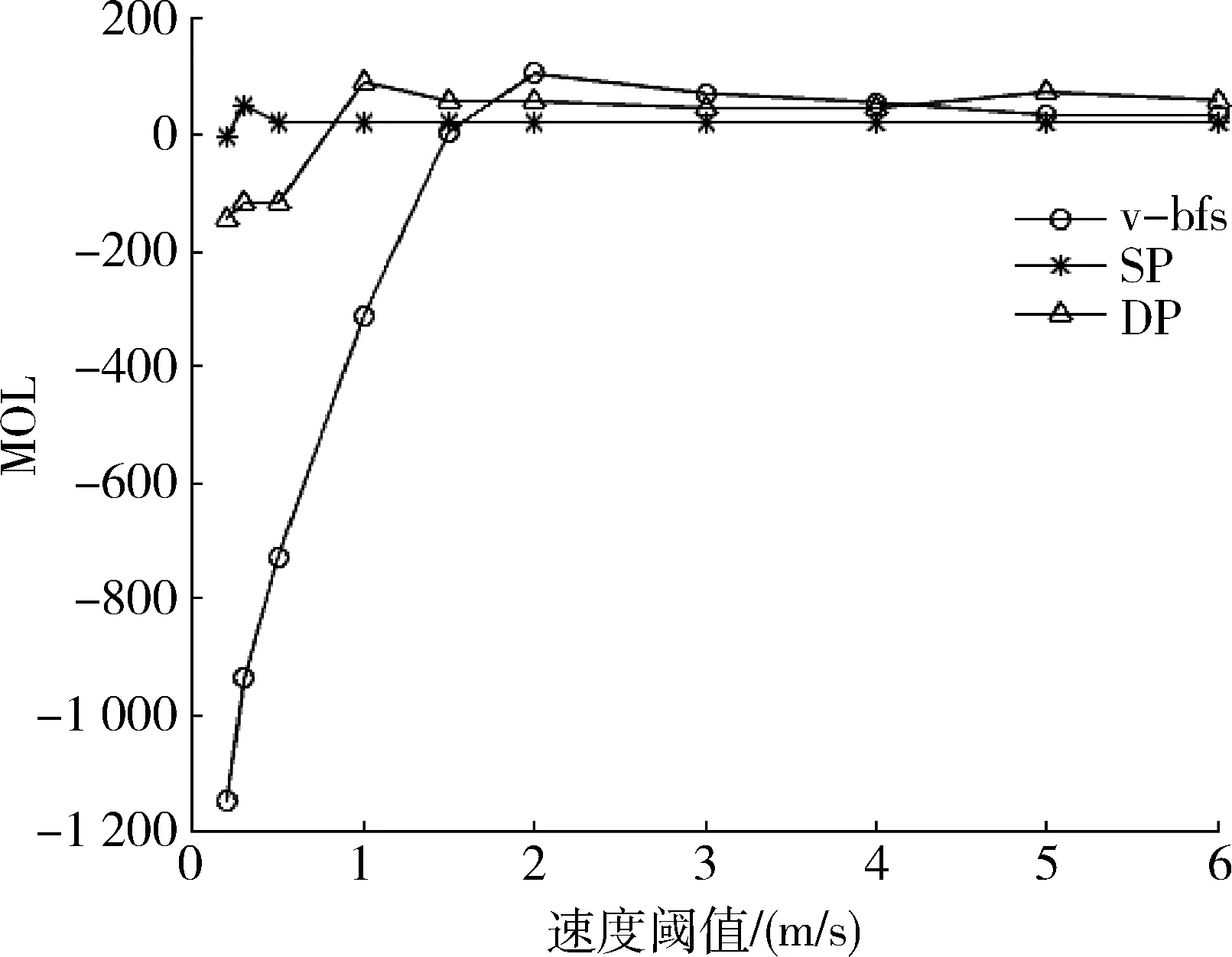
T=(p1,…,pi,…,pn)(i∈[1,n]),其中:pi=(xi,yi,ti)并且t1 定义3(原始轨迹的子轨迹):原始轨迹T的子轨迹用T[i,j]表示,也是一些有序位置点的集合,T[i,j]=(pi,pi+1,…,pj)(1≤i≤j≤n)。 定义4(简化轨迹):简化轨迹Tsim是原始轨迹T去掉一些位置点的有序集合。 Tsim=(ps1,ps2,…,psm)(1≤s1 原始轨迹T中位置点的个数用|T|表示,则T中轨迹段的个数为|T|-1或n-1。简化轨迹Tsim中位置点的个数用|Tsim|表示,则Tsim中轨迹段的个数为|Tsim|-1或m-1。 如图1所示,假定原始轨迹T=(p1,p2,…,p8),简化后的轨迹Tsim=(p1,p4,p6,p8),原始轨迹T的轨迹段用实心黑线表示,简化轨迹Tsim的轨迹段用实心虚线表示;此时|T|=8,|Tsim|=4。 图1 原始轨迹和简化轨迹 定义9(简化轨迹Tsim的最大速度差值):简化轨迹Tsim中,对任意位置点psk(k∈[1,m)),简化轨迹Tsim的最大速度差值用ε(Tsim)表示。 2.2基于速度的轨迹简化问题 问题描述:T是原始轨迹,Tsim是T的简化轨迹,εv是一个预先给定的速度阈值。如果T有多条简化轨迹满足ε(Tsim)≤εv,如何找到一条简化轨迹Tsim,使简化轨迹Tsim的轨迹点最少? 本文采用了轨迹段的最大速度差值而不是平均速度差值,因为最大速度差值更能突显出轨迹速度变化的剧烈程度。为了解决上述描述的问题,本文提出了以下多个算法来解决该问题:(1)基于广度优先搜索的简化算法(v-bfs算法);(2)v-bfs算法的优化算法(v-bfs-imp算法),并通过大量的实验来说明v-bfs算法在权衡轨迹的简洁性和精确性方面有较大优势。 2.3基于广度优先算法的简化算法(v-bfs算法) 该算法运用图的广度优先搜索算法(BFS)来求解简化轨迹大小|Tsim|最小值问题,称该算法为v-bfs算法,构造步骤如下: (2)寻找最短路径。在图Gεv(V,E)中用广度优先搜索算法(BFS)寻找一条从p1到pn的最短路径。 (3)找到图的简化轨迹。根据第(2)步的路径关系找到一条简化轨迹。 为了进一步降低该算法的时间和空间复杂度,提出该算法的优化算法。 2.4v-bfs算法的优化算法(v-bfs-imp算法) 优化算法的目的是为了降低算法的时间复杂度,在提出优化算法之前先介绍几个概念。 定义11(子轨迹的速度变化范围):在子轨迹T[i,j]中,fvr(T[i,j]|εv)为子轨迹中各个轨迹段的速度变化范围的交集,子轨迹T[i,j]的速度变化范围用fvr(T[i,j]|εv)表示。 根据引理2,可以证明相同的轨迹经过v-bfs算法和v-bfs-imp算法得到相同的简化轨迹,只是v-bfs-imp算法时间复杂度降低了一个数量级,空间复杂度还是O(V+E)。 为了分析与评估算法的性能,实验选取笔记本电脑作为硬件测试平台,具体配置如下:处理器为英特尔Pentium(奔腾)P6200@2.13 GHz 双核,内存为6 GB;实验环境为 Windows 7 操作系统和 Eclipse开发系统,Java语言实现。实验数据从项目INFATI得到[9],INFATI 的位置数据由20个有效的GPS 数据集构成。 3.1度量指标 轨迹简化应该具有以下两个期望的性质:简洁性和精确性。简洁性意味着简化后的轨迹数量尽可能少。精确性意味着简化轨迹应该与原始轨迹差异尽可能小。然而既要高精度又要高简洁度是不可能,精确性与简洁性之间是相互矛盾的,只能在两者之间找平衡点。文献[10]用L(H)表示简化轨迹与原轨迹之间简洁度的偏差,用L(D|H)表示简化轨迹与原轨迹之间精确度的偏差。MDL表示简化轨迹与原始轨迹总偏差,根据文献[10]中公式(1)、(3)、(6)、(7),分别罗列出这三个变量的定义: L(D|H)=L(D|H)_position+L(D|H)_direction MDL=L(H)+L(D|H) 3.2不同轨迹数据对轨迹压缩率的影响 选取4条不同的轨迹,每条轨迹选取300个连续的GPS轨迹点,采用相同的v-bfs算法进行轨迹简化,当速度阈值εv从0.5 m/s逐渐增大到4.5 m/s时,简化轨迹的轨迹点与原始轨迹的轨迹点的比值变化如图2所示。 图2 不同速度阈值的简化轨迹轨迹点与原始轨迹轨迹点的比值 从图2中可以看出随着εv逐渐增大,简化后的轨迹数逐渐减小;其中任意两条轨迹,在相同的速度阈值下,轨迹简化率各不相同,简化率的差值也在不断变化。 3.3算法比较(v-bfsvsDPvsSP) 用本文提出的v-bfs算法来和DP算法、SP算法比较,用以上3个指标来度量算法在权衡轨迹简洁度和精确度上的优劣性。 采用DP算法[5]来作为比较对象,因为该离线算法是纯粹的基于位置信息来简化轨迹,同时也是非常著名的算法。采用SP算法[2]作为比较对象,因为该离线算法同样是纯粹地基于方向信息来简化轨迹。算法的时间复杂度和空间复杂度比较如表1。 表1 算法时间复杂度与空间复杂度 对每一个速度阈值εv,用算法v-bfs得到简化轨迹Tsim,根据文献[2]中公式(2)求出简化轨迹Tsim与原始轨迹T的角度偏差,作为SP算法的输入值。 用相同的简化轨迹Tsim求出每个轨迹段的轨迹点到轨迹两端点的最大垂线距离,所有轨迹段垂线距离的最大值即为DP算法的输入值。 在图3中,v-bfs算法和DP算法的L(H)值随着εv的增大而逐渐变小,当εv等于6.0 m/s时,L(H)近似相等,然而SP算法L(H)值先变小然后保持不变;表明v-bfs算法在εv较小时能保证简化轨迹与原始估计的方向偏差;然而εv大于0.5 m/s时,简化轨迹与原始估计的方向偏差非常大。图3表明v-bfs算法的简洁性均没有DP算法和SP算法好。 图3 L(H)值比较 在图4中,三种算法的L(D|H)的值均随着εv的增大先增大后保持不变,且L(D|H)在保持不变前,v-bfs算法的轨迹一直处于另外两条轨迹的下方,说明v-bfs算法比DP算法和SP算法保留了更多原始轨迹的信息。表明经过v-bfs算法简化后的轨迹比SP算法和DP算法的精确度更高。 图4 L(D|H)值比较 在图5中,当速度阈值εv小于1.5 m/s时,v-bfs算法在权衡简洁度和精确度上都要比DP算法和SP算法好;速度阈值εv大于1.5 m/s时,经过三种算法后的简化轨迹与原始轨迹的总偏差大体上相差不大,并且随着εv的逐渐增大,这三种算法效果一样。 图5 MDL值比较 总的来说,v-bfs算法在简洁度上比SP算法和DP算法差,在精确度上比SP算法和DP算法要好,在权衡简洁性和精确性上比SP算法和DP算法也要好。 本文提出了基于速度的轨迹简化新思路,并且提出了基于广度优先搜索的轨迹简化算法及其优化算法,通过实验比较得出,v-bfs算法在权衡简洁性和精确性上比SP算法和DP算法有较大优势。将来为了进一步缩短轨迹压缩时间,将考虑如何实现基于速度的轨迹压缩实时简化算法。 [1] PATEL D,SHENG C,HSU W,et al.Incorporating duration information for trajectory classification[C].IEEE International Conference on Data Engineering.IEEE,2012:1132-1143. [2] CHENG L,WONG C W,JAGADISH H V.Direction-preserving trajectory simplification[J].Proceedings of the Vldb Endowment,2013,6(10):949-960. [3] CHENG L,WONG C W,JAGADISH H V.Trajectory simplification: on minimizing the directionbased error[J].Proceedings of the Vldb Endowment,2014,8(1):49-60. [4] DENG Z,HAN W,WANG L,et al.An efficient online direction-preserving compression approach for trajectory streaming data[J].Future Generation Computer Systems,2017,68:150-162. [5] DOUGLAS D H,PEUCKER T K.Algorithms for the reduction of the number of points required to represent a digitized line or its caricature[J].Cartographica the International Journal for Geographic Information & Geovisualization,1973,10(2):112-122. [6] MERATNIA N,BY R A D.Spatiotemporal compression techniques for moving point objects[C].Advances in Database Technology-EDBT 2004,International Conference on Extending Database Technology,Heraklion,Crete,Greece,2004:765-782. [7] RICHTER K F,SCHMID F,LAUBE P.Semantic trajectory compression: representing urban movement in a nutshell[J].Journal of Spatial Information Science,2012,4(4):3-30. [8] YING J C,SU J H.On velocity-preserving trajectory simplification[C].Intelligent Information and Database Systems,2016: 241-250. [9] JENSEN C S,LAHRMANN H,PAKALNIS S,et al.The infati data[J].Computer Science,2004,29(3):449-473. [10] LEE J G,HAN J,WHANG K Y.Trajectory clustering: a partition-and-group framework[C].ACM SIGMOD International Conference on Management of Data.ACM,2007:593-604. A moving object trajectory simplification algorithm based on breadth-priority search Yang Biao,Yang Zhiying (School of Information Engineering,Shanghai Maritime University,Shanghai 201306,China) The trajectory data generated by the moving object plays a vital role in many practical applications.At present,the study of the moving object trajectory simplification method is more or less dependent on the geometric characteristics of the trajectory.These methods do not highlight the important feature of the moving speed of the object.In this paper,we introduced a new method to simplify the trajectory of moving objects based on speed,and proposed a polynomial time algorithm based on breadth-first search algorithm and its optimization algorithm.Through a large number of experiments,we proved that the proposed algorithm has a great advantage over the DP algorithm and the SP algorithm in the simplicity and accuracy of the trade-off trajectory. moving object; offline trajectory simplification; speed threshold TP301 A 10.19358/j.issn.1674-7720.2017.21.022 杨彪,杨智应.一种基于广度优先搜索的移动对象轨迹简化算法J.微型机与应用,2017,36(21):74-77. 2017-04-12) 杨彪(1992-),男,硕士,主要研究方向:移动对象数据库。 杨智应(1964-),男,博士,教授,主要研究方向:算法与复杂性、移动计算、分布式计算与软件工程。

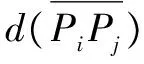



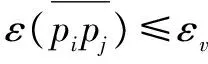



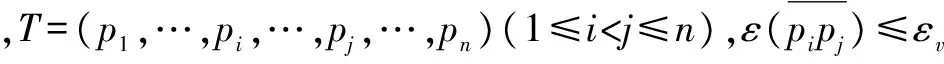
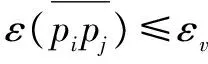


3 实验比较



4 结论

