泄压条件下气体爆炸超压计算模型研究
袁丹灿,马 斌,杜坤泽
(武警学院 研究生队,河北 廊坊 065000)
泄压条件下气体爆炸超压计算模型研究
袁丹灿,马 斌,杜坤泽
(武警学院 研究生队,河北 廊坊 065000)
基于封闭空间压力增长理论和泄放质量比例的压力衰减假设,建立泄压条件下气体爆炸超压变化的微分方程模型,并通过固定时间差分离散将其转化为差分方程模型,给出差分方程的求解步骤。对模型求解进行时间差分的敏感性分析,得到时间差分的大小应控制在0.001 s以下。根据Bartknecht在1 m3且有0.36 m2泄压口的正方体空间内进行的甲烷爆炸系列试验进行求解对比,分析了模型的适用条件、误差因素和湍流因子的误差机理。分析表明:对于体积为1 m3且泄压面积为0.36 m2空间内的甲烷爆炸,在泄压构件相对静态触发压力介于20~200 kPa条件下模型适用;应用于其他条件时,应当考虑通过燃爆指数折算的湍流因子的适用范围。
气体爆炸;防爆泄压;超压模型;湍流因子
0 引言
泄压是降低爆炸破坏最有效的手段,通过布置泄压构件可以在爆炸全面发展之前及时将压力泄放,从而降低爆炸可能产生的最大超压,进而防止对结构造成破坏。工程上常根据结构强度确定泄压条件下空间内部允许最大超压,并以此为根据指导泄压设计[1-3]。针对可燃气体,Swift[4]提出泄压面积应与允许最大超压的平方根成反比,Bartknecht[5]则提出了该压力与气体燃爆指数共同决定泄压面积的非线性经验模型。部分学者通过研究压力变化规律,分析压力产生机理以确定泄压条件下的最大超压:Zalosh等[6-8]认为无量纲的压力可用无量纲泄压面积的函数关系表征,Hernandez[9]等基于已燃和未燃气体组分变化建立了微分方程计算泄压条件下封闭空间内压力的演化过程,Chyzy[10]等用正弦关系描述压力变化过程进而简化了求解超压的微分方程模型。本文基于一定的简化假设,建立泄压条件下气体爆炸超压的微分方程模型及求解的差分方程模型,并对模型的适用性与局限性进行探讨。
1 泄压条件下气体爆炸超压微分方程模型
1.1 泄压口未开启下的压力增长规律
将空间内气体视为整体,假设压力分布均匀,在泄压构件开启之前空间封闭。空间内部压力P的增长率与燃烧半径rb有关。在长径比L/D<2的条件下,可以认为火焰面以球面的形式从点火源向各个方向等效传播,有
式中,t是时间,s;Su是气体的基本燃烧速度,m·s-1;χ是湍流因子;a是空间的当量半径,m;Pm是封闭空间内气体爆炸产生的最大压力,kPa;P0是初始的环境压力,kPa;γ是气体绝热指数。
燃烧半径的增长又与爆炸压力有关
根据式(1)和式(2),给定初始条件ε=(rb/a)→0即可求解空间压力的变化过程。
式(1)中χ的变化规律相对复杂,与物质类型和压力的增长过程等诸多因素相关。对于气体的类型,可以通过立方体定律表述
式中,KG是气体燃爆指数,bar·m·s-1。在绝热假设下,压力的增长不会出现拐点,因此(dP/dt)max应在P=Pmax处达到,有
故可以据此倒推估算湍流因子
将式(5)所得湍流因子视为常量,代入式(1)、式(2)求解压力P,即可得到空间内压力变化规律。
1.2 泄压口开启下的压力变化规律
忽略泄压构件的动作规律,假设达到其静态触发压力Pstat时泄压口完全打开,其面积为Av,m2。此时空间内气体由于超压将通过泄压口向外泄放。判断气流的流态:若(P/P0)<[(γ+1)/2]γ /(γ-1),为亚声速流动,其泄放速率为
若(P/P0)≥[(γ+1)/2]γ /(γ -1),气流则为超声速流动,其泄放速率为
式(6)和式(7)中,mv是泄放的气体质量,kg;Cd是泄放系数,由泄压构件的形式决定;ρ是空间内气相平均密度,kg·m-3,随压力变化关系为
由于气体的泄放,空间内气相物质的质量减少,进而引起压力增长速率衰减。假设泄压作用下,空间内实际压力Pv可以用泄放的质量比例系数fvent来描述,则
此时空间内的压力增长速率也应由Pv决定,则式(1)、式(2)的P应相应作Pv,并以此求解压力变化规律,得到的峰值压力Pv,max对应的相对压力Pv,max-P0就是泄压条件下的最大超压。
2 固定时间离散的差分方程模型
2.1 差分离散模型的建立
为便于求解,将微分方程模型基于固定时间差分Δt进行离散。此时P与Pv可统一,差分关系为
式中,ti时刻的压力增量ΔPi为
ti时刻的气相泄放质量mv,i的差分关系(分亚声速和超声速两种流态)为
式(10)~(12)的差分模型中,rb、χ和ρ可分别依照式(2)、式(5)和式(8)计算,而泄压面积Ai可以简化为分段函数
2.2 差分方程的求解步骤
确定参数后,在确定的初始条件下便可通过差分方程模型求解压力变化过程和泄压条件下的最大超压(P-P0)max,模型中的压力均为绝对压力。其迭代求解算法如图1所示。
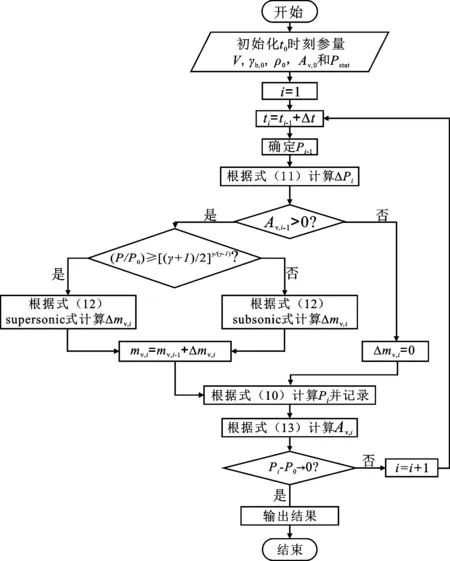
图1 差分方程求解流程框图
3 模型的验证与分析
3.1 时间差分的敏感性分析
差分离散的求解需要进行时间差分的敏感性分析,在本模型中即是针对时间差分的大小作敏感分析,以确定合适的Δt。现给定物质为甲烷,场景参数如表1所示,令Δt=0.01,0.005,0.002 5,0.001,0.000 5 s进行求解,其结果如图2所示。由图2可以看出:Δt的取值不同,模型求解的结果有一定偏差,当Δt<0.001 s之后,模型的求解结果已基本不受Δt取值的影响而趋于稳定。因此下文计算中,以Δt=0.001 s进行迭代求解可以得到稳定结果。
3.2 模型的可靠性分析
为验证模型的可靠性,以Bartknecht在1 m3且有0.36 m2泄压口的正方体空间内进行甲烷爆炸试验条件进行计算对比[11]。试验的实际条件参数如表2所示。为作区分,下文中用到的Pred指的是Bartknecht试验下测得的超压,而模型所计算的超压均记为P-P0。

表1 敏感性分析场景参数表

图2 求解的时间差分敏感性分析结果
由于泄压构件的形式未知,因此假定Cd=0.90,且认为当空间内部压力达到泄压构件静态触发压力的瞬间,泄压面积完全敞开至最大且不随压力的下降而减小;初始的火焰燃烧半径为0.001 m(rb,0/a=0.001 61→0)。计算与试验结果对比情况如表3所示,各工况下的压力变化过程如图3所示。
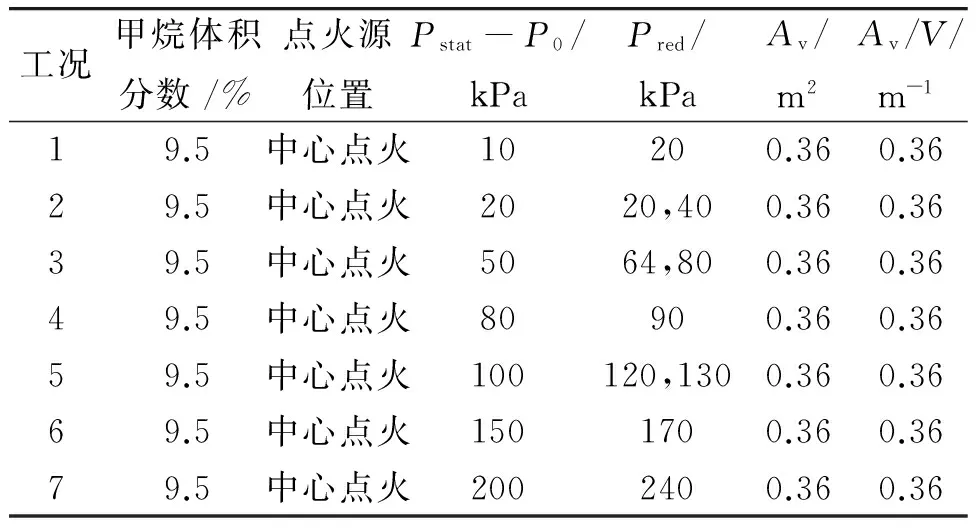
表2 Bartknecht甲烷爆炸试验条件参数汇总表

表3 模型-试验最大超压结果对比
由图3可见,无论Pstat大小如何,空间内部超压最初均按照相同的增速增长模式变化,这反映了在泄压构件未开启之前封闭空间的压力增长模式。当P-P0大于Pstat-P0时,曲线出现拐点且此处的导数不连续,这是由于此时Av的突变引起的,类似爆破片等形式泄压构件的动作模式;对于泄爆门等开口面积会随着压差大小变化的构件,超压曲线则不会有此突跃。由表3的对比结果,可说明该模型存在一定的适用范围:对于1 m3且泄压面积为0.36 m2空间内的甲烷爆燃,当Pstat-P0处于20 kPa以下时,模型计算相对误差较大,处于不可接受的范围;而当Pstat-P0达到一定程度(150 kPa以上),则相对误差又会有所增大。因此,有必要进行模型参数的敏感性分析,以确定影响该模型适用条件的相关因素。
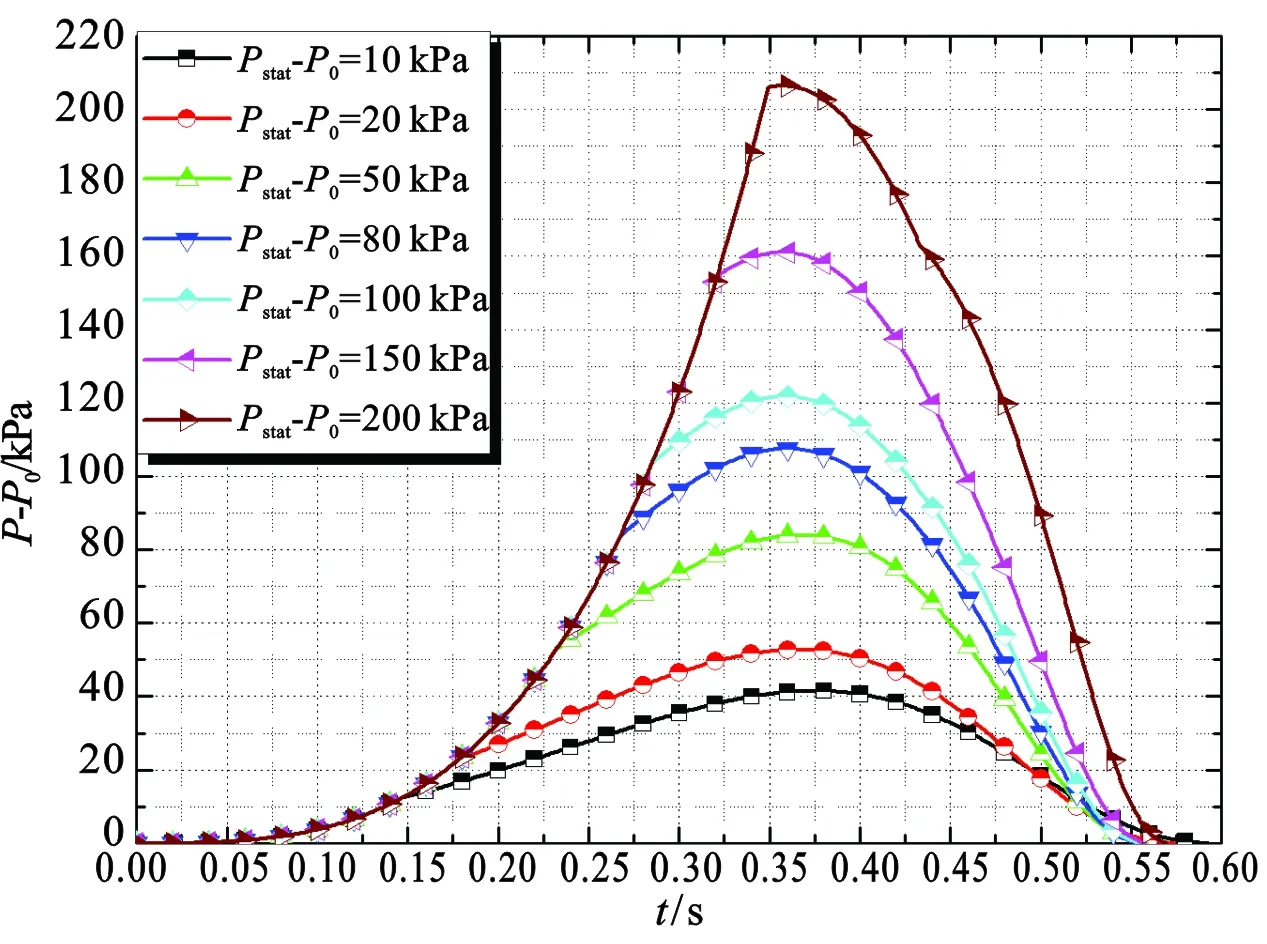
图3 Bartknecht甲烷爆炸试验的模型求解结果
3.3 参数的敏感性及误差分析
3.3.1 压力增长方式分析
现就3.2分析存在的问题,以表2的空间及物质条件,以2为等比梯度,分别求解在Pstat-P0从2.5~320 kPa下甲烷泄压爆炸所能产生的最大超压,对应的压力变化过程如图4所示,结果如表4所示。由图4可得:超压主要是取决于泄压后的过程。在Pstat-P0≤20 kPa时,超压的变化过程对泄压动作已不敏感,在泄压口开启之后压力继续增长的时间较长且增长压力相对接近;随着Pstat的增大,压力开始衰减的时间与泄压口动作的时间越来越接近,达到Pstat-P0≥320 kPa时,在泄压动作之后压力随即衰减而无法继续增长。此二因素是导致模型在Pstat过高或过低的工况下误差增大的主要原因。

图4 (Pstat-P0)系列等比梯度模型求解结果表4 等比梯度工况计算结果

计算参量等比梯度工况Pstat-P0/kPa2.5510204080160320Pmax-P0/kPa29.6532.8941.6852.6971.64107.48168324泄压动作时间/s0.0860.1090.1460.1770.2130.2660.3250.396衰减时间/s0.420.3990.3750.3660.3650.360.3570.397fvent,max0.9998880.9998790.9998210.9997790.9995970.9993990.9988960.997959fvent,min0.9953720.9950330.9941780.9931290.9914810.9890490.9864160.982043
现假设某个时刻ti存在Pi=(+)fvent>Pi-1,即(1-fvent)/fvent<ΔPi/Pi-1。由表4可得,fvent的值均在0.99左右,因此可认为不等式左侧为一常数,压力的增减主要由不等式右侧的增压比决定。该增压比与(P/P0)γ、{1-(P/P0)γ[(Pm-P)/(Pm-P0)]}2/3成正比,即与P成负相关关系。因此在其他参数为常数的条件下,只能依靠P增长到一定程度后才能使其压力衰减。因此,在其他参数保证可靠的前提下,该等比梯度系列计算结果是合理的。
3.3.2 湍流因子的敏感性及误差机理分析
相关研究表明,KG并不是一个常数,其大小会受到湍流作用的影响,在不同条件下的数值应不同。而本文模型使用的湍流因子是通过恒定的KG倒推得到,本身具有局限性;同时,模型中的其他参数也直接或间接与χ相关,故χ是模型误差的主要来源。现就表2工况1和工况7,以0.2的等差梯度研究χ=0.2~1.2的范围内超压的变化过程,得到的结果如表5、6所示,超压变化过程如图5、6所示。

表5 Pstat-P0=10 kPa工况下χ的敏感性分析结果

表6 Pstat-P0=200 kPa工况下χ的敏感性分析结果
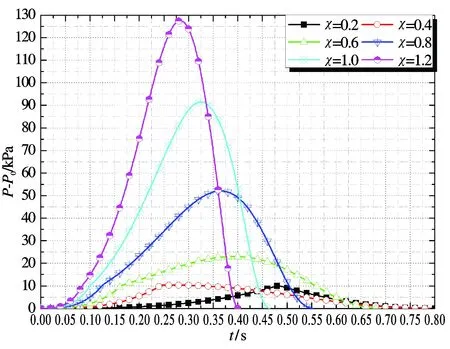
图5 Pstat-P0=10 kPa工况下χ的敏感性分析
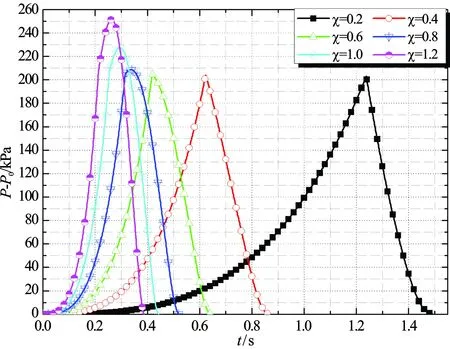
图6 Pstat-P0=200 kPa工况下χ的敏感性分析
参数χ体现的是爆炸中湍流程度的大小。从分析结果可以得到规律:当χ相对偏小时,泄压口的动作时间和超压开始衰减的时间将更接近,并可能在泄压构件动作时压力即开始衰减;当χ相对偏大时,泄压口的动作时间和超压开始衰减的时间将延长,造成泄压后的超压增长。对比结果:对于工况1,χ=0.6吻合程度较高;对于工况7,χ=1.2仍相对较小。说明Pstat-P0相对较低时,对于实际湍动程度给定的χ过大;而Pstat-P0相对较高时,χ又无法达到实际湍动水平。对该现象的解释为:压力的升高会导致传播速度加快,引起湍动程度增大,所以较大的Pstat-P0会引起泄压前维持较高内部压力,进而对应的χ也应增大。NFPA 68中考虑泄压引起的湍流程度时,所给雷诺数的计算模型也考虑到了不同压力下泄放速度不同导致湍动程度不同的关系,并给出Rev∝P1/2的关系,这也印证了该误差分析的合理性。
4 结论
研究可得到如下结论:(1)基于封闭空间的压力增长理论和泄放质量比例的压力衰减假设,建立了泄压条件下气体爆炸超压变化的微分方程模型,并通过固定时间差分离散将其转化为差分方程模型,给出了求解步骤。(2)模型进行代数求解时,时间差分的大小应控制在0.001 s以下以保证求解结果的稳定性。(3)恒定的湍流因子是导致模型误差的主要原因,该模型进行泄压条件下封闭空间的超压计算时,应当考虑通过燃爆指数折算的湍流因子的适用范围。体积为1 m3且泄压面积为0.36 m2空间内的甲烷爆炸,在Pstat-P0处于20~200 kPa之间的误差处于可接受水平。
值得一提的是,湍流程度受到诸多因素的影响,除上文分析的Pstat以外,不同的容器体积、泄压面积、物质种类、初始压力等条件下得到的χ也有所不同,因此模型适用范围也不相同。针对此问题,可以通过后续研究湍流因子在泄压条件下气体爆炸过程中的变化规律进行补充。
[1] 中华人民共和国公安部.建筑设计防火规范:GB 50016—2014[S].北京:中国计划出版社,2015.
[2] Standard on explosion protection by deflagration venting:NFPA 68—2013[S].
[3] Gas explosion venting protective system:BS EN 14994—2007[S].
[4] SWIFT I.Design of deflagration protection systems[J].Journal of Loss Prevention in the Process Industries,1988(1):5-15.
[5] BARTKNECHT W.Explosions-schutz:grundlagen and anwendung[M].Springer-Verlag,Berlin,1993.
[6] ZALOSH R.SFPE handbook of fire protection engineering [M].5th ed. Springer New York Heidelberg Dordrecht London:Society of Fire Protection Engineers,2016.
[7] BRADLEY M,MITCHESON A.The venting of gaseous explosions in spherical vessels[J].Combustion and Flame,1978,32:221-236.
[8] MOLKOV V,KOROLCHENKO A,ALEANDROV S.Venting of deflagrations in buildings and equipment:universal correlation[R].Russian Research Institute for Fire Protection.
[9] HERNANDEZ F,ABDEL-JAWAD M,HAO H.Simplified multiple equations’ inverse problem of vented vessels subjected to internal gas explosion[J].Journal of Loss Prevention in the Process Industries,2015,35:65-79.
[10] CHYZ Y T,MACKIEWICZ M.Simplified function of indoor gas explosion in residential building[J].Fire Safety Journal,2017,87:1-9.
[11] KASMAN RAFIZIANA M D.Vented gas explosion[M].School of Process,Environmental and Materials Engineering,University of Leeds,2008.
(责任编辑马龙)
GasExplosionOverpressureCalculationModelunderDeflagrationVenting
YUAN Dancan, MA Bin, DU Kunze
(TeamofGraduateStudents,TheArmedPoliceAcademy,Langfang,HebeiProvince065000,China)
Based on the theory of pressure increase in enclosed space and the assumed pressure decrease related to the discharge mass ratio, a series of differential equation models are established to interpret the process of gas explosion overpressure under deflagration venting. Through difference discrete within fixed time, the differential equation models are transformed into the difference equation models with solution method proposed. The maximum time element of 0.001 s is suggested through the sensibility analysis of the time difference. Based on methane explosion experiments in a 1m3enclosure with a 0.36 m2vent conducted by Bartknecht, a series of simulations are computed for comparison. Additionally, the scope of application, the causes of error and the mechanism of turbulent factor are analyzed. The results show that when the relative static activation pressure of vent is between 20 to 200 kPa, Bartknecht’s experiments are reliable. When applied to other conditions of deflagration venting, the application range of turbulence factor calculated by the combustion index should be considered.
gas explosion; deflagration venting; overpressure model; turbulent factor
2017-05-21
袁丹灿(1993— ),男,广东汕头人,在读硕士研究生; 马斌(1994— ),男,甘肃兰州人,在读硕士研究生; 杜坤泽(1994— ),男,四川遂宁人,在读硕士研究生。
D631.6
A
1008-2077(2017)10-0014-06

