基于Logistic曲线拟合的全国电气火灾数据分析

艾 鹏，刘义祥，金 静，许 洁，贾 南

(武警学院，河北 廊坊 065000)

●消防理论研究

基于Logistic曲线拟合的全国电气火灾数据分析

艾 鹏，刘义祥，金 静，许 洁，贾 南

(武警学院，河北 廊坊 065000)

我国电气火灾发展形势日益迅猛，给人民生产生活带来巨大损失，因此研究电气火灾的发展规律具有现实意义。采用2004—2012年全国电气火灾数据，利用SPSS软件比较不同曲线的拟合情况，最终确定Logistic逻辑增长模型，通过x2检验，判断出曲线拟合优度，得出电气火灾预测公式，并粗略预测出2016年电气火灾发生比例。此模型的建立，可为消防部门了解电气火灾发展规律提供参考。

电气火灾；Logistic曲线；x2检验；拟合优度

0 引言

随着我国经济建设的大力发展，电能广泛应用于人们生活生产活动中，然而电在造福人类的同时，由于电气安全管理体系和法规建设的不完善，电气操作和使用不当等诸多原因，导致电气火灾隐患及其发生率不断增加，给国民经济和人民生活造成巨大损失。据统计，我国电气火灾年均发生率达26%，年损失约占总损失的36%，而根据一些发达国家的资料显示，英国每年电气火灾占总数的17%以下，而美国和日本更是低于10%。为降低电气火灾发生率，有必要着眼于火灾数据分析和预测，为消防部门认识火灾发展规律、判断火灾形势、制定火灾风险防范和控制计划等提供重要依据[1]。

在我国，利用数据分析预测已经普遍应用于各行各业，其中利用数学模型预测火灾发展也取得了许多成绩，楚志勇[2]通过回归分析的方法利用天津市历年火灾发生率数据建立回归模型对未来的火灾发生率进行了预测，郑双忠[3]通过等维灰色递补GM(1，1)动态预测模型得出某市不同时段(共3个时段)火灾发生率预测值，徐晓楠[4]以及陈俊达[5]等分别采用ARIMA法和指数平滑法两种时间序列方法对火灾发生率进行预测分析，预测结果与实际情况相比都较为精确。Logistic曲线是一种逻辑增长曲线，能较好地反映案例中的增长规律，在消防领域，Logistic主要用于火灾风险评估及火险区域划分等[6]，其大多是基于Logistic二项或多项回归，构建概率模型，得出火灾发生的可能性，但是Logistic曲线本身就具有逻辑增长的特点，可以通过曲线拟合预测火灾起数，不过由于火灾数据具有不完备性、随机性等特点，通过Logistic曲线对火灾数据进行拟合预测并不能应用于长时间段，其适合研究短时间段的火灾发展规律。采用近10年全国电气火灾数据，比较各种预测模型，预测电气火灾的发展趋势，希望能为今后的消防工作提供参考。

1 Logistics模型的预测方法

Logistic曲线方程是生物数学家P.F.Verhulst于1938年为了研究人口增长过程而导出的，其特点是在一定程度上稳定环境因素条件下，开始增长缓慢，而在以后的某一范围内迅速增长，达到某限度后，增长又缓慢下来。曲线略呈拉长的“S”型[7]。其模型公式为：

Logistic曲线有3个关键点，用于研究曲线所代表的现实意义。求Logistic曲线方程的一阶导数，可以得到Logistic增长或生长过程的速度函数：

求Logistic生长速度函数的二阶导数，令其等于0，得：

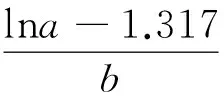
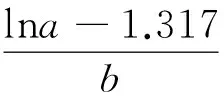
2 实例分析

2.1 数据预处理

数据来自中国消防年鉴(2004—2012年)，为消除属性的量纲影响，进行去量纲化处理，求得每年的火灾总数与电气火灾总数的比值作为处理后的数据进行统计分析，如表1所示。

表1 全国电气火灾数据统计情况

2.2 比较不同曲线的拟合情况

为了找出最佳的拟合曲线，选定可决系数R2作为评价参数比较Logistic曲线与其他曲线，可决系数能够反映曲线对样本观测值的拟合程度。通过SPSS中的曲线估计，得到一次、二次、三次、衰减指数拟合曲线的可决系数R2，如表2所示。

表2 不同拟合曲线的拟合优度

以全国电气火灾所占百分比为纵坐标，为了使数据简单，便于计算，取横坐标数值=当时年份-2000年，通过SPSS中的曲线估计得到图1。根据可决系数值以及图1所示，除直线外，其余曲线拟合都具有较高的精确度，但还需结合Logistic曲线的拟合情况进行比较。

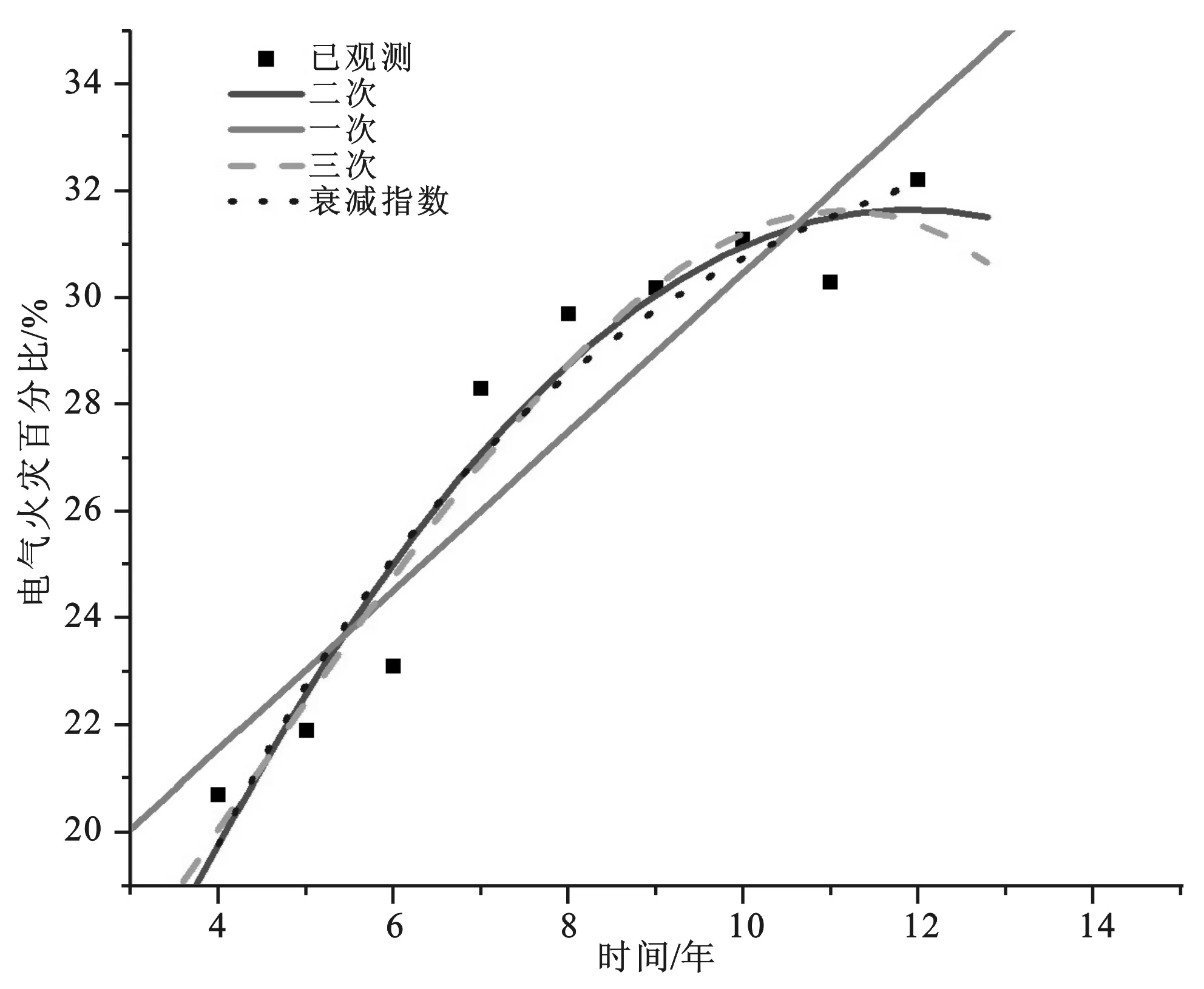
图1 对全国电气火灾发生率拟合的曲线

2.3 Logistic曲线拟合

2.3.1 参数初始值估计

为了能够使曲线的拟合效果更佳，决定探寻Logistic的拟合优度，主要采用SPSS软件中的非线性拟合方法。首先应确定参数的初始值，以保证其后的迭代计算正常、迅速收敛，同时应避免参数初始值过小，计算时无法再收敛精确。由于Logistic曲线不可化为简单的线性表达式，所以初始值的求解分为以下步骤进行：第一步求参数K，K值一般用三点法估计，公式[9]为：

式中，(t1，N1)、(t2，N2)、(t3，N3)分别表示实测数据序列的始点、中点、终点。其中K值采用三点法对其进行初始值的确定，这样选取的点为2004、2008、2012年所对应的点，并将所对应的数据代入式(3)，解得K=32.80。

第二步估计参数a和b，由于式(1)具有非线性，利用其构造的模型为非线性模型，需转化为线性模型后通过最小二乘法求解，式(1)经线性变化为：

z与t为线性回归关系，利用Excel，由最小二乘法估计出参数a=e1.17，b=0.40[10]。

2.3.2 非线性拟合

非线性拟合的方法是不断地将“参数估计值(参数的初始估计值)”代入“损失函数”求解，而“损失函数”采用的是“残差平方和”最小，在迭代m次后，残差平方和达到最小值，此时找到最优解，迭代终止。具体操作步骤：在SPSS中进入分析-回归-非曲线拟合[11]，导入因变量电气火灾所占百分比，导入模型表达式K/(1+EXP(r-b*t))，其中r=lna，导入计算后的参数估计值K=32.80，b=0.40，r=1.17，保存预测值、残差，选项中估计方法选择序列二次编程，经过迭代计算后得出如表3所示的结果。由表中数据可知经过7次迭代计算后数据保持不变，最后的参数值K=33.049，r=1.099，b=0.374。同时通过SPSS得到Logistic的拟合曲线如图2所示。

从图2可以看出，Logistic模型对表1的电气火灾统计数据具有较好的拟合效果，根据SPSS得到的输出结果，可决系数R2=0.939，具有非常高的拟合度，与图1相比更能反映数据的逻辑增长特征；与表2中各个曲线的可决系数进行对比发现Logistic的数值更能接近1，因此Logistic曲线更能反映出数据特征，最后的曲线表达式为：

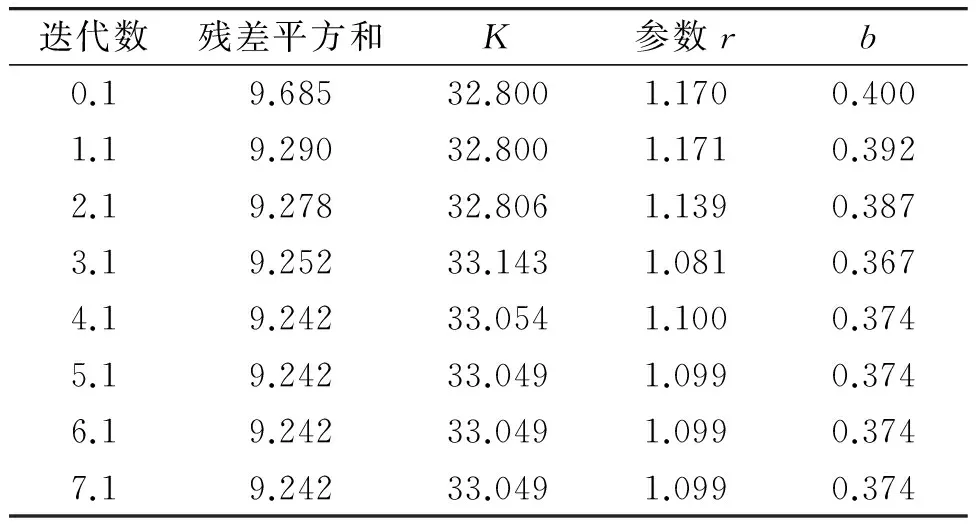
表3 迭代历史记录

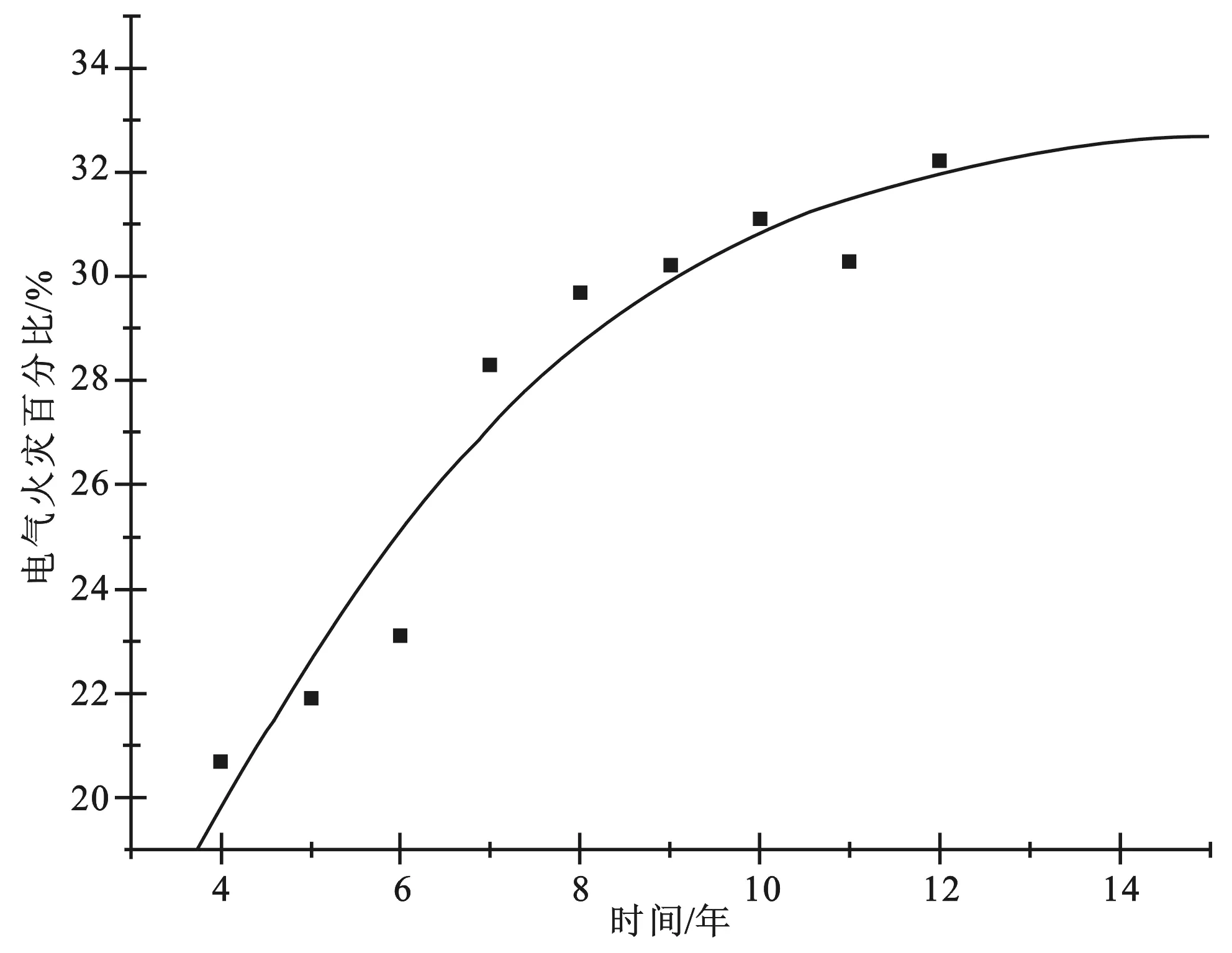
图2 用Logistic对全国电气火灾 发生率拟合的曲线

式(6)反映了全国电气火灾2004—2012年的逻辑增长情况，K值为33.049，代表电气火灾发生率所能达到的理论最高值，也是当前环境因素条件下的理论饱和值，当电气火灾发生率达到理论最高值时，之后的发展会因环境因素(社会经济状况、群众防火安全意识等)的改变而出现明显的改变。根据公式可以对未来的全国电气火灾发生率进行预测，经计算可以得出2013、2014、2015、2016年的电气火灾起数所占百分比预测值为32.29%、32.52%、32.68%、32.80%。

2.3.3 求取关键点

为研究实例的逻辑增长规律，分析曲线不同时段的增长特性，探求电气火灾发生率的现实情况，根据Logistic曲线的特点，求取式(6)的3个关键点，由式(2)可得Logistic曲线的3个关键点的横坐标为t1=-0.59，t2=2.75，t3=6.53。因为文中数据是取自2004—2012年的，是基于某一时段的数据分析，时间作为因变量，且数据自变量包含的时间范围较短，所以Logistic曲线会在x轴上有偏移，出现t值为负的情况，表示1999年之前的情况，这里不做分析。根据计算出的3个关键点可知，全国电气火灾发生率快增期为2004—2007年，缓增期为2007年—∞。

2.3.4x2检验

由于Logistic曲线回归方程除含有回归参数a和b，还含有常量K，为了更精准地验证曲线的拟合优度，利用实际值和预测值，运用x2测验，确定曲线的拟合优度，以验证公式的合理性[8]。

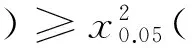
表4 全国电气火灾所占比例的实际值与预测值

3 结论

通过R2值的比较与x2检验发现Logistic曲线的拟合效果更好，因此针对实例确定最终的推导公式(6)，并对2013、2014、2015、2016年的火灾进行预测，得出结果为2013、2014、2015作为检验年份预测值为32.29%、32.52%、32.68%，与实际值29.7%、27.4%、30.2%基本相符，2016的电气火灾发生比率预测值为32.80%。分析我国电气火灾发生率的增长规律发现我国电气火灾仍处于持续高发状态，2004—2007年是我国电气火灾的高速增长期，特点为电气火灾发生基数不大，但发生比率在逐年高速增长。2007年开始是我国电气火灾的缓增期，特点为电气火灾发生比率仍逐年增加，但增加的速度明显减小，电气火灾的发展逐渐进入稳定期。

[1] 兰丽娜.我国电气火灾发展的特点分析及其综合防治对策研究[J].科技风,2011(8):251-252.

[2] 楚志勇.基于回归分析方法的城市火灾预测:以天津市为例[J].安全与环境工程,2011,18(3):90-92.

[3] 郑双忠.基于灰色系统理论的城市火灾预测分析[J].数学的实践与认识,2005,35(1):72-76.

[4] 徐晓楠,张晓珺,施照成.基于北京市火灾统计数据的时间序列分析[J].安全与环境学报，2014,14(1):73-77.

[5] 陈俊达,李晓宏,李佳乐,等.基于时间序列分析的火灾分析与预测[J].科学之友,2011(11):42-43.

[6] 王卫国,潘竟虎,李俊峰.基于空间Logistic的山西省火灾风险评价与火险区划[J].草业科学,2016,33(4):635-644.

[7] 胡喜生,范海兰,宋萍,等.改进Logistic模型在城市人口预测中的应用[J].北华大学学报(自然)，2008,9(4):370-373.

[8] 崔党群.Logistic曲线方程的解析与拟合优度测验[J].数理统计与管理,2005,24(1):112-115.

[9] 殷祚云.Logistic曲线拟合方法研究[J].数理统计与管理,2002,21(1):41-46.

[10] 张润莲,苏国强,杨建华,等.基于Logistic模型的火灾损失研究文献分析[J].内江科技,2013,34(11):107-108.

[11] 董江水.应用SPSS软件拟合Logistic曲线研究[J].金陵科技学院学报,2007,23(1):21-24.

(责任编辑马龙)

AnalysisofNationalElectricFireDataBasedonLogisticCurveFitting

AI Peng, LIU Yixiang, JIN Jing, XU Jie, JIA Nan

(TheArmedPoliceAcademy,Langfang,HebeiProvince065000,China)

The number of China’s electrical fire is increasing rapidly, bringing great losses to people’s production and life, so to study the law of electrical fire occurrence is of great significance. In this paper, the SPSS software is used to compare the fitting of different curves based on the data of national electrical fires from 2004 to 2012. Finally, a Logistic logic growth model is determined. The goodness of curve fitting is obtained by Chi-square test, and a prediction formula of electrical fires is obtained, which can roughly forecast the proportion of electrical fires in 2016. This model provides a reference for the fire department to understand the law of electrical fire occurrence.

electrical fire; Logistic curve; Chi-square test; goodness of fitting

2017-04-10

河北省统计科学研究计划项目“大数据背景下城市火灾预测与可视化研究”(2016HY11)阶段性成果； 河北省科技计划项目“面向大数据的城市火灾预测关键技术研究”(16215416)阶段性成果

艾鹏(1993— )，男，辽宁锦州人，武警学院在读硕士研究生； 刘义祥(1970— )，男，河北南皮人，教授； 金静(1986— )，女，安徽萧县人，讲师，博士； 许洁(1983— )，女，河北廊坊人，讲师； 贾南(1987— )，男，河北廊坊人，讲师。

D631.6

A

1008-2077(2017)10-0005-04