构架式可展天线机构自由度分析
——拆杆等效法
许允斗, 刘文兰, 陈亮亮, 姚建涛, 赵永生,*, 朱佳龙
1.燕山大学 河北省并联机器人与机电系统实验室, 秦皇岛 066004 2.燕山大学 先进锻压成型技术与科学教育部重点实验室, 秦皇岛 066004 3.中国空间技术研究院 西安分院, 西安 710100
构架式可展天线机构自由度分析
——拆杆等效法
许允斗1,2, 刘文兰1, 陈亮亮1, 姚建涛1,2, 赵永生1,2,*, 朱佳龙3
1.燕山大学 河北省并联机器人与机电系统实验室, 秦皇岛 066004 2.燕山大学 先进锻压成型技术与科学教育部重点实验室, 秦皇岛 066004 3.中国空间技术研究院 西安分院, 西安 710100
针对四面体构架式可展天线机构的多环耦合特性,提出了一种空间多环耦合机构的自由度分析方法——拆杆等效法。首先拆除四面体基本可展单元机构的耦合约束链,将剩余部分视为一个并联机构,然后应用螺旋理论分析各输出节点的自由度数目及性质,进而构造各输出节点与定节点之间的等效串联运动链,最后复原拆除的耦合约束链得到四面体基本可展单元的等效机构,应用修正的G-K公式计算等效机构的自由度数目,并基于反螺旋理论分析等效机构的自由度性质,从而获得四面体基本可展单元的运动特性。根据四面体基本可展单元的等效机构及其组合方式对最小组合单元及大尺寸构架式可展天线机构的结构进行了化简,并根据其几何特征约束方程推导了最小组合单元及大尺寸构架式可展天线机构的自由度。建立了由27个四面体基本可展单元组成的构架式可展天线机构的仿真模型,对该机构的自由度进行了验证,结果表明提出的拆杆等效法求得的自由度正确,为进一步分析此类天线机构的运动学和动力学奠定了基础,同时为其他类型的空间多环耦合机构的自由度分析提供了一种新的思路。
拆杆等效法; 四面体单元; 可展天线; 自由度; 螺旋理论
空间可展开天线已在卫星通信、遥感测量、空间探测及军事侦察等领域得到了广泛应用。目前,可展开天线的种类多种多样,其中,构架式可展天线整个网面靠桁架支撑,不仅刚度大且易于保证形面精度,其支撑机构由若干个基本可展单元组成,稳定性好、折叠比大,因此,构架式可展天线是目前及未来较长时间内大型可展天线的主要发展对象之一。
构架式可展天线在国内外已经获得了多次在轨应用,例如,在俄罗斯“联盟号”飞船[1]、日本ETS-VIII卫星[2]以及中国的HJ-1-C卫星SAR天线[3]上,等等。随着构架式可展天线的多次成功应用,此种天线的研究受到了越来越多学者的关注。Jin等[4]应用多柔体动力学仿真软件对一种构架式可展天线的展开过程进行了分析,关富玲等[5]提出了一种程序化设计四面体构架式可展天线机构的方法,陈务军等[6]通过推导两端带扭簧的杆件宏单元的缩减线弹性刚度矩阵和一致质量矩阵分析了扭簧刚度对扭簧驱动的构架式可展天线结构的影响,文献[7-8]给出了带弹簧节点的构架式天线结构详细的设计方案,Xu和Guan[9]综合考虑四面体构架式可展天线机构的机械性能和电气性能提出了一种结构-电气综合设计方法,杨玉龙等[10]从工程角度以结构设计的技术指标和全部构件集合为系统要素,基于结构解析模型法设计了一个四面体可展桁架抛物面天线,文献[11]提出了一种利用伸缩杆驱动的六棱柱展开单元及其构成的大型构架式切割抛物面天线,黄志荣等[12]基于驱动部件的失效模式开展了面向可靠性的四面体构架式可展天线机构驱动部件的优化设计,后来其又对偏馈式四面体构架可展天线机构进行了系统的构型设计和展开协调性研究[13],张海波等[14]以弦杆夹角的均匀性和最小均方根误差为优化准则提出了确定四面体构架式可展抛物面天线上弦节点位置的三种映射方法:平面桁架垂直投影映射、中轴线弧等长映射和弦长协调变化映射,此外,文献[15-18]也对构架式可展天线的结构设计、展开稳定性等展开了相关研究。
上述这些文献都是针对构架式可展天线的结构设计和控制展开的研究,目前鲜有关于构架式可展天线支撑机构(以下简称为构架式可展天线机构)自由度分析的文献报道,而机构自由度的分析是对一个机构最基本的认识。构架式可展天线机构由多个基本可展单元通过一定的机构学原理连接而成,其基本可展单元本身就属于空间多环耦合机构,因此,这类天线机构的结构比一般的串联、并联及串并混联机构要复杂得多,传统的机构自由度分析方法[19-24]和单个多环耦合机构的自由度分析方法[25-27]已不再适用于此类构架式可展天线机构。鉴于上述原因,本文提出一种拆杆等效法分析四面体构架式可展天线机构的自由度。
1 拆杆等效法介绍
鉴于空间多环耦合机构可以看做是在并联机构的基础上添加一定数量的耦合约束链构成的,本文提出一种拆杆等效法分析此类机构的自由度。该方法的主要思想是先将机构的耦合约束链拆除得到基本并联机构,然后基于螺旋理论分析基本并联机构动平台的自由度数目及性质,进而构建并联机构动平台与基座之间的等效串联运动链,再次复原拆除的耦合约束链得到整个多环耦合机构的等效机构,最后通过分析等效机构的自由度获知原多环耦合机构的自由度。其求解步骤可概括为:① 拆杆,得到基本并联机构;② 基于螺旋理论分析并联机构的自由度;③ 根据并联机构的自由度数目及性质建立等效串联运动链;④ 复原拆杆,建立原空间多环耦合机构的等效机构,分析等效机构的自由度。
其中,从多环耦合机构中合理拆分基本并联机构和构建整个机构的等效机构是该方法的关键。需要注意的是:① 为了复原拆杆后得到构型简单的等效机构,在选择基本并联机构时以与耦合约束链两端相连的杆件之一作为并联机构的动平台;② 因在原位置复原拆除的耦合约束链,故需分别以与耦合约束链两端连接的杆件为并联机构的动平台分析其自由度并构建其与基座之间的等效串联运动链。
本文以四面体可展天线机构为例应用拆杆等效法分析此类空间多环耦合机构的自由度。
2 四面体可展天线机构的自由度分析
2.1 基本可展单元的结构及自由度分析
四面体可展天线机构的基本可展单元由4个节点、9根连杆和15个转动副组成,如图1所示。为方便分析,记四面体基本可展单元顶端的1个节点和底面的3个节点分别为H、A、B、C,15个转动副的中心分别为点R1~R15,连杆R10R11、R12R13、R14R15的轴线延长线相交于点P,四面体底面三角形ABC的外心为点O。连杆R1R2和R2R3等长,连杆R4R5和R5R6等长,连杆R7R8和R8R9等长,连杆R10R11、R12R13、R14R15等长,15个转动副的方向矢量S1~S15满足的几何关系为:S1∥S2∥S3⊥平面R1R2R3,S4∥S5∥S6⊥平面R4R5R6,S7∥S8∥S9⊥平面R7R8R9,S10∥S11⊥平面AOP,S12∥S13⊥平面COP,S14∥S15⊥平面BOP,且节点H上的三个转动副共面。
该四面体基本可展单元属于空间多环耦合机构,根据本文提出的拆杆等效法选取节点B和C之间的R7R8R9运动链为耦合约束链,以节点A为基座,分别以节点B和C为并联机构的动平台分析其相对于基座的自由度数目和性质。
首先,拆除节点B和C之间的R7R8R9耦合约束链,将四面体基本可展单元的剩余部分视做以节点A为基座,节点B为动平台,含两个支撑分支的并联机构,如图2所示,其中,一个分支为R1R2R3串联运动链,另一个分支为含闭环子链的(R4R5R6R12R13R11R10)-R15R14运动链。
其次,基于螺旋理论分析图2所示的基本并联机构的自由度。在基座A处建立参考坐标系A-XYZ,其中X轴沿节点B、A的连线方向,Y轴位于平面ABC且与节点B、A的连线垂直,则Z轴恰好与四面体单元底面的法线OP平行,如图2 所示。四面体可展单元在收拢/展开过程中任意位形下其连杆R1R2和R2R3处于半折叠状态(即两杆不共轴),连杆R4R5和R5R6、R7R8和R8R9亦然,则在四面体可展单元收拢/展开过程中的任意位形下,图2所示并联机构的分支1的运动螺旋系在参考坐标系A-XYZ下可表示为
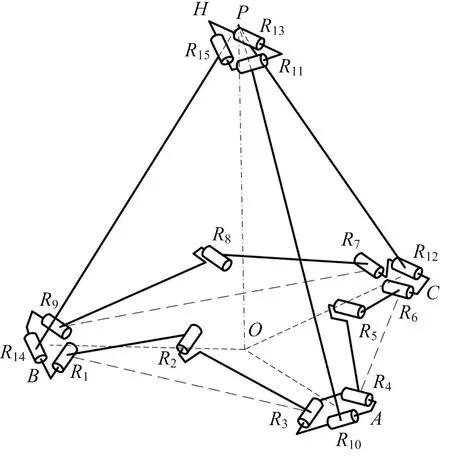
图1 四面体基本可展单元结构简图 Fig.1 Schematic diagram of deployable tetrahedralelement
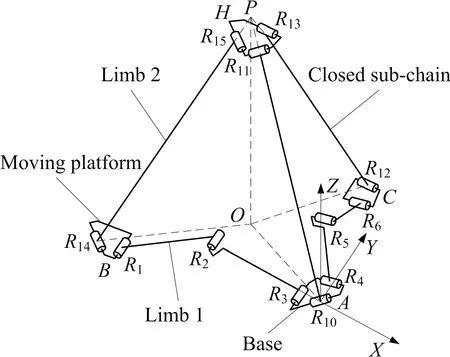
图2 拆杆后的基本并联机构简图Fig.2 Schematic diagram of parallel mechanism with one coupled chain being removed
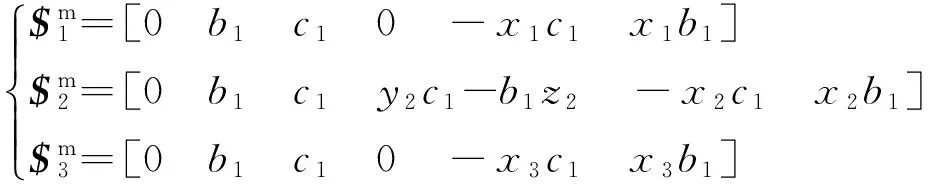
(1)
式中:[0b1c1]为分支1中转动副的方向矢量;[x10 0]、[x2y2z2]、[x30 0]分别为转动副中心点R1、R2、R3的坐标。
求式(1)所示运动螺旋系的反螺旋可得分支1提供给动平台B的约束力螺旋系为
(2)
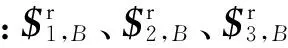
在分析分支2提供给动平台B的约束作用之前先分析与分支2的闭环子链等效的广义运动副。将闭环子链R10R4R5R6R12R13R11视作以节点H为动平台、节点A为基座,含分支R10R11和分支R4R5R6R12R13的并联机构,则分支R10R11的运动螺旋系在坐标系A-XYZ下可表示为
(3)
式中:[a4b40]为连杆R10R11两端转动副的方向矢量;[x11y11z]为转动副中心点R11的坐标。
根据反螺旋理论可得分支R10R11提供给节点H的约束力螺旋系为
(4)

同理,分支R4R5R6R12R13的运动螺旋系在坐标系A-XYZ下可表示为
(5)
式中:[a2b2c2]和[a5b50]分别为运动链R4R5R6中转动副和连杆R12R13两端转动副的方向矢量;[x4y40]、[x5y5z5]、[x6y60]、[x12y120]和[x13y13z]分别为转动副中心点R4、R5、R6、R12和R13的坐标。
求式(5)所示螺旋系的反螺旋可得分支R4R5R6R12R13提供给节点H的约束力螺旋为
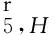
(6)
式(6)表示与运动链R4R5R6中转动副和连杆R12R13两端转动副的轴线均垂直的约束力偶。
则求式(4)和式(6)所示约束力螺旋的并集可得在闭环子链中节点H受到的约束力螺旋系,从而根据反螺旋理论可得节点H的运动螺旋为

(7)

分支P0R15R14提供给动平台B的约束力螺旋系在坐标系A-XYZ下可表示为

图3 分支2的等效分支Fig.3 Equivalent mechanism of limb 2
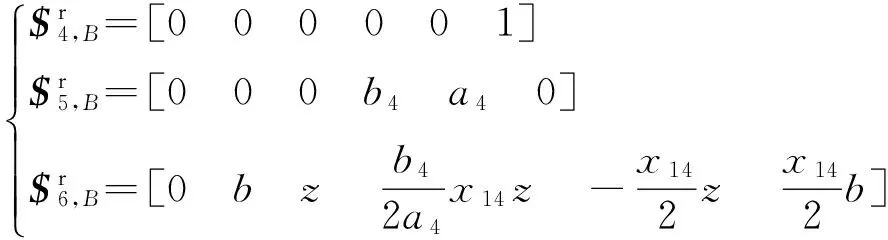
(8)
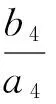
则式(2)和式(8)所示约束力螺旋系的并集即为动平台B受到的约束力螺旋系,求该约束力螺旋系的反螺旋可得节点B相对于节点A的运动螺旋为
(9)
式(9)表示沿X轴的移动,即在四面体可展单元收拢/展开过程中任意位形下拆除耦合约束链R7R8R9得到的并联机构中节点B相对于节点A具有1个沿A、B连线方向的移动自由度。
同理,以节点C为并联机构的动平台,可得节点C相对于节点A也具有1个沿A、C连线方向的移动自由度。因此,在拆除耦合约束链R7R8R9的机构中,节点B和C与节点A之间的等效串联运动链均为1个移动副,记节点B和C与节点A通过移动副相连的接触点分别为P1和P2。
最后,在节点B和C之间复原拆除的R7R8R9约束链,并结合节点B(C)与节点A之间的等效串联运动链可构建图1所示的处于收拢/展开过程中的四面体基本可展单元的等效机构,如图4所示。

图4 四面体基本可展单元的等效机构 Fig.4 Equivalent mechanism of deployable tetrahedralelement
显然,图4所示的单闭环机构中,与三个转动副的轴线垂直的2个约束力偶为该机构的公共约束,该机构中不存在冗余约束和局部自由度,则根据修正的G-K公式可得图4所示等效机构的自由度为
4×(5-5-1)+5=1
(10)
式中:M为机构的自由度数目;d为机构的阶数,且d=6-λ,λ为机构的公共约束数;n为含机架的构件数;g为机构中运动副的数目;fi为第i个运动副的自由度数目;v为除公共约束后冗余约束的数目;ξ为机构中存在的局部自由度数。
式(10)表明图4所示的等效机构只有1个自由度,且在该机构运动过程中节点B和节点C相对于节点A只发生移动运动。为便于分析节点B和C向节点A移动的过程中节点B和C之间的相对运动,将节点B视为定节点,节点C视为动节点,根据运动螺旋和约束力螺旋之间的反螺旋关系可知P1P2运动链提供给节点C一个垂直平面ABC的约束力和空间的三个约束力偶,R7R8R9运动链提供给节点C一个沿该链中转动副轴线的约束力和两个与该链中转动副轴线垂直的约束力偶,则节点C共受到2个约束力和5个约束力偶,限制了节点C的2个移动和3个转动自由度,根据2个约束力的方位可知节点C相对于节点B具有1个沿B、C连线方向的移动运动,因此,节点B与C之间的R7R8R9运动链与一个轴线沿B、C连线方向的移动副等效,记节点B和C通过移动副相连的接触点为P3,则图4所示的等效机构可进一步简化为图5所示的机构。
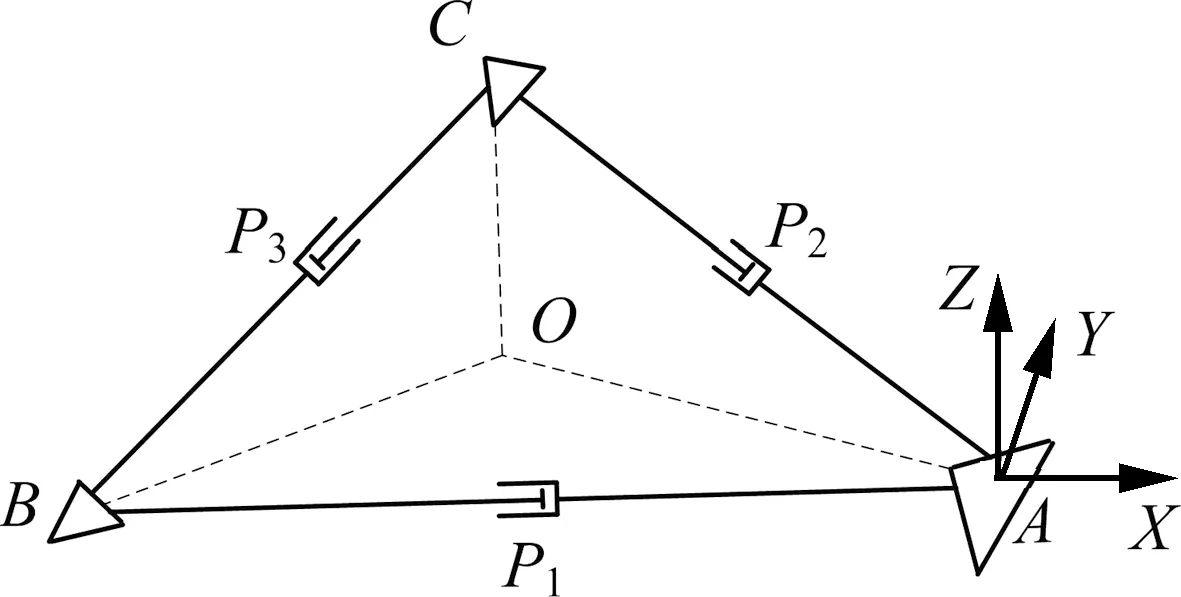
图5 四面体基本可展单元的最简等效机构 Fig.5 Simplest equivalent mechanism of deployabletetrahedral element
综上,图1所示的四面体基本可展单元在收拢/展开过程中始终具有1个自由度,任选1个转动副添加驱动,若顶节点H固定,则在驱动作用下,节点A、B、C始终保持各自的姿态不变分别沿直线AO、BO、CO同步远离或靠近点O,即在四面体基本可展单元的收拢/展开过程中,其底面三角形ABC同比例缩小或放大。

(11)

(12)

运动链R4R5R6中间转动副运动螺旋的改变未影响分支2提供给动平台B的约束力螺旋系,因此,四面体基本可展单元在完全展开状态,其动平台B受到的约束力螺旋系为式(2)、式(8)和式(12)所示约束螺旋的并集,该约束力螺旋系的最大线性无关数为6,限制了动平台B所有的自由度。
因此,四面体基本可展单元机构在完全展开状态自由度为零,则由其组成的最小组合单元及大型构架式可展天线机构在完全展开状态的自由度也为零。从机构学角度来说四面体基本可展单元及其组成的大型机构的完全展开状态即为其在整个工作空间内的边界奇异位形,机构处于极限点时不能再继续运动。故仅分析四面体基本可展单元组成的最小组合单元及大型构架式可展天线机构在收拢/展开过程中任意位形下的自由度。
2.2 最小组合单元的结构及自由度分析
四面体可展天线机构的最小组合单元由3个基本可展单元共用1个底面节点且基本可展单元彼此之间通过三个转动副构成的串联约束链连接而成,如图6所示。每条三转动副串联链中的两根连杆等长,且在每个四面体基本可展单元中,底面节点与顶节点之间的连杆等长。
根据前述四面体基本可展单元在收拢/展开过程中任意位形下的等效机构及基本可展单元间的连接方式易得四面体可展天线机构的最小组合单元的等效机构如图7所示。
假设图7中节点A为定节点,且断开节点B与G之间的三转动副串联约束链,在四面体基本可展单元H-ABC的节点B与A之间的移动副上添加驱动,则根据单个基本可展单元的自由度数目及性质可知在驱动作用下节点B、C、D、E、F、G会同步移动到B′、C′、D′、E′、F′、G′位置,如图8所示。
根据相似三角形的性质可得
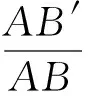
(13)
即
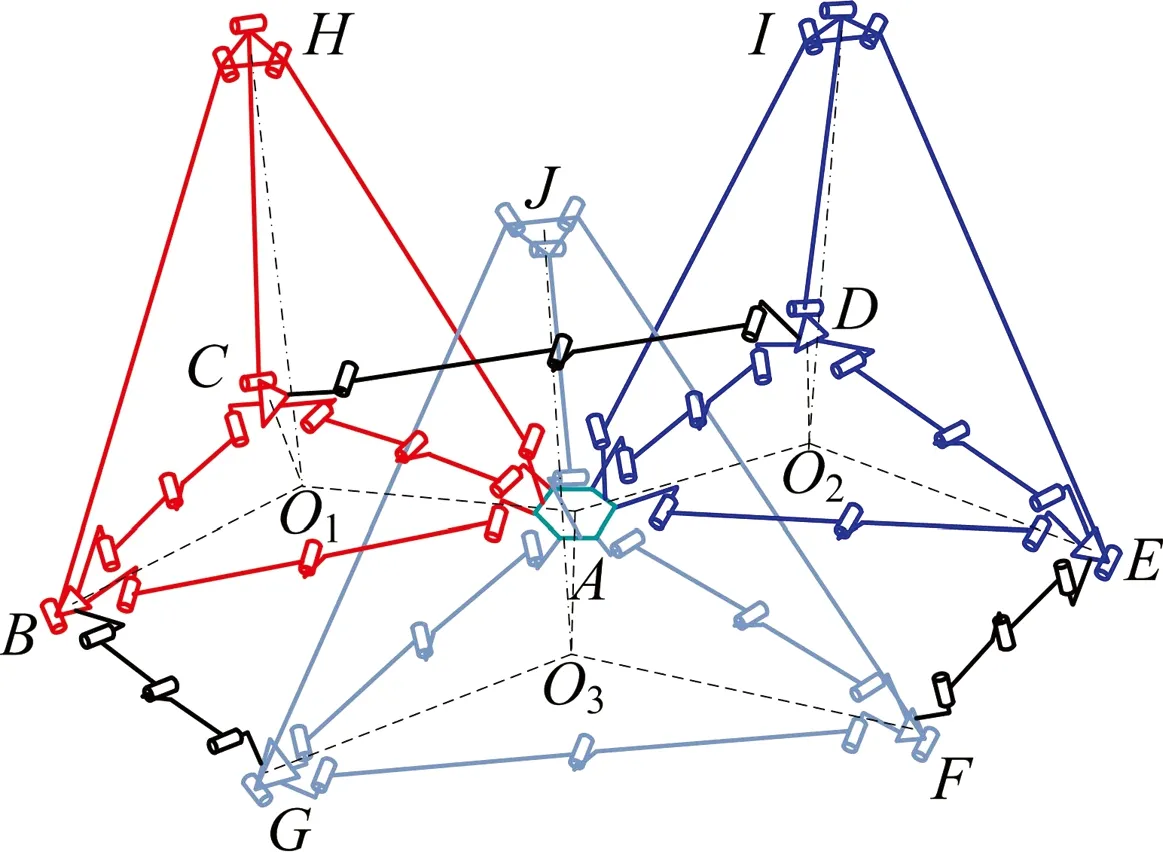
图6 最小组合单元结构简图Fig.6 Schematic diagram of the minimum composite unit
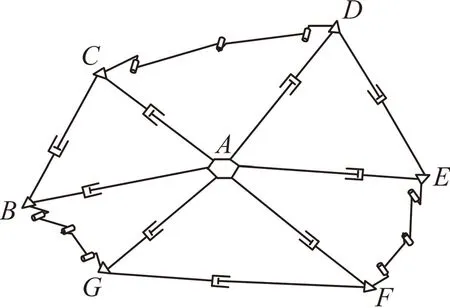
图7 最小组合单元的等效机构 Fig.7 Equivalent mechanism of the minimum compositeunit

图8 图7所示机构运动后的位形Fig.8 Configuration of mechanism shown in Fig.7 after movement
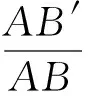
(14)
式(14)表明当节点B和G之间无约束链时,在节点B和A之间移动副上添加的驱动作用下,节点B和G分别沿直线BA和GA同步向节点A移动,而根据本文2.1节的分析可知若复原节点B和G之间的三转动副串联约束链同样能保证等式(14)成立,因此,图7所示的等效机构的自由度为1,即四面体可展天线机构的最小组合单元在收拢/展开过程中具有1个自由度。
2.3 大型四面体可展天线机构的结构及自由度分析
大型四面体构架式可展天线的支撑机构由多个四面体基本可展单元彼此之间共用1个底面节点组成。鉴于每个四面体单元的结构均如图1所示,在下文中只用简单的线条表示四面体,不再给出所有转动副的简图,图9所示为由12个四面体基本可展单元两两之间共用1个底面节点组成的构架式可展天线机构的俯视图,其中周边节点M1与M2、M2与M3、M5与M6、M6与M7、M9与M10、M10与M11之间仍通过三转动副串联约束链连接。
根据四面体基本可展单元在收拢/展开过程中任意位形下的等效机构及基本单元间的连接方式可得图9所示构架式可展天线机构在收拢/展开过程中的等效机构如图10所示。
假设图10所示机构中的12个四面体单元的运动相互独立,则根据本文2.1节对四面体基本可展单元自由度的分析可知每个四面体单元在运动过程中其底面三角形同比例缩小/放大,即存在以下几何关系:

图9 含12个四面体单元的构架式可展天线机构的俯视图Fig.9 Top view of deployable truss-antenna mechanism assembled by 12 tetrahedral elements
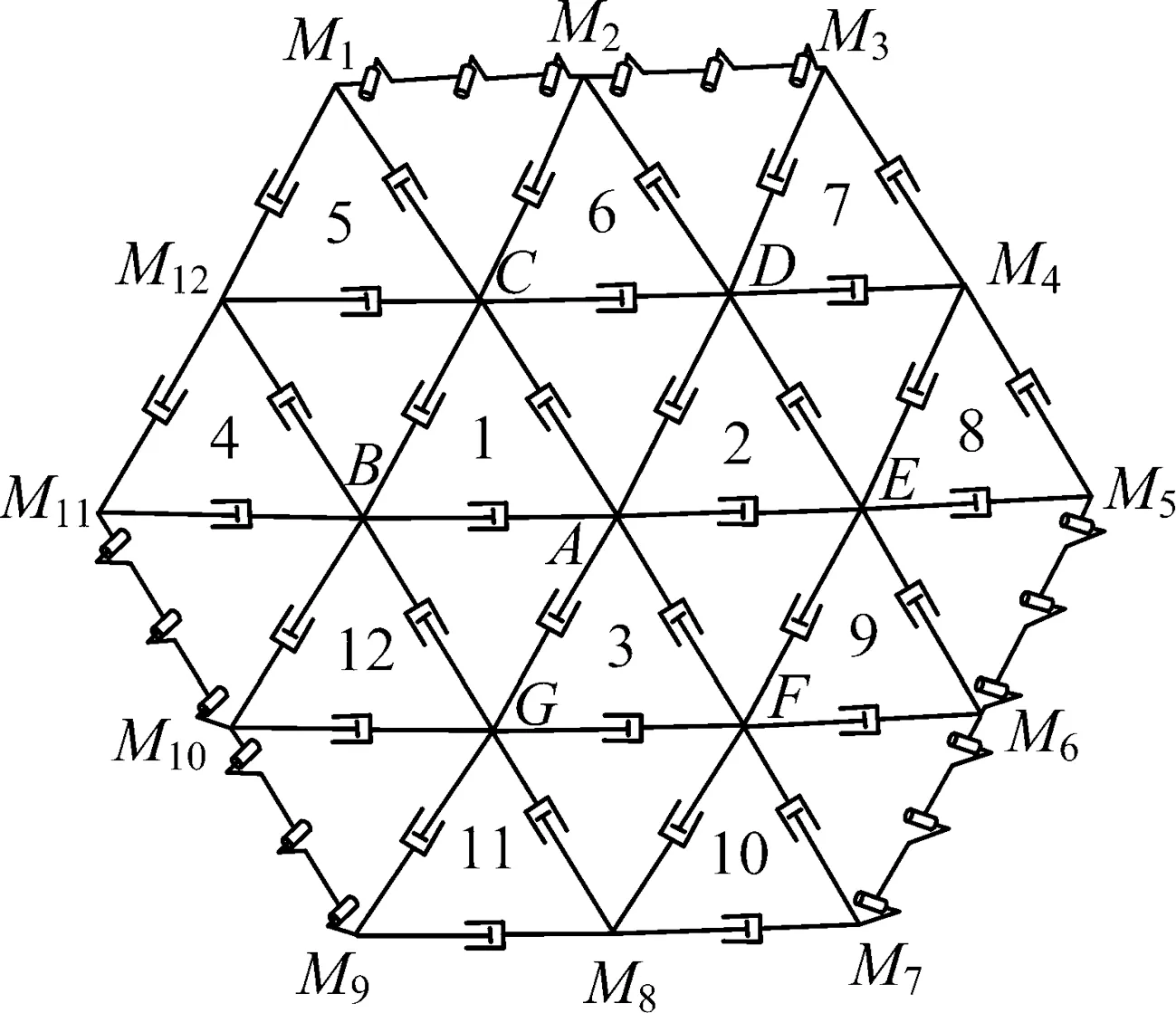
图10 图9所示构架式可展天线机构的等效机构Fig.10 Equivalent mechanism of deployable truss-antenna mechanism shown in Fig.9
(15)
式中:A′B′、A′C′和B′C′分别为四面体单元ABC在独立收拢/展开过程中底面节点A与B、A与C、B与C之间的距离,是随时间变化的量;AB、AC、BC分别为四面体单元ABC在初始状态下底面节点A与B、A与C、B与C之间的距离,是常量;λ1为四面体单元ABC在收拢/展开过程中其底面节点两两之间的距离相对于初始距离的变化系数,是个变量;与λ1的定义类似,λ2~λ12分别为其他11个四面体单元在独立收拢/展开过程中底面节点两两之间的距离相对于相应初始距离的变化系数。
此外,从图9和图10可以看到第1~12个四面体基本可展单元两两之间共用1个节点组成构架式可展天线机构的过程中自动构成了闭环机构BCM12、ACD、EDM4、AEF、ABG及GFM8,假设这6个闭环机构的运动也相互独立,则这6个闭环机构在运动过程中存在以下几何关系:
(16)
式中:λ13~λ18分别为闭环机构BCM12、ACD、EDM4、AEF、ABG及GFM8在独立收拢/展开过程中其节点两两之间的距离相对于相应初始距离的变化系数,与λ1的定义类似。
当上述12个四面体单元机构和6个闭环机构的运动相互制约时,将式(16)代入式(15)可得
λ1=λ2=…=λ18
(17)
式(17)表明所有四面体单元在运动过程中底面相邻两节点间距离相对于其初始距离的变化系数相等,则仅在单个驱动作用下图10所示机构就能实现整体缩小/放大。因此,图9所示的由12个四面体基本可展单元组成的天线机构在收拢/展开过程中具有1个自由度,若固定底面中心节点A,则所有四面体同步向节点A靠拢,且在运动过程中各节点姿态始终保持不变。
同理可得由n(n>12)个四面体基本可展单元两两共用1个底面节点组成的大型构架式可展天线机构在收拢/展开过程中具有1个自由度,在完全展开状态(即边界奇异位形处)机构自由度减少为零。
3 仿真验证
根据前述分析可知由多个四面体基本可展单元组成的大型构架式可展天线机构在收拢/展开过程中只具有1个自由度,即在机构收拢/展开的过程中所有节点只发生相对移动,其姿态始终保持初始位形下的姿态不变。在这里以图11所示的由27个四面体基本可展单元组成的球面构架式可展天线的支撑机构为例验证前述自由度分析的正确性。
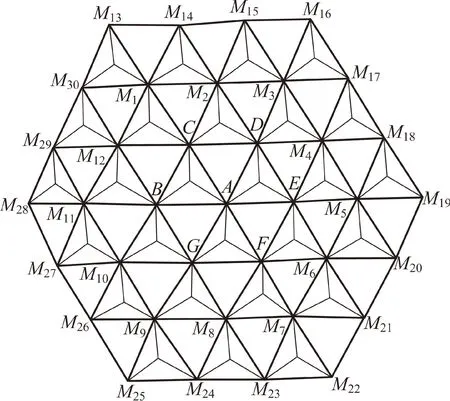
图11 含27个四面体单元的构架式可展天线机构俯视图Fig.11 Top view of deployable truss-antenna mechanism assembled by 27 tetrahedral elements
图11所示构架式可展天线机构在完全展开状态的三维模型如图12所示,该位形下27个四面体单元底面的节点位于球面上,即底面各节点姿态不相同。一般来说机构处于奇异位形时需靠冗余驱动或附加外力避开该位形后才恢复原有的自由度,因此,添加多个驱动使图12所示可展天线机构避开其边界奇异位形(即完全展开状态)后,仅在连接节点A和B的三转动副串联约束链的中间转动副上添加驱动,使该转动副每秒转动0.5°,则所有四面体单元在该驱动作用下同步向中心节点A收拢,图13和图14分别为该天线机构的半收拢状态和收拢末态。需要说明的是任选该机构的其他转动副添加驱动,均能达到图14所示的收拢末态。
在图11所示机构中选取四面体单元底面三角形M1M2M14,已知在该机构完全展开状态节点M1与M2、M2与M14、M1与M14之间的距离为:M1M2=0.353 m,M2M14=0.395 m,M1M14=0.377 m,测得在机构收拢过程中节点M1与M2、

图12 完全展开状态的三维模型Fig.12 3D model of antenna in fully expanded state

图13 中间状态的仿真模型Fig.13 Simulation model of antenna in its middle state

图14 收拢末态的仿真模型Fig.14 Simulation model of antenna in its folded state
M2与M14、M1与M14之间的距离变化曲线如图15 所示。
令
(18)
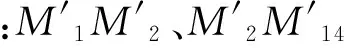
由图15和节点M1与M2、M2与M14、M1与M14之间的初始距离可得
λ1,2=λ2,14=λ1,14=λ0
(19)

图15 三角形M1M2M14的节点两两之间的距离变化曲线Fig.15 Distance between arbitrary two nodes of triangle M1M2M14
同理,可测得图11所示机构在收拢过程中其他四面体单元底面三角形的节点两两之间的距离变化曲线,通过计算可得其与初始距离之间的比例系数均为λ0,如图16所示。
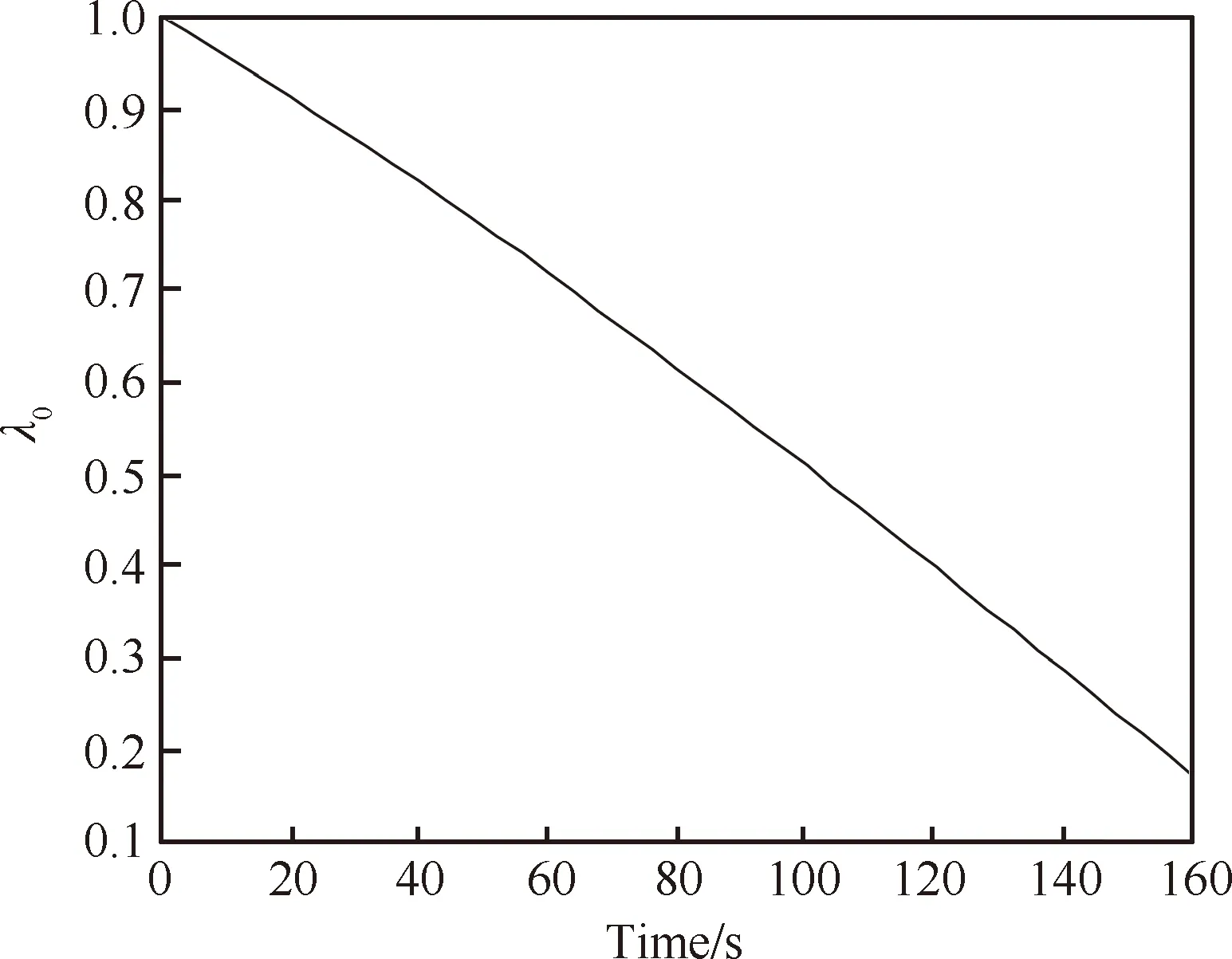
图16 比例收拢系数λ0Fig.16 Value of proportional shrinkage factor λ0
从图12~图14可以看到图11所示的含27个四面体基本可展单元的构架式可展天线机构在避开边界奇异位形后仅在1个驱动作用下实现了收拢运动,且在初始状态位于球面上的所有节点在收拢末态位于同比例缩小的球面上,说明各节点向中心节点A收拢的过程中仅发生了移动运动,姿态未发生改变,此外,图16表明在机构收拢过程中所有四面体基本单元同比例收拢,充分验证了本文基于拆杆等效法对四面体基本可展单元及由其组成的大型构架式可展天线机构的自由度分析的正确性。
4 结 论
1) 基于螺旋理论提出了一种分析空间多环耦合机构自由度的拆杆等效法。将复杂的多环耦合机构拆分为基本并联机构和耦合约束链,基于螺旋理论分析基本并联机构的运动得到等效串联运动链,结合耦合约束链得到多环耦合机构的等效机构,化简了耦合机构的结构,从而通过分析等效机构得到原机构的自由度数目和性质。
2) 应用提出的拆杆等效法将空间多环耦合的四面体单元机构等效为一个单闭环机构,并化简了由其构成的大型构架式可展天线机构的结构,通过分析等效机构得到了四面体基本可展单元及其构成的大型构架式可展天线机构的自由度数目及性质,为进一步分析此类天线机构的运动学和动力学奠定了理论基础。
[1] DAS A, OBAL M W. Revolutionary satellite structural systems technology: a vision for the future[C]//1998 IEEE Aerospace Applications Conference Proceedings. Piscataway, NJ: IEEE Press, 1998: 57-67.
[2] SHIMIZU M. Surface adjustment of modular mesh antenna[C]//Antennas and Propagation Society International Symposium. Piscataway, NJ: IEEE Press, 1994: 2066-2069.
[3] 张润宁, 姜秀鹏. 环境一号C卫星系统总体设计及其在轨验证[J]. 雷达学报, 2014, 3(3): 249-255.
ZHANG R N, JIANG X P. System design and in-orbit verification of the HJ-1-C SAR satellite[J]. Journal of Radars, 2014, 3(3): 249-255 (in Chinese).
[4] JIN M, KAZUHIDE A, YUMI S, et al. Deployment analysis of large space antenna using flexible multibody dynamics[J]. Acta Astronautical, 2000, 47(1): 19-26.
[5] 关富玲, 侯国勇, 赵孟良. 构架式可展开天线结构设计的程序实现[J]. 工程设计学报, 2006, 13(2): 108-113.
GUAN F L, HOU G Y, ZHAO M L. Program implementation of structure design for deployable truss antenna[J]. Chinese Journal of Engineering Design, 2006, 13(2): 108-113 (in Chinese).
[6] 陈务军, 付功义, 董石麟, 等. 扭簧驱动构架式空间展开天线结构分析[J]. 宇航学报, 2001, 22(1):9-13.
CHEN W J, FU G Y, DONG S L, et al. Structural analysis for deployable space truss antenna with rotational springs activated[J]. Journal of Astronautics, 2001, 22(1): 9-13 (in Chinese).
[7] 张京街, 关富玲, 胡其彪, 等. 带弹簧节点的大型构架式展开天线结构的设计和研究[J]. 空间结构, 2000, 6(2):30-37.
ZHANG J J, GUAN F L, HU Q B, et al. Design and study of large deployable truss antenna with spring joints[J]. Spatial Structures, 2000, 6(2): 30-37 (in Chinese).
[8] 张京街, 关富玲, 胡其彪. 大型切割旋转抛物面展开结构的设计[J]. 工程设计学报, 2000, 7(1):46-48.
ZHANG J J, GUAN F L, HU Q B. Design of large cutting-palabolic deployable structure[J]. Chinese Journal of Engineering Design, 2000, 7(1): 46-48 (in Chinese).
[9] XU Y, GUAN F L. Structure-electronic synthesis design of deployable truss antenna[J]. Aerospace Science and Technology, 2013, 26(1): 259-267.
[10] 杨玉龙, 关富玲, 侯国勇, 等. 基于结构解析模型法可展桁架天线结构初步设计[J]. 中国机械工程, 2009, 20(16): 1969-1973.
YANG Y L, GUAN F L, HOU G Y, et al. Deployable tetrahedral truss antenna initial structural design based on interpretative structural model analysis[J]. China Mechanical Engineering, 2009, 20(16): 1969-1973 (in Chinese).
[11] 岳建如, 关富玲, 陈向阳. 大型可展构架式星载抛物面天线结构设计[J]. 浙江大学学报(工学版), 2001, 35(3): 238-243.
YUE J R, GUAN F L, CHEN X Y. A large deployable hexapod paraboloid antenna[J]. Journal of Zhejiang University (Engineering Science), 2001, 35(3): 238-243 (in Chinese).
[12] 黄志荣, 郑士昆, 朱佳龙, 等. 环境一号C星构架反射器展开驱动部件优化设计[J]. 雷达学报, 2014, 3(3): 282-287.
HUANG Z R, ZHENG S K, ZHU J L, et al. Design optimization of expansion driven components for the HJ-1-C satellite[J]. Journal of Radars, 2014, 3(3): 282-287 (in Chinese).
[13] 黄志荣, 宋燕平, 郑士昆, 等. 偏馈式构架反射器构型设计与展开协调性分析[J]. 机械科学与技术, 2016, 35(11): 1791-1796.
HUANG Z R, SONG Y P, ZHENG S K, et al. Analysis of configuration design and deployable coordination of offset-fed truss reflector[J]. Mechanical Science and Technology for Aerospace, 2016, 35(11): 1791-1796 (in Chinese).
[14] 张海波, 李德洪, 高文军, 等. 星载四面体桁架式可展抛物面天线上弦节点定位研究[J]. 空间结构, 2014, 20(3): 61-68.
ZHANG H B, LI D H, GAO W J, et al. Study on upper point location of spaceborne tetrahedron deployable parabolic truss antenna[J]. Spatial Structures, 2014, 20(3):61-68 (in Chinese).
[15] DYER J E, DUDECK M P. Deployable truss structure advanced technology[C]//Proceedings of First NASA/DoD CSI Technology Conference. Washington, D.C.: NASA, 1986: 111-124.
[16] ZIMIN V N, KOLOSKOV I M, MESHKOVSKY V E. Investigation of natural oscillations for self-deployable truss space antennae[J]. Transactions on Modelling and Simulation, 2001, 30: 497-504.
[17] FANG H, SHOOK L, LIN J K H, et al. A large and high radio frequency deployable reflector: AIAA-2012-1838[R]. Reston, VA: AIAA, 2012.
[18] 李波, 杨毅. 星载平面可展天线支撑桁架的结构效率优化[J]. 航空学报, 2015, 36(12): 3853-3860.
LI B, YANG Y. Optimization for structure efficiency of a deployable spaceborne truss with flat panel antennas[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(12): 3853-3860 (in Chinese).
[19] 黄真, 刘婧芳, 李艳文. 150年机构自由度的通用公式问题[J]. 燕山大学学报, 2011, 35(1): 1-14.
HUANG Z, LIU J F, LI Y W. 150-year unified mobility formula issue[J]. Journal of Yanshan University, 2011, 35(1): 1-14 (in Chinese).
[20] BAGCI C. Degrees of freedom of motion in mechanisms[J]. Journal of Engineering for Industry, 1971, 93(1): 140-148.
[21] LI Y W, WANG L M, LIU J F, et al. Applicability and generality of the modified Grubler-Kutzbach criterion[J]. Chinese Journal of Mechanical Engineering, 2013, 26(2): 257-263.
[22] DAI J S, HUANG Z, LIPKIN H. Mobility of overconstrained parallel mechanisms[J]. Journal of Mechanical Design, 2006, 128(1): 220-229.
[23] 杨廷力, 沈惠平, 刘安心, 等. 机构自由度公式的基本形式、自由度分析及其物理内涵[J]. 机械工程学报, 2015, 51(13): 69-80.
YANG T L, SHEN H P, LIU A X, et al. Review of the formulas for degrees of freedom in the past ten years[J]. Journal of Mechanical Engineering, 2015, 51(13): 69-80 (in Chinese).
[24] ZHANG Y T, LU W J, MU D J, et al. A novel mobility formula for parallel mechanisms expressed with mobility of general link-group[J]. Chinese Journal of Mechanical Engineering, 2013, 26(6): 1082-1090.
[25] 刘婧芳, 黄晓鸥, 余跃庆, 等. 多环耦合机构末端件自由度计算的等效法[J]. 机械工程学报, 2014, 50(23): 89-96.
LIU J F, HUANG X O, YU Y Q, et al. Equivalent method of output mobility calculation for a novel multi-loop coupled mechanism[J]. Journal of Mechanical Engineering, 2014, 50(23): 89-96 (in Chinese).
[26] 高慧芳, 刘婧芳, 黄晓欧. 基于独立运动分流标记法的多环耦合机构自由度分析方法[J]. 北京工业大学学报, 2015, 41(11): 1658-1664.
GAO H F, LIU J F, HUANG X O. Method of mobility calculation for a coupled mechanism based on independent motion shunting measurement[J]. Journal of Beijing University of Technology, 2015, 41(11): 1658-1664 (in Chinese).
[27] 沈惠平, 邵国为, 朱小蓉, 等. 基于POC法的多环耦合并联机构拓扑特征分析[J]. 农业机械学报, 2016, 47(4): 349-354.
SHEN H P, SHAO G W, ZHU X R, et al. POC method based topology characteristic analysis of multi-loop coupled mechanisms[J]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(4): 349-354 (in Chinese).
(责任编辑: 李世秋)
*Corresponding author. E-mail: yszhao@ysu.edu.cn
Mobility analysis of a deployable truss-antenna mechanism—Method based on link-demolishing and equivalent idea
XU Yundou1,2, LIU Wenlan1, CHEN Liangliang1, YAO Jiantao1,2, ZHAO Yongsheng1,2,*, ZHU Jialong3
1.ParallelRobotandMechatronicSystemLaboratoryofHebeiProvince,YanshanUniversity,Qinhuangdao066004,China2.KeyLaboratoryofAdvancedForging&StampingTechnologyandScienceofMinistryofNationalEducation,YanshanUniversity,Qinhuangdao066004,China3.ChinaAcademyofSpaceTechnology(Xi’an),Xi’an710100,China
A method for Degree Of Freedom (DOF) analysis of spatial mechanisms with multiple coupled-loops is proposed based on the link-demolishing and equivalent idea, in view of the multi-loop coupling characteristic of a deployable truss antenna assembled by tetrahedral elements. The coupling constraint chain of the deployable tetrahedral element is removed, and the remainder is regarded as a parallel mechanism. The number and characteristic of the DOF of each output node are then analyzed using the screw theory, and the equivalent serial kinematic chain between the output nodes and the fixed node are then established. The equivalent mechanism of the deployable tetrahedral element is obtained by reconstructing the coupling constrained chain. The number and characteristic of the DOF of the equivalent mechanism are got using the modified G-K formula and the reciprocal screw theory, respectively. As a result, the kinematic characteristics of the tetrahedral element are known. The structure of the minimum composite unit and the large-scale truss deployable antenna are simplified, according to the equivalent mechanism and the combination of the tetrahedral elements. The numbers of the DOF of the minimum composite unit and the large-scale truss deployable antenna are derived on the basis of the geometric constraint equations. The simulation model for a deployable truss antenna assembled by 27 tetrahedral elements is built, and its DOF is verified. The result shows that the DOF of the antenna analyzed by the proposed method is correct. The method lays a foundation for further analysis of the kinematics and dynamics of similar type of antennas, providing a new idea for DOF analysis of other multi-loop coupling mechanisms.
link-demolishing and equivalent method; tetrahedron cell; deployable antennas; mobility; screw theory
2017-02-24; Revised: 2017-03-13; Accepted: 2017-03-21; Published online: 2017-04-19 11:24
URL: www.cnki.net/kcms/detail/11.1929.V.20170419.1124.006.html
s: National Natural Science Foundation of China (51675458); Key Project of Natural Science Foundation of Hebei Province (E2017203335); Youth Top Talent Project of Hebei Province Higher Education (BJ2017060)
V243.4; TH112
A
1000-6893(2017)09-421188-12
2017-02-24; 退修日期: 2017-03-13; 录用日期: 2017-03-21; 网络出版时间: 2017-04-19 11:24
www.cnki.net/kcms/detail/11.1929.V.20170419.1124.006.html
国家自然科学基金(51675458); 河北省自然科学基金重点项目(E2017203335); 河北省高等学校青年拔尖人才计划项目 (BJ2017060)
*通讯作者.E-mail: yszhao@ysu.edu.cn
许允斗, 刘文兰, 陈亮亮, 等. 构架式可展天线机构自由度分析——拆杆等效法[J]. 航空学报, 2017, 38(9): 421188. XU Y D, LIU W L, CHEN L L, et al. Mobility analysis of a deployable truss-antenna mechanism—Method based on link-demolishing and equivalent idea[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(9): 421188.
http://hkxb.buaa.edu.cn hkxb@buaa.edu.cn
10.7527/S1000-6893.2017.421188
——三角形一个共线点命题的空间移植

