小波在BPSK通信对抗干扰效果评估中的应用

樊占军，王 宁

(解放军91336部队，河北 秦皇岛 066000)

小波在BPSK通信对抗干扰效果评估中的应用

樊占军，王 宁

(解放军91336部队，河北 秦皇岛 066000)

随着信息通信技术的快速发展，通信对抗技术也迎来了飞速发展的时期，通信信号调制类型的识别越来越受到重视，而由于小波具备较好的时-频局部化效果，导致基于小波理论的信号识别应用越发广泛。从二进制相移键控(BPSK)调制的特性和小波的时频特性展开，选取了Daubechies小波进行调制，确定待评估信号与原信号的距离Dv为特征值，采用System View系统进行仿真实验，并得出了一定的结论。

通信对抗；二进制相移键控调制；小波理论；Daubechies小波

0 引 言

在日新月异的现代通信与通信对抗技术领域，通信信号调制作为通信与通信对抗技术的必要手段受到了业内人士的重视，而小波因其能够提供一个信号局部化的频域信息，导致基于小波理论的通信信号识别与通信对抗干扰效果评估也受到了关注。

1 小波和小波变换

小波这一专业术语，从字面上理解，指的是比较小的波形变化，“小”表示这种波形具有独特的衰减性，而“波”则是说明其具有波动共性。“小波变换”的概念是由法国的J Morelet工程师提出的，是对时间、空间、频率进行局部分析的一种方法，也可以称之为“窗口化”分析，因为其可以进行伸缩平移，这样就可以对信号进行多尺度细化分析，实现对信号低频的频率细分与高频的时间细分，对时频信号的分析可以自行适应，以达到对信号任意细节的细化分析，直接让先前Fourier变换无法解决的许多问题迎刃而解，是信号调制分析技术发展史上的一个重大突破[1-3]。

2 信号调制样式的选取

信号调制指的是利用一个信号去控制另外一个信号，按照其要求的“固有参数”进行变换。一般情况下称控制信号为调制信号，而被控制的信号称之为载波信号，载波信号一般选取正弦信号。而所谓的“固有参数”则是指幅值、频率、相位和脉冲宽度等参数。一般情况下，数字信号按照幅值、频率和相位进行调制的基本方法可以简化写成幅移键控(ASK)、频移键控(FSK)、相移键控(PSK)，而由于PSK具有较强的抗噪性和较小的误码率，使得其能够在信号环境更加复杂的军用通信领域得到认可与应用[4]。

在传输对象通常是二元数字信息的数字调制通信中，二进制相移键控(BPSK)是采用二进制基带信号(0或1)对正弦载波进行调制，也可以称之为2PSK调制，因此BPSK已调信号可表示为：

SBPSK(t)=[∑ang(t-nTs)]cosωct

(1)

若g(t)是宽度W=Ts的单位矩形脉冲，则SBPSK(t)可以表示为：SBPSK(t)=±cosωct=cos(ωct+φi)，φi=0，π其信号波形如图1所示。

图1 BPSK调制信号

从图1可见，当横轴上信息x=1时(从0到1的过程)，SBPSK(t)的相位发生了相反方向的变化，相位ωct+φi=2πft+φi，所以频率f也一定发生了变化。

对于BPSK信号而言，已调信号相位与未调载波的相位相同时，表示二进制数字信号0；与未调载波的相位相反时，表示二进制数字信号1。因此BPSK是以一个固定初相的未调载波为参考，所以接收BPSK信号只能采用相干解调方法。

BPSK信号可以表示为：

(2)

对于BPSK信号的干扰一般采用单频正弦干扰，可以表示为:

Uj(t)=Ujcos(ωjt+φj)

(3)

为了研究方便，一般设ωj=ωs，即干扰信号与通信信号之间的频率相重合，仅存在相位上的差异。

当BPSK信号以等概率发送0、1码时，总的错误概率可以表示为：

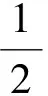
(4)

上式表明，BPSK信号的错误接受率很低，它的抗干扰性比较强，频带利用率较高，是一个性能较好的数字调制信号。

3 基于小波的BPSK通信对抗干扰效果评估办法

3.1 选取合适的小波

因为小波可以进行伸缩平移，实现了对信号的多尺度细化分析，即对信号低频的频率细分与高频的时间细分，这正符合高频信号迅速变换、低频信号缓慢变换的信号特点。而从图1也可以看出，BPSK信号调制方式也具备同样的特点。所以利用小波的变化特性可以对BPSK信号进行更为有效的处理，还因为小波变换具有时频灵活性，使得通信信号的处理能达到频域到时域的平滑变换。所以，当使用合适的小波去识别BPSK信号时，可以达到实时的效果[5]。

假设一个信号s(t,γ(t))，其参数γ(t)变化时发生瞬时响应。一个典型的母小波如果要很好地探测到信号的瞬时变化，必须满足以下条件：

(1) 如果没有瞬时变化，小波变换应保持稳定的输出，即γ(t)不发生变化时，有S(t,γ(t))=k，其中对于给定的α，k为与τ相关独立的常数。

(2) 如果一个瞬时变化的发生使得γ(t)在时间t=T内发生变化，那么在瞬时变化的点位，小波变换的输出相对于常数k将有一个明显的变化。

(3) 在时刻T内，小波变换的输出与常数k出现最大的不同点。

为了满足以上条件，当信号γ(t)保持不变时，其小波变换也一定不变，而当信号γ(t)发生变化时，小波变换一定会出现一个峰值。另外还要求小波具有明显的探测性能，小波的选取是影响干扰效果评估特征值选取的一个比较重要的因素。为此，需要选取局部特性较好的小波，正交小波一般会满足上述条件。选取时，考虑具有正交特性的Daubechies小波，由于Daubechies小波是正交小波，这种紧支集小波的局部特性好，且具有良好的逼近性与确定性，能够构造具有有限支集的正交小波，因此最终选用了具有正交特性的Daubechies小波。

3.2 特征值的选取

对于如何提取调制信号的信号特征，一般使用小波变换的方式。提取信号特征的方法分为2种：一是采用在小波连续变换时，利用起模极大值提取信号的特征；二是对调制信号进行多分辨率分析，以达到多层小波分解的效果，来提取信号特征。

假设存在这样一个通信信号序列，其长度是有限的，那么可以表示为：

s0={s0,n|n=1-N,2-N,…,0,1,…,L-1,

L,…,L+N-1}

(5)

小波的低通滤波器系数为{h0,h1,…,hN}，N由{h0,h1,…,hN}所确定；L为任意正整数。

根据Mallat算法，S0的小波分解为:

(6)

小波系数为：

(7)

数字信号的已调信号一般均为带限信号，信号调制类型不同，在同一水平下其相关信号的细节也存在较大差别，同时，与其他的数字调制信号相比，BPSK信号中频率信息包含得更加丰富，应用小波分解可以得到BPSK信号在不同频率下的离散逼近和离散细节，从而得到较好的干扰效果评估特征值。

当在BPSK信号中加入噪声时，其小波分解细节在同一分解水平下存在很大差别，在信号相位受到干扰时，其小波变换的能量的变化也不尽相同，造成对信号的破坏程度也随噪声能力的改变而改变，因此选择干扰效果评估的特征向量为:

(8)

式中:dm,n表示分解水平下的离散细节，m=1,2,…,M，M为选取信号的小波分解水平，n为信号点数。

在干扰效果评估应用中，一般应用距离函数作为干扰效果评估的特征值，由此在小波理论的基础上定义的距离函数如下：

Dv(d,dBPSK)=∑(t-tBPSK)2=∑(d-dBPSK)2

(9)

式中：d表示加噪信号的小波变换的离散细节；dBPSK表示原信号小波变换的离散细节。

根据定义，Dv表示待评估信号与原信号的距离。评估时将距离按评估指标分为几个等级，根据距离的大小程度可以判断干扰效果的等级。因此将Dv设置为干扰效果评估的特征值。

3.3 BPSK干扰效果评估方法

当BPSK信号的2个相邻码元出现相位跳变时，获得的由特征向量产生的脊线会在相位跳变点附近产生明显的尖峰。但当信号加入噪声之后，所提取的脊线会根据噪声的大小出现不同的波动。因此加入噪声后的脊线模值与原信号的脊线模值相比会有所变化，因此距离函数Dv可以体现干扰效果的等级。其步骤为：

(1) 利用3.2所示小波变换的方法获得所需要的小波系数dm+1,n，进而计算得到干扰效果评估特征值；

(2) 设置一个合理的阈值T，当Dv与T的差大于某值时，可以说其干扰有效。

对于信号SBPSK(t)=cos(ωct+φi)，当φi=0°时，相位不变；当φi=180°时，相位跳变。而频率也会随着相位跳变而进行变化，因此对BPSK信号可以进行一个尺度层次的小波分解。

根据上述分析结果，此时应选择具有正交特性的Daubechies小波。由于在信号相位发生变化时，其变化频率相对于码速率来说比较高，相位的跳变将反映在小波系数的高频段，因此要取小波变换的高频部分。小波高频系数的特征向量值将在一个小的直流层上进行显著的变化，就像一个个脉冲。

当信号中存在噪声时，如果噪声增大，那么其信号脉冲也会产生明显的变化，因此经过实验可以得出结论：无论是加高斯白噪声还是加有色噪声，也无论原信号的强度大小，噪声的增加都极大地提高了特征值的变化。噪声越大，BPSK信号识别越难，就不能辨别模值的脉冲形成。因此，利用特征值t求出的干扰效果评估特征值Dv可以较好地反映信号被干扰的效果，当Dv超过预定的阈值时可以判定干扰有效。

3.4 BPSK干扰效果仿真实验结果

通信对抗干扰效果评估试验中，对于数据通信，一般都是利用误码仪测量通信系统的误码率，根据误码率的实际大小来确定干扰效果的等级。当通信接收方的数据误码率达到一定程度时，在战场上接收的数据将无法理解，为无效的通信数据，此时可认为其干扰效果有效。

仿真实验是基于System View系统进行的，为了获得与常用评估方法相一致的结论，实验时采用距离函数Dv的评估结果与数据的误码率评估结果进行比对。

(1) 在基于System View系统所建的仿真系统里，设置一个信号模式为二元数字信号的BPSK数字调制通信系统，通过系统仿真后得到原始的没有经过解调的BPSK通信信号和解调过的通信信号。此时系统中没有干扰信号，计算其特征值，未解调的信号用于计算信号的Dv值，而解调过的通信信号用于计算数据通信的误码率。

(2) 在(1)的基础上给通信信号系统加入高斯白噪声信号，用同样的方式得到有噪声的未解调信号和经过解调的信号。然后，再通过不断调整的大小来获得对应噪声环境下的未解调的信号，进而计算出其对应的特征值与相应的误码率。

(3) 为获取不同情况下的评估结果，以证实评估方法的可靠性，设置不同的数据类型、数据速率、载频速率、采样时间和噪声，重复步骤(1)、(2)，得出实验结果，选2种典型的结果，如图2和图3所示。

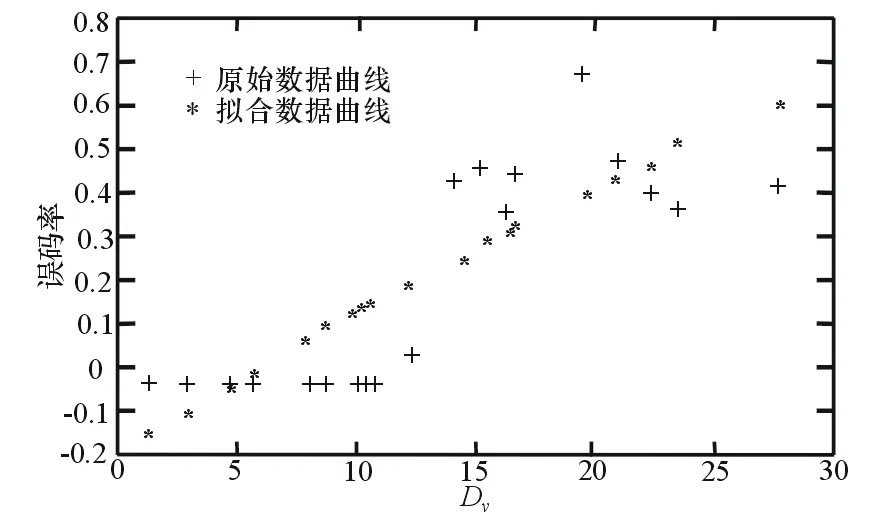
图2 信息10011001001…加高斯白噪声的Dv与误码率的关系

图3 随机信息加有色高斯白噪声的Dv与误码率的关系

由图2和3可知，当干扰信号的强度增加到一定程度，BPSK信号的Dv值达到预定的阈值后，信号的误码率也会到一定的量值，这个量值即为干扰有效时的参考值，此时可定义为干扰效果有效。因此从结果上可以看出，由Dv值进行的干扰效果评估结果与常用的以误码率为标准的干扰效果评估结果可以达到一致。经过长期试验的积累，可以得到不同通信系统的Dv值，用以评估不同条件下的干扰效果。

4 结束语

通过以上仿真结果可以看出，计算距离函数Dv可以体现干扰效果的等级。这种通信对抗干扰效果评估方法可以一定程度上降低仿真过程中因解调而带来的评估误差，更有利于仿真试验中的干扰评估。

[1] 郭黎利.通信对抗应用技[M].哈尔滨:哈尔滨工程大学出版社，2007.

[2] BURRUS C S.小波与小波变换导论[M].程正兴译.北京：电子工业出版社，2013.

[3] 李炎新，胡爱群，宋宇波.自适应BPSK解调方法研究[J].中国工程科学，2006,8(5):49-51.

[4] 陈祥训.对几个小波基本概念的理解[J].电力系统自动化，2004，28(1):1-6.

[5] 王继祥，韩慧.通信对抗干扰效果可观评估[M].北京：国防工业出版社，2012.

ApplicationofWavelettoTheJammingEffectEvaluationofBPSKCommunicationCountermeasure

FAN Zhan-jun,WANG Ning

(Unit 91336 of PLA,Qinhuangdao 066000,China)

With the fast development of information communication technology,the communication countermeasure technology has come to a full-speed developing period.The identification of communication signal modulation type has been paid for more and more attention.The signal identification based on wavelet theory has been applied widely because of its better localization effect in time-frequency domain.This paper starts with the modulation characteristic of binary phase shift keying (BPSK) and time-frequency characteristic of wavelet,and chooses the Daubechies wavelet to make modulation,confirms the distanceDvbetween the signal assessed and original signal as characteristic value,adopts the System View to perform simulation experiment,and fetches definite conclusion.

communication countermeasure;binary phase shift keying modulation;wavelet theory;Daubechies wavelet

TN975

A

CN32-1413(2017)05-0052-04

10.16426/j.cnki.jcdzdk.2017.05.011

2017-03-25