舰载雷达侦察系统坐标系转换方法

闫秋飞，王 聪

(中国船舶重工集团公司第七二三研究所，江苏 扬州225001)

舰载雷达侦察系统坐标系转换方法

闫秋飞，王 聪

(中国船舶重工集团公司第七二三研究所，江苏 扬州225001)

介绍了舰载雷达侦察系统常用坐标系转换方法，包括舰船地理坐标系到舰船甲板坐标系的变换及逆变换、舰船甲板坐标系到阵面坐标系的变换及逆变换，给出了具体的推导过程及坐标系相互转换的公式，结合坐标系转换的理论方法，阐述了舰载雷达侦察系统坐标系转换的应用实例。

坐标变换；舰船地理坐标系；舰船甲板坐标系；阵面坐标系；纵摇角；横摇角

0 引 言

舰船在水面航行时，航向、纵摇、横摇会发生改变，为保证雷达侦察系统测向的稳定，使目标指向在惯性空间内稳定，一般采用坐标变换技术对舰船的摇摆姿态角进行角度的实时补偿。在舰载雷达侦察系统中，利用平台罗经测得的舰船航向角、纵摇角、横摇角实时送给雷达侦察系统，雷达侦察系统根据在船上的安装位置实时进行角度补偿，得到目标的稳定坐标系[1]。

1 坐标系模型

1.1 地球模型

在仿真中，涉及到大量的空间位置关系及目标姿态等的计算，这些都是在一定的参考坐标系中进行的，而这些都是以地球为惯性参考系的，地球模型是保持空间一致性的基础。选择合适的坐标系，对于保证空间的一致性、简化计算是非常重要的。

地球可以近似看作是一个椭球，公式为：

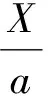
(1)

式中：X，Y，Z为地球表面上的一点；a为地球长半轴长度，约为6 378 137 m;b为地球短半轴长度，约为6 356 752 m，于是有:

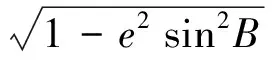
(2)

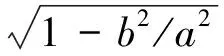
(3)

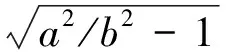
(4)

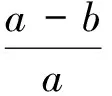
(5)

η=e′cosB

(6)

(7)

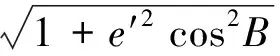
(8)

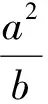
(9)

(10)

式中:RN为P点的卯酉圈曲率半径，单位为m;e为地球第一偏心率常数;e′为地球第二偏心率常数;f为椭球的扁率[2]。

1.2 大地坐标系

空间一点P的大地坐标用大地纬度B、大地经度L和大地高度H表示。其中，P点的大地子午面和起始大地子午面所构成的二面角L是P点的大地经度，从起始大地子午面算起，向东为正，向西为负；P点的法线和赤道面的夹角B是P点的大地纬度，从赤道面算起，向北为正，向南为负；P点沿法线到地球球面的距离H是大地高，从地球球面起，向外为正，向内为负，图1为地球参考模型[3]。

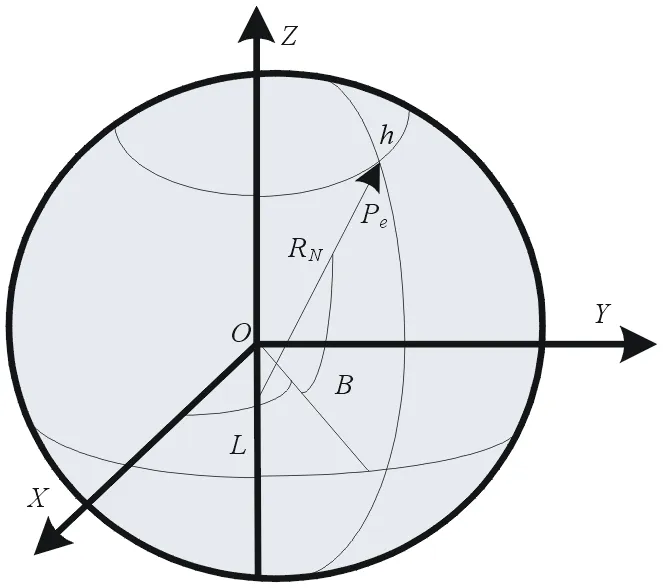
图1 地球参考模型

1.3 舰船地理坐标系

如图2所示，舰船地理坐标系OXYZ原点O位于船体摇摆中心；OX轴平行于水平面指向正东；OY轴指向水平面指向正北；OZ轴垂直于OXY平面，向上为正[4]。

图2 舰船球面坐标及摇摆角模型

1.4 舰船甲板坐标系

如图2所示，舰船甲板坐标系OXbYbZb原点O位于船体摇摆中心；OYb平行于艏艉线指向舰艏；OXb轴与OYb垂直且平行于甲板平面，指向右舷；OZb垂直于OXbYb平面，向上为正。

1.5 阵面坐标

如图3所示，阵面坐标系OXcYcZc原点O位于阵面中心；OYc为阵面法线；OXc在阵面平面内垂直于OYc，向右为正；OZc垂直于面OXcYc，向上为正。

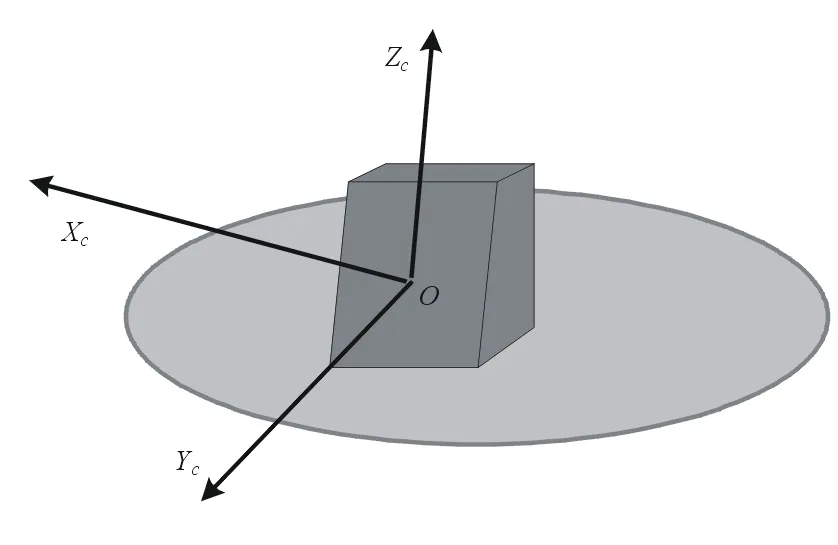
图3 阵面坐标模型

1.6 航向及姿态角定义

如图2所示，航向角H为从正北开始顺时针到舰艏方向的夹角，在水平面内测量，顺时针为正，ON与OD的夹角为航向角。纵摇、横摇定义如图2所示，BCDEFNG为水平面，MHJKL为甲板平面，纵轴JL为舰船艏艉线，O为舰船摇摆中心，A为天顶。横轴OH指向右舷为Xb轴，纵轴OJ指向舰艏为Yb轴，OS垂直于OXbYb面为Zb轴，OH、OJ、OS构成OXbYbZb舰船甲板坐标系。舰船的大地直角坐标位于水平面内，OE指向正东X轴，ON指向正北为Y轴，OA指向天顶为Z轴，OE、ON和OA构成OXYZ的舰船地理坐标系。甲板平面的纵摇角P为舰船艏艉线与水平面的夹角，在垂直平面内测量，弧DJ为纵摇角，向上方为正。甲板平面横摇角R为甲板平面绕舰船艏艉线旋转的角度，即舰船横剖面水平面的交线与舰船横轴之间的夹角，弧HC为横摇角，右舷下为正[5]。

2 坐标系之间的转换

2.1 舰船地理坐标系与舰船甲板坐标系之间的转换

舰船地理坐标系到甲板坐标系的变换需按航向变换、纵摇变换及横摇变换的顺序进行。

如图4所示，航向变换OXYZ坐标系绕OZ轴旋转H后的坐标系为OXHYHZ，B点在OXYZ坐标系中的坐标为(x,y,z)，在OXHYHZ坐标系中的坐标为(xH,yH,z)，B点在水平面内的投影为B′，r=OB′，r与Y轴夹角为方位A，OB与OB′的夹角为俯仰E，由图4可知：

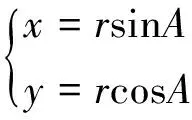
(11)

xH=rsin(A-H)=

rsinAcosH-rcosAsinH=

xcosH-ysinH

(12)

yH=rcos(A-H)=

rcosAcosH+rsinAsinH=

xsinH+ycosH

(13)

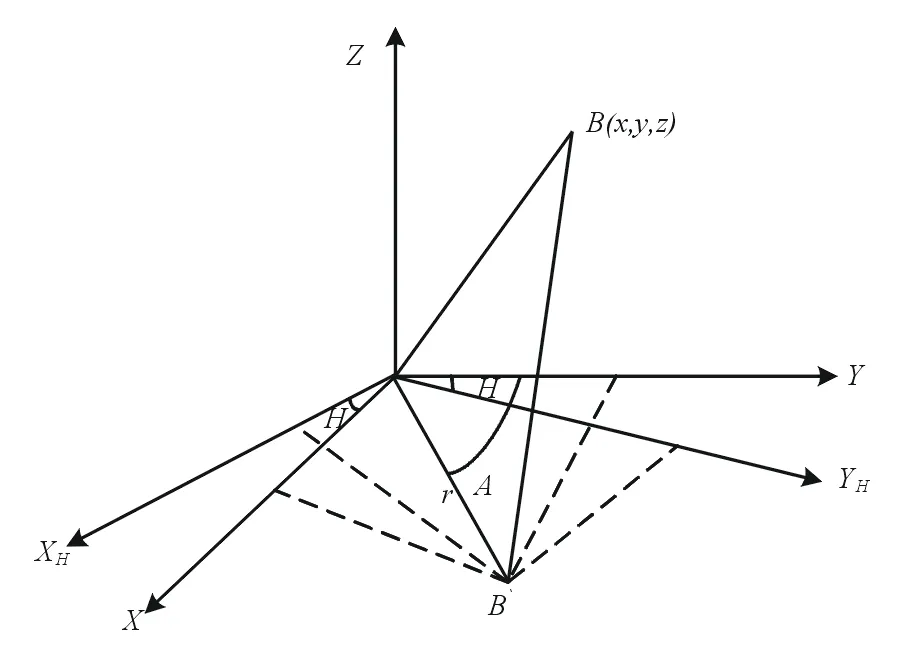
图4 按航向变换模型图

则航向角变换矩阵为：

(14)

其逆矩阵为：

(15)

如图5所示，纵摇变换OXYZ坐标系绕OX轴旋转P后的坐标系为OXYPZP，B点在OXYZ坐标系中的坐标为(x,y,z)，在OXYPZP坐标系中的坐标为(x,yP,zP)，B点在铅锤面内的投影为B′，r=OB′，r与Y轴夹角为F，由图5可知：

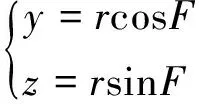
(16)

yP=rcos(F-P)=

rcosFcosP+rsinFsinP=

ycosP+zsinP

(17)

zP=rsin(F-P)=

rsinFcosP-rcosFsinP=

zcosP-ysinP

(18)

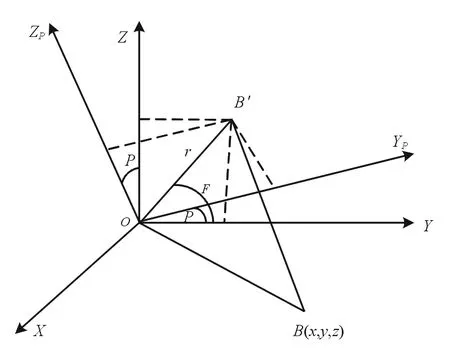
图5 按纵摇变换模型图

则纵摇角变换矩阵为：

(19)

逆矩阵为：

(20)

如图6所示，横摇变换OXYZ坐标系绕OY轴旋转R后的坐标系为OXRYZR，B点在OXYZ坐标系中的坐标为(x,y,z)，在OXRYZR坐标系中的坐标为(xR,y,zR)，B点在XOZ面内的投影为B′，r=OB′，r与Z轴夹角为R，由图6可知：

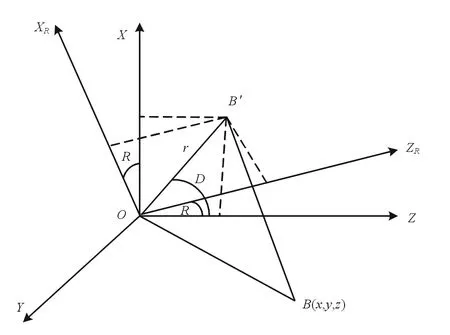
图6 按横摇变换模型图

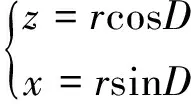
(21)

zR=rcos(D-R)=

rcosDcosR+rsinDsinR=

zcosR+xsinR

(22)

xR=rsin(D-R)=

rsinDsinR-rcosDsinR=

xcosR-zsinR

(23)

则横摇角变换矩阵为：

(24)

逆矩阵为：

(25)

由以上推导可知舰船大地坐标系到甲板坐标系之间的变换矩阵为：

mb=mR·mP·mH

(26)

坐标变换为：

(27)

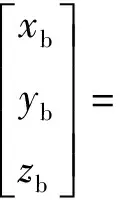
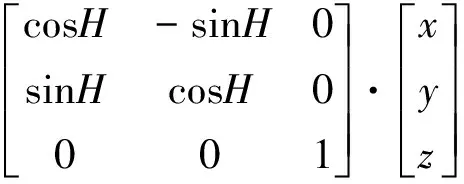
(28)

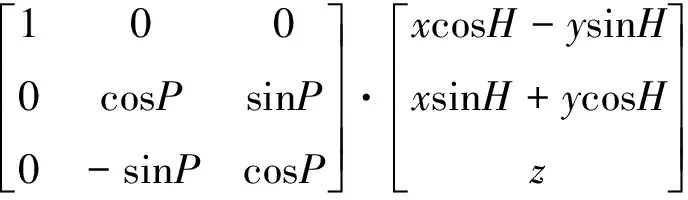
(29)

(30)

(31)

2.2 舰船甲板坐标到阵面坐标的转变

雷达侦察系统阵面安装时，由于安装在甲板的不同位置，相对于舰艏艉线阵面有一定的方位安装偏角和俯仰安装倾角，假设阵面相对于舰艏艉线的方位安装偏角为HH，俯仰安装偏角为EE，根据图3，由甲板坐标到阵面坐标的转换首先沿Z轴旋转，然后沿X轴旋转[6]。绕Z轴旋转的旋转矩阵为：

(32)

逆矩阵为：

(33)

绕X轴旋转的旋转矩阵为：

(34)

逆矩阵为：

(35)

由舰船甲板坐标到阵面坐标的旋转矩阵为：

mc=mPP·mHH

(36)

坐标变换为：

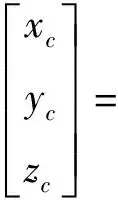
(37)

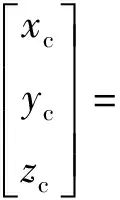
(38)

(39)

3 坐标系变换在电子对抗系统中的应用

3.1 姿态信息使用流程

如图7所示，舰船上的姿态仪把航向、纵摇、横摇等姿态信息送上级系统，上级系统把姿态信息送雷达侦察系统设备主控，设备主控把姿态信息转发给后端接收处理，接收处理把姿态信息转发给不同象限的阵面。其中航向角为艏艉线与真北方向的夹角，顺时针为正，取值范围0～360°;纵摇角规定艏高为正，艏低为负;横摇角规定左舷高为正，左舷低为负。

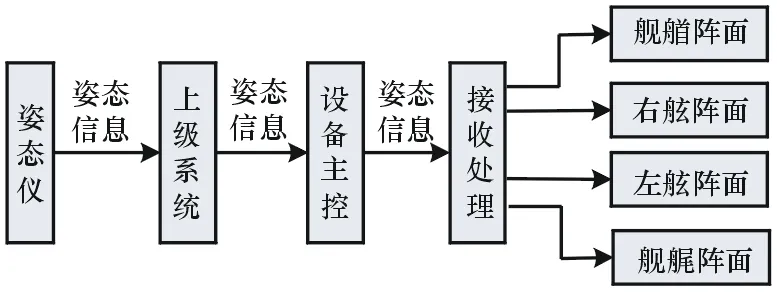
图7 舰船姿态信息使用流程

3.2 阵面坐标到舰船甲板坐标变换

在舰载雷达侦察系统的应用中，首先把阵面坐标系下测得的方位Ac、俯仰Ec转换为甲板坐标系下的方位和俯仰。

假设目标在阵面直角坐标系下的坐标为：

(40)

转换为舰船甲板坐标系下的坐标，转换矩阵:

(41)

坐标转化为：

(42)

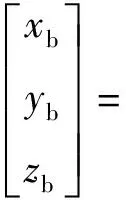
(43)

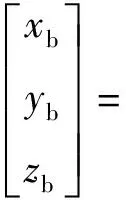
(44)

(45)

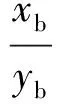
(46)

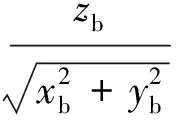
(47)

式中：Ab和Eb分别为目标在舰船甲板坐标系下的方位和俯仰。

3.3 舰船甲板坐标到舰船大地坐标变换

由舰船甲板坐标系下的坐标转换为大地直角坐标系下的坐标(x,y,z)，转换矩阵为：

(48)

(49)

坐标变换如下：

(50)

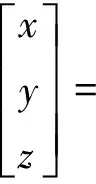
(51)

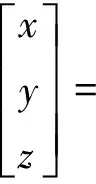
(52)

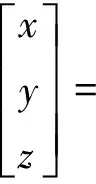
(53)

(54)

(55)

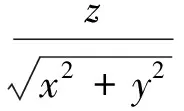
(56)

式中：A和E分别为目标在舰船甲板坐标系下的方位和俯仰。

4 结束语

针对舰载雷达侦察系统常用的舰船大地坐标、舰船甲板坐标、阵面坐标，本文给出了相互转化方法并对公式进行了推导，对舰载雷达侦察系统的坐标变换实际应用进行了说明，对舰载雷达及侦察系统的坐标变换具有一定的指导意义。

[1] 曹正才.舰载雷达常用稳定方式坐标变换[J].雷达与对抗，2010,30(1):48-52.

[2] 胡明城.全球定位系统(GPS)的最新进展[J].测绘科学，2001(1)：38-43.

[3] 张勤，要家权.GPS测量原理及应用[M].北京.科学出版社，1996.

[4] 张志远，罗国富.舰船姿态坐标变换及稳定补偿分析[J].舰船科学技术，2009,31(4)：34-40.

[5] 王有朝.对舰艇纵横摇坐标变换的讨论[J].现代雷达，2001(4)：27-30.

[6] 王航宇，王士杰，李鹏.舰载火控原理[M].北京：国防工业出版社，2006.

CoordinateTransformationMethodsofShipboardRadarReconnaissanceSystem

YAN Qiu-fei,WANG Cong

(The 723 Institute of CSIC,Yangzhou 225001,China)

This paper introduces the common coordinate transformation methods of shipboard radar reconnaissance system,such as the transformation and inverse transformation of ship geographic coordinate to ship deck coordinate,the transformation and inverse transformation of ship deck coordinate to array coordinate,presents the specific derivation process and coordinate transformation formulas,expatiates the application example for coordinate transformation of shipboard radar reconnaissance system combined with the theoretical method of coordinate transformation.

coordinate transformation;ship geographic coordinate;ship deck coordinate;array coordinate;pitching angle;rolling angle

TN957.51

A

CN32-1413(2017)05-0034-06

10.16426/j.cnki.jcdzdk.2017.05.007

2017-06-29