国债供求与动态利率期限结构
——基于DRA模型的实证分析
(山东财经大学金融学院,山东 济南 250014)
引言与文献综述
国债利率期限结构在货币政策传导、预测宏观经济变量未来趋势等方面发挥重要作用,因而利率期限结构变化的影响因素以及与宏观经济变量之间的关系是金融学研究的热点之一。在这一问题的研究过程中,越来越多的学者注意到国债供求变化通过利率期限结构的传导对宏观经济变量产生的可能影响。例如,Gagnon.etc(2010,2011)[10]、D’Amico and King(2011)[6]、Krishnamurthy and Vissing-Jorgensen(2011)[15]、Hamilton and Wu(2012)[12]等利用事件研究法及线性回归模型测算了美国实施“大规模资产购买”及“扭曲操作”等非常规货币政策时,直接增加中长期国债需求对利率期限结构的影响;而Meaning and Zhu(2012)[16]则测算政府债务管理者增加长期债券供给对央行扭曲操作政策的抵消效应。Canlin Li and Min Wei(2013)[2]及Kaminska and Zinna(2014)[14]在Vayanos和Vila(2009)[18]、Greenwood和Vayanos(2013)[11]提出的(修正后的)优先偏好(preferred habitat)利率期限结构模型基础上,分别构建了含有供给因素和需求因素的无套利利率期限结构模型,并以美国国债数据进行实证检验。
随着利率市场化进程的推进及国债市场规模的扩大,国债市场及利率期限结构在我国货币政策及宏观经济调控中的地位越来越重要。相关研究的主要方法可分为两大类:一是先针对利率期限结构数据,利用主成份分析或者Nelson-Siegel动态模型,得到所谓的“水平”、“斜率”和“曲度”等状态因子的时间序列;然后再将这些序列与CPI,货币量,GDP等宏观变量的时间序列建立VAR模型或多元线性回归模型。例如,潘敏和夏庆(2012)[19]、丁志国(2014)[20]、张旭等(2016)[21]等。张雪莹(2014)[22]、陈浪南和郑衡量(2015)[23]采用这种类似的“两步法”,引入了国债流通总额、长期国债占比等债券供给变量,连同银行存贷差、通货膨胀率、工业增加值等债券需求及宏观变量一起,检验对利率期限结构的影响;但显然在这类方法中,利率期限结构因子的求解与与宏观因素、国债供求等变量实际上是分离的。第二类研究路线是直接将利率期限结构模型与宏观经济模型联合建模,其中,利率期限结构模型可以用Diebold、Rudebusch和Aruoba(2006)[8]提出的动态Nelson-Siegel模型(也称为DRA模型)加以描述,如吴吉林等(2010)[24]、沈根祥(2011)[25]、王雪标和龚莎(2013)[26]、尚玉皇等(2015)[27]、沈根祥和陈映洲(2015)[28]等;也可以采用仿射利率期限结构形式,在无套利条件约束下构建所谓的宏观-金融模型(macro-finance),例如,孙皓和石柱鲜(2011)[29]、袁靖和薛伟(2012)[30]、曾耿明和牛霖琳(2013)[31]、耿迎涛和丁志国(2015)[32]、金成晓和李雨真(2015)[33]等。遵循这一研究路线,只有极少数研究考虑了国债市场中供求力量的变化,例如Fan, Li and Zhou(2013)[9]以官方贷款利率及银行存贷差反映债券需求因素,考察其对部分关键期限利率的影响,但模型没有考虑债券供给因素以及其它宏观变量的影响。韩国文(2016)[34]在Vayanos和Vila(2009)[18]提出的两因子利率期限结构模型的基础上引入了政府供给因素,从而构建了国债供给影响利率期限结构的理论模型。但是,其实证部分也是直接利用多个关键期限利率数据来衡量利率期限结构,忽略了因子结构能够充分描述债券收益率的期限结构这一事实;而且文章只是采用简单的OLS回归进行分析,不能得出更加丰富直观的结论。
本文在Diebold, Rudebusch和Aruoba(2006)[8]提出的DRA模型基础上引入国债供求变量,分析国债供求、利率期限结构与宏观变量之间的动态关系。DRA模型虽没有无套利限定,但对许多国家的国债数据拟合较好,样本内和样本外预测表现均较佳;而且比起无套利模型,DRA模型不仅能考察宏观经济变量对收益率曲线的单向关系,而且还能考察收益率曲线对宏观经济变量的反向作用(吴吉林,2010)[24]。另外,多数应用DRA模型的文献,如Diebold等(2006)[7]、Lange(2013)[17]、王雪标和龚莎(2013)[26]等,是采用kalman滤波估计出潜在因子序列,再将其与宏观变量观测值序列一起构建VAR模型,这一作法只能对不可观测变量进行优化,而无法对其他宏观经济变量进行优化求解。为此,本文参考Chen-Scott(1993)[4]、Favero, Niu, Sala(2007)[3]的做法,采用极大似然估计方法求解包含国债供求变量的DRA模型参数,该方法利用样本数据的所有信息对不可观测变量和宏观经济变量同时进行优化求解,提高了模型的预测精度。
计量模型与检验方法
DRA模型可简单表示成动态Nelson-Siegel模型和VAR模型两个部分。其中,动态Nelson-Siegel模型从多个期限的利率时间序列中抽取出可以反映整个利率期限结构动态变化的三个潜在因子(β1t、β2t、β3t),如下式:
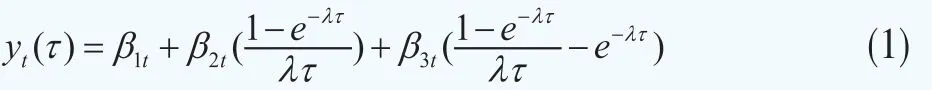
其中,τ为到期期限;β1t、β2t和β3t分别为水平因子、斜率因子和曲度因子。一般认为,水平因子代表利率的整体水平;斜率因子则对应着利率期限结构曲线的斜率,可以用短长期利差来表示;而曲度因子则主要与利率波动率有关。λ∈[0,1]为衰减率,λ越小,载荷衰减越慢,模型越适应期限较长的利率时间序列。为了考察利率期限结构与宏观变量之间的关系,DRA模型将三个潜在因子(β1t、β2t、β3t)与宏观变量一起组成状态因子向量xt,并假设其服从一阶向量自回归VAR过程。本文在宏观变量的选取中除了选用经济增长率gt,通货膨胀率πt和银行间同业拆借加权平均利率rt之外,还引入金融机构存贷比(Loan Balance,Lt)和银行间市场流通国债总额(Tradable bonds,TBt),用以分别描述国债需求1和供给两大因素,进而有xt=(β1t,β2t,β3t,gt,πt,rt,Lt,TBt),引入国债供求变量情况下的VAR模型2可表示为:

简记为:
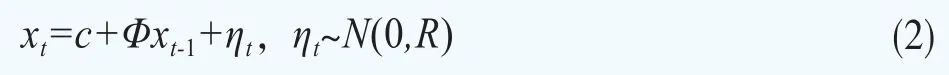
其中ηt为误差项,服从均值为0,协方差矩阵为对称矩阵R的多元正态分布3。本文为了理清潜在因子和宏观经济变量之间的相互影响关系,将待估计的转移系数矩阵Φ分为四部分:
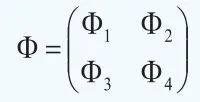
其中,Φ1为3×3矩阵,反映滞后一期潜在因子对当期潜在因子的影响;Φ2为3×5矩阵,反映滞后一期宏观变量对当期潜在因子的影响;Φ3为5×3矩阵,反映滞后一期潜在因子对当期宏观变量的影响;Φ4为5×5矩阵,反映滞后一期宏观变量对当期宏观变量的影响。
由于本文选用的数据是期限为12、24、36、48、60、72、84、96、108、120个月的利率时间序列,进而到期期限τ=12, 24, …, 120分别对应此时(1)式表示的动态NS模型的矩阵形式为:

此时模型(3)中的系数矩阵为:

其中,Ω前三列为三个潜在因子的载荷,后面几列均为零,以保证利率期限结构动态特征完全由三个潜在因子来反映。(2)式和(3)式构成了完整的DRA模型:此模型中,宏观经济变量与利率期限结构潜在因子在VAR框架内相互影响,其方向和程度主要通过模型(2)中的转移系数矩阵Φ得到体现。其中,Φ最后两行的系数反映了滞后一期潜在因子和宏观变量对当期国债需求变量Lt和供给变量TBt的影响,而最后两列的系数则反映了滞后一期国债供求变量对潜在因子和宏观变量的影响。
为了使用极大似然估计法对上述模型中的各参数c,Φ,R,λ,V进行估计,我们假设有三个期限的利率没有误差,而其他期限的利率存在误差,并且该误差服从正态分布。之所以这样设定是因为似然函数的构建主要基于可观测变量的概率分布,在DRA模型中却同时存在可观测变量和不可观测变量,为此需要把不可观测的潜在因子转化为可观测的利率,于是假定三个期限对应的收益率曲线没有测量误差5。由于我国国债市场上流通的国债到期期限多为2~7年,且多数文献证明Nelson-Siegel模型对短期和中期收益率拟合和预测效果较好,因此本文假设不存在测量误差。

其中

由(4)得xt=P-1Zt代入(2)式化简可得:

其中,δ=Pc,Ψ=PΦP-1。参照(3)式,含测量误差的各期限利率yet=,可表示为:
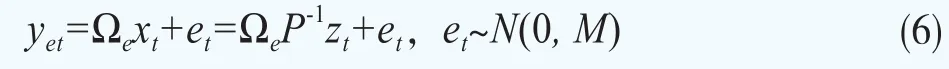
Ωe为Ω去掉第1、第3和第5行外组成的矩阵。
令It-1为所有可观测变量在t期前的观测值信息集,可得如下似然函数表达式:
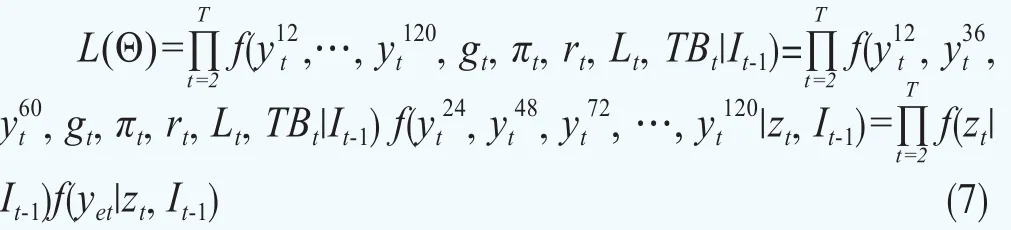
其中Θ包含了待估计参数c,Φ,R,λ,M。根据(5)式和(6)式可知:

因此,由多元正态分布的概率密度分布函数,对数极大似然函数可写为:
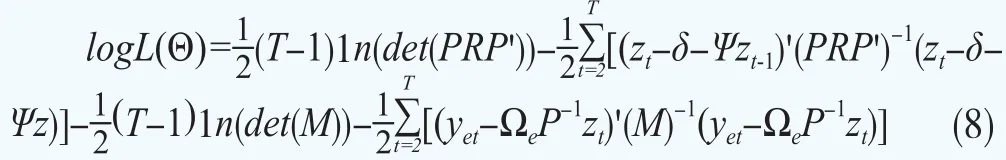
实证结果及分析
一、样本选取
本文使用2008年1月~2015年12月的月度数据,共96个月6。其中,国债利率使用期限为12、24、36、48、60、72、84、96、108、120个月的银行间固定利率国债收益率曲线数据。宏观经济变量中,经济增长率gt用GDP同比增长率代表7;通货膨胀率πt用居民消费价格指数(CPI)的同比变动率来衡量;货币政策变动rt用银行间同业拆借加权平均利率来反映;参考Fan et.al(2013)[9]的作法,采用金融机构人民币存贷比率表示国债需求因素Lt;由于实际国债流通总额受国债不断发行的影响,存在随时间增长的趋势,因此我们采用HP滤波的方法得到去除时间增长趋势后的国债流通总额TBt作为反映国债供给总量的指标。
国债收益率数据、银行间市场国债流通总额和金融机构人民币存贷款数据来自wind数据库,其他变量均来自中经网统计数据库。
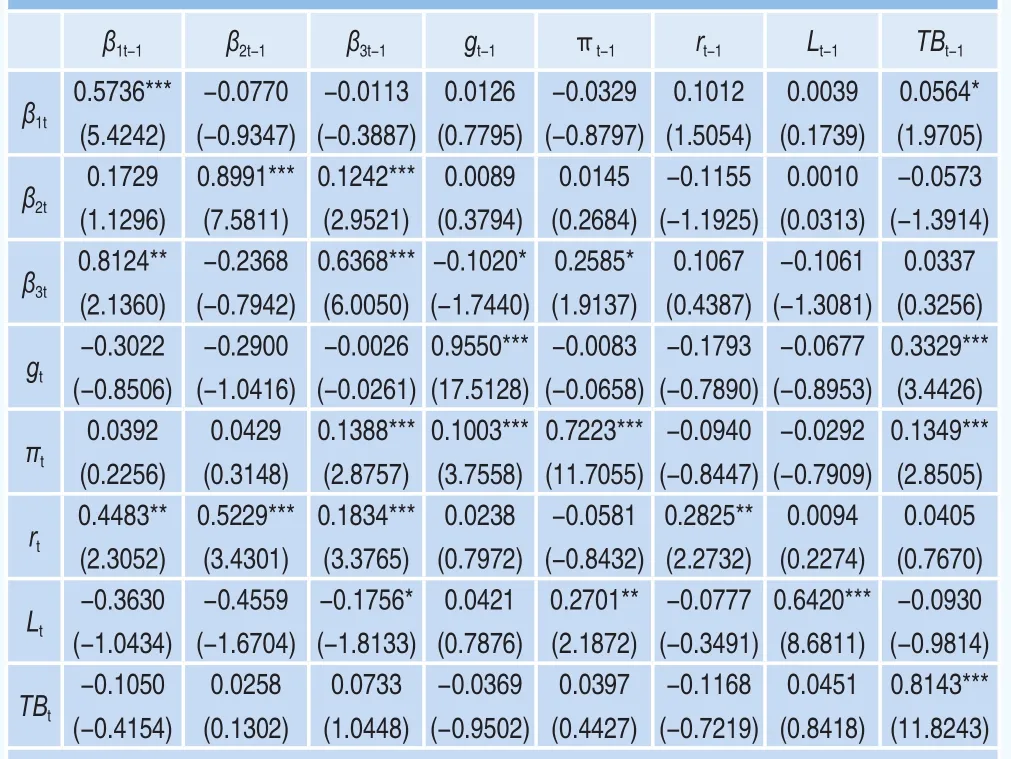
表1 转移系数矩阵Φ参数估计
二、实证结果及分析
1. DRA模型估计
本文参考曾耿明和牛霖琳(2013)[31]的作法,采用极大似然值的海塞矩阵估计参数的标准误差。表1列示了在引入国债供求变量情况下,VAR模型中转移系数矩阵Φ的估计结果。由表1可知,矩阵Φ的特征根均在单位圆内8,表明VAR模型是稳定的,同时表明国债利率期限结构存在均值回复现象。另外,矩阵Φ对角线元素大部分均在1%水平下显著,说明β1t,β2t,β3t,gt,πt,Lt,和TBt具有持久的自回归效应。为更好地分析矩阵Φ的非对角线元素的情况,我们按前文的作法,将转移系数矩阵Φ分为左上(Φ1)、右上(Φ2)、左下(Φ3)和右下(Φ4)四部分。
我们重点观察宏观经济变量与利率期限结构潜在因子之间的交互效应。在矩阵Φ的右上角(即Φ2部分)中,国债流通总额TBt-1前的系数为0.0564,且在10%水平下通过显著性检验,说明国债流通总额对水平因子β1t有显著正向影响,其原因是国债流通总额的正向变动意味着国债供给增加,国债价格下降,从而利率水平上升,这与韩国文(2016)[34]中供给因子能够对所有期限利率产生显著正向影响的实证结果一致;经济增长率gt-1对曲度因子β3t有显著负向影响;通货膨胀率πt-1对曲度因子有显著正向影响,影响系数分别为-0.102和0.2585。这表明,经济增长率与国债利率的波动程度呈反向变化特征,意味着当经济持续向好时,金融市场中的不确定性和风险会相对降低,此时国债利率的波动程度会有所减缓,反之亦然;而通货膨胀程度与曲度因子呈现同向变动特征,说明当经济处于通胀时期,金融市场的不确定性程度和风险增加,导致国债利率的波动程度增加,反之亦然。同理观察矩阵Φ的左下角(即Φ3部分),发现三个潜在因子都对银行间拆借利率rt有显著正影响,并且曲度因子分别对通货膨胀率和金融机构人民币存贷比Lt有显著正向和负向影响。这说明国债利率的波动程度增加,通常处于经济扩张时期,此时市场对于国债的需求会发生下降,将货币投入到扩大生产的过程,从而导致通货膨胀率出现正向的变动。矩阵Φ的右下角(即Φ4部分)揭示了各宏观变量之间的相互影响。除了对角线上的元素数值都较大,反映出经济增长率、通货膨胀率和国债供求因素都具有较高的持续性之外,国债流通总额对经济增长和通货膨胀有显著正向影响,系数分别为0.3329和0.1349,可以解释为国债供给增加往往伴随着政府扩大债务规模、加大财政支出,进而导致经济增长率和通货膨胀率的增加;而通货膨胀率对金融机构存贷比有显著正向影响,反映出通货膨胀率增加时期,政府会紧缩银根,提高资金成本,抑制信贷过快增长,由此使得存款上升的幅度高于贷款增加的幅度,导致金融机构存贷比上升。
2. 脉冲响应
由于向量自回归模型(2)的误差项的协方差矩阵R为非对角矩阵,所以我们使用cholesky分解进行脉冲响应分析,以避免相关变量间的交叉干扰。xt中各变量的顺序是:水平因子β1t、斜率因子β2t、曲度因子β3t、经济增长率gt、通货膨胀率πt、银行间同业拆借加权平均利率rt、金融机构存贷比Lt、银行间市场流通国债总额TBt。由此考察潜在因子、宏观经济变量和国债供求因素受到相互独立的外来冲击后,一些关键期限利率的脉冲响应。
由图1可知,水平因子冲击下,各期限收益率响应程度相似,均从1开始逐渐衰减到0附近,并且随着到期期限的增加衰减速度越快;斜率因子冲击下,到期期限越短的收益率曲线响应程度越大,且衰减速度越慢;曲度因子冲击下,各期限收益率的响应与斜率因子冲击下的响应模式类似,但衰减的速度较慢。上述分析均与吴吉林(2010)[24]的研究结果一致。在经济增长率的冲击下,利率期限结构的响应先下降后上升,并且随着到期期限的缩短,收益率响应幅度越大。王雪标和龚莎(2013)[26]采用工业增加值作为经济增长率的度量指标也取得了类似的结论。在通货膨胀率的冲击下,总体来说利率期限结构的响应为正,到期期限越长的收益率响应幅度越小;在银行间同业拆借加权平均利率冲击下,利率期限结构的响应幅度基本相同,但随着到期期限的缩短,衰减速度越慢。这两项响应的方向也与吴吉林(2010)[24]的研究结果一致。在金融机构存贷比(国债需求)增加的冲击下,利率期限结构的响应为负,且随着到期期限的增大,收益率响应幅度越小,并且衰减速度增加,这与张雪莹(2014)[22]所得到的国债需求变量与各关键期限国债利率明显负相关的结论一致;银行间市场流通国债总量冲击下,利率期限结构的响应为正。韩国文(2016)[34]基于我国数据的研究也得到类似的结论,他发现债券供给因子能够对所有期限即期收益率产生显著的正向影响。
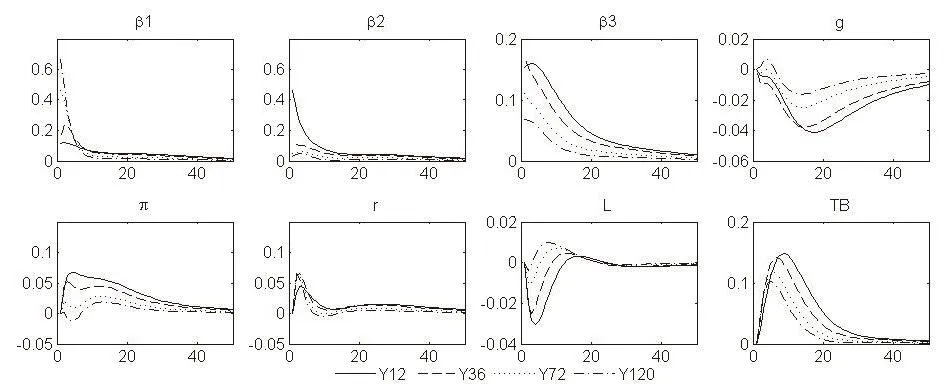
图1 潜在因子、宏观变量单位cholesky正向脉冲——利率期限结构响应
3. 方差分解
方差分解是通过分析潜在因子、宏观经济变量和国债供求变量受到外来冲击时对利率期限结构预测误差的影响,进而比较对收益率曲线产生影响的每个随机扰动的相对重要程度。表2给出了具有代表性的12个月、36个月、72个月、120个月期限利率的方差分解结果。
表中h表示超前预测期限,预测期限为1的各列反映了潜在因子、宏观经济变量和国债供求变量变化在受到一单位外来冲击的当期,对各期限利率方差的贡献程度;预测期限为12,36,60的各列则分别表示各因子在受到外来冲击一年、三年和五年后对各期限利率方差的贡献程度占比。总的来看,对于各期限利率,无论预测时间长短,水平因子和曲度因子对利率方差的贡献一直占主导地位;经济增长率、同业拆借利率、国债需求等变量对各期限利率方差的贡献率较低,尤其是国债需求变量,在Fan, Li and Zhou(2013)[9]中作为国债需求变量的银行存贷差的贡献也很小,他们认为一个可能的原因是需求因素与收益率曲线的斜率因子高度相关,其影响大部分被两个潜在因子所吸收;而随着利率期限的增加,国债供给变量对利率方差的贡献率呈现非单调的变化,都超出了其它宏观变量对利率方差的影响。例如,根据预测时间长短的不同,国债供给变量冲击对一年期利率y12方差的贡献率仅在0.17~0.19左右,而对三年期利率y36、六年期利率y72为0.24、0.26左右,但对十年期利率y120的方差贡献率则下降到0.23左右,这表明在利用宏观金融模型研究我国利率期限结构的变化时,不应该忽视国债供给因素的影响。这一结果与Dai and Philippon(2006)[5]以美国数据进行的研究相类似,该文发现国债供给冲击对十年期收益率预测误差方差的影响占13%。Canlin Li and Min Wei(2013)[2]也发现国债供给因素对于十年期收益率的贡献度是15%,对于五年期收益率的贡献度是6%,该文进而提出:为了更准确地对长期债券进行定价,对政府债务状况的重视程度应该超过通货膨胀率和实体经济等宏观变量。
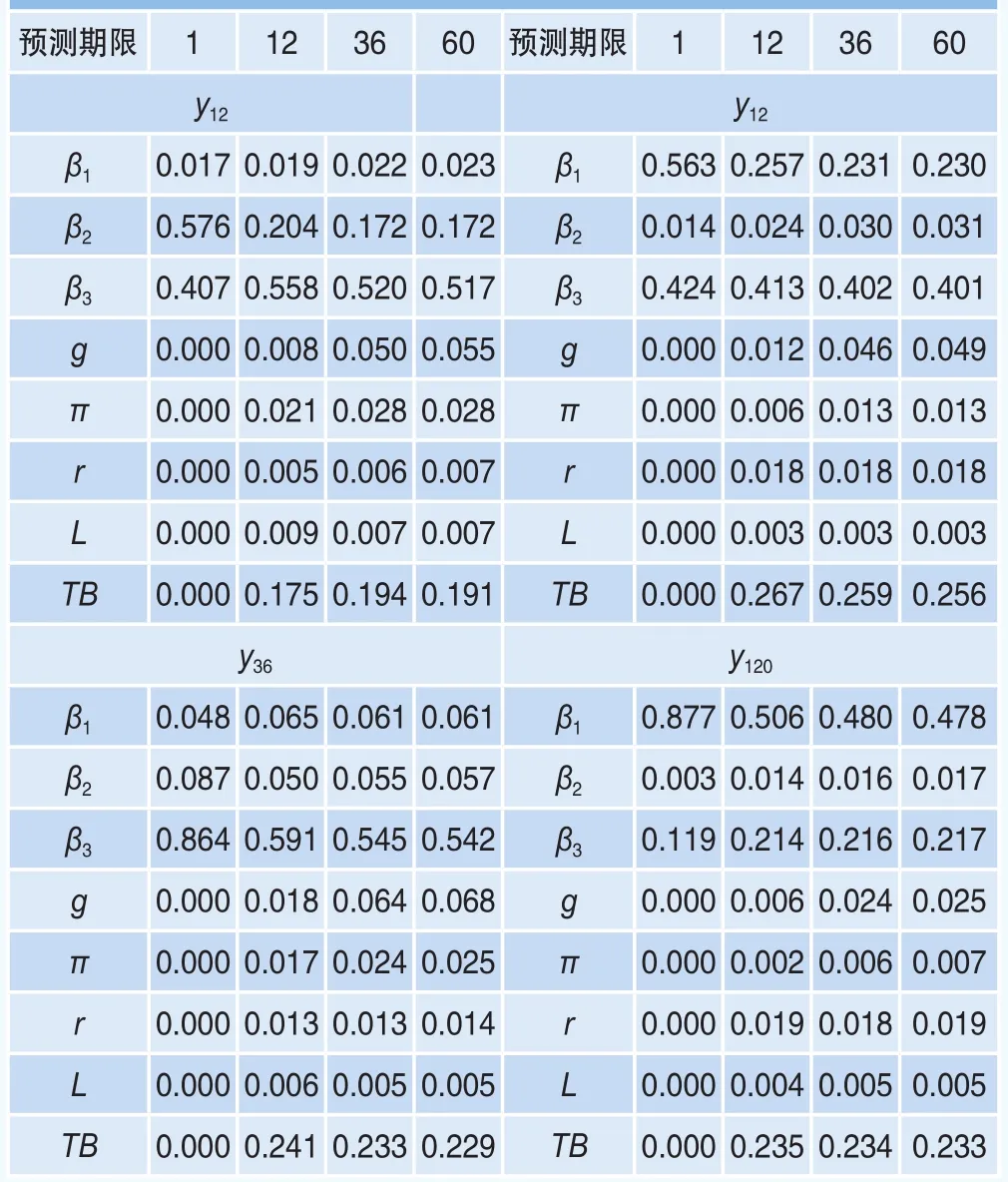
表2 部分关键期限利率的方差分解
结论和思考
本文运用DRA模型对国债供求因素、宏观变量与利率期限结构之间的动态交互关系进行研究。实证结果表明:(1)国债供给变量对利率期限结构的水平因子、经济增长和通货膨胀都有显著的正向影响;而利率期限结构的曲度因子对国债需求有显著负向影响;通胀率的上升则会导致国债需求的增加。(2)脉冲响应分析发现:在国债需求增加的冲击下,各期限利率的响应为负;而国债供给增加的冲击下,各期限利率的响应为正。(3)方差分解显示,国债供给变量对中长期国债利率方差的贡献率较大,而国债需求等变量对各期限利率方差的贡献率均较低。总的来看,国债供给因素对于我国利率期限结构具有显著的影响。
上述实证结果不仅在理论上有助于我们更准确地了解利率期限结构动态变化的微观机理,增进对利率期限结构与实际经济活动、货币政策之间相互关系的认识,提高利率期限结构预测模型的准确性;从实践上还有助于分析近些年来日益显现的政府债务管理与货币政策之间的冲突现象。例如,Hamilton and Wu(2012)[12]、Meaning and Zhu(2012)[16]的研究显示:面对高赤字政府债务危机的压力,政府债务管理者增加中长期国债发行的操作会与中央银行通过增加中长期债券需求以降低中长期利率的非常规货币政策发生冲突。长期国债供给量增加导致10年期利率上升约7bp,这一幅度是央行实施“卖短买长”扭曲操作、引导长期利率下降效应的两倍。如果没有长期国债供给增加所带来的反向作用,那么美联储大规模购买国债的货币政策对长期利率的降低效果将更大。与大多数发达国家相比,我国目前的政府债务仍有一定举债空间。据财政部的数据显示,截至2015年末,包括地方政府或有债务在内,全国政府债务占GDP的比重为41.5%左右,仍低于当前主要发达国家和新兴市场经济体的债务水平。在这一背景下,政府债券供给增加对利率期限结构、进而货币政策的影响、以及在加强政府债务管理政策与货币政策的协调配合等问题,将值得深入探讨。另外,管理层还需采取措施进一步完善我国国债发行市场的期限结构,提高国债交易市场的流动性。目前,我国短期国债的供给相对不足,市场的流动性较低,使得短期利率受国债供给冲击影响较大。增加短期国债的发行可以为公开市场操作提供更加充足的工具,使得国债收益率曲线对货币政策的反应更加灵敏、可靠。在这方面,财政部已经从2015年第四季度开始,按周滚动发行3个月记账式贴现国债。在增加国债二级市场流动性方面,我们需要加紧培育机构投资者,完善国债二级市场做市机制,增强其报价作用等。
[基金项目:国家自然科学基金项目“政府债务对货币政策的影响-基于利率传导渠道的研究”(71573155),山东省金融产业优化与区域发展管理协同创新研究(14xtzd09)]
注释
1.Fan, Li and Zhou(2013)从商业银行资产配置的角度,选择银行存贷比作为反映债券需求的指标,银行存贷比越高,银行可用于购买国债的资金越多。Krishnamurthy and Jorgensen(2015)发现:国债需求对信贷需求有挤出效应,受国债收益率变化的影响,银行资金配置国债需求的增加,往往伴随着银行信贷的下降、进而存贷比的上升。
2. 本文选择滞后一阶VAR模型,是因为作为DRA模型中的转移方程,VAR模型不能直接含有二阶(含)以上的滞后变量,必须重新定义状态向量。而且滞后阶数较多时,待估计参数过多,影响估计量的有效性。
3. 文章假定R为对称矩阵,即允许各潜在变量和宏观变量间的冲击可以相互影响。例如央行货币政策的变动,不仅会使银行间同业拆借利率,也会导致经济增长率和通货膨胀率的变化。且似然比检验结果显示该设定形式合理。
4. V取为对角矩阵,正如好多无套利模型都设定收益率模型的误差项是独立同分布的,即不同到期期限收益率的误差项不相互影响。
5. 没有测量误差表示收益率的变动完全可由潜在因子通过动态NS模型来反映,对应的误差项确定为零。
6. 数据显示银行间债券市场的国债流通总额在2007年末出现快速增长,且2007年中国人民银行发布《全国银行间债券市场做市商管理规定》正式建立了做市商制度,提高了国债市场的流动性。
7. gt=ln(GDPt/GDPt-12),其中GDP数据采用三次样条插值法对GDP季度数据进行了月度分解,再用X-12方法进行季节调整。
8. 转移矩阵特征根

0.957 0.828 0.828 0.817 0.428 0.428 0.695 0.563

