误差量测与杂波环境对水下目标跟踪的影响分析

李冬冬 ，张 瑶 ，林 扬

（1.中国科学院沈阳自动化研究所机器人学国家重点实验室，辽宁 沈阳 110016；2.中国科学院大学，北京 100049）

误差量测与杂波环境对水下目标跟踪的影响分析

李冬冬1，2，张 瑶1，林 扬1

（1.中国科学院沈阳自动化研究所机器人学国家重点实验室，辽宁 沈阳 110016；2.中国科学院大学，北京 100049）

在水下特殊的环境中，大误差量测与强杂波环境会对目标跟踪有显著的影响。量测误差越大，则预测门限区域越大，杂波密度越高，那么轨迹更易于与杂波关联，进而降低正确量测的权重，滤波精度因此下降。文中依据量测误差模型与杂波模型，建立了误差量测与杂波对水下目标跟踪的影响模型。依据该模型可定量分析量测误差与杂波对目标跟踪的影响，可为目标跟踪滤波器提高抗杂波能力或者提高滤波精度提供理论依据。

目标跟踪；大误差量测；强杂波环境；阈值；理论分析

现如今，目标跟踪遍及生产生活的各个方面，如民用领域中空中交通管制与视频监控系统，军用领域中运动目标的预警与火力控制等[1-4]。随着科学与技术的进步，越来越多的财力与物力投入到目标跟踪领域，目标跟踪理论与技术得以迅速发展。但无论是军事还是民用研究，就水下特殊的环境而言，如大误差量测和强杂波环境，目标跟踪依旧是一个非常重要的研究领域，仍有许多关键而且迫切的问题尚未解决[5-8]。

就目标跟踪而言，水下环境的特殊性在于：（1）量测误差大；（2）声纳探测频率低；（3）海洋环境杂波多。

量测误差大，是指相对于目标的运动因素，传感器量测因素不可以忽略。量测误差大，导致门限区域变大，致使更多的杂波落入门限区域内，进而降低轨迹与正确量测关联的概率，从而导致目标跟踪精度下降，尤其是在跟踪距离较远的目标。

声纳探测频率低，是单位时间内获得目标的数据信息少。在空气中，雷达可以以高频率获得目标的量测信息。水下声学探测系统存在着探测时延大，探测频率低，也即单位时间内可获得的目标数据信息量少。那么，相对于雷达而言，其需要更长时间才能获得更准确、更确定的水下目标信息[9]。

海洋环境杂波多，即强杂波环境，指环境中存在不可忽略的类似目标的量测，在目标跟踪过程中，会降低目标轨迹与正确量测关联的概率，进而降低滤波精度。

就本文而言，仅仅讨论大误差量测与强杂波环境对目标跟踪的影响，并为目标跟踪提供参考依据。当然还有其他环境因素或者传感器因素也影响目标跟踪效果，如探测目标传感器单一，水下通信困难，不利于组网等[10]，但这些因素在此文中暂不考虑。

此文章的组织结构如下：在第1节详细介绍误差量测，以及其对目标跟踪的影响；在第2节详细介绍杂波环境，以及其对目标跟踪的影响；在第3节通过仿真分析误差量测和杂波环境对目标跟踪的影响；在第4节，总结全文。

1 误差量测

量测误差反应了传感器对目标的量测精度，大误差量测是指传感器的量测因素相对于目标的运动因素，对目标状态的估计存在不可忽略的影响。文献[11]详细介绍了在航迹起始阶段，量测因素与目标运动因素之间的关系，并且大误差量测如何影响航迹起始性能的。但其中有两个关键的问题尚未解释清楚：（1）如何定义大误差量测环境；（2）如何确定航迹起始阶段与目标跟踪阶段的门限。

1.1 大误差量测环境

本小节阐述如何定义大误差量测环境。大误差量测可解释为在目标的速度方向上，前后两帧的量测区域有大面积重叠。如图1所示，红色点是目标的真实但是未知的状态，绿色点是目标含有误差的量测点，数字表示时间，大圆圈表示目标的有效量测区域，空心箭头表示目标的真实运动方向，实心箭头表示目标的初始估计值 (箭头长度代表估计速度大小，箭头方向代表估计速度方向)。由图1可知，当两个量测区域相距越远 (重叠区域越小或无重叠区域)，即量测误差因素相对于运动因素越小，目标的初始估计值越准确；当重叠的量测区域越大，即量测误差因素相对于运动因素越大，则初始估计值误差越大。因此在目标跟踪过程中，首先应该确定是否是大误差量测环境。

假设T是采样周期，vmax是目标的最大速度，σRmin是量测协方差矩阵R^k的短轴长，如果不等式(1)成立，则表示属于大误差量测环境。下文介绍式(1)的推导过程。

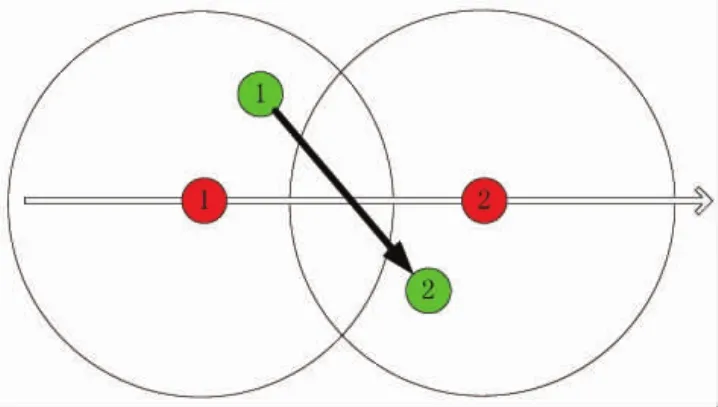
图1 量测因素与目标运动因素对初始状态估计的影响

图2 沿着速度方向量测1标准差与量测协方差矩阵1标准差的关系

假设在二维平面对目标进行跟踪并分析量测分布特征，如图2所示，在某时刻目标的量测分布图，图中椭圆为量测协方差矩阵的1标准差分布图。则沿着速度方向的量测分布1标准差是介于长轴与短轴之间，如式（2）：

考虑极限情况，可令 σv=σRmin，如果当 σv=σRmin时属于大误差量测情况，那么当速度方向改变时，同样也属于大误差量测情况。沿着目标速度方向，第k时刻目标的量测分布为：

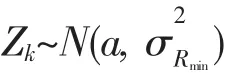
其中a为任意值，N(*,*)表示高斯分布，此时Zk为标量，第k+1时刻目标沿着速度方向移动最大位移的量测分布为

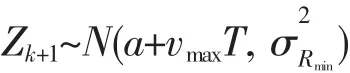
则

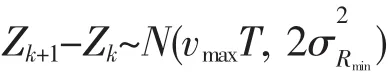
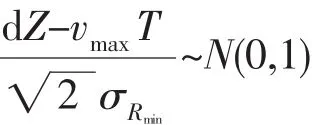
如果量测误差比较小或者目标的速度 (最大速度)比较大，则dZ＜0的概率很小，如果量测误差比较大，则dZ＜0的概率相对变大，dZ＜0的概率越大，则航迹起始阶段，对速度的估计误差越大，则dZ＜0的概率可衡量量测误差的大小。假设函数Φ(*)是标准正太分布的分布函数，则如果dZ＜0的概率大于Φ(-1)，可定义为大误差量测，即当

为了简化处理，可令

则依据高斯分布特征可得

即可得式(1)。依据标准正太高斯分布特征，则对应dZ＜0的概率

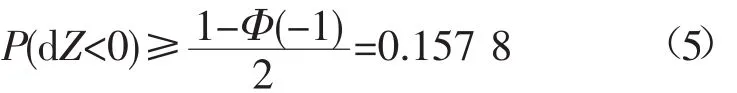
即当式(1)成立时，则估计速度的方向与目标真实速度的夹角超过90°的概率不小于0.157 8，此种情形定义为大误差量测环境。从式(1)可知，当速度(最大速度)越小，传感器量测误差越大，航迹起始对初始状态估计越困难；反之，越容易。由此可见大误差量测与目标的最大运动速度、传感器量测精度以及采样周期有关。

1.2 航迹起始阶段的门限

本小节阐述如何确定航迹起始阶段的门限，其为

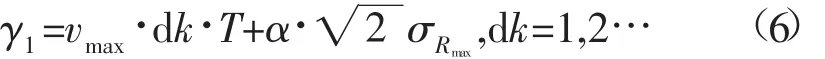
式中：γ1是预测区域的门限；σRmax是量测协方差矩阵Rk的长轴长；dk是两次关联扫描间隔次数；α是一个可调节的参数。假设在二维空间中，第k时刻目标的量测分布为：

式中：Zk为二维空间矢量；Ak是k时刻目标真实而未知的二维空间位置；R^k是二维量测标准差。则目标在以最大速度运动情况下，k+dk时刻目标量测分布为：

其中为了简化处理，可令R^2k+dk=R^2k，并且

‖*‖2表示向量的2范数。则

为了简化处理，可令

γ1的意义在于其所确定的区域内，使目标第k帧与第k+dk帧量测相关联的概率不小于概率P1，即

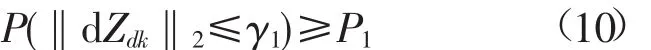
如图3所示，描述γ1与目标运动因素、量测因素的关系，以及dZdk的分布图。其中黑色椭圆是以Vma·T 为圆心，1 标准差是 2R^2k的分布区域，即黑色椭圆包含dZdk的概率0.393 5。红色点线椭圆是包含dZdk概率为0.9的区域。其概率P1与α倍标准差之间的关系为

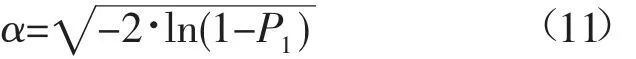
式(10)指明γ1所确定的圆形区域是以原点为圆心，γ1为半径，以不小于概率P1包含dZdk的区域。结合图3，并适当简化分析，当时，则可使γ1所确定的区域包含dZdk的概率不小于P1。其中vmax·dk·T反应目标的运动因素，反应传感器的量测性能以及概率要求。至此，式(6)证明完毕。

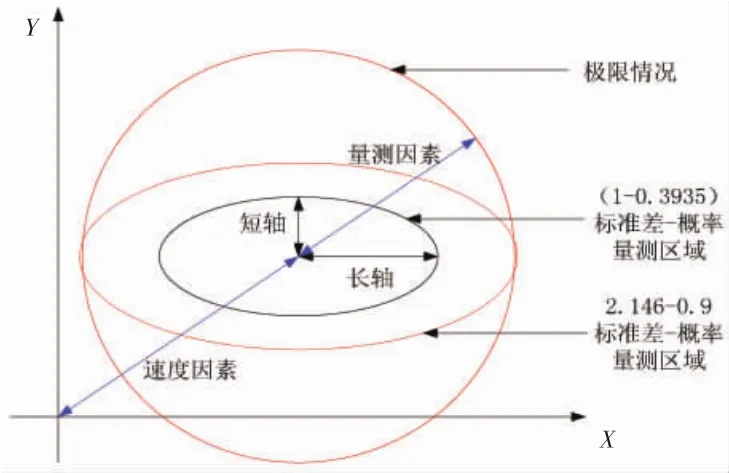
图3 依据目标的速度因素，传感器量测因素以及概率要求确定门限大小

1.3 目标跟踪阶段的门限

当处于跟踪阶段时(目标轨迹已经确认，并且目标状态经过合理地初始化赋值)，预测门限定义为

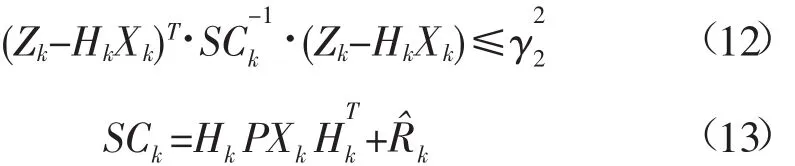
式中：Zk是声纳在第k时刻的量测；Hk是第k时刻的量测矩阵；Xk是第k时刻的目标状态；SCk第k时刻的新息协方差矩阵。γ2则对应于预测区域的门限。调节γ2也可依据式(11)来确定，即

P2是γ2对应的区域包含预测量测的概率。

门限γ1所确定的区域，则以P1的概率包含预测量测，即假如P1值为0.9而且目标被检测到，那么下一时刻目标的量测以0.9的概率落入到由式(6)和(11)所确定区域。即P1赋予所确定区域的置信度。同理，γ2与P2之间的关系也是如此。

由式(6)和(12)可得，无论是在航迹起始阶段还是在目标跟踪阶段，门限均与传感器量测精度有关。传感器量测精度越高，量测协方差矩阵R^k越小，σRmin和σRmax越小，则门限区域越小，此时杂波落入区域的概率越低，而门限区域包含源于目标量测的概率保持不变，以此提高目标跟踪的估计精度。

1.4 量测无偏转换

在实际声纳应用环境中，声纳获得目标在2维空间中的距离和角度信息，同时也包含环境中的杂波。一般情况，没有额外的量测特征信息区分杂波与目标量测。源于目标的量测仅仅取决于目标当前的状态，并服从高斯分布，如下式：

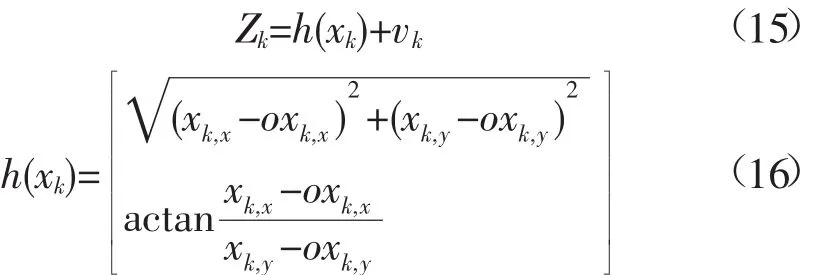
在量测方程中，量测量与状态量之间的函数关系往往建立在极坐标系下，然而在多数系统中，目标运动模型往往建立在直角坐标系下。此种情况要么将极坐标量测转化为直角坐标系下的量测，然后在直角坐标系下，采用伪线性滤波方法处理状态与量测关系。要么在混合坐标系下，采用非线性滤波方法[12]。为了简化分析，我们采用前一种方法，首先进行无偏转换，即首先将极坐标系下的量测转化为直角坐标系下的量测，如下式

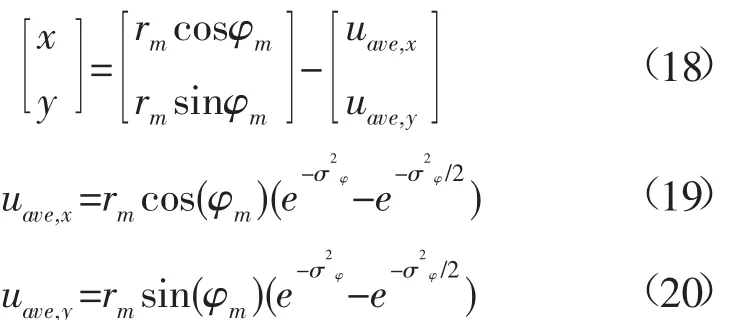
其中：Zk=[x,y]T是无偏转换之后直角坐标系下的量测；(rm，φm)是声纳传感器极坐标系下的量测；(σr,σφ)是极坐标下的距离量测标准差和角度量测标准差；[uave,x，uave,y]T是转换偏差。

经过量测转换之后，式（15）～式（17）可简化为线性量测方程，如下式：

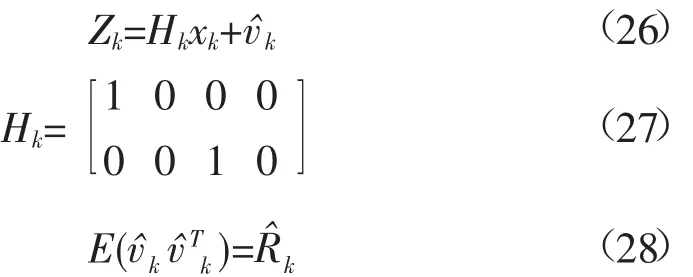
由于传感器量测的精度往往与量测距离成正比，因此，距离传感器较近的量测属于高精度量测，距离传感器较远的区域属于大误差量测。例如，声纳可以探测目标的距离和角度信息，其中距离标准差是声纳与目标真实距离的0.015倍，角度标准差是1°，因此距离目标越远，其量测协方差矩阵越大。因此对于声纳探测轴线上的目标，由近到远，会依次出现探测精度高到探测精度低的过程，即大误差量测不仅仅与目标的速度，传感器精度有关，还间接地与目标到传感器的距离有关。

2 杂波环境

杂波密度反应目标跟踪背景环境的统计特征[13]。杂波密度λ定义为传感器有效观测区域A内杂波的平均个数，即：

杂波个数与位置分布均是随机变量，且仅仅取决于并反应当前环境统计特征。通常情况，杂波的个数服从泊松分布，即：

其中 pm¯(*)是泊松函数。杂波的位置量测(xi,yi)在有效观测区域内服从均匀分布。

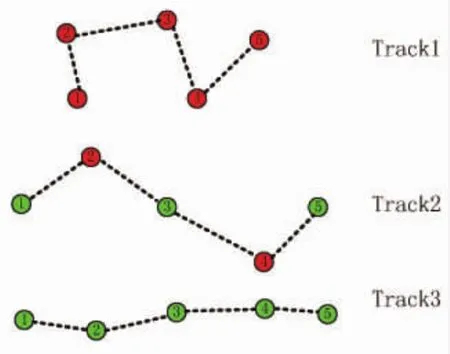
图4 轨迹中不同类型的量测图

在强杂波环境中，杂波对目标跟踪有不可忽略的影响。例如在航迹起始阶段，杂波密度过高会显著地增大航迹起始的困难程度，如图4所示，轨迹1的量测完全是由杂波构成；轨迹2中部分量测源于杂波，其他的源于目标；轨迹3的量测完全源于目标。轨迹1则属于虚警，会增加计算机负担，并且干扰跟踪者决策。轨迹2会恶化目标的初始化精度，因为其包含了一些杂波，因此轨迹2量测特征并不完全反应目标的运动特征。轨迹3才是跟踪者所希望的轨迹。强杂波环境会增加轨迹1和轨迹2的个数，减少轨迹3的个数。

在目标稳定跟踪阶段，强杂波环境会增加杂波对轨迹干扰，降低正确量测的权重，如图5所示。量测1、2和3位于有效预测区域内，滤波器会给与3个量测赋予不同的权值；其中量测2是源于目标的量测，其余的均是杂波。杂波密度越高，落入波门区域内的杂波个数越多，滤波器会对所有波门区域内的量测分配相应的权重，如此便稀释了正确量测的权重，进而降低了目标状态的估计精度，并且增加了计算量。

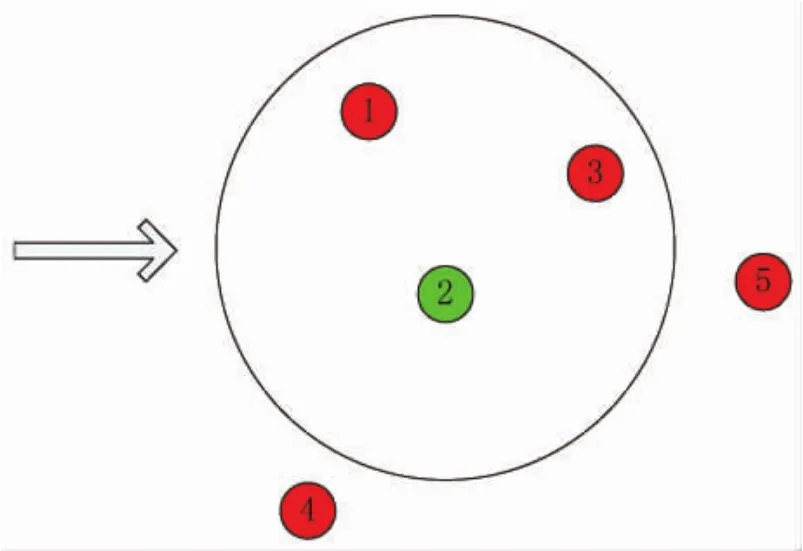
图5 强杂波环境在目标跟踪阶段情况

此外，强杂波环境与大误差量测的叠加效果会进一步增加目标跟踪的困难。量测误差越大，杂波密度越高，轨迹与量测的关联正确率就越低。比如，当没有量测误差时，无论杂波密度多高，我们均可以采用“点与点连线”方法进行数据关联，简单而且有效。但是如果存在量测误差，“点与点连线”方法就不再起作用，那么必须要考虑杂波与误差量测的共同影响。

3 仿真与分析

本文首次提出关联概率比的概念，来定量描述量测误差与杂波对目标跟踪性能的影响。分别针对航迹起始阶段与目标跟踪阶段，结合仿真与分析，阐述关联概率比。

3.1 航迹起始阶段的关联概率比

在航迹起始阶段，如式(6)所确定的预测区域内，定义出现正确量测的概率与出现杂波的概率之比为关联概率比β，用来衡量杂波与量测误差对目标跟踪的综合效果，其表达式为

依据式(6)，(11)，(29)和(30)可得

在航迹起始阶段，单独考虑量测误差对目标跟踪的影响。如图6所示，当杂波密度不变λ=2.3×10-6，量测误差由0～300 m变化时，关联概率比随量测误差的变化情况 (量测误差的大小等价于量测协方差矩阵的长轴长)。当不存在量测误差时候，或者如果目标距离声纳非常近，在航迹起始阶段所确定的门限内，潜在轨迹被正确量测更新的概率大约是被杂波更新概率的8倍，如果量测误差比较大(长轴长为157 m，也即在9 000 m探测边界处)被两者更新的概率几乎相等。当量测误差继续增大，那么关联概率比则稳定在0.81附近，不再衰减。此外从图6中可以看出，当量测误差在0～150区间段内，量测误差变大时，其关联概率比是成指数衰减的。这说明，如果在距离声纳较近的位置，提高传感器量测性能，会显著提高关联正确率，进而提高航迹起始性能。

图6 航迹起始阶段量测误差对航迹起始的影响效果图

如图7所示，在航迹起始阶段，关联概率比随杂波密度之间的关系。与关联概率比随量测误差之间的关系相类似，随着杂波密度的增加，概率比以指数关系迅速减小，并且当杂波密度大于临界值0.000 005时，变化逐渐趋于稳定值0.81。此说明，当杂波密度小于临界值时，关联概率比对杂波密度的变化很敏感，需要慎重对待杂波密度的变化。而当杂波密度大于临界值，需要考虑杂波的影响，但不必关心杂波密度的具体值。

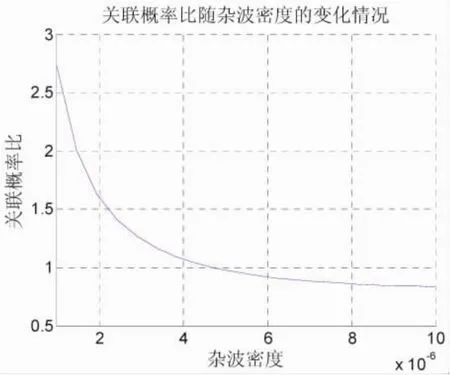
图7 航迹起始阶段杂波密度对关联概率的影响

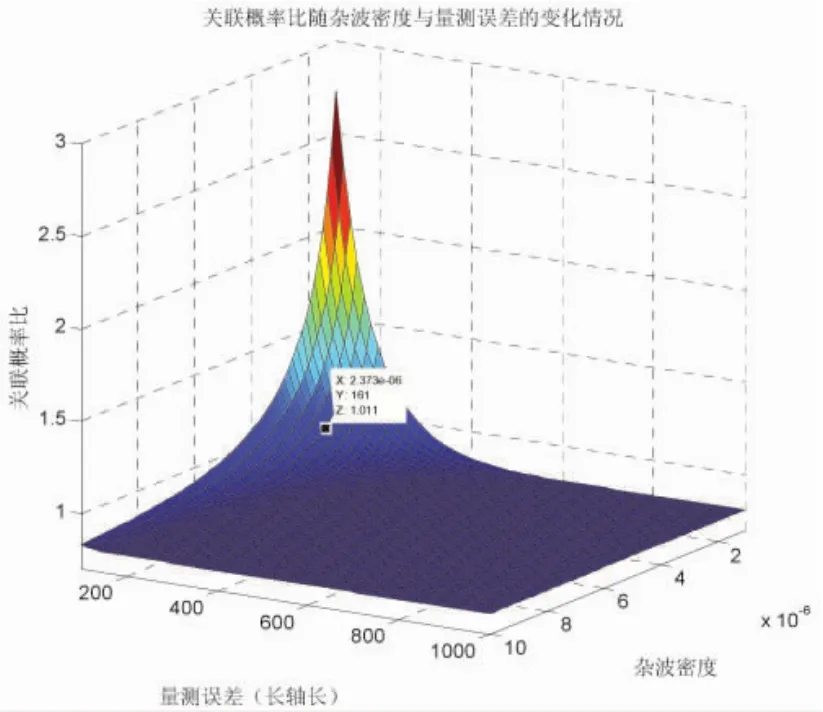
图8 航迹起始阶段概率比随杂波密度和测量误差的变化关系

如图8所示，关联概率比随着杂波密度与量测误差变化图。从图中可得当杂波密度为λ=2.37×10-6，量测误差长轴为161 m时，潜在轨迹被目标量测更新与被杂波更新的概率相等。λ=2.37×10-6相当于在声纳探测半径为9 000 m的范围之内杂波均值为603个，量测误差协方差矩阵长轴为161 m相当于目标正好在声纳的探测边界。结合图6～图7，也可知，概率比发生显著变化的区域是杂波密度在（2～10）×10-6之间，长轴在 0～80 m 之间。此外，从图 8的整体趋势可以得出，杂波与量测误差有正强化作用，会使航迹起始阶段的门限确定更加困难。

3.2 目标跟踪阶段的关联概率比

在目标稳定跟踪阶段，如式(12)所确定的预测区域内，也可以用关联概率比来衡量误差量测与杂波对目标跟踪的综合影响。依据式 (12)～式 (14),式(29)～式(30)可得：

由式(33)可得传感器对目标的检测概率、自定义的门限概率、环境特征以及传感器量测精度，影响关联概率比。相比航迹起始阶段，不再受目标运动因素，传感器采样速率也不直接影响关联概率比。为了简化分析，可令σRmin=σRmax。

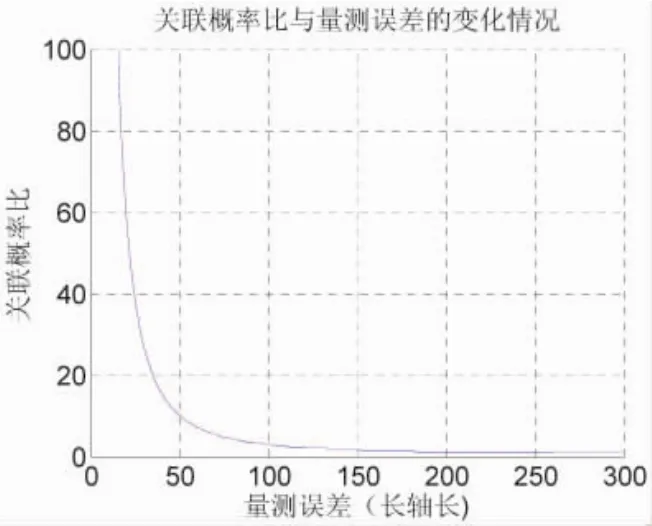
图9 跟踪阶段关联概率比随杂波密度和量测误差的变化关系

图9，当杂波密度不变λ=2.3×10-6，量测误差由0～300 m变化时，关联概率比随量测误差的变化情况。当不存在量测误差时候，或者如果目标距离声纳非常近(长轴长小于50 m)，目标跟踪阶段所确定的门限内，轨迹被正确量测更新的概率大约是被杂波更新概率的10倍以上，即此时几乎可以不考虑杂波的影响。如果量测误差比较大(长轴长＞100 m)杂波对概率比的影响显著增加，此时必须考虑杂波的影响，因为杂波参与滤波器更新过程的几率非常大。此外从图中可以看出，当量测误差变大时，其关联概率比是成指数衰减的。这说明，如果在距离声纳较近的位置(小于临界值100)，提高传感器量测性能，会显著提高关联正确率。

如图10所示，当量测误差不变时 (长轴长为100 m)，关联概率比随杂波密度之间的关系。其与关联概率比随量测误差之间的关系相类似，随着杂波密度的增加，概率比以指数关系迅速减小。

如图11所示，关联概率比随着杂波密度与量测误差变化图。从图中可得当杂波密度为λ=6×10-6，量测误差长轴为133.9 m时，潜在轨迹被目标量测更新与被杂波更新的概率相等。随后当杂波密度减小或者量测误差减小时，关联概率会迅速增大。结合图8，目标跟踪稳定阶段与航迹起始阶段的关联概率比变化有相似性也有区别。相似性在于整体趋势不变，区别在于，在同样的杂波密度和量测误差的情况下，稳定跟踪时的关联概率比要大于(甚至是远大于)航迹起始阶段的情况，由此可得，在航迹起始阶段更应该关注杂波密度变化与量测误差变化。

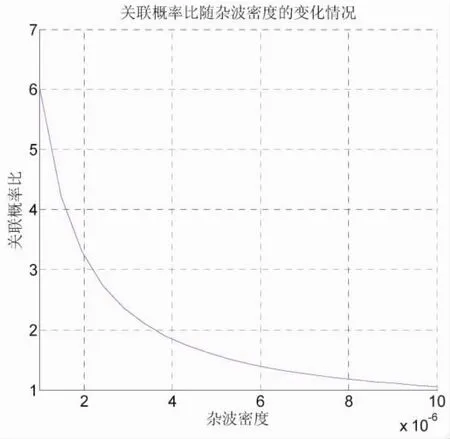
图10 跟踪阶段关联概率比随杂波密度的变化关系

分析量测误差和杂波密度对关联概率比的影响，可以指导对目标跟踪中关键参数的选择，比如在航迹起始阶段，采用基于逻辑的航迹起始方法，当杂波密度小于10-6几乎可以不考虑杂波的影响，依据此可以提高波门门限，进而增加目标的检测概率，尽快得到目标的轨迹，同时几乎不增加虚警概率[14]。再比如当处于稳定的目标跟踪阶段，采用概率数据关联方法对目标进行跟踪[15]，当量测误差长轴小于50 m时候(或者当目标距离声纳较近时候)，几乎不考虑杂波的影响，当长轴大于100 m(即当目标较远的时候)必须考虑杂波对滤波器的影响，或者慎重地考虑门限等相关参数的选择[16]。

图11 跟踪阶段关联概率比随杂波密度和量测误差的变化关系

4 结论

本文阐述了大误差量测与强杂波环境对目标跟踪的影响，为目标跟踪参数的确定提供依据。杂波环境与传感器量测因素对目标跟踪的影响有一个从量变到质变的过程，此可以从关联概率比(轨迹被正确量测更新的概率与被杂波更新的概率之比)的变化趋势得出。关联概率比越大，则表示目标跟踪环境越理想，可以选择较大的波门门限，来增加轨迹与正确量测的关联概率。如果概率比比较小，那么我们就要慎重考虑波门门限的选择，或者增加更多的传感器，获得目标更多的量测信息，如幅值信息，径向速度信息，去分辨杂波与源于目标的量测，进而提高关联正确率，增加对目标的滤波精度。

[1]M N V S S Kumar,N Modalavalasa,L Ganesh,et al.A new approach for tracking moving objects in underwater environment[J].Current Science,2016,110:1315-1323.

[2]D V A N R Kumar,S K Rao,K P Raju.A novel stochastic estimator using pre-processing technique for long range target tracking in heavynoise environment[J].Optik,2016,127:4520-4530.

[3]J Yan,H Liu,B Jiu,et al.Joint Detection and Tracking Processing Algorithm for Target Tracking in Multiple Radar System[J].IEEE Sensors Journal,2015,15:6534-6541.

[4]K D S Raj,I MKrishna.Kalman filter based target tracking for track while scan data processing[C]//Electronics and Communication Systems(ICECS),2015 2nd International Conference,2015:878-883.

[5]H Liu,H Liu,X Dan,et al.Cooperative track initiation for distributed radar network based on target track information [J].IET Radar,Sonar&Navigation,2016(10):735-741.

[6]M Mallick,Y Bar-Shalom,T Kirubarajan,et al.An improved single-point track initiation using GMTI measurements [J].IEEE Transactions on Aerospace and Electronic Systems,2015,51:2697-2714.

[7]王康,蒋志迪,张晴月.基于IMMKF-3D的水下目标跟踪算法[J].设计与实现,2016(16):73-79.

[8]伍锡如,黄国明,孙立宁.基于深度学习的工业分拣机器人快速视觉识别与定位算法[J].机器人,2016,38(6):711-719.

[9]邹吉武.多基地声纳关键技术研究[D].哈尔滨:哈尔滨工程大学,2012.

[10]朱光明.异步水下传感器网络目标跟踪算法研究[D].杭州：浙江大学，2015.

[11]LDongdong,ZYao,LYang,et al.Anovel track initiation method for track splittingand merging[C]//OCEANS2016,Shanghai,2016:1-7.

[12]S W Yeom,T Kirubarajan,Y Bar-Shalom.Best linear unbiased filtering with nonlinear measurements for target tracking [J].IEEE Transactions on Aerospace and Electronic Systems,2004,40：17-24.

[13]H L Kennedy.Powerful Test Statistic for Track Management in Clutter[J].IEEE Transactions on Aerospace and Electronic Systems,2014,50：215-223.

[14]HZhijian,HLeung,MBlanchette.Statisticalperformanceanalysisoftrackinitiationtechniques[J].IEEETransactionsonSignalProcessing,1997,45：445-456.

[15]H LKennedy.Comparison ofMHTand PDAtrack initiation performance[C]//2008 InternationalConferenceon Radar,2008:508-512.

[16]M S Aslan,A Saranli.Threshold Optimization for Tracking a Nonmaneuvering Target[J].IEEE Transactions on Aerospace and Electronic Systems,2011,47:2844-2859.

Analysis on the Influence of Measurement Errors and Clutter Environment on Underwater Target Tracking

LI Dong-dong1,2,ZHANG Yao1,LIN Yang1
1.State Key Laboratory of Robotics,Shenyang Institute of Automation,Chinese Academy of Sciences,Shenyang 110016,Liaoning Province,China;
2.University of Chinese Academy of Sciences,Beijing 100049,China

In the harsh underwater environment,large measurement errors and heavy clutter environment will certainly pose additional difficulties and challenges to underwater target tracking.The greater the measurement errors are,the larger the validation prediction area is,the heavier the clutter is,with target tracking being easier to associate with clutter,which will decrease the estimating accuracy.This paper presents the model of large measurement errors and heavy clutter environment affecting underwater target tracking based on the statistic characteristics of large measurement errors and heavy clutter.So it can quantitatively analyze the effect of large measurement errors and heavy clutter for improving the performance of filter or providing the theoretical foundation of target tracking.

target tracking;large measurement error;heavy clutter environment;threshold;quantitative analysis

P714

A

1003-2029（2017）05-0038-08

10.3969/j.issn.1003-2029.2017.05.007

2017-04-06

中国科学院科技创新重点部署项目资助（KGFZD-125-014）

李冬冬（1989-），男，博士，主要研究方向为水下目标跟踪、水下导航。E-mail:lidongdong@sia.cn