基于雷达测量数据的弹箭扰动源最优估计

丁传炳

（中国舰船研究设计中心，上海 201108）

基于雷达测量数据的弹箭扰动源最优估计

丁传炳

（中国舰船研究设计中心，上海 201108）

为精确计算舰载武器的飞行状态参数，以弹体纵向运动过程为研究对象，推导了包含误差干扰源在内的纵向扰动运动学方程，利用“系数冻结法”及拉普拉斯变换得到解析解，拟合出弹体被动段纵向运动的气动参数公式，采用三坐标雷达测量量作为系统量测方程，从而对气动参数误差干扰源进行最优估计。计算结果表明：该算法可以使俯仰操纵力矩系数导数误差的精度稳定在±0.007 (°)-1范围内，阻力系数误差的精度趋于±0.025之间；升力系数误差基本稳定在±0.12之间；俯仰力矩系数对攻角的导数偏差精度稳定在±0.011 (°)-1之间；俯仰阻尼力矩系数误差的精度收敛于±0.009 (°)-1之间，且算法收敛速度快，可为重构高精度的弹道参数提供支撑。

最优估计；纵向运动；扰动源；雷达

针对弹箭飞行状态参数最优估计问题，目前大多采取的方法是通过各种外弹道试验测量数据进行弹道滤波[1-3]。为了从源头上提高外弹道飞行状态参数的估计精度，本文提出采用雷达观测量来对气动系数误差干扰源进行最优估计，进而为重构高精度的弹箭飞行状态参数创造条件。考虑到有控飞行器的空间运动可以看成是铅直面内的运动与侧向平面内运动的合成，并且在许多情况下，主要是在一个铅直平面内的飞行，因此本文以弹箭纵向运动面为研究对象，运用三坐标雷达观测量对纵向气动参数误差干扰源进行最优估计，估计出来的高精度气动参数可为重构飞行外弹道最优状态参数提供数据支持。

1 纵向扰动运动方程

如果飞行器的气动对称面与铅直面重合，并且质心也在铅直面内运动，则称为纵向运动。对于制导控制系统工作正常的弹箭，其实际飞行运动参数也总在理想弹道运动参数附近变化，即弹箭受到控制或干扰产生的扰动可认为是加在理想运动上的小扰动，因此就可将实际运动参数看作是理想弹道运动参数与对应偏差量之和，因偏差量很小，故可将纵向运动方程在基准运动附近进行线性化，组成关于偏差量的线性运动方程[4-6]，即：

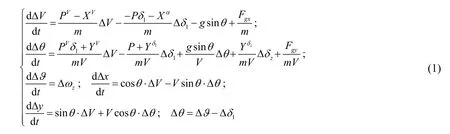
式中：Ρ表示发动机推力，V表示弹丸飞行速度，X表示阻力，Y表示升力，1δ表示攻角，δz表示升降舵偏角，m表示弹丸质量[6-8]。由纵向扰动运动方程可以看出纵向运动方程的扰动变量主要有升力系数误差阻力系数误差ΔCx、俯仰力矩系数导数偏差俯仰操纵力矩系数导数误差俯仰阻尼力矩系数误差五项。

为了方便采用卡尔曼滤波进行弹道重构，可将动力学形式的小扰动方程转化为矩阵的形式，可以得到[8-9]：

式(2)中纵向动力系数系数采用aij的符号表示，的第一个脚注i表示运动方程的序号，第二个脚注j表示运动参数偏量的顺序号[6]。由于本文研究的是扰动因素对弹道的影响，即弹箭对各固有飞行参数误差的反应，而不纠缠于飞行器对舵面偏转的影响，因此可以认为

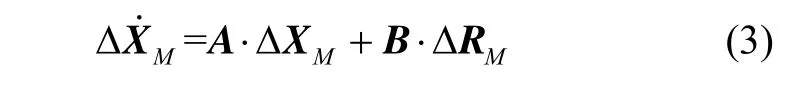
式(3)是变系数线性微分方程，采用“系数冻结法”和拉氏变换可以解得[10]：因此式(2)可表示为[5-6]：

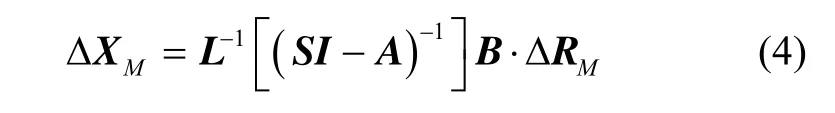
将式(4)代入式(3)得：

2 扰动源的状态建模

2.1 扰动源系统状态模型

假设扰动源服从下列方程[4-5]：

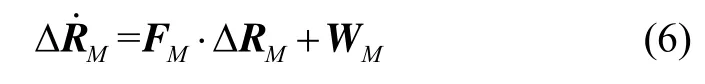
式中，FM为5× 5的矩阵，WM假设为零均值的随机白噪声。

由于气动系数RM是飞行状态XM的函数（如图1～5），它们之间的具体表达式可由实验数据拟合而来或由经验公式简化而来[6]。

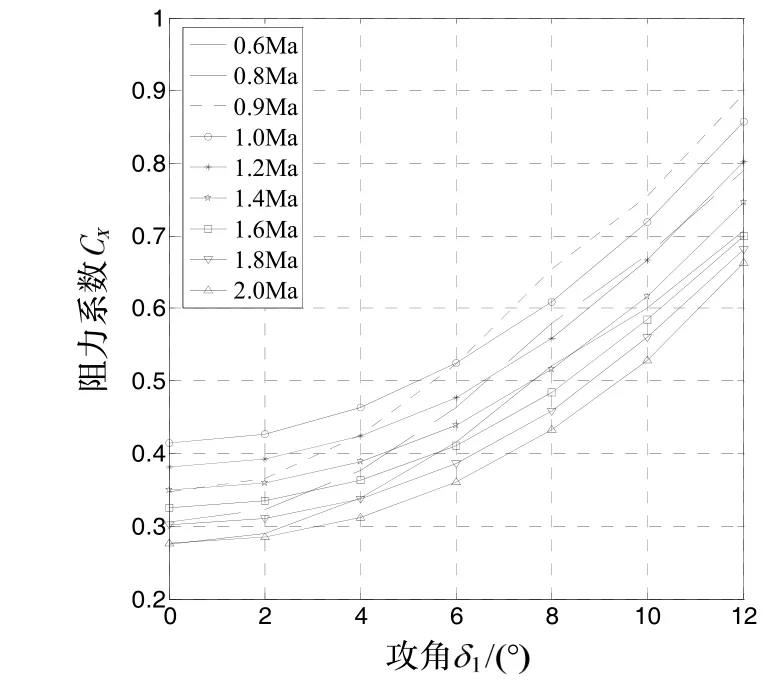
图1 阻力系数随攻角和马赫数的变化曲线Fig.1 Variation of resistance coefficient with angle of attack and Mach number

图2 随马赫数变化曲线Fig.2 Variation of with Mach number

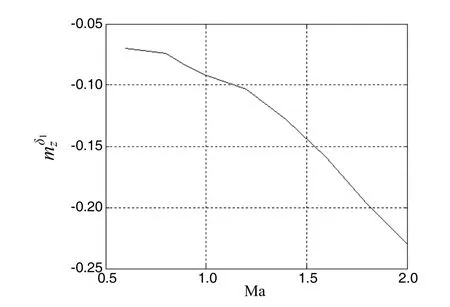
图3 随马赫数变化曲线Fig.3 Variation ofwith Mach number

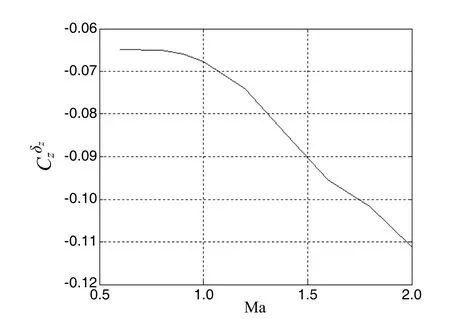
图4 随马赫数变化曲线Fig.4 Variation of with Mach number

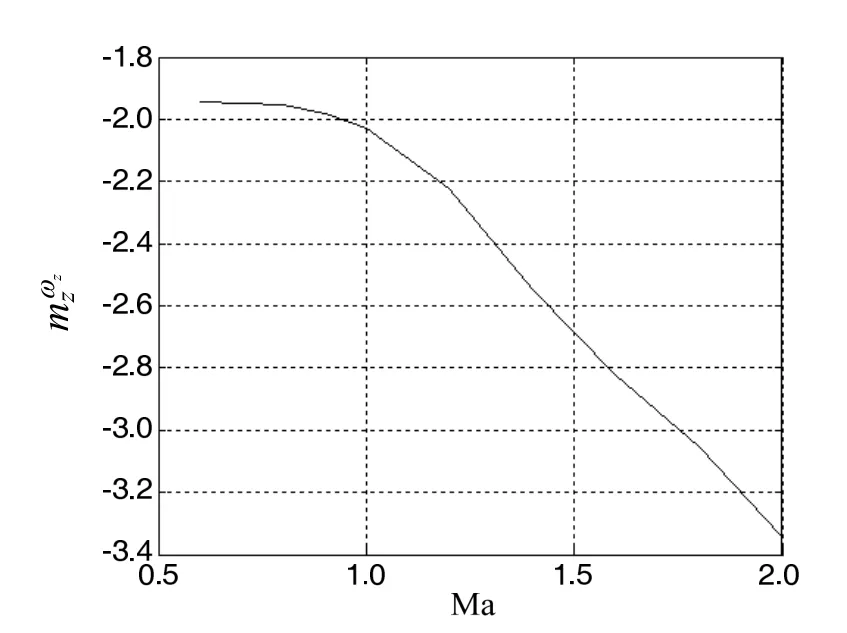
图5 随马赫数变化曲线Fig.5 Variation of with Mach number

本文根据一组给定的某弹箭气动参数数据，用数值拟合的办法得到一组被动段纵向气动参数的计算公式，然后将拟合出来的公式进行泰勒级数展开，截取一阶项得到小扰动方程，写成矩阵的形式，如下[6-7]：

将式(4)(5)代入式(7)，可得：

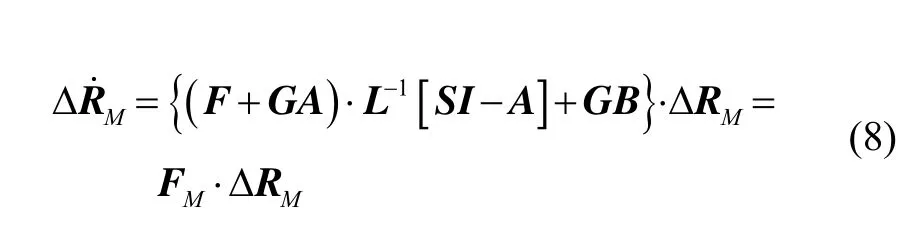
根据式(8)可以得到矩阵FM中的各元素，式(8)即为系统的状态模型。

由于采用卡尔曼滤波算法时测量值必须是系统状态参数的线性组合，因此考虑利用ΔXM与ΔR之间的关系，寻找δρ与ΔR之间的线性关系，将Δx、Δy、Δz扩充到纵向扰动方程(3)中的状态量中[9-11]，则：

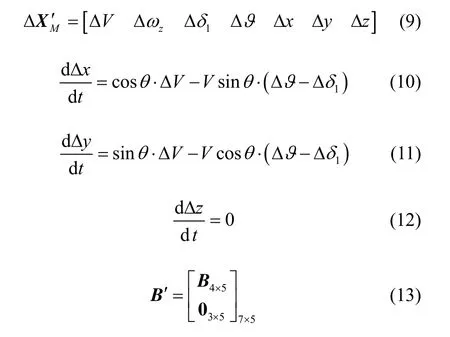
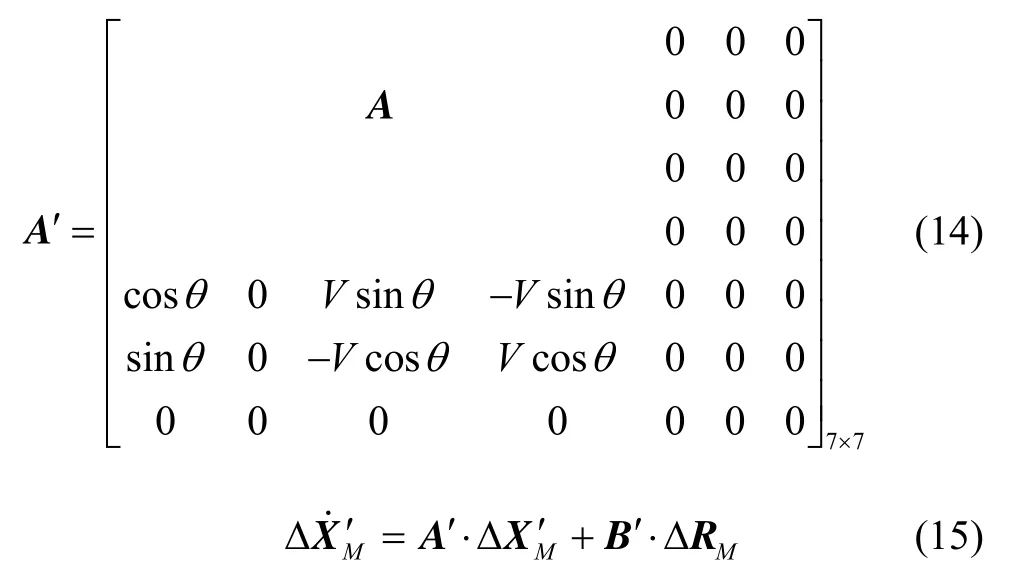
求解上述方程(15)，得：

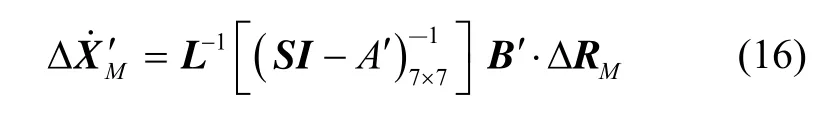
2.2 系统量测模型

三坐标雷达可以实时测定弹丸飞行时的空间三维坐标（见图6示意图）。

图6 雷达测量飞行弹丸示意图Fig.6 Sketch map of radar measuring flight projectile

设弹丸的真实位置坐标为(x,y,z)，运动方程计算出的弹丸位置为(xE,yE,zE)，三坐标雷达测量的坐标为(xL,yL,zL)，弹丸至发射原点的真实距离为r，运动方程计算的距离为Eρ，则有[12]：

相对真实位置(x,y,z)，将Eρ进行一阶泰勒展开，得：

雷达测量误差为雷达测量值与弹丸真实位置的差值，即

雷达测量的弹丸至发射点的距离为

则雷达与运动方程计算得到的距离之差为：

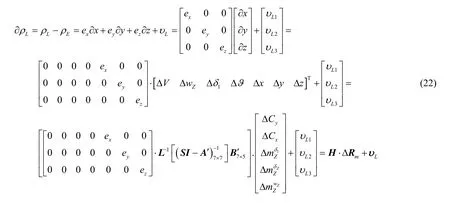
式(22)即为系统的量测模型。

3 扰动源的最优估计算法

由第2节公式(9)和(22)可知，扰动源系统的状态方程和量测方程具有如下形式：

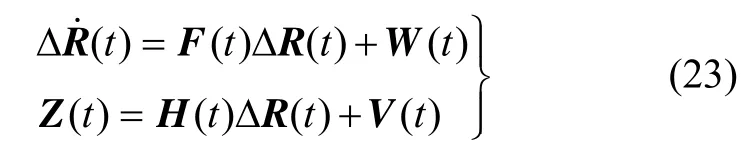
式中，W(t)、V(t)分别称为连续系统的系统噪声矩阵和量测噪声矩阵。将上述方程(23)进行离散化，可得：

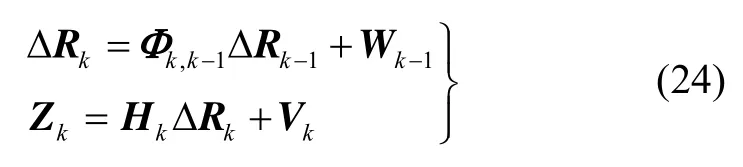
根据离散后的方程，可以设计卡尔曼滤波器，对相关状态变量进行最优估计[13]。

4 仿真计算

为进行动态仿真，需要给定火箭弹的飞行轨迹（见图7）。仿真初始条件如下：

图7 被动段纵向弹道平面Fig.7 Longitudinal trajectory plane of passive segment

采样周期为0.05 s。仿真结果如图7～12所示。

由仿真图 7～12可以看出，系统各状态的估计值精度较高，基本上在滤波开始后的20s以后，其状态估值均趋于稳定，俯仰操纵力矩系数导数误差的精度稳定在±0.007 (°)-1范围内，阻力系数误差ΔCx的精度趋于±0.025之间，升力系数误差ΔCy基本稳定在±0.12之间，俯仰力矩系数对1δ的导数偏差精度稳定在±0.011 (°)-1之间，俯仰阻尼力矩系数误差的精度基本上收敛于±0.009 (°)-1之间。由此可以看出：采用雷达测量数据对弹箭气动系数误差干扰源进行最优估计，可以得到精度较高的气动参数，进而为重构高精度的飞行外弹道状态参数创造条件。

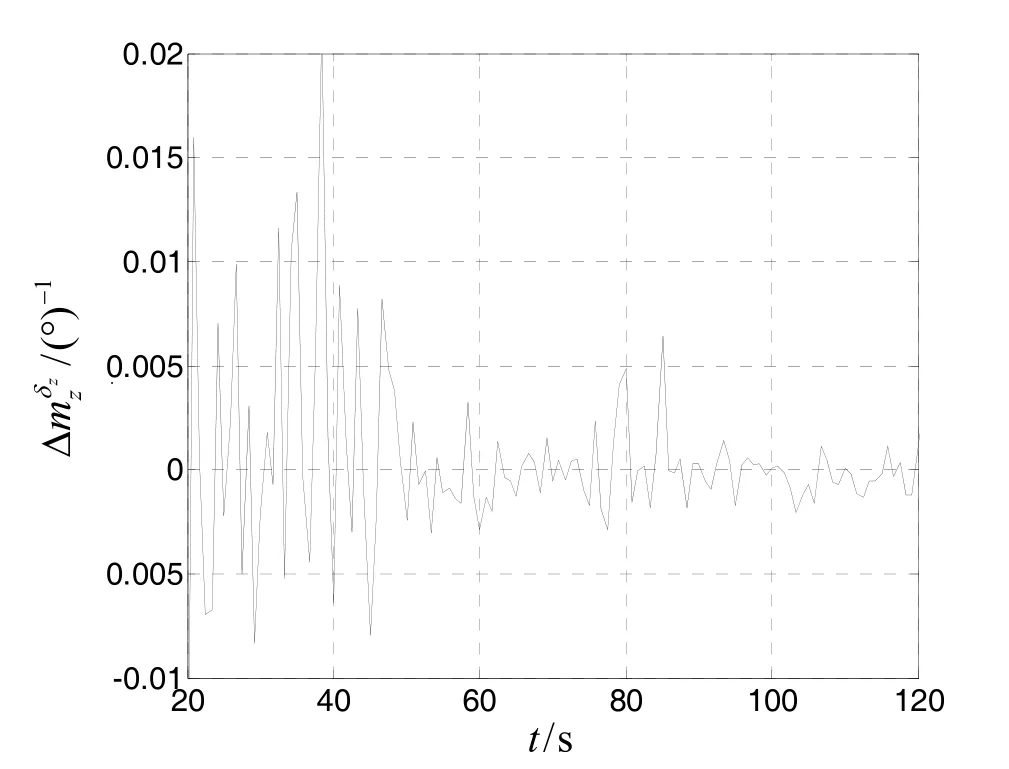
图8 的状态估值Fig.8 The state valuation of

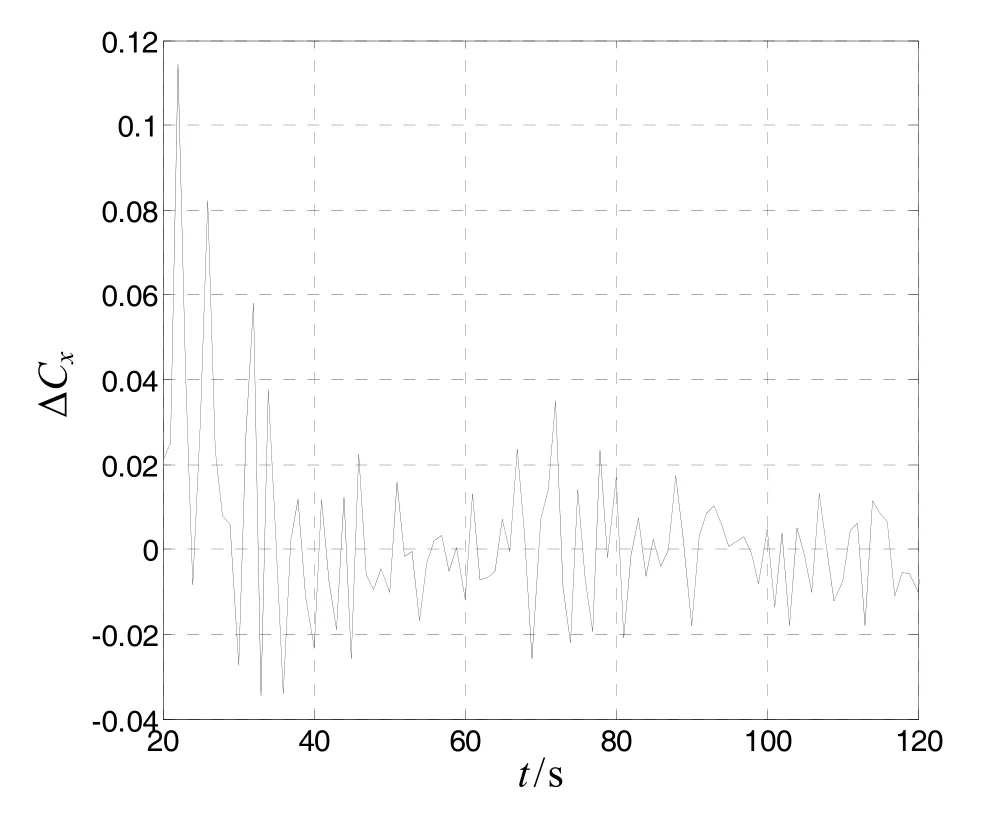
图9 ΔCx的状态估值Fig.9 The state valuation ofΔCx

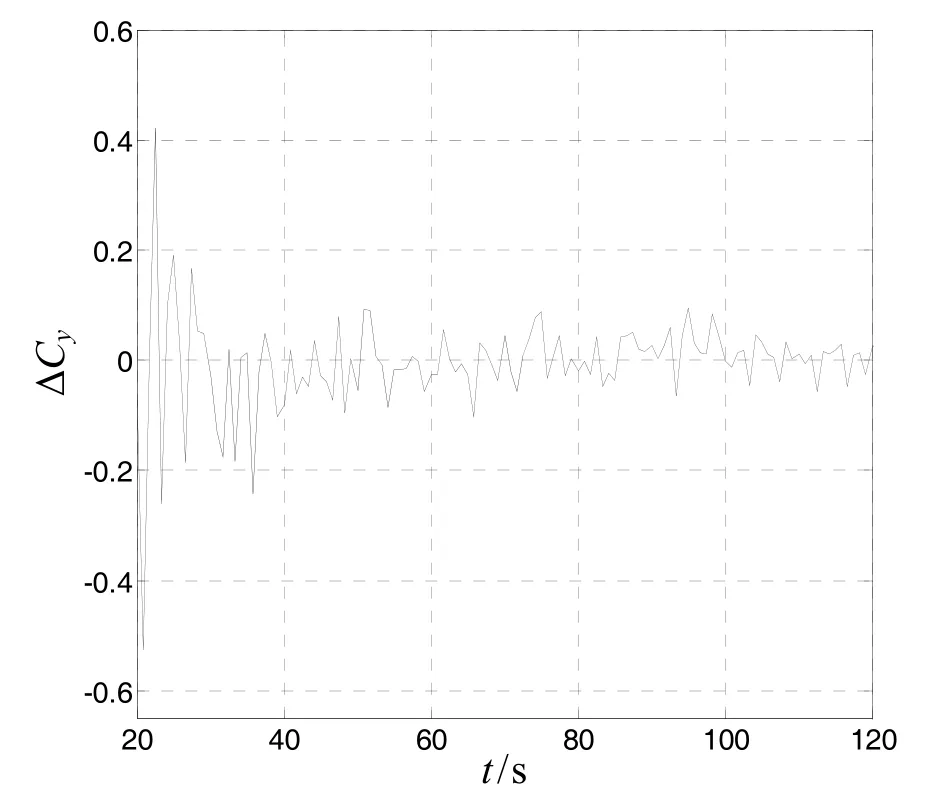
图10 ΔCy的状态估值Fig.10 The state valuation ofΔCy

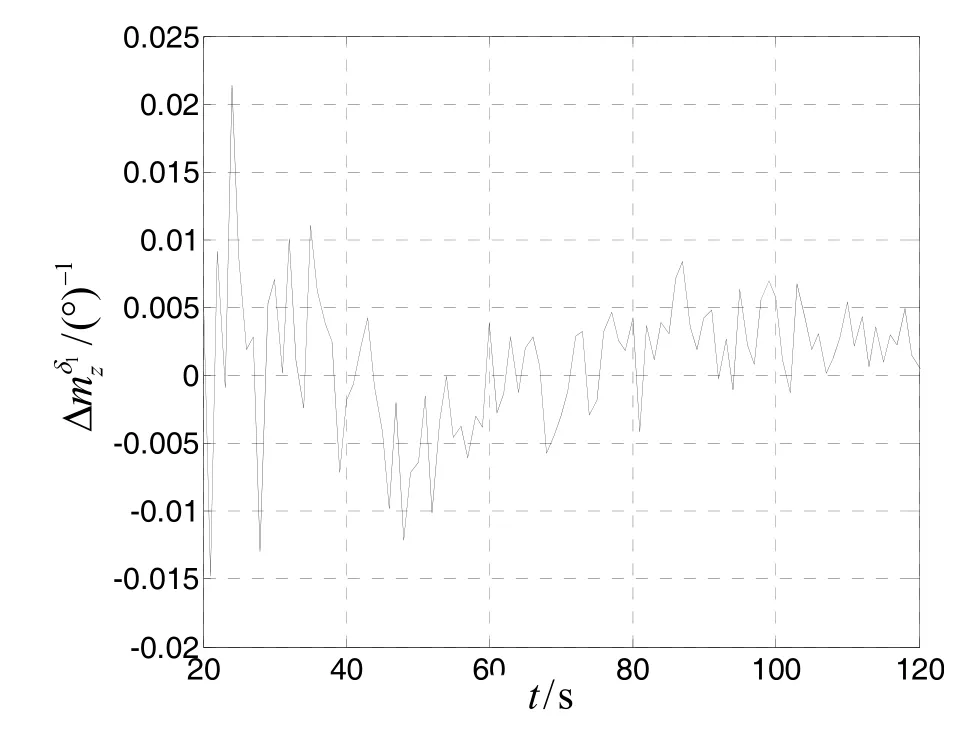
图11 的状态估值Fig.11 The state valuation of

图12 的状态估值Fig.12 The state valuation of

5 结 论

本文以弹体的纵向运动面为研究对象，推导了包含干扰源在内的纵向扰动方程，建立了以气动系数误差干扰源为状态量的系统状态模型和以雷达观测量为量测量的系统量测模型，并对模型进行仿真计算。计算结果表明：利用雷达观测量对被动段纵向平面的气动系数误差干扰源进行最优估计是有效的。该算法对提高弹箭的导航控制精度具有较大的现实意义，可为工程应用提供一定的技术参考。

（References）：

[1]Li Yong-chen, Li Jian-xun. Robust adaptive kalman filtering for target tracking with unknown observation noise[C]//Proc of 24th Chinese Control and Decision Conference. Taiyuan, 2012: 2075-2080.

[2]杨荣军, 王良明, 修观, 等. 利用雷达测量数据的实际弹道重建[J]. 弹道学报, 2011, 23(3): 43-46.Yang Rong-jun, Wang Liang-ming, Xiu Guan, et al.Trajectory reconstruction using radar measured data[J].Journal of Ballistics, 2011, 23(3): 43-46.

[3]Park D B, Shin D H, Oh S H. Development of a GPS/INS system for precision GPS guided bombs[J]. IEEE Aerospace and Electronic Systems Magazine, 2012, 27(3):31-39.

[4]Kim J, Vaddi S S, Menon P K. Comparison between nonlinear filtering techniques for spiraling ballistic missile state estimation[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(1): 313-328.

[5]Gupta K K, Voelker L S. Aeroelastic simulation of hypersonic flight vehicles[J]. AIAA Journal, 2012, 50(3):717-723.

[6]韩子鹏. 弹箭外弹道学[M]. 北京: 北京理工大学出版社, 2008.

[7]Danowsky B P, Chrstos J R, Klyde D H, et al. Evaluation of aeroelastic uncertainty analysis methods[J].Journal of Aircraft, 2010, 47(4): 1266-1273.

[8]Babbar Y, Suryakumar V S, Strganac T W. Experiments in free and forced aeroelastic response[C]//51st AIAA Aerospace Sciences Meeting. Texas, 2013.

[9]Brown R L, Das K, Whitcomb J D, et al. Aeroelastic simulation of structures in hypersonic flow[C]//Proceedings of 53rd AIAA/ASME/ASCE/AHS/ASC Structures,Structural Dynamics, and Materials Conference. Honolulu,Hawaii, USA, 2012.

[10]夏红伟, 李秋实, 李莉, 等. 基于 hp 自适应伪谱法的飞行器再入轨迹优化与制导[J]. 中国惯性技术学报,2015, 23(6): 818-823.Xia Hong-wei, Li Qiu-shi, Li Li, et al. Trajectory optimazation and guidance for reentry craft based on hp-adaptive pseudospectral method[J]. Journal of Chinese Inertial Technology, 2015, 23(6): 818-823.

[11]梁明. 靶弹动力学模型参数辨识与弹道仿真[J]. 战术导弹技术, 2012(3): 48-53.Liang Ming. Dynamic model parameter identification and trajectory simulation of target missile[J]. Tactical Missile Technology, 2012(3): 48-53.

[12]史金光, 刘猛, 曹成壮, 等. 舰船运动对弹道修正弹预报弹道落点的影响分析[J]. 南京理工大学学报, 2014,38(3): 366-374.Shi Jin-guang, Liu Meng, Cao Cheng-zhuang, et al.Effects of warship motion on predicted trajectory falling points for trajectory correction projectiles[J]. Journal of Nanjing University of Science and Technology, 2014,38(3): 366-374.

[13]周宏宇, 王小刚, 崔乃刚, 等. 基于 hp 自适应伪谱法的组合动力可重复使用运载器轨迹优化[J]. 中国惯性技术学报, 2016, 24(6): 832-837.Zhou Hong-yu, Wang Xiao-gang, Cui Nai-gang, et al.Trajectory optimization of reusable vehicle with combined power based on hp adaptive pseudospectral algorithm[J]. Journal of Chinese Inertial Technology,2016, 24(6): 832-837.

Optimal estimation of missile disturbance source based on radar measurement data

DING Chuan-bing
(China Ship Development and Design Center, Shanghai 201108, China)

In order to calculate the flight state parameters of shipborne weapons accurately, the equations of longitudinal perturbation kinematics with error disturbance source are deduced based on the longitudinal motion process of the missile. The “coefficient freezing method” and the Laplace transform are used to analyze the motion equation solution. The aerodynamic parameter formula of the longitudinal motion during passive phase is fitted out, and the measurements of the coordinate radar are used as the system measurement equation to optimally estimate the aerodynamic parameter error source. Experiment results show that: the algorithm can stabilize the error of the steering torque coefficient to within ±0.007 (°)-1, and the accuracy of the resistance coefficient tends to be within ±0.025; the lift coefficient error is basically stable to within ±0.12; the accuracy of the torque coefficient is within ±0.011 (°)-1; the accuracy of the torque coefficient of the pitching damping converges to within ±0.009 (°)-1, and the convergence speed of the algorithm is fast. The proposed algorithm can provide technical references for the reconstruction of high-precision trajectory parameters.

optimal estimation; longitudinal motion; perturbation source; radar

1005-6734(2017)04-0544-06

10.13695/j.cnki.12-1222/o3.2017.04.021

TJ413.6

A

2017-05-20；

2017-07-24

兵科院重点预研项目（20402020101）

丁传炳（1984—），男，工程师，博士，从事水面舰船作战系统总体技术研究。E-mail: sfdcb802@163.com