三相EMI滤波器宽频电路快速建模方法

郑陈达

(国网福建省电力有限公司 检修分公司，福建 福州350003)

三相EMI滤波器宽频电路快速建模方法

郑陈达

(国网福建省电力有限公司 检修分公司，福建 福州350003)

EMI滤波器的宽频模型对于滤波器的设计、产品性能的预估有重要的帮助，是电磁干扰分析预测的前提条件。目前对于该领域的研究基本停留在对单相EMI滤波器宽频建模，而对三相EMI滤波器宽频建模仍存在困难。针对上述问题文中提出将点对点阻抗模型应用于三相EMI滤波器宽频建模，通过参数测量建立了一种三相EMI滤波器的计算模型，结合时域递归卷积法计算其响应，计算结果与实测结果高度吻合。

三相EMI滤波器；点对点阻抗模型；宽频建模

各类高频电力电子设备被广泛运用于电力系统中，导致电网噪声干扰日益严重以至形成一种无形的污染。随着人们对电能质量要求的不断提高、对电力系统电磁兼容性要求愈发严格，如何减小电磁干扰对设备和电网的影响就变得尤其重要。大量研究表明，目前针对电磁噪声干扰最经济且有效的手段是电磁干扰滤波器(EMI Filter)。通过在电源侧加装EMI滤波器，可有效抑制电源侧传来的传导干扰，提高设备的抗干扰能力，使系统满足电磁兼容要求[1-2]。

建立EMI滤波器的宽频模型不仅能够帮助改进滤波器设计，并且有助于掌握接入滤波器的电路整体电磁兼容特性。现有的EMI模型大多从滤波器本身结构与组成元件出发，建立所谓的物理模型。文献[3]通过有限元法对滤波器进行了参数提取；文献[4]在宽频阻抗参数测量的基础上建立了滤波器的宽频模型；文献[5～6]以滤波器的共模扼流圈为基础提出了具有耦合电感的宽频模型；文献[7]采用福斯特网络综合法建立了共模扼流圈的电路模型。上述文章均针对单相EMI滤波器进行了建模研究，对于三相EMI滤波器而言，这些方法并不完全适用。文献[8]基于散射参数测量提出一种三相EMI滤波器建模方法，但其建模过程过于繁琐。文献[9～11]中提供了一种可行的、针对多端子设备的模型结构,即点对点阻抗模型(Node-To-Node Impedance Function，NIF)，并证明该模型能够充分反映出设备的宽频特性。本文在此基础上对三相EMI滤波器进行了测量，确定了其宽频模型的拓扑。

1 点对点阻抗模型

绝大多数的电力设备均可由频变参数(阻抗或导纳)模型来表示，因此设备宽频参数的测量对于设备建模尤为重要。对于任意一台多端设备，其宽频参数可借由不同的端子测量组合方式确定。点对点阻抗模型(NIF模型)是一种能够有效反映多端口设备端口特性的模型结构，其基本建模思想可归纳为不探究设备内部具体结构，将设备内部所有耦合体现在端子与端子间的宽频参数上，从而使模型外部端子体现出的宽频特性同实际设备达到一致。

无源设备的NIF模型可归纳出以下两方面特性：一方面，模型中只含有阻抗或导纳支路，模型内部不存在任何形式的电流源或电压源；另一方面，随着模型端子数增加，组成模型的支路数的增速远高于端子数的增速，式(1)给出了模型端子数与支路数的关系，式中m表示支路数，n表示端子数。

m=n!/(n-2)!2!=n(n-1)/2

(1)

对于1台端子数n为3的设备而言，根据上式可得其模型的支路数同样为3，具体结构如图1所示，字母A,B,C分别表示设备的3个独立端子。

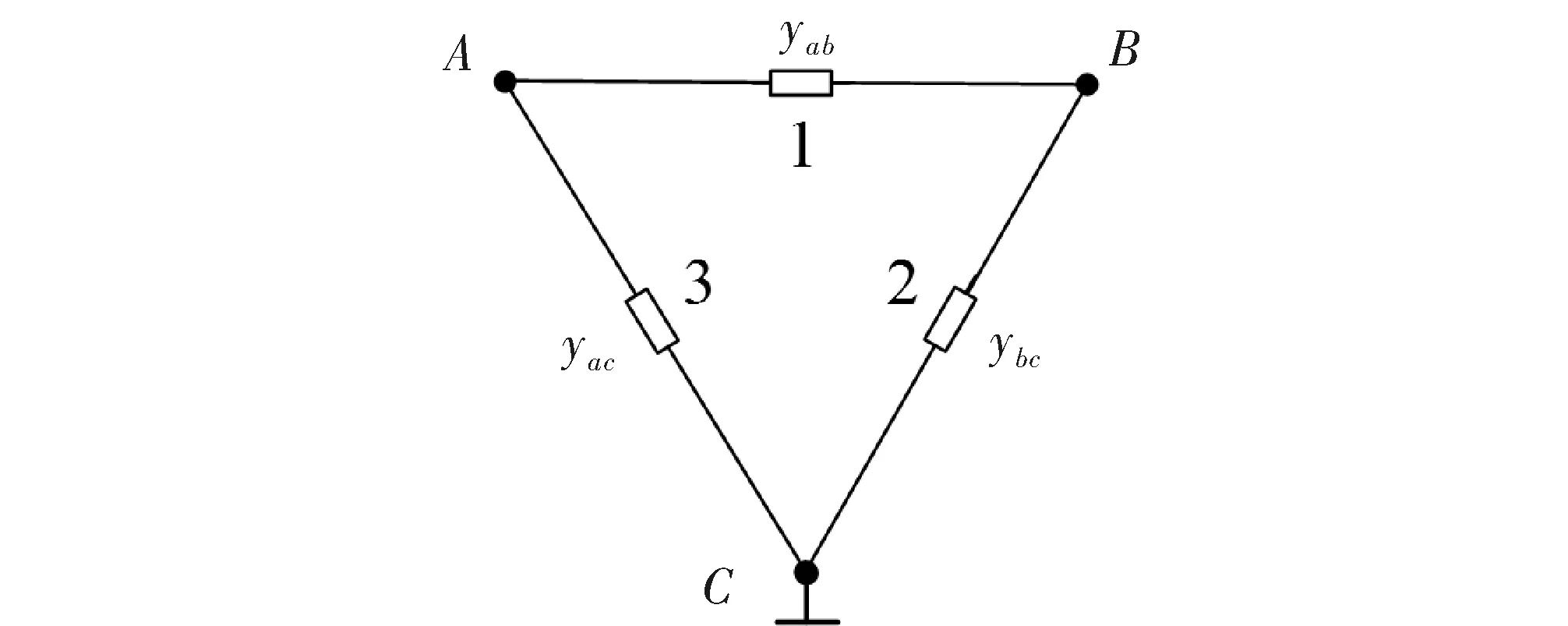
图1 三端设备相应的NIF模型示意图

如图1所示，单独求取模型各支路导纳“yab”、“ybc”、“yac”并不容易，而通过对端子的不同组合则能够间接地得到这些参数。现以端子“C”接地为例，具体做法如表1所示，共进行3组测量，组合“1”表示端子“B”接地，测量端子“A”、“C”间支路导纳；组合“2”表示端子“A”接地，测量端子“B”、“C”间支路导纳；组合“3”表示短接端子“A”、“B”，测量端子“A”、“C”间支路导纳。

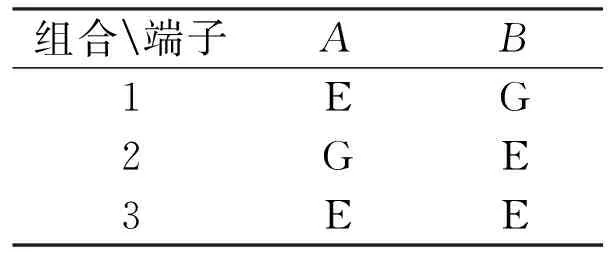
表1 对三端设备的测量组合

在表1基础上按一定规则即可形成关联矩阵C，其中矩阵C中每一列序号对应模型支路号，行序号对应表1中的组合号。具体规则如下，对于每一行元素而言，当其代表的支路任一端在表格中表示为“E”时该元素为“1”，否则为“0”；若其代表的支路两端在表1中均为“E”，则矩阵C中该元素为“0”。那么显然根据图1结合表1可得此时的关联矩阵C如式(2)所示

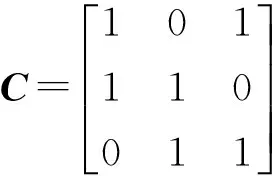
(2)

按上述测量顺序将测得的导纳参数按顺序依次排列，其结果分别设为“y1”、“y2”、“y3”，向量Yn与Yd分别如式(3)和式(4)所示。那么由式(5)和式(6)即可解得图1中模型各支路导纳参数

Yn=[yab,ybc,yac]

(3)

Yd=[y1,y2,y2]

(4)

[C][Yn]=[Yd]

(5)

[Yn]=[C]-1[Yd]

(6)

2 三相EMI滤波器宽频模型

这里以常州多极电磁环境技术公司生产的NF311A100型三相EMI电源滤波器为例，其实物如图2所示，图中的滤波器各有3个输入端及3个输出端[12-13]，根据前述的NIF模型结构可知，三相EMI滤波器的NIF模型应为如图3所示的六边形结构。对滤波器参数的测量借助Agilent4395A矢量网络分析仪，测量过程如同前述，测量的频率范围为100 kHz～30 MHz。

图2 三相EMI滤波器实物图

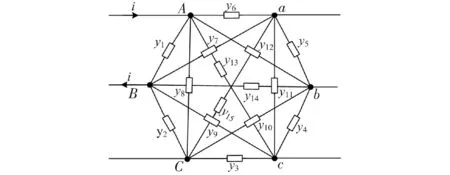
图3 三相EMI滤波器NIF模型

这里需要指出的是，关联矩阵C不是唯一的，它是根据测量时选择的不同组合方式而改变的，一般而言，测量过程中选择尽量多的端子接地能够提高测量结果的准确性。

结合前一小节介绍的方法可以快速确定滤波器NIF模型各支路导纳参数。当确定了模型中所有支路参数之后，该设备各个端口间的电压传递特性也就相应能够确定了。以图3中端口AB与bc间电压传递特性为例，假定此时在端口AB间施加任意电流源，端子A与端子B所注入电流不妨分别设为i与-i。节点C为参考点，此时的注入电流向量及节点电压向量符合式(7)～式(9)，其中矩阵Y表示以节点C为参考点时模型的节点导纳阵；U以及I分别表示此时的节点电压向量、节点电流向量

I=[i-i0 0 0]T

(7)

YU=I

(8)

U=Y

(9)

Y-1是矩阵Y的逆矩阵，若将其以式(10)中的符号矩阵形式表示，那么节点电压向量U可表示为式(11)所示

(10)

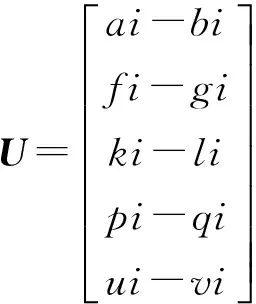
(11)

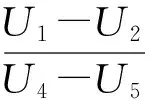
(12)

端口AB与端口bc间以符号表示的电压传递参数H见式(12)。从中不难看出电压传递参数实际上只和模型自身参数有关，与输入激励情况无关[14]。

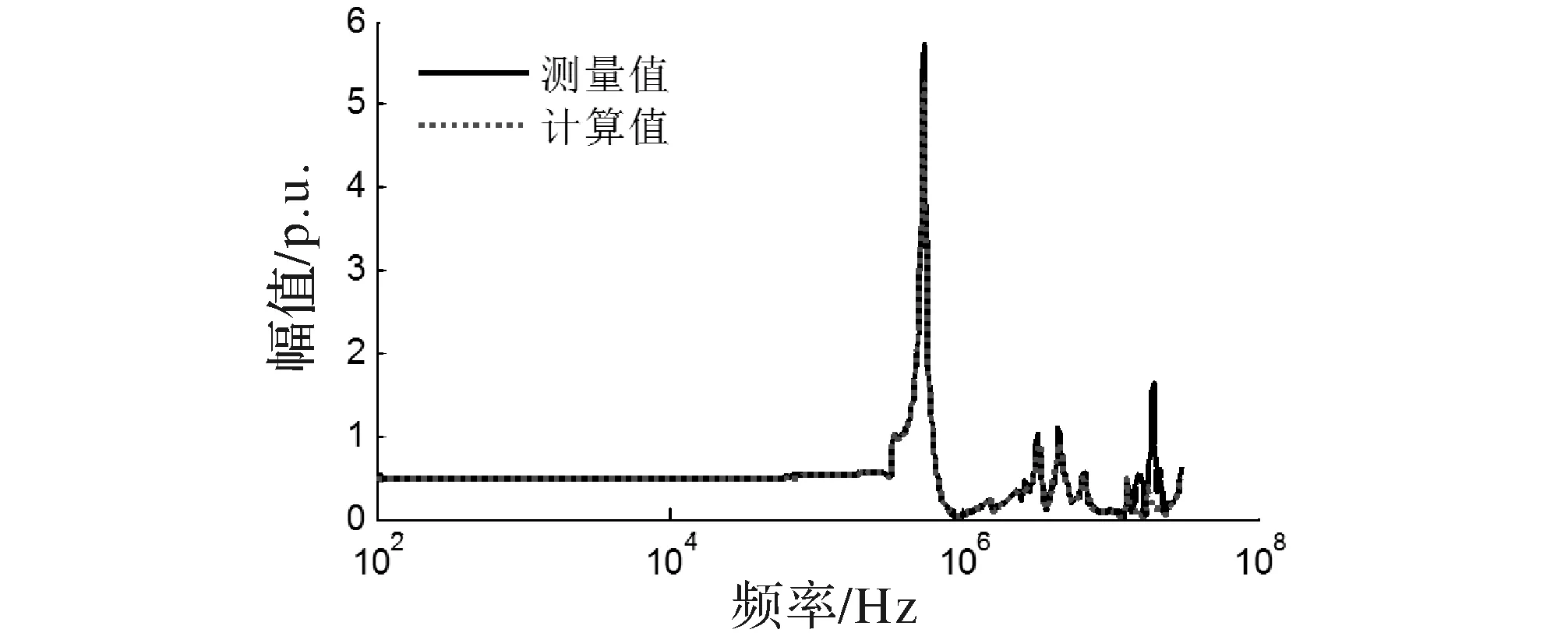
图4 AB-ab端口电压传递函数对比(C相开路)

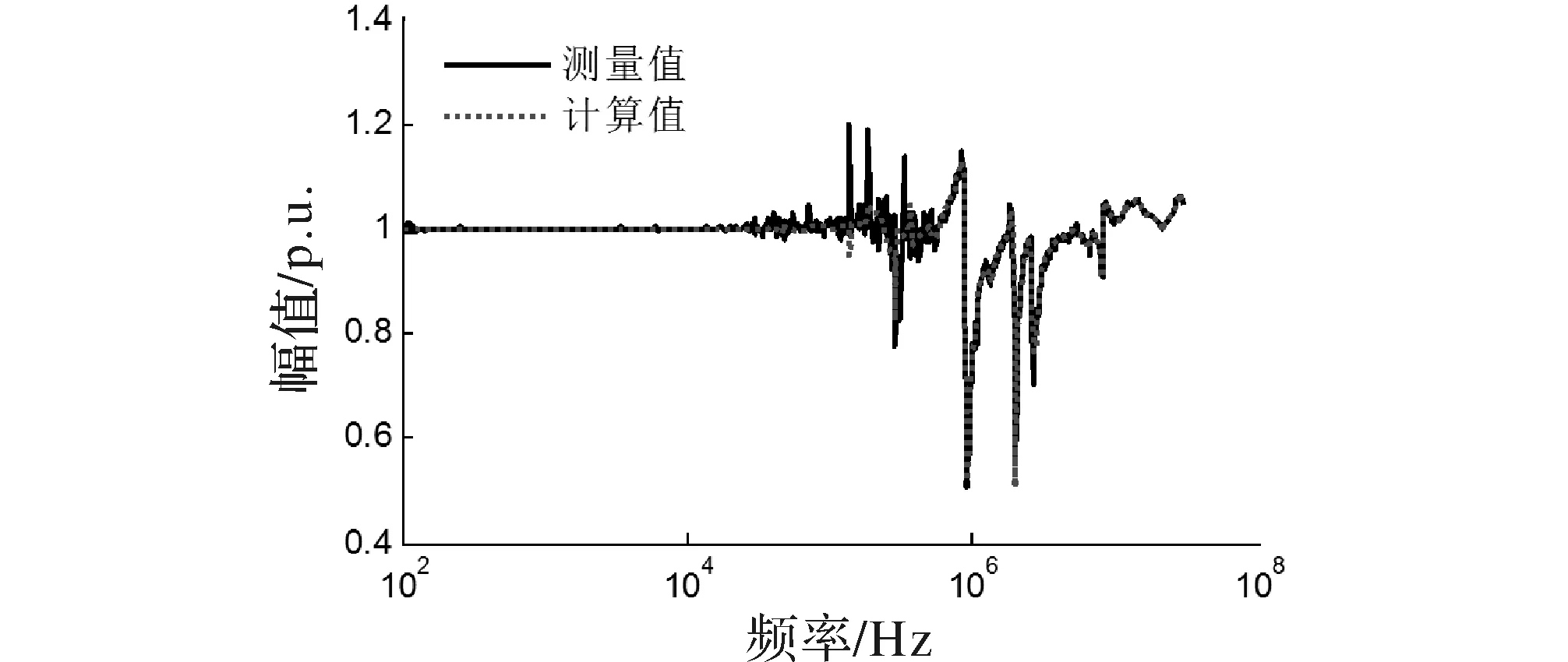
图5 AB-ab端口电压传递函数对比(C相短路)

图4和图5所示分别为三相滤波器在C相开路、短接两种情况下一次侧端口AB与二次侧端口ab之间电压传递参数测量值与计算值的对比，由对比结果可得所建立的三相EMI滤波器NIF模型准确度很高。

3 模型验证

由前述可知，此时通过模型得到的是频域上离散形式的参数，若要进行后续的电压响应计算则需要将离散形式的参数拟合成为连续函数形式。这里选用矢量匹配法(Vector Fitting,VF)进行参数拟合，再经由时域递归卷积法计算电压响应[14-15]。

将三相滤波器C相短接，在滤波器一次侧A、B相间施加陡波信号，测量此时二次侧a、b相间的响应。结果如图6所示，通过模型计算得到的响应曲线变化趋势整体上同测量曲线相符合，仅在波峰或波谷处存在偏差，总体而言这样的偏差是可以接受的。

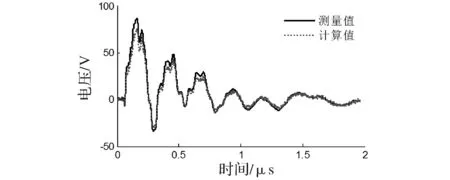
图6 电压响应对比

4 结束语

传统上关于电力系统的等值模型通常不需要考虑到宽频特性，而电力系统的日益复杂化、精密化，系统中各类干扰的增多使得设备的宽频模型变得愈发重要。本文提出的三相EMI滤波器宽频模型是对于传统模型很好的补充，该模型具有相当的精度且易于得到，在工程上具有一定实用价值。

[1] 沙占友. EMI滤波器的设计原理[J].电子技术应用,2001,27(5):46-48.

[2] 张娜,张团善,武玉婷. EMI电源滤波器的原理与分析[J]. 变频器世界,2010(12):118-119.

[3] 王世山,朱叶,沈湛.构成平面EMI滤波器元件电磁参数的提取[J].中国电机工程学报,2012,32(21):146-152.

[4] 陈恒林,陈玮,冯利民,等.基于阻抗测量的共模扼流圈高频建模[J]. 电工技术学报,2007,22(4):8-12.

[5] Kotny J L,Margueron X,Idir N. High frequency modeling method of EMI filters[C].Japan:Energy Conversion Congress and Exposition,IEEE,2009.

[6] KotnyJ L,Margueron X,Idir N.High-frequency model of the coupled inductors used in EMI filters[J]. IEEE Transactions on Power Electronics,2012,27(6):2805 - 2812.

[7] 陈恒林,钱照明. 用于电磁干扰分析的共模扼流圈高频模型[J]. 浙江大学学报：工学版,2007,41(11):1845-1849.

[8] Wei J,Gerling D,Galek M. S-parameters characterization and sequence model of three-phase EMI filter[C]MA,USA:Industrial Electronics Society,IECON 2013 - 39th Annual Conference of the IEEE,IEEE,2013.

[9] Liu Y，Sebo S A，Caldecott R，et al.Modeling of converter transformers using frequency domain terminal impedance measurements[J]．IEEE Transactions on Power Delivery,1993,8(1):66-72.

[10] Caldecott R，Liu Y，Sebo S A，et al.Measurement of the frequency dependent impedance of major station equipment[J].IEEE Transactions on Power Delivery,1990,5(1):474-480.

[11] Liu Y,Sebo S A,Caldecott R,et al.Power transformer resonance-measurements and prediction[J]．IEEE Transactions on Power Delivery,1992,7(1):245-253.

[12] 羊绍林,张庆重,奚望,等. 基于LTCC的小型化中频带通滤波器设计[J].电子科技,2016,29(4):147-149.

[13] 胡旭,李刚. 基于模型校正技术的滤波器设计方法[J].电子科技,2016,29(2):119-121.

[14] 王智慧,张重远.数值拉普拉斯反变换和时域递归卷积算法分析与比较[C].北京：中国高等学校电力系统及其自动化专业学术年会,2011.

[15] 张玉强,葛德彪. 基于半解析递归卷积的通用色散介质FDTD方法[J].物理学报,2009,58(7):4573-4578.

Research on Fast Modeling of Three-phase EMI Filter Broadband Model Based on Node-to-node Impedance Function

ZHENG Chenda

(Maintenance Branch of Fujian Electric Power Co.,Ltd.,Fuzhou 350003,China)

The broadband modeling of three phase EMI filter is of great help for the design of the filter and the prediction of the performance of the product. It is the precondition for the analysis and forecast of electromagnetic interference. At present,the research in this field focus on the single-phase EMI filter broadband modeling while it is still difficult to model a three-phase EMI filter.Nod-to-nod impedance function is applied to three-phase EMI broadband filter modeling,The calculation model of a three-phase EMI filter is established by parameter measurement,and the response is calculated by using the recursive convolution method in time domain. The calculated results are in good agreement with the measured results.

three-phase EMI filter;NIF;broadband model

TN713

A

1007-7820(2017)11-060-04

2016- 12- 19

郑陈达 (1989-),男,硕士,工程师。研究方向：电工理论及新技术。

10.16180/j.cnki.issn1007-7820.2017.11.017