一元立木材积表的适用精度检验方法探讨
杜德鱼
(1.西安外事学院,西安 710077;2.西北农林科技大学,陕西 杨凌 712100)
一元立木材积表的适用精度检验方法探讨
杜德鱼
(1.西安外事学院,西安 710077;2.西北农林科技大学,陕西 杨凌 712100)
国家森林资源连续清查中长期使用的一元立木材积表,其适用精度如何,一直是值得关注的问题。以第九次全国森林资源清查2014年陕西省的栎类(Quercusspp.)样地调查数据为基础,对其采用的4个栎类一元材积表的适用精度检验方法进行探讨。利用栎类样地的466组平均胸径和平均树高数据,以及全部平均高测定样木的1 447组胸径和树高成对数据,按2套方案分别建立4个栎类的新的树高曲线,从而形成4个新的一元材积表,并与原来的材积表进行对比,计算总体相对误差。结果表明:原一元材积表有2个的估计误差在±3%以内,另外2个的估计误差超出了±5%,误差最大的达到了-10%左右。因此,长期使用固定不变的一元材积表可能会导致材积估计结果出现偏差,建议每10年或20年对一元立木材积表(模型)进行适用精度检验,对偏差过大的一元材积表应该及时予以修正。
材积估计;一元材积表;相对误差;栎类;陕西
0 引言
林业数表是森林资源经营管理的重要计量工具,是森林资源调查监测与评价工作的度量衡[1]。在林业数表中,立木材积表是最重要的基础计量数表[2]。20世纪70年代末,我国就组织编制了56个二元立木材积表,并以行业标准颁布实施[3]。随后,全国各省以二元材积表为基础导算了一元材积表[4],并在国家森林资源连续清查中得到了广泛应用[5]。关于长期使用一元材积表可能存在偏差的问题,尽管已有学者[5-7]开展过一些研究,但还没能引起足够重视。由于从国家森林资源连续清查体系建立至今,各省在材积估计时,一直还是采用初查时导算出的一元材积表[5],目前其适用精度如何,尚未有明确结论。为了探讨一元立木材积表适用精度的检验方法,本文将利用第九次全国森林资源清查2014年陕西省的栎类(Quercusspp.)样地调查数据,通过建立新的树高曲线模型和构建新的一元立木材积表,计算陕西省的4个栎类一元材积表的相对误差,分析其适用性,以期为今后改进一元立木材积估计方法提供依据。
1 数据与方法
1.1数据资料
本文所用数据是国家森林资源连续清查固定样地调查数据,来自第九次全国森林资源清查2014年陕西省清查项目。选择了优势树种为栎类的林分和疏林样地466个,数据资料包括样地因子表、样木因子表和平均木树高测定记录表。陕西省共有一元立木材积表24个,其中栎类有4个(材积式代码分别为2,9,15,20号),本文分别用1,2,3,4来区分。1号材积表用于咸阳、延安、铜川和韩城4市,2号材积表用于西安、宝鸡和汉中3市,3号材积表用于渭南、商洛2市,4号材积表用于安康市。对应于栎类4个立木材积表,表1列出了各自的样地数量及其样地的平均胸径和平均树高、平均木的胸径和树高,以及样地全部活立木的胸径分布范围。

表1 栎类样地数据的胸径和树高分布范围
注:平均木和全部样木未包括栎类以外的其它树种。
1.2分析方法
1.2.1老一元材积公式的拟合
考虑到陕西省栎类的4个一元材积表均无材积计算公式,参照有关文献[8-9]先建立一元立木材积模型,具体步骤如下:
1)根据各个一元立木材积表和部颁西北地区栎类的二元立木材积模型[3]((1)式)导算出每个径阶D所对应的树高H,然后拟合基于Richards函数的树高曲线模型((2)式)。
V=0.000060971D1.8735H0.94158
(1)
H=a[1-exp(-bD)]c
(2)
(2)式中:a,b,c为参数;exp表示以自然数e为底的指数函数。
2)将(2)式代入(1)式,就得到对应于一元材积表的材积模型(老一元材积公式)。利用一元材积表中的胸径和材积成对数据,可以计算拟合的老一元材积公式的相关统计指标,如相关指数或确定系数(R2)、平均预估误差(MPE)、总体相对误差(TRE)和平均系统误差(ASE)等,计算公式如参考文献[10]中所述。
1.2.2新一元材积公式的建立
本文尝试利用2组数据建立新的一元材积公式。第1组是466对林分平均胸径和树高数据,第2组是1 447对平均木的胸径和树高数据。利用这2组数据先建立树高曲线模型,除了(2)式以外,还同时建立了如(3)式、(4)式所示的幂函数和抛物线模型。
H=aDb
(3)
H=a+bD+cD2
(4)
式中:a,b,c为参数;D,H分别为胸径和树高。通过模型相关指数和外推性能等进行综合对比,从中选定拟合效果较好、适应性更广的树高曲线模型,代入(1)式即得到新的一元材积公式。
1.2.3材积估计相对误差的计算
利用表1中提到的全部样木,分别按新、老一元材积公式计算4个材积表的材积估计值,然后以新的一元材积公式估计值为基础,计算老材积公式的总体相对误差((5)式)。
TRE=(V老-V新)/V新×100%
(5)
式中:V新,V老分别指新、老材积公式计算的样木材积总和。按照相关技术规定[11],立木材积表的估计误差应该在±3%以内。如果按(5)式计算的总体相对误差超出±3%的范围,则表明该材积式已经存在明显的偏差,需要予以修正或更新。
2 结果与分析
按照前述方法,对陕西省栎类4个一元立木材积表先进行数式化,得到其相应的树高曲线模型,然后代入(1)式得出一元材积公式。经过检验,材积公式与材积表之间的相关指数都在0.999 5以上,总体相对误差(TRE)均在±0.1%以内,平均预估误差(MPE)和平均系统误差(ASE)基本都在0.5%以内,说明数式化以后的材积公式与原材积表几乎是等同的,既为全部样木的材积计算奠定了基础,也为今后一元材积表的应用提供了方便。表2为栎类一元立木材积公式的参数值及相关统计指标。
利用第1组466对林分平均胸径和平均树高数据及第2组1 447对平均木的胸径和树高数据,分别建立树高曲线模型(以下分别称为方案A和方案B)。从Richards函数、幂函数和抛物线3种模型的拟合结果可知,Richards函数的拟合效果较好,且具有良好的外推性能,因此最终选用Richards函数的树高曲线模型,其模型参数值及相关指数如表3所示。从相关指数看,材积表1和4是方案A所建树高曲线拟合效果较好,而材积表2和3是方案B所建树高曲线拟合效果较好;从模型参数的稳定性看,则方案B要好一些。图1展示了两套方案建立的4个新材积表所对应的树高曲线。

表2 栎类一元立木材积公式的参数值和统计指标

表3 栎类树高曲线模型的参数值和相关指数

图1 A和B两套方案的树高曲线对比
利用方案A和方案B所建树高曲线模型代入(1)式,可以分别得到4个栎类材积表对应的两套新的一元立木材积公式。然后分别利用新老材积公式计算全部21 690株样木的材积估计值,并按(5)式计算基于两套新材积式的总体相对误差,其结果如表4所示。

表4 栎类原一元材积表的总体相对误差
从表4可以看出,与新建一元材积公式的估计结果相比,栎类4个老一元材积公式的总体相对误差,只有2个在±3%以内,另外2个的估计误差超出了±5%,误差最大的达到了-10%左右。这一结果表明,4个栎类一元材积表有2个已经超出了允许误差范围,应该予以修正或更新。图2显示了相差最大的材积表3的新、老树高曲线对比情况。
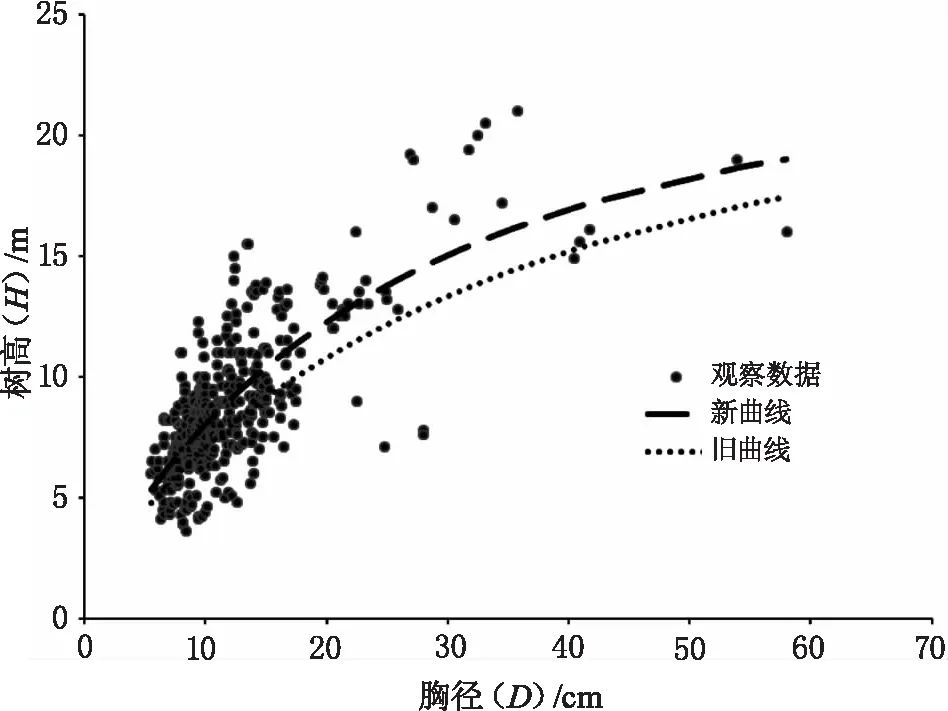
图2 材积表3新老树高曲线对比
3 结论与讨论
本文以第九次全国森林资源清查2014年陕西省的466个栎类固定样地调查数据为基础,对其采用的4个栎类一元材积表的适用精度检验方法进行了探讨,可以得出以下结论。
1) 基于林分平均胸径和平均树高数据与基于平均木胸径和树高数据两套方案,都能有效检验一元立木材积表的适用精度;综合考虑模型相关指数和参数稳定性,基于平均木胸径和树高数据的检验方案B要更好一些。
2) 陕西省4个栎类的一元立木材积表,有2个的估计误差已经超出了±3%的允许范围;为了保证材积估计值无偏,有必要重新编制适用的一元材积表。
目前各省在森林资源连续清查中使用的一元立木材积表,还是清查体系初建时根据部颁二元立木材积表导算的。长期使用固定不变的一元材积表,可能会导致材积估计结果出现偏差。建议各省参照本文提出的方法,对现行的一元立木材积表(模型)进行一次适用精度检验。对偏差过大的一元材积表应该及时予以修正,或者按照原来的方法导算新的一元立木材积表。以后每隔10年或20年,也需对一元材积表进行定期检验,以确保材积估计结果的无偏。
志谢:
本文所用基础材料由国家林业局西北林业调查规划设计院侯晓巍高级工程师提供,特此致谢!
[1] 白卫国,王祝雄.论我国林业数表体系建设[J].林业资源管理,2009(1):1-7.
[2] 曾伟生.全国林业数表体系框架初探[J].中南林业调查规划,2009,28(4):1-4.
[3] 中华人民共和国农林部.立木材积表(LY 208-77)[S].北京:中国标准出版社,1977.
[4] 常昆.导算一元立木材积表的技术方法[J].林业调查规划,1977(1):1-10.
[5] 曾伟生.国家森林资源连续清查中的材积估计问题探讨[J].中南林业调查规划,2007,26(2):1-3.
[6] 辛文荣,林建方,张海凤.关于青海省立木一元材积表的使用问题[J].青海农林科技,1996(4):45-47.
[7] 向建华.我区现有一二元立木材积表应用偏差问题的探讨[J].中南林业调查规划,1996,15(1):8-10.
[8] 曾伟生.论一元立木材积模型的研建方法[J].林业资源管理,2004(1):21-23.
[9] 魏建祥,曾伟生.论北京市一元立木材积表的数式化方法[J].林业资源管理,2009(6):44-45.
[10] 曾伟生,唐守正.立木生物量模型的优度评价和精度分析[J].林业科学,2011,47(11):106-113.
[11] 中华人民共和国林业部.林业专业调查主要技术规定[M].北京:中国林业出版社,1990.
DiscussiononTestMethodforApplicationAccuracyofOne-variableTreeVolumeTables
DU Deyu
(1.Xi′anInternationalUniversity,Xi′an710077,China;2.NorthwestAgricultureandForestryUniversity,Yangling,Shaanxi712100,China)
Applicable accuracy of one-variable tree volume tables used in national continuous forest inventory(NFI)for long-term perspective has been worthy of attention.Based on the mensuration data of sample plots from oak(Quercusspp.)forests in 2014 Shaanxi of the 9th NFI,the test method for applicable accuracy of 4 one-variable tree volume tables was discussed.The approach is to develop 4 tree height-diameter regression models for oak forests using two sets of data,466 pairs of mean diameter and mean tree height of oak stands and 1447 pairs of diameter and tree height of average oak trees,and obtain 4 new one-variable tree volume tables,then compare with the old tables and calculate total relative errors(TRE).The results showed that the TREs of 2 old one-variable tree volume tables did not exceed ±3%,and the TREs of other 2 volume tables exceeded ±5%,and the largest one reached about -10%.Therefore,keeping the one-variable tree volume tables constant in long-term application may cause bias in volume estimation.It is recommended that one-variable tree volume tables/models need to be tested every 10 or 20 years,and the significantly biased ones should be corrected in time.
volume estimation,one-variable volume table,relative error,Quercusspp.,Shannxi
S758.62
A
1002-6622(2017)05-0035-04
10.13466/j.cnki.lyzygl.2017.05.007
2017-09-04;
2017-09-27
杜德鱼(1950-),男,陕西华县人,教授,研究方向:林业调查、林业生态和社会政策等。
Email:19703631@qq.com

