基于MED和VMD的风电机组发电机滚动轴承故障特征提取方法

张 伟， 赵洪山

(华北电力大学 电气与电子工程学院，河北 保定 071003)

●能源及动力工程●

基于MED和VMD的风电机组发电机滚动轴承故障特征提取方法

张 伟， 赵洪山

(华北电力大学 电气与电子工程学院，河北 保定 071003)

风电机组发电机滚动轴承早期故障时，其机械振动信号包含复杂的信息成分，影响微弱故障信号的提取，导致故障识别非常困难。提出一种基于最小熵反褶积(Minimum Entropy Deconvolution，MED)和变分模态分解(Variational Mode Decomposition，VMD)结合的风电机组发电机滚动轴承故障特征提取方法。先应用MED算法对采集的振动信号进行降噪，突出被噪声所掩盖的故障冲击脉冲，后应用VMD算法对降噪后的信号进行分解，得到一系列固有模态函数(Intrinsic Mode Function，IMF)，应用峭度和相关性最大准则选取包含故障信息量最多的分量，即敏感模态分量，最后对敏感分量进行包络谱分析，提取故障特征频率。实验分析和工程案例分析结果表明，该方法可有效提取故障特征。

风电机组发电机；滚动轴承；最小熵解卷积；变分模态分解；特征提取

风力发电作为一种新型清洁可再生的能源，近年来发展迅速，然而，随着风电的大规模发展，风电机组的故障问题也愈加突出[1-3]。轴承作为风电机组的重要部件，工作条件比较恶劣，尤其是发电机滚动轴承，转速高，需要承受较大的径向载荷，极易受到损伤而引发各种故障，影响整个风机运行的稳定性。因此，为能够及时发现轴承故障，避免风电机组发生严重事故，降低维修费用，增强机组的运行可靠性，需对风电机组发电机滚动轴承早期故障特征提取方法进行研究。

滚动轴承的振动冲击信号具有周期、非平稳特性，要从振动信号中提取出反映轴承运行状态的故障特征，常用的方法包括时域法、频域法以及时频域法等。其中，基于EMD等时域分析方法得到了广泛的应用，文献[4]验证了基于EMD的轴承故障特征提取和诊断方法优于传统的包络解调方法。文献[5]将最大峭度解卷积与EMD结合提取了主轴承的故障特征，并对轴承进行了故障诊断。文献[6]提出一种基于集成经验模态分解(Ensemble Empirical Mode Decomposition，EEMD)和峭度准则的故障特征提取方法，一定程度上抑制了EMD存在的模态混叠现象。文献[7]提出一种局域均值分解(Local Mean Decomposition，LMD)与多尺度熵结合的方法，成功提取了滚动轴承故障特征信息。然而，EMD、EEMD和LMD等算法仍属于递归模态分解，存在模态混叠和端点效应，影响信号分解的准确率。

变分模态分解[8]是近几年提出的一种新的信号分解方法，能够将信号分解问题转化为完全非递归、变分模态分解问题，收敛速度快，具有良好的噪声鲁棒性和采样效应，能够较好的分离出振动数据的局部故障特征[9]。文献[10]将变分模态分解应用于滚动轴承故障诊断，并提出基于包络谱特征因子的影响参数自动搜寻策略。文献[11]提出VMD和奇异值能量差分谱结合的滚动轴承故障特征提取方法，应用奇异值能量差分谱找出敏感分量的能量突变点，再进行信息重构提取故障特征。文献[12]提出一种基于VMD和Teager能量算子结合的方法，应用Teager能量算子解调增强敏感模态分量中的故障冲击成分，成功提取了轴承故障特征。

工程实际中，轴承故障特征受噪声等干扰严重，不易被提取。最小熵反褶积通过设计滤波器能够有效抑制噪声，凸显信号中的尖锐脉冲[13-15]。因此，结合最小熵反褶积算法，提出基于MED和VMD的滚动轴承故障特征提取方法，先应用MED算法抑制噪声干扰，突出故障冲击特性，再对降噪后的解卷积信号进行VMD分解，选取包含故障信息较多的敏感模态分量，并计算其包络谱，最后对故障特征信息进行提取。

1 MED原理

最小熵反褶积基本原理是通过解反褶积突出尖脉冲，并以峭度值最大作为迭代终止条件。此算法能够突出冲击脉冲，非常适用于旋转机械冲击性故障的降噪处理。假设滚动轴承故障时，传感器采集到的离散信号为y(n)：

y(n)=h(n)·x(n)+e(n)

(1)

式中:x(n)为输入的滚动轴承冲击序列;h(n)为x(n)经过周围环境以及路径传输衰减后的响应;e(n)为噪声。为分析简便，此处忽略e(n)的影响。x(n)经h(n)作用后，y(n)中反映故障特征的冲击序列被掩盖，信息更加混乱，导致熵变大。

MED算法的本质是寻找1个逆滤波器w(n)，使得输出信号y(n)通过w(n)后尽可能的恢复x(n)的冲击特征，即

(2)

(3)

式中:x(i)为序列x(n)的第i个值。

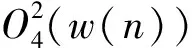
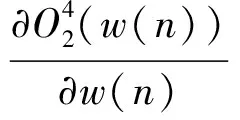
(4)

对式(2)两边同时求导得，

(5)

联合(2)、(3)、(4)、(5)式得，

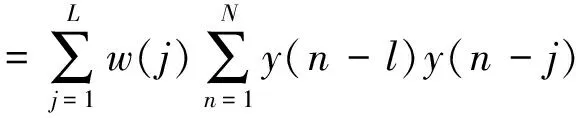
(6)

将式(6)写成矩阵形式如下，

b=Aw

(7)

式中:A为y(n)的L×L阶自相关矩阵。

b=(b(l))T，b(l)表达式为:

(8)

经迭代得逆滤波器矩阵为:

w=A-1b

(9)

最小熵反褶积的具体迭代步骤如下：

1) 初始化w(0)中所有元素为1；

2) 迭代计算x(n)=w(n)i-1·y(n)；

3) 应用式(8)计算b(l)；

4) 迭代计算w(n)i=A-1b(i)；

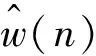
2 VMD原理

变分模态分解原理是把信号的分解过程转化为变分问题的处理，通过迭代搜寻变分模型的最优解来获取不同模态分量的频率中心和带宽，并由此实现信号频域和各个分量的自适应划分。

VMD模型变分问题的构造和求解涉及3个重要概念：经典维纳滤波、Hilbert变换和频率混合。假定将原始信号f分解为K个模态分量uk，在建模过程中，首先，通过Hilbert变换对每个uk进行解调，得到各分量的解析信号并计算其单边频谱;然后，对解析信号预估1个中心频率e-jwk t，并将每个分量的频谱调制到基频带上;最后，计算该调制信号梯度的平方L2范数，估计各模态信号的带宽。

上述VMD方法对应的约束变分模型为：

式中:{uk}={u1,…,uk}代表分解得到的k个IMF分量;{ωk}={ω1,…,ωk}表示各分量的中心频率;δ(t)为脉冲函数。

为解上述变分问题，需要引入二次惩罚因子α和Lagrange算子λ(t)，将约束性变分问题变为非约束性变分问题，变换后的增广Lagrange表达式为：

L({uk},{ωk},λ)=

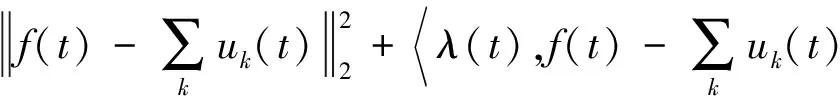
(12)

(13)

VMD分解的具体步骤如下：

2)根据(12)、 (13)式更新uk和ωk；

3)利用式(14)更新λ；

(14)

4)规定判定精度e>0，若

3 基于MED-VMD的故障特征提取

当滚动轴承处于早期故障时，故障冲击分量微弱，容易被噪声掩盖，导致故障特征提取困难。振动信号经过MED处理后，能够减弱强背景噪声的影响，突出冲击特性。VMD算法各模态分量的频率中心及带宽在迭代求解中不断变化，以实现振动信号各频域信息分量的自适应的划分，每个模态分量的频带都紧密围绕在中心频率附近，避免了模态混叠、伪分量等问题，便于轴承故障特征的提取。

MED-VMD提取故障特征的具体步骤如下：

1) 确定滚动轴承测点，采集轴承振动信号x(t)。

2) 对x(t)进行MED降噪处理，得到经过最优滤波器处理后的反卷积信号。

3) 采用VMD对反卷积信号进行分解，得到一组变分本征模态分量。

4) 计算各模态分量的峭度值和相关系数，根据峭度准则和相关性最大准则，提取包含故障特征信息最为丰富模态作为敏感分量。

5) 对敏感分量进行Hilbert包络解调，利用傅里叶变换对包络信号做频谱分析，得到敏感分量包络谱。

6) 将包络谱中峰值明显的谱线与滚动轴承故障特征频率的理论计算值做比较，提取故障特征频率。

4 实验分析

在风力发电机组实验台上进行了滚动轴承损伤类故障实验，并通过自行研发的DR-4001高精度信号采集模块测取轴承故障的振动数据。试验台组成部分主要有叶片、主轴承、齿轮箱、高速轴承、发电机等，测试对象是发电机前端高速轴深沟球滚动轴承，轴转速高，承受径向载荷大。实验过程中高速轴的转速恒定不变，采样率fs为10 kHz，采样点数为6 000。分别在轴承的内圈、外圈上切割沟槽来模拟轴承的局部损伤，设置的故障程度均属较轻微的程度。试验中高速轴转速为1 500 r/min时，根据轴承参数和轴承内、外圈以及滚动体故障的特征频率公式，计算得到轴承内圈故障频率为131 Hz，外圈故障频率为87.9 Hz。

4.1 轴承内圈故障分析

传感器采集到的高速滚动轴承内圈故障信号时域波形图如图1(a)所示，由于背景噪声的影响，图中仅可见少量冲击成分。图1(b)为内圈振动信号的包络谱，并没有发现幅值突出的频率成分，说明传统的包络谱分析不能有效提取故障特征。

图1 内圈实验故障信号时域图和包络谱

为了消除背景噪声影响，突出故障冲击脉冲，应用MED算法对图1(a)中仿真信号进行降噪处理，降噪后的信号时域图如图2(a)所示，可以看出信号中噪声成分被部分抑制，冲击成分凸显。对降噪后的信号进行Hilbert变换，得到包络谱如图2(b)所示，图中可以看到幅值突出的频率成分，但是并不能提取出规律性的特征频率，需要对MED降噪后的信号进一步处理。

应用VMD算法对图2(a)中信号进行分解，得到一组不同中心频率的变分模态函数u1～u4，其时域波形如图3所示，可以看出各分量包含明显的冲击成分。在VMD运算时，为保证分解的保真度，τ设为0.3，α设为默认值2 000。

图2 MED处理后的内圈信号时域图和包络谱

图3 内圈实验MED降噪后信号经VMD分解后的结果

正常工况下轴承振动信号的峭度值接近3，而故障时峭度值会显著增大。VMD各模态分量的峭度值和相关系数如表1所示，各分量峭度值明显大于3，说明可能存在故障。相关系数表明各变分模态分量与原信号的相关程度。由表1得，u3的峭度值最大，且其与原信号最为相关，根据峭度准则和相关性准则，选取u3为包含故障信息最为丰富的敏感分量。计算u3的包络谱，如图4所示,可以看出轴承内圈故障特征频率(131 Hz)及其倍频处幅值清晰且突出，表明轴承内圈可能存在局部损伤。

表1 内圈实验MED-VMD模态分量峭度值、相关系数

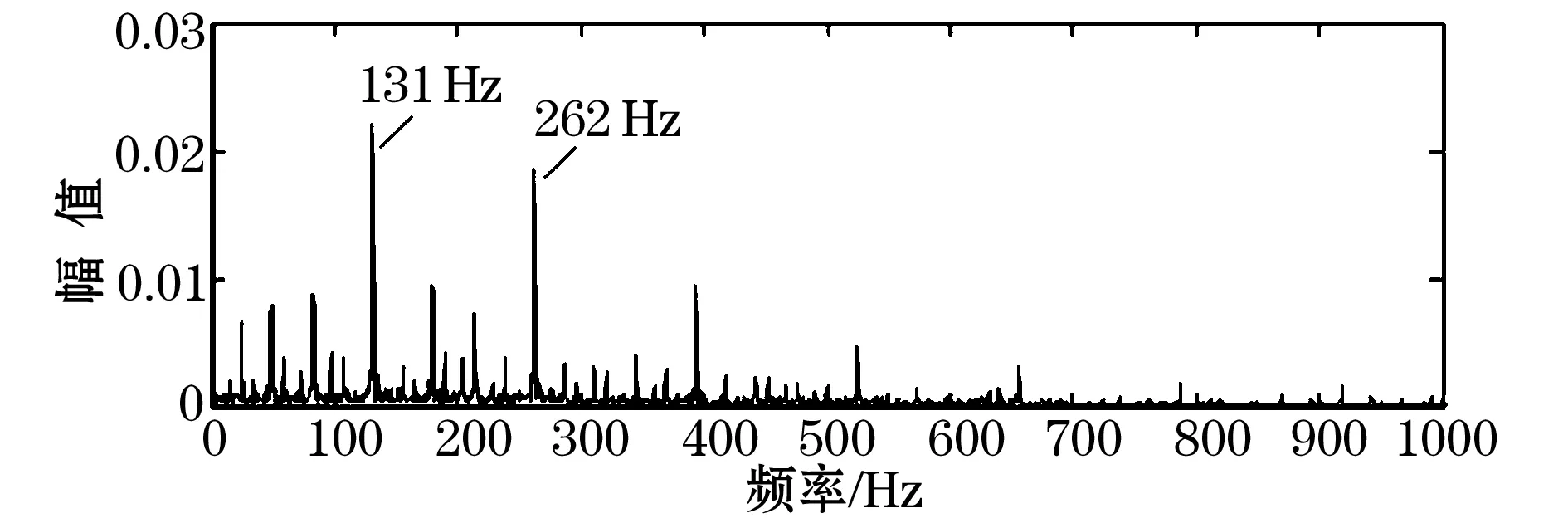
图4 内圈故障实验MED-VMD后u3包络谱

应用MED-EMD算法对振动信号进行处理，并与MED-VMD算法作比较。MED-EMD算法,首先应用EMD对MED降噪后的信号进行分解，得到一组模态分量c1～c8，然后结合峭度和相关性准则，提取敏感模态分量为c4，图5(a)、图5(b)分别显示了c4的时域图和包络谱图。

图5 内圈故障实验MED-EMD算法分析结果，c4

由图5(a)看出，经过MED-EMD分解后的信号故障冲击周期性不明显，且存在模态混叠问题。图5(b)包络谱中含有大量无关频率，故障特征不能有效提取。综合图4，可知此文提出的算法在滚动轴承故障特征提取方面具有一定的优越性。

4.2 轴承外圈故障分析

图6(a)、6(b)显示了电机高速轴承外圈故障实验的振动信号时域图和包络谱。对外圈故障振动信号进行MED降噪并VMD分解，从模态分量组中提取敏感分量为u2，其时域图和包络谱分别如图7(a)、7(b)所示。与内圈故障实验类似，使用此文方法能够很清晰的提取外圈故障特征频率(87.9 Hz)，据此可判断外圈可能存在局部损伤。对比此文算法，图8(a)、8(b)中显示了MED-EMD算法得到的敏感分量c5的时域图和包络谱，存在模态混叠和噪声较多的问题，由此看出此文方法在轴承故障特征频率提取中能够取得良好的效果。

图6 外圈实验故障信号时域图和包络谱

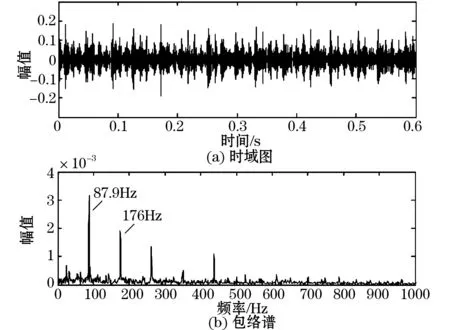
图7 外圈故障实验MED-VMD后的结果，u2

图8 外圈故障试验MED-EMD算法分析结果c5

5 工程案例分析

采用某内蒙风电场采集的风电机组发电机轴承振动数据进行验证分析，选取轴承处于早期故障时的振动数据进行故障特征提取，采样频率为12 800 Hz，采样点数为7 680个，即时长0.6 s的数据，滚动轴承型号为NU2326。采集的振动信号时域波形如图9(a)所示，信号中的冲击特性并不明显，对振动信号进行传统包络谱分析，如图9(b)所示，并没有出现频率突出的故障频率成分。利用MED对振动信号降噪，再利用VMD进行分解，得到一组固有模态分量u1-u4，各分量的峭度值和相关系数如表2所示。

图9 发电机轴承振动信号时域图和包络谱

表2 MED-VMD模态分量峭度值、相关系数

由表2知u2的峭度值最大，且与原信号相关性最大，故对u2进行包络谱分析，如图10(a)所示，图中主要的突出频率为113.7 Hz及其二倍频和三倍频。风电机组发电机转速为1301 r/min，对应转频21.68 Hz，与包络谱中21.8 Hz频率分量非常接近，由于存在测量误差和计算误差，计算得到的特征频率会与包络谱中特征频率存在一定误差。在21.68 Hz转频下，根据轴承参数计算得到的外圈故障特征频率为114.47 Hz，与包络谱中113.7 Hz频率分量十分接近，在误差范围内可以认为113.7 Hz为轴承外圈故障特征频率，且特征频率的高次谐波也比较突出，说明成功提取了轴承外圈故障特征。同时表明轴承外圈可能存在损伤，与风电场检修诊断报告结果一致。

采用MED-EMD算法对振动信号进行处理，提取敏感分量c4并进行包络谱分析，结果如图10(b)所示，包含噪声较多，不能很好的突出故障特征频率。可见，MED-VMD算法能更有效的提取故障特征。

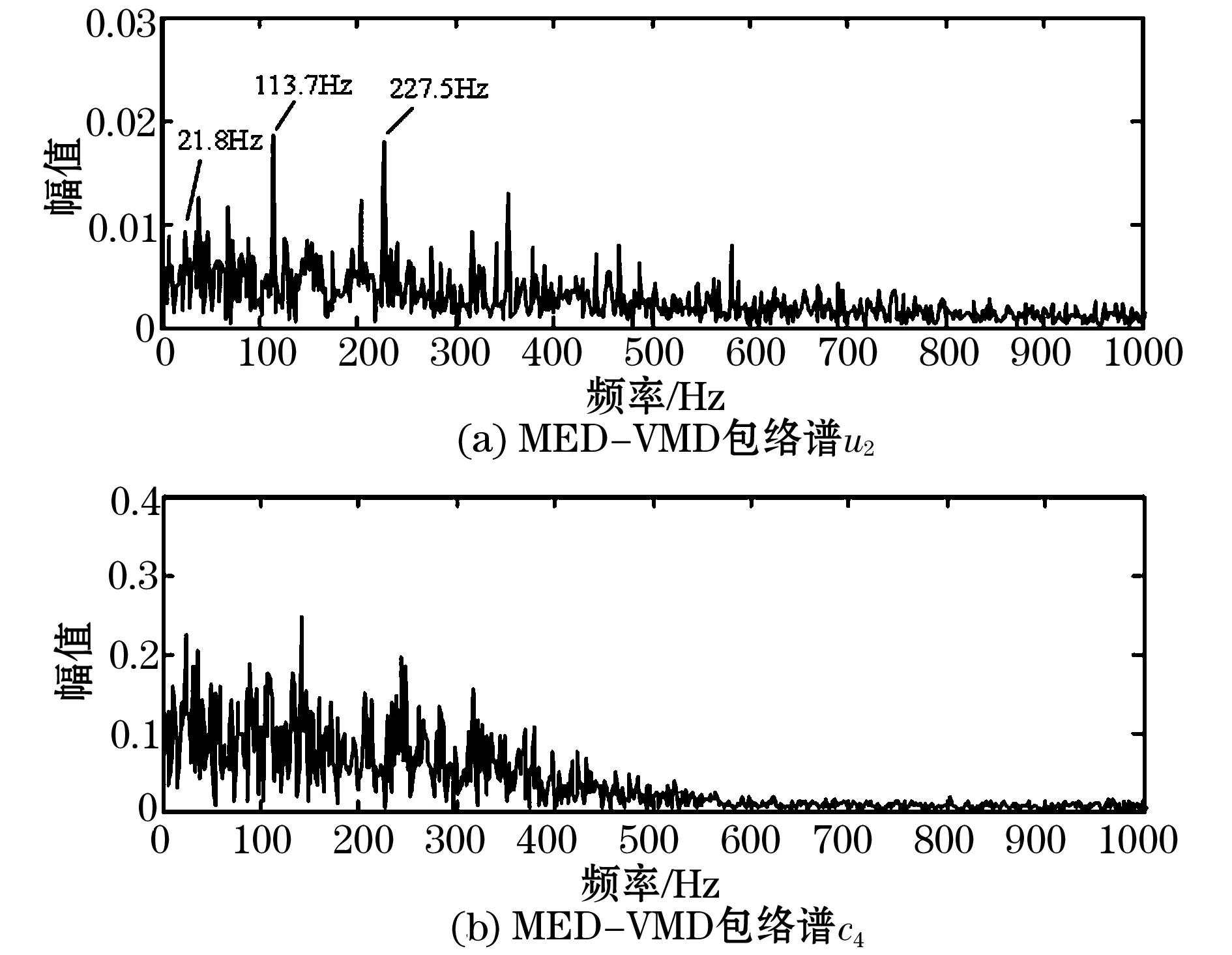
图10 发电机轴承振动信号经MED-VMD和MED-EMD处理后的结果对比

6 结 论

针对风电机组发电机侧滚动轴承运行环境恶劣、易故障，而早期故障特征难以提取的特点，提出了一种基于MED和VMD结合的滚动轴承早期故障特征提取方法。首先利用MED算法减弱噪声影响，突出冲击脉冲，再对降噪后的信号进行VMD并提取敏感分量，最后利用包络谱分析提取故障特征频率。内、外圈故障实验和工程案例分析结果表明,MED-VMD算法能够有效地提取风机发电机滚动轴承的故障特征信息。总体来说，MED-VMD算法对轴承故障特征提取以及故障诊断等相关领域的研究具有一定参考价值。

[1] 赵洪山，郭伟，邵玲，等．基于子空间方法的风机齿轮箱故障预测算法[J]．电力自动化设备，2015，35(3)：27-32．

ZHAO Hongshan，GUO Wei，SHAO Ling，et al．Gearbox fault prediction algorithm based on subspace method for wind turbine[J]．Electric Power Automation Equipment，2015，35(3)：27-32．

[2] 赵洪山，连莎莎，邵玲．基于模型的风电机组变桨距系统故障检测[J]．电网技术，2015，39(2)：440-444．

ZHAO Hongshan，LIAN Shasha，SHAO Ling．A model-based fault detection for variable-pitch system of wind turbines[J]．Power System Technology，2015，39(2)：440-444．

[3] 赵洪山，李浪．基于MCKD-EMD的风电机组轴承早期故障诊断方法[J]．电力自动化设备，2017，37(2)：29-36．

ZHAO Hongshan，LI Lang．Incipient bearing fault diagnosis based on MCKD-EMD for wind turbine[J]．Electric Power Automation Equipment，2017，37(2)：29-36．

[4] 高强，杜小山，范虹，等．滚动轴承故障的EMD诊断方法研究[J]．振动工程学报，2007，20(1)：15-18．

GAO Qiang，DU Xiaoshan，FAN Hong，et al．An empirical mode decomposition based method for rolling bearing fault diagnosis[J]．Journal of Vibration Engineering，2007，20(1)：15-18．

[5] 隋文涛，张丹，Wilson W．基于EMD和MKD的滚动轴承故障诊断方法[J]．振动与冲击，2015，39(9)：55-59;64．

SUI Wentao，ZHANG Dan，Wilson Wang．Fault diagnosis of rolling element bearings based on EMD and MKD[J]．Journal of Vibration and Shock，2015，39(9)：55-59;64．

[6] 胡爱军，马万里，唐贵基．基于集成经验模态分解和峭度准则的滚动轴承故障特征提取方法[J]．中国电机工程学报，2012，32(11)：106-111;153．

HU Aijun，MA Wanli，TANG Guiji．Rolling bearing fault feature extraction method based on ensemble empirical mode decomposition and kurtosis criterion[J]．Proceedings of the CSEE，2012，32(11)：106-111;153．

[7] Liu Huanhuan，Han Minghong．A fault diagnosis method based on local mean decomposition and multi-scale entropy for roller bearings[J]．Mechanism and Machine Theory，2014，75(5)：67-78．

[8] Dragomiretskiy K，Zosso D．Variational mode decomposition[J]．IEEE Transactions on Signal Processing，2014，62(3)：531-544．

[9] 高艳丰，朱永利，闫红艳，等．基于VMD和TEO的高压输电线路雷击故障测距研究[J]．电工技术学报，2016，31(1)：24-33．

GAO Yanfeng，ZHU Yongli，YAN Hongyan，et al．Study on lighting fault locating of high-voltage transmission lines based on VMD and TEO[J]．Transactions of China Electrotechnical Society，2016，31(1)：24-33．

[10] 唐贵基，王晓龙．变分模态分解方法及其在滚动轴承早期故障诊断中的应用[J]．振动工程学报，2016，29(4)：638-648．

TANG Guiji，WANG Xiaolong．Variational mode decomposition method and its application on incipient fault diagnosis of rolling bearing[J]．Journal of Vibration Engineering，2016，29(4)：638-648．

[11] 张伟，白恺，宋鹏，等．基于VMD和奇异值能量差分谱的风机滚动轴承故障特征提取方法[J]．华北电力技术， 2017(3)：59-64．

ZHANG Wei，BAI Kai，SONG Peng，et al．Wind turbine rolling bearing fault feature extraction method based on vmd and singular value energy difference spectrum[J]．North China Electric Power，2017(3)：59-64．

[12] 马增强，李亚超，刘政，等．基于变分模态分解和Teager能量算子的滚动轴承故障特征提取[J]．振动与冲击，2016，35(13)：134-139．

MA Zengqiang，LI Yachao，LIU Zheng，et al．Rolling bearings’ fault feature extraction based on variational mode decomposition and Teager energy operator[J]．Journal of Vibration and Shock，2016，35(13)：134-139．

[13] 张龙，胡俊锋，熊国良．基于MED和SK的滚动轴承循环冲击特征增强[J]．振动、测试与诊断，2017，37(1)：97-101; 201-202．

ZHANG Long，HU Junfeng，XIONG Guoliang．Cyclic shock enhancement by the combination of minimum entropy deconvolution and spectral kurtosis．Journal of Vibration[J]，Measurement&Diagnosis，2017，37(1)：97-101;201-202．

[14] 周士帅，窦东阳，薛斌．基于LMD和MED的滚动轴承故障特征提取方法[J]．农业工程学报，2016，32(23)：70-76．

ZHOU Shishuai，DOU Dongyang，XUE Bin．Fault feature extraction method for rolling element bearings based on LMD and MED Transactions of the Chinese Society of Agricultural Engineering，2016，32(23)：70-76．

[15] He Dan，Wang Xiufeng，Li Shancang，et al．Identification of multiple faults in rotating machinery based on minimum entropy deconvolution combined with spectral kurtosis[J]．Mechanical Systems and Signal Processing，2016，81(12)：235-249.

Extraction method of wind turbine generator rolling bearing fault characteristics based on MED and VMD

Zhang Wei,Zhao Hongshan

(School of Electrical and Electronic Engineering,North China Electric Power University,Baoding 071003,China)

At the early fault of the wind turbine generator rolling bearing, the mechanical vibration signal contains complex information components, which affect the extraction of weak fault signal and make it very difficult to identify the fault. Wind turbine generator rolling bearing exaction method is proposed based on the combination of Minimum Entropy Deconvolution (MED) and Variational Mode Decomposition (VMD). Firstly, the collected vibration signal was denoised by MED algorithm, so as to highlight the fault impact characteristics which is obscured by noise. Then, the VMD algorithm is used to decompose the denoised signal to obtain a series of intrinsic mode functions (IMF) and kurtosis and correlation maximum criterion is selected to contain the most component of information content, namely, the sensitive modal component. Finally, the envelope spectrum of sensitive modal component is analyzed, and the fault characteristic frequency is extracted. The experimental and engineering case analysis results show that the method can effectively extract fault characteristics.

wind turbine generator; rolling bearing; Minimum Entropy Deconvolution (MED); Variational Modal Decomposition (VMD); feature extraction

2017-07-10。

国家科技支撑计划项目(2015BAA06B03)。

张伟(1993—),女，硕士研究生，研究方向为风电机组故障检测与诊断、振动信号处理。

TM315

A

2095-6843(2017)05-0434-07

(编辑李世杰)