单管塔地脚螺栓可靠性设计研究
施柏楠 雷雪峰
(1.江苏省邮电规划设计院有限责任公司,江苏 南京 210019; 2.航空工业成都飞机工业有限责任公司,四川 成都 610092)
单管塔地脚螺栓可靠性设计研究
施柏楠1雷雪峰2
(1.江苏省邮电规划设计院有限责任公司,江苏 南京 210019; 2.航空工业成都飞机工业有限责任公司,四川 成都 610092)
针对通信工程中常用单管塔的地脚螺栓,分析了其在风荷载作用下的效应,建立了整个地脚螺栓群的极限状态方程组,并导出与该方程组等效的可靠概率积分算式,利用数值积分得出在各设计应力比下的地脚螺栓群的可靠指标,结果显示:可靠指标随着设计应力比的增大而线性降低。最后,给出了可供工程设计参考的应力比限值,设计应力比可放宽至1.1。
风荷载,单管塔,地脚螺栓,可靠指标
0 引言
CECS 236∶2008钢结构单管通讯塔技术规程[1]已颁布多年,是通信铁塔常用的设计规范,为指导我国通信铁塔设计做出了巨大贡献。然而该技术规程仍存在争议使用的地方,如在地脚螺栓的设计中,设计人员常采用某小于1的应力比限值来进行设计,设计应力比取1.0可靠性是否足够仍然不得而知,故有必要对其进行可靠度校准。本文旨在确定该技术规程对应的地脚螺栓设计公式在风荷载作用下可靠度水准,并为工程设计提供合理的应力比限值。
1 本文约束条件
为简化分析,本文采用下面两个约束条件来进行可靠性分析:
1)忽略尺寸变异影响,因为尺寸的变异系数相对于材料强度的变异系数、荷载效应变异系数很小[2]。
2)确定单管塔外法兰盘的受力机理:根据CECS 236∶2008钢结构单管通讯塔技术规程相应条文说明,外法兰将实际的受压区形心轴放在离圆心3/4R处。
2 工程常用的设计方法
工程中常采用设计应力比限值来进行地脚螺栓的设计,见式(1)。

(1)
其中,α为设计应力比;σd为锚栓设计应力值;fd为锚栓抗拉强度设计值。
3 抗力的概率分布及统计参数
本文地脚螺栓的材质以工程中常用的Q345为例。抗拉抗力R取正态分布[3],且各地脚螺栓的抗力独立同分布。根据相关资料[4],Q345锚栓的抗拉应力的均值与标准值的比值为1.09,变异系数为0.07。
4 荷载的概率分布及统计参数
在工程结构可靠度分析中,经常假定荷载与荷载效应之间存在近似的线性比例关系,故荷载效应的统计规律可用荷载的统计规律来替代。根据GB 50009—2012建筑结构荷载规范[5]以及文献[6],各种荷载的统计参数见表1。其中,永久荷载为正态分布、可变荷载为极值Ⅰ型分布。

表1 荷载统计参数
根据GBJ 68—1984建筑结构设计统一标准[7],可靠度分析中常采用三种荷载组合:恒+办公楼面可变活载、恒+住宅楼面可变活载、恒+风荷载。由于本工程结构为通信单管塔结构,不存在办公楼可变荷载与住宅可变荷载,且通信铁塔结构起控制作用的为风荷载,故本文只分析恒+风荷载作用下的可靠性问题。
5 荷载效应分析
根据本文的单管塔外法兰盘受力机理(约束条件2),在风荷载随机变量w和自重随机变量G的作用下,对旋转轴取矩,地脚螺栓拉力随机变量Ti为:

(2)
其中,M为风荷载随机变量w引起的弯矩效应随机变量;yi为地脚螺栓距旋转轴的距离;TM为弯矩效应随机变量M引起的地脚螺栓的拉力随机变量;TG为自重随机变量G引起的地脚螺栓的压力随机变量;e为法兰盘对称轴距旋转轴的距离。TM的概率分布类型与变异系数同风荷载的概率分布类型与变异系数,TG的概率分布类型与变异系数同恒载的概率分布类型与变异系数。TM与TG相互独立。由于第i个地脚螺栓与第j个地脚螺栓的拉力随机变量比:
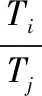
(3)
此比值为常数(本文约束条件1,忽略尺寸的变异),故各地脚螺栓的拉力随机变量线性相关,即相关系数为1。
6 荷载效应密度函数的确定
以插接式单管塔为例,从《通信铁塔标准图集V1.3》中直接读取塔脚弯矩设计值Md,弯矩标准值Mk,竖向力标准值Gk。根据CECS 236∶2008钢结构单管通讯塔技术规程中5.3.3-1式:

(4)
其中,Tdi为各地脚螺栓的设计内力,可计算出对应的应力比为αdi。
根据表1中风荷载的均值与标准值的比值kw以及弯矩的标准值Mk,可得弯矩的均值μM:
μM=kw·Mk
(5)
同理可得TM的均值μTM:
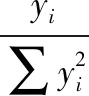
(6)
M,TM的变异系数δM,δTM同表1风荷载的变异系数,为0.193。
同理:可得TG的均值μTG:
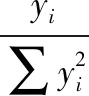
(7)
其中,kG为表1中恒载均值与标准值的比值;TG的变异系数取表1中恒载的变异系数,为0.07。
7 极限状态方程组的建立与可靠指标求解方法
由于单管塔地脚螺栓群的分布特点,最远离旋转轴的几个地脚螺栓受力最大,且受力大小接近,如只考虑受力最大的单个地脚螺栓,则高估了整个地脚螺栓群的可靠性,故有必要考虑地脚螺栓的整体可靠性。
设第i个地脚螺栓独立的极限状态方程为:
Ri-Si=0
(8)
其中,Ri为第i个地脚螺栓的抗力;Si为作用在第i个地脚螺栓的荷载效应,两者均为随机变量。
则整个地脚螺栓群的极限状态方程组为:
(9)
其中,根据前文分析,随机变量Ri与随机变量Rj独立同分布,Ri与Si,Sj相互独立,Si和Sj线性相关。若用传统的可靠度求解方法难以求解该极限状态方程组对应的可靠指标。若设p(x),q(y),H(z)分别为TM的密度函数、TG的密度函数、抗力R的累积分布函数,p(x),q(y)相互独立。则任一TM,TG发生的概率微元:p(x)·q(y)dxdy,对于受力最大的地脚螺栓,满足式(10)条件,使得承载力满足。
z>x-y
(10)
则对于p(x)·q(y)dxdy这一概率微元、受力最大的地脚螺栓,承载力满足的概率为:
[1-H(x-y)]·p(x)·q(y)dxdy
(11)
则整个地脚螺栓群在规定时间内完成规定功能的概率为:
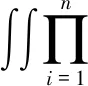
(12)
式(12)与极限状态方程组式(9)等效,式(12)中ymax为受力最大地脚螺栓距真实旋转轴的距离。则最终可靠指标:
β=Φ-1(P)
(13)
其中,Φ-1(.)为标准正态累计分布函数对应的反函数。
8 典型塔形地脚螺栓设计应力比对应的可靠指标
利用matlab数值积分计算式(12)及式(13),针对DGT(C)-45-0.45-3PT3塔型、设计应力比为0.89时,分析单个地脚螺栓可靠指标与地脚螺栓群可靠指标的差别,见表2。

表2 可靠指标与计入可靠指标分析的地脚螺栓数量的关系
根据式(12)的概念分析以及表2的结果,随着计入可靠指标分析的螺栓数量越多,可靠指标越低,地脚螺栓群的可靠指标比受力最大的单个地脚螺栓的可靠指标下降了0.133,当计入数量超过3个时,可靠指标已趋于收敛。故下文的可靠指标计算皆只计入受力最大的3个螺栓。
本文得出常用的0.45风压插接式单管塔标准塔型在不同螺栓设计应力比下的可靠指标,见表3。散点图见图1。

表3 不同应力比下的可靠指标

根据图1,可靠指标的整体趋势随着设计应力比的增大而减小。若将这些散点线性回归拟合成直线,其相关系数[8]可达到0.992 4,可认为可靠指标与设计应力比之间为线性关系,见式(14):
β=-3.060 1α+7.061 4
(14)
根据GB 50068—2001建筑结构可靠度设计统一标准,二级安全等级、延性破坏的构件的可靠指标不应低于3.2,当设计应力比为1.0时,可靠指标为4.001。由于地脚螺栓为单管塔核心受力构件,若人为提高一级安全等级来进行设计,则一级安全等级对应的可靠指标为3.7,求得的设计应力比为:
α=1.098≈1.1
(15)
故根据式(15),在利用CECS 236:2008钢结构单管通讯塔技术规程中5.3.3-1式来进行地脚螺栓设计时,可放宽应力比限值至1.1。或将该技术规程中相关设计公式变更为式(16):
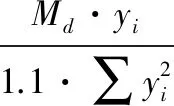
(16)
使用式(16)进行设计时,设计应力比限值为1.0。
9 结语
1)CECS 236:2008钢结构单管通讯塔技术规程相应的地脚螺栓设计公式满足可靠性要求,且其可靠指标超出目标可靠指标0.8;
2)随着计入考虑的地脚螺栓数量的增多,地脚螺栓群的整体可靠指标下降,单个地脚螺栓可靠指标高出地脚螺栓群整体可靠指标0.133;
3)地脚螺栓群承载力可靠指标与设计应力比呈线性关系;
4)按原技术规程中相应的设计公式进行设计时,可放宽设计应力比至1.1,或仍采用1.0设计应力比限值,但此时应采用式(16)的设计公式。
[1] CECS 236∶2008,钢结构单管通讯塔技术规程[S].
[2] 沈在康.混凝土结构设计新规范应用讲评[M].北京:中国建筑工业出版社,1993.
[3] 褚燕风.Q345GJ结构钢材性试验与参数估计[D].重庆:重庆大学,2016.
[4] 张新培.建筑结构可靠度分析与设计[M].北京:科学出版社,2001.
[5] GB 50009—2012,建筑结构荷载规范[S].
[6] 熊 刚.钢结构设计规范GB 50017—2003总体安全度分析[D].重庆:重庆大学,2003.
[7] GBJ 68—1984,建筑结构设计统一标准[S].
[8] 刘嘉焜.应用概率统计[M].北京:科学出版社,2004.
Researchonreliabilitydesignofsteelcommunicationmonopoleanchorbolts
ShiBainan1LeiXuefeng2
(1.JiangsuPosts&TelecommunicationsPlanningandDesigningInstituteCo.,Ltd,Nanjing210019,China; 2.AvicChengduAircraftIndustrial(Group)Co.,Ltd,Chengdu610092,China)
This paper selects the anchor bolts of commonly used steel communication monopole in communication engineering as the research object. We analyze the wind load effect, and establish the limit state equations of the whole anchor bolts, and derive reliable probability integral formula which is equal to the limit state equations. The reliability index of the whole anchor bolts group under different design stress ratio is obtained by numerical integration. The results show that the reliability index decreases linearly with the increase of design stress ratio. At last, this paper gives the limit value of the design stress ratio which can be reference for the engineering design, the design stress ratio can be relaxed to 1.1.
wind load, steel communication monopole, anchor bolt, reliability index
1009-6825(2017)29-0055-03
2017-08-02
施柏楠(1991- ),男,硕士,助理工程师
TU318.1
A

