基于经验正交分解的声速剖面场描述及研究

赵槊,金鑫,邹定杰,李成钢

(1.中海油田服务股份有限公司 物探事业部,天津 300451;2.深圳中海油服深水技术有限公司,深圳 518067)

基于经验正交分解的声速剖面场描述及研究

赵槊1,金鑫1,邹定杰2,李成钢2

(1.中海油田服务股份有限公司 物探事业部,天津 300451;2.深圳中海油服深水技术有限公司,深圳 518067)

本文研究了基于正交分解的声速剖面场的构建原理及过程.并基于MATLAB平台,对实测数据进行正交分解,得到特征值对应的特征向量,即经验正交函数EOF.利用少数几阶EOF重构SSP,并与实测SSP对比,验证了重构声速剖面的可行性及精度问题.

声速剖面;经验正交分解;重构

在海洋领域应用中,获得海洋水声环境参数是非常必要的,而声速剖面SSP(Sound Speed Profile)是其中最重要的参数之一.各种海洋水声参数都会随着时间和空间的变化而变化,由于受外界环境(如温度、盐度、密度、生物群等因素)的影响,SSP会发生较大的变化,特别是在浅水水域中.近年来在学术界中,对海水声速以及影响声速的温度、盐度、密度等因素进行着大量的测试和分析,试图用数学模型描述海水声速的变化规律.

声速剖面测量有直接法和参数反演法.直接法往往采用CTD(Conductivity, Temperature, Depth)声速仪直接测量或间接测量声速剖面.但是,该方法难以快速测量大面积海域的声速剖面,而是需要进行逐点测量,进而测量时间较长,且获得声速剖面具有明显的局限性.而参数反演法监测声速场,方法过于复杂,需有较深的声学理论基础,对海上作业人员来说相对较难.若能采用数学模型,运用描述声速场的相关参数阵或参数,来进行声速剖面场的变化的描述,得到与实际声速剖面比较相符的声速剖面,就可以弥补直接法和参数反演法的不足之处,增加工作效率,降低成本,也减轻了作业人员的理论学习负担.

经验正交函数(Empirical Orthogonal Functions,EOF)是描述SSP最有效的基函数,它能够将SSP在时间和空间变化上分解,把声速参数化,即分解为随时间变化的SSP和随深度变化的SSP.下文提出一种新的基于EOF描述SSP的方法,并利用实测数据基于MATLAB平台进行正交分解,利用3阶EOF来拟合SSP,与实测的SSP进行对比研究.

1 声速剖面场构建原理

EOF分析方法是提取主要数据特征向量的一种方法,它能够把随时间/空间变化的变量分解为不随时间/空间变化的空间函数,以及只依赖时间/空间变化的时间函数部分.基于EOF的SSP就是将声速用正交时间函数和正交深度函数表示,并把声速采样地理坐标作为SSP的权重.

1.1 基于经验正交函数的构建过程

假设一个采样序列中有N个声速剖面,因为采样时受到外界条件的限制,不可能按等距离取样,因此需插值法,插值得到等距离点处(其深度为)的声速值,转化到M个垂直标准层,得到声速矩阵,记为.将声速矩阵用平均声速剖面与声速扰动X来表示,即为,因此扰动X的协方差矩阵.求出此协方差矩阵的特征值矩阵λ和特征向量F,,其特征向量F就是所求的经验正交函数.

每条声速剖面与平均声速剖面之差,即为声速挠动值x:

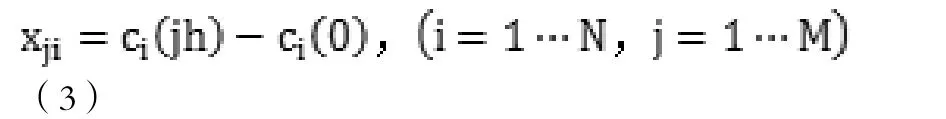
式中,λ为协方差矩阵的特征值,F为与特征值相对应的纵向量,即为特征向量.将特征值λ按大小排序,选取K个特征值较大所对应的特征向量,用该特征向量来表示声速剖面,即所求经验正交函数,则:

因此,重新构建的任意点声速剖面表示为:

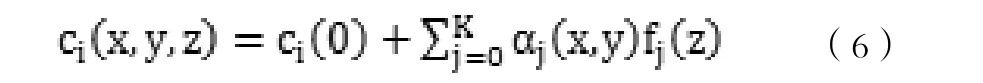
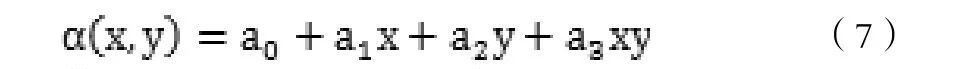
其中a0、a1、a2、a3是待求的参数.则:

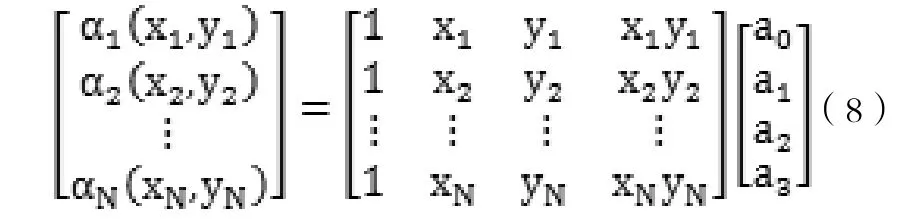
上式表示为:

所以,重新构建的任意点声速剖面进一步表示为:

2.2 误差计算

众所周知,盐度、压力和水温等是海洋声速变化的主要影响因素,在不同的海域情况下,其影响各不相同.用公式(10)构建的声速剖面,具有一定的经验性,其解算出的SSP与实测SSP总会有一定的误差,表示为:

为了衡量基于正交函数分解的声速剖面的准确性,我们用均方根误差的大小来表示:

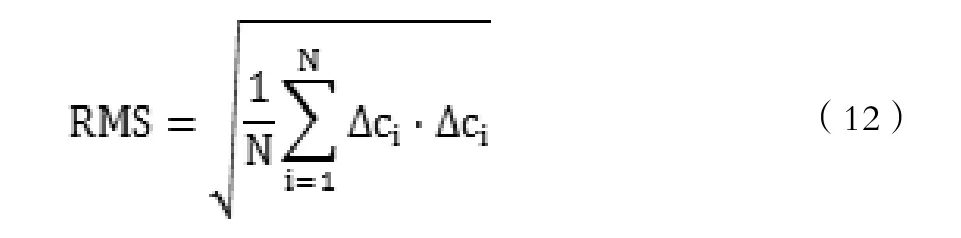
3 试验

在某海域中,使用CTD设备实测,共采样25条声速剖面数据,水深约45米左右.首先对测量的数据进行预处理,包括格式的转换、插值解算等.然后,基于MATLAB系统平台,建立声速矩阵,得到协方差矩阵,求解特征值和特性向量(也即为所确定的EOF).再根据加权系数函数,确定出系数a0、a1、a2、a3参数.最后,根据公式(10)重新构造声速剖面,表示出该区域内任意一点的声速剖面.该数据组的EOF如图1,其协方差矩阵的特征值按大小排列,如表1.

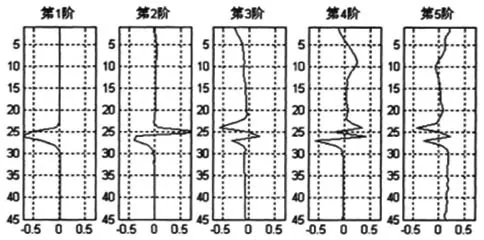
图1 前五阶EOF

表1 特征值

从表中看出,前3个特征值远大于其他特征值.而第1阶特征值较大,进一步说明,第一阶包含了声速剖面场的主要信息,其他阶数是对声速剖面场的细微描述.

我们使用前3阶EOF来分别重构其中1条SSP,并与实测SSP对比.发现重构的SSP与实测的SSP十分相近,其均方根误差RMS分别为0.35m/s(图2).

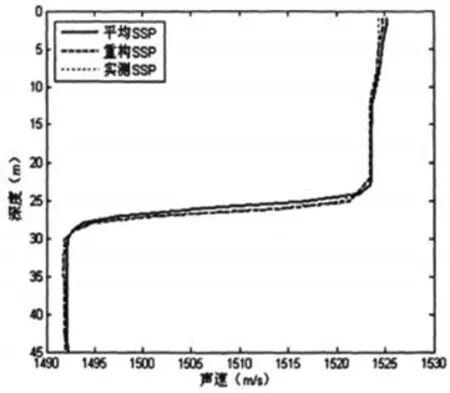
图2 重构的SSP

3 结语

基于EOF重构声速剖面场,最大特征值对应的特征向量基本上包含了声速剖面变化的主要信息,较小特征值对应的特征向量描述了声速剖面的细微变化.

基于正交函数分解构建SSP,具有能快速、精确的重构SSP.由表1数据可以看出前3个特征值远大于其他特征值,所以只需要少数几阶就可以达到重构SSP的目的.

前3阶EOF重构的SSP与实测的SSP十分相近,误差很小.用的阶数越多,拟合的精度越好,针对不同的要求,选择不同的阶数.若精度满足要求的情况下,利用EOF 重构声速剖面场将会增加工作效率，降低作业成本。

TE54

A

1671-0711(2017)11(上)-0143-02