路面结构的路基刚度提高方法
黄拓,昌振东,漆帅
路面结构的路基刚度提高方法
黄拓,昌振东,漆帅
(长沙理工大学交通运输工程学院,湖南长沙,410114)
为满足路面结构对路基刚度的要求,基于弹性半空间和双层弹性体系弯沉等效原则,进行路基刚度补偿设计,揭示路基刚度、加铺材料刚度和加铺层厚度对加铺效果的影响。在大型加速加载试槽中选取一段足尺试验路,铺筑级配碎石刚度补偿层,计算并实测路基顶面当量回弹模量。对典型路面结构进行有限元计算,研究结果表明:按弯沉等效原则计算的路基顶面当量回弹模量理论结果与现场测试结果较吻合,能指导刚度补偿层的设计;当路基当量回弹模量从40 MPa提高至120 MPa时,路面结构的整体刚度提高26.9%,水稳层底的拉应力降低15.1%,说明提高路基刚度,能够有效提高路面结构的耐久性。
路面结构;弯沉等效;路基刚度补偿设计;足尺试验
截至2016年底,我国已通车高速公路里程突破13万km, “十三五”期间还将新建高速公路2万多km,如何提高耐久性、延长路面结构的使用寿命已成为交通领域的重要任务之一[1]。目前,普遍认为高速公路的路基设计寿命应按永久性路基考虑[2],以避免路面结构翻修和重建。在路基修建过程中,回弹模量是表征路基抗变形能力和路面结构设计的重要力学参数,对路面结构的强度、刚度、稳定性、使用性能和寿命起着决定性作用,其取值直接影响着路面结构层的设计厚度和施工质量[3−5]。因此,对于一些回弹模量不满足要求的路基,可加铺一定厚度的模量较高的材料对刚度进行补偿,使路基整体刚度满足设计要求。为此,本文作者以长沙理工大学大型加速加载试槽足尺试验路为依托,选取其中1段,基于刚性承载板作用下弹性半空间和双层弹性体系弯沉等效的原则,对路基进行刚度补偿层设计。在此基础上,实测级配碎石的回弹模量,以级配碎石作为刚度补偿层对路基进行加铺,并采用有限元计算程序分析路基刚度对路面结构耐久性的影响,以便为路基加铺层设计提供试验及理论参考。
1 基于弯沉等效的路基刚度补偿 设计方法
1.1 等效原则的选取
所谓刚度补偿层,是指在填筑的土基顶面,用压实性好、回弹模量高且具有良好水稳定性的砾石土等填料铺筑一定厚度的上覆层,使路基顶面的回弹模量达到路面设计要求[6−7]。路基顶面当量回弹模量是反映路基顶面作用竖向荷载时路基整体竖向受力与竖向可恢复变形(统称弯沉)之间关系的平均值,可以按照某种物理量(弯沉、弯拉应力、弯拉应变)相等的原则,将多层结构等效为半无限体时得到的地基综合模 量[8−12]。由于弯沉检测简单易行,在路面设计及施工中经常采用,因此,本文以弯沉为等效指标进行刚度补偿设计。


(a) 双层弹性体系;(b) 弹性半空间
双层弹性体系在圆形刚性承载板作用下位移计算公式为


式中:为刚性承载板作用下的垂直位移;为泊松比;为平均单位压力;为承载板半径;为回弹模量;,,和为积分参数;和为函数;J0为0阶贝塞尔函数;上标“v”表示垂直荷载下的物理量;表示层位号。
弹性半空间体在圆形刚性承载板作用下位移计算公式为


1.2 影响刚度补偿效果的因素
1.2.1路基刚度及加铺层厚度的影响

从图2可知:在路基上铺筑刚度补偿层,随着路基刚度和加铺层厚度增加,等效弹性半空间顶面当量回弹模量以增幅逐渐减小的趋势增大,然后逐渐趋于稳定,其值接近加铺层材料的刚度;当路基刚度不变,加铺层厚度从0 cm增加到40 cm时,刚度补偿效果最明显;当加铺厚度为40 cm,路基刚度从20 MPa增加到100 MPa时,顶面当量回弹模量增加量由2.61倍变为0.58倍,其增长速度逐渐减小,且路基刚度越大,加铺相同厚度的材料后其当量回弹模量越高:因此,适当提高路基的刚度与加铺层材料的厚度,可以起到明显的刚度提高效果。在工程应用中,应根据土基模量选取加铺层厚度。从工程经济性角度分析,当路基顶面回弹模量为20 MPa时,铺设40 cm级配碎石造价为45元/m2,模量可提高约50%。若采用排水固结法,模量提高50%,造价约为80元/m2。因此,铺筑级配碎石具有明显的经济效益。

土基模量/ MPa:1—20;2—30;3—40;4—50;5—60;6—70;7—80;8—90;9—100。
1.2.2 加铺层厚度及刚度的影响

从图3可以看出:当双层体系土基模量为40 MPa时,随着加铺层厚度和刚度增大,等效弹性半空间顶面当量回弹模量以增幅逐渐减小的趋势增加,然后逐渐趋于稳定,接近于加铺层材料的刚度,且等效弹性半空间的顶面当量回弹模量在加铺层厚度由0 cm增加到40 cm时增幅较快,随后逐渐放缓并趋于加铺层材料的模量;随着加铺层刚度增大,顶面当量回弹模量的相对增长速度逐渐变大。因此,适当增大加铺层刚度和厚度,对提高刚度的效果更明显。
1.2.3 弯沉变化规律

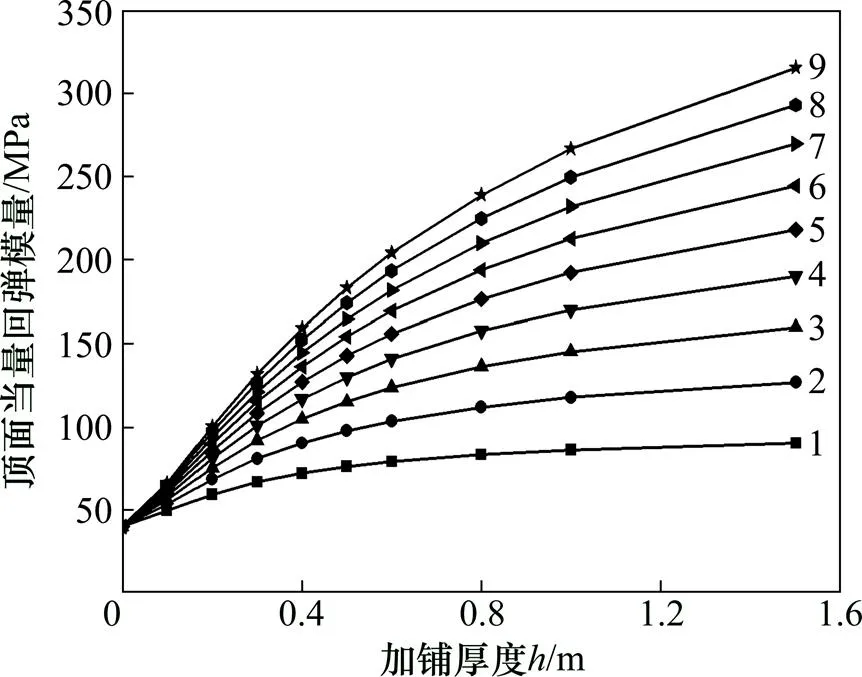
加铺层材料模量/MPa:1—100;2—150;3—200;4—250;5—300;6—350;7—400;8—450;9—500。

(a) 弹性半空间;(b) E0=40 MPa的双层弹性体系
2 刚度补偿设计方法的足尺试验 验证
2.1 刚度与加铺层厚度的关系验证
为了验证刚度补偿方法的准确性,结合长沙理工大学大型加速加载试槽的建设,在长为9 m、宽为5 m试槽中的一段路基上加铺级配碎石,试槽中心线每 3 m布置1个测点,其具体位置见图5。

图5 承载板测试位置
承载板测试路基及加铺层模量的步骤如下:1) 现场标定固定测点;2) 清洁测点表面石粒,摆放承载板,利用细砂调平承载板;3) 调整标准车使加劲梁的承载板中心垂直对准;4) 安放千斤顶和弯沉仪,当承载板与千斤顶之间的距离偏大时可利用垫块调整;5) 千斤顶加载0.05 MPa进行预压,时间为1 min左右,使承载板与结构层紧密接触;6) 逐级加载千斤顶并卸载,每级增加荷载0.1 MPa,读取加载和卸载前、后百分表变形(若2台弯沉仪百分表读取的变形相对误差超过30%,则需对该点进行重测);7) 根据承载板法的加压荷载和测得的回弹变形,利用以下公式计算该点的回弹模量b:

其中:p为对应第级荷载,kN;l为测试得到的回弹变形,0.01 mm;为承载板直径,30 mm;为泊松比。测试点位为K19.5,K22.5和K25.5,路基回弹模量实测值为40.1 MPa。级配碎石参照JTG D50—2006中的级配范围,采用骨架密实型级配进行测试,结果如表1所示。按照JTG-E51—2009中承载板法[15−16]测试其回弹模量,步骤为:成型并安装试件;预压、分级加载测定回弹变形量;将分级加载的应力除以回弹变形量得到回弹模量。5组平行试验测得的静回弹模量为201.7 MPa。土基上铺筑级配碎石刚度补偿层的顶面当量回弹模量理论值与试验值的对比见表2。

表1 级配碎石设计级配

表2 路基铺筑刚度补偿层后模量实测值与理论值对比
由表2可知:路基铺筑级配碎石层后刚度的理论值与实测值之间的相对误差低于10%,较好地验证了刚度补偿设计方法的科学性。
2.2 刚度补偿效果验证
为了研究刚度变化对路面结构整体性能的影响,需将加铺层顶面的当量回弹模量提高至60 MPa左右。如图4所示,相当于直径为30 cm、板底荷载平均集度为0.7 MPa的刚性承载板作用下路基顶面弯沉=241.2(0.01 mm);同时,考虑到施工的控制,据表3,可在原有路基顶面加铺15 cm、模量为200 MPa的级配碎石层进行刚度补偿。通过现场加铺及压实后,进行承载板现场测试,结果见表3。

表3 基于弯沉等效原则的刚度补偿效果验证
由表3可知:在模量为40.1 MPa的路基上铺筑15 cm的级配碎石层后,理论值与实测值之间的相对误差为21.4%。考虑到试槽建设期间一直处于阴雨天气,导致试槽内土质含水量升高,双层加铺结构的整体刚度有所下降。含水率探头测得试槽内部含水率与附近土质的含水量接近,其含水量增高2%左右。在该条件下,用承载板法测得试槽附近土基回弹模量下降约13%。若剔除环境因素的影响,回弹模量理论值与实测值较接近。
3 对路面结构的影响
为了研究路基刚度对路面结构的影响,选取如表4所示的典型路面结构及参数。以双圆均布荷载作用下的弹性层状体系作为结构响应计算的力学模型,以弹性模量为计算参数,通过有限元程序计算典型路面结构的弯沉及层底拉应力,结果见图6。由于足尺试槽长为9 m,宽为5 m,其尺寸足够大,且测试点位于试槽中线位置,两边约束对其影响不大,故可将路面结构当作弹性层状体系进行计算。
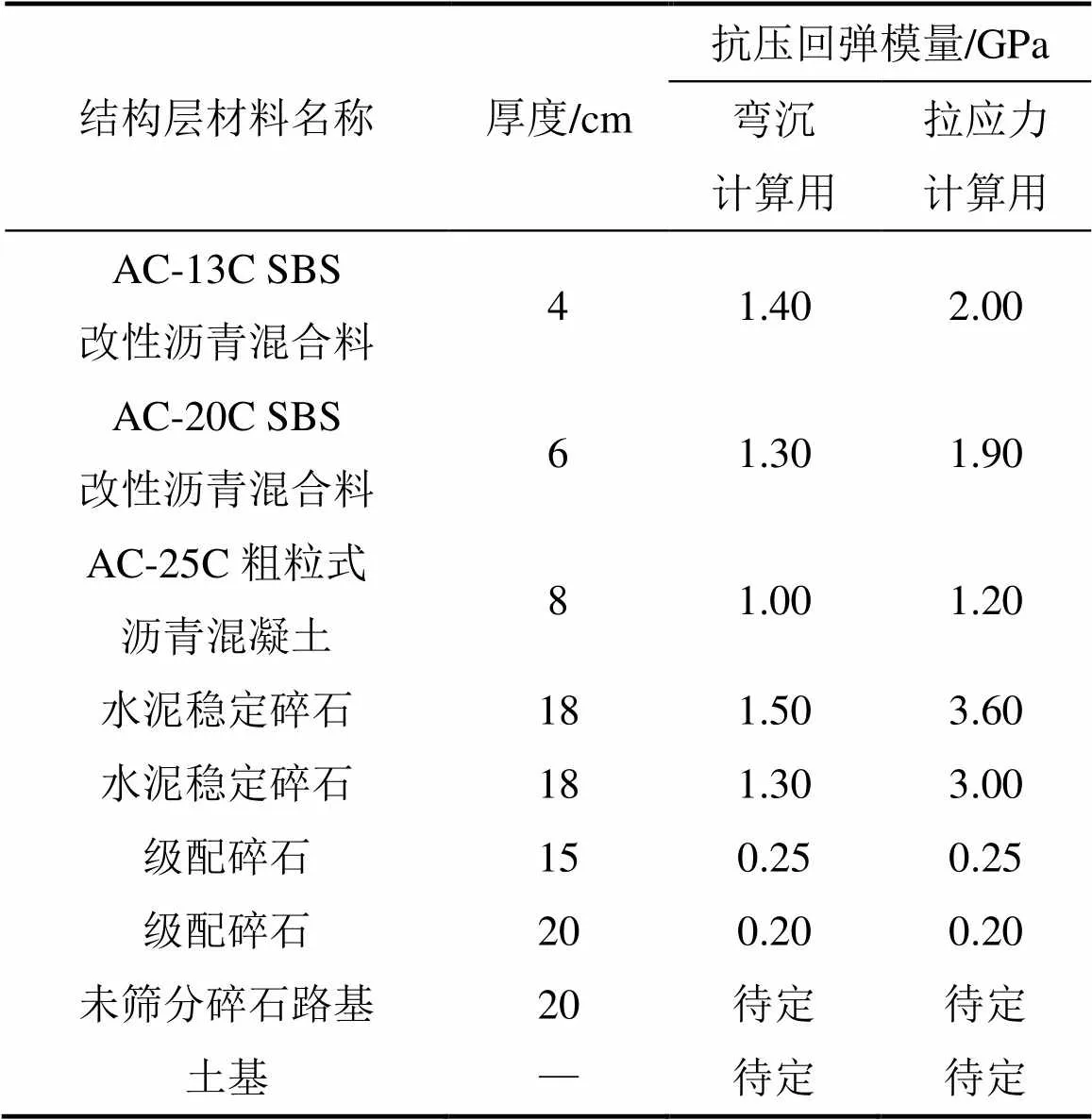
表4 典型的路面结构及参数
注:未筛分碎石不单独作为结构层,而作为土基的精加工层
从图6可知:随着路基当量回弹模量增大,路面结构的弯沉逐渐减小,整体刚度逐渐增大;当量回弹模量从40 MPa提高至60 MPa时,整体刚度提高12.7%;当量回弹模量达120 MPa时,整体刚度提高26.9%。水稳层底的最大拉应力亦随路基当量回弹模量的增大而逐渐减小,当量回弹模量从40 MPa提高至60 MPa,层底拉应力减小5.7%;当量回弹模量达到120 MPa时,层底拉应力减小15.1%。由此可见:增大路基模量不仅可以提高路面结构的整体刚度,而且可以减少由拉应力导致的基层底部开裂及反射裂缝的发生,提高路面结构的耐久性。

(a) 对弯沉的影响;(b) 对水稳层底最大拉应力的影响
4 结论
1) 提出了路面结构的路基刚度补偿方法,揭示了刚度补偿效果随路基刚度、加铺层刚度和厚度增大而提高的规律;根据双层弹性体系和等效弹性半空间弯沉等效的原则,给出了确定刚度补偿层材料和厚度的方法。
2) 在足尺试验试槽的铺筑过程中,通过承载板试验实测了加铺层顶面的当量回弹模量,其实测值与理论值之间的误差较接近,验证了路基刚度补偿方法的准确性。
3) 当路基当量回弹模量从40 MPa提高至120 MPa时,路面结构的整体刚度提高26.9%,水稳层底的拉应力降低15.1%。可见提高路基的刚度,既可提高路面结构的整体刚度,又能减小水稳层底的拉应力,能够提高路面结构的耐久性。
4) 本文虽然通过现场实测验证了路基刚度提高设计方法的准确性,为路基的合理设计提供了理论及试验参考,但仅测试了足尺试槽中的一段,而未开展全面足尺试验。这有待于进一步研究。
[1] 黄拓. 沥青混合料三轴试验方法及破坏准则研究[D]. 长沙: 长沙理工大学交通运输工程学院, 2013: 1−9. HUANG Tuo. Study on triaxial test method and failure criterion of asphalt mixture[D]. Changsha: Changsha University of Science and Technology. School of Traffic and Transportation Engineering, 2013: 1−9.
[2] 郑健龙. 基于结构层寿命递增的耐久性沥青路面设计新思想[J]. 中国公路学报, 2014, 27(1): 1−7. ZHENG Jianlong. New structure design of durable asphalt pavement based on life increment[J]. China Journal of Highway and Transport, 2014, 27(1): 1−7.
[3] JTG D50—2006, 公路沥青路面设计规范[S].JTG D50—2006, Specifications for design of highway asphalt pavement[S].
[4] 查旭东. PFWD 快速检测路基模量研究[J]. 公路交通科技, 2008, 25(1): 26−30. ZHA Xudong. Study of rapid test of subgrade modulus with PFWD[J]. Journal of Highway and Transportation Research and Development, 2008, 25(1): 26−30.
[5] 陈湘亮, 王永和, 王灿辉. 泥质粉砂岩改良土路基填料适宜性试验分析[J]. 中南大学学报(自然科学版), 2013, 44(10): 4287−4293. CHEN Xiangliang, WANG Yonghe, WANG Canhui. Experimental study of suitability of argillaceous siltstone improved soil as filling for subgrade[J]. Journal of Central South University (Science and Technology), 2013, 44(10): 4287−4293.
[6] 郑健龙. 公路膨胀土工程理论与技术[M]. 北京: 人民交通出版社, 2013: 1−11.ZHENG Jianlong. The theory and technology for highway expansive soil engineering[M]. Beijing: China Communications, 2013: 1−11.
[7] 郑健龙, 张锐. 公路膨胀土路基变形预测与控制方法[J]. 中国公路学报, 2015, 28(3): 1−10. ZHENG Jianlong, ZHANG Rui. Prediction and control method for deformation of highway expansive soil subgrade[J]. China Journal of Highway and Transport, 2015, 28(3): 1−10.
[8] 谈至明, 王力. 基于弯拉应力等效的地基当量回弹模量[J]. 公路交通科技, 2015, 32(3): 46−50. TAN Zhiming, WANG Li. Equivalent resilient modulus of subgrade based on principle of flexural-tensile stress equivalence[J]. Journal of Highway and Transportation Research and Development, 2015, 32(3): 46−50.
[9] ASLI C, FENG Z Q, PORCHER G, et al. Back-calculation of elastic modulus of soil and subgrade from portable falling weight deflectometer measurements[J]. Engineering Structures, 2012, 34(1): 1−7.
[10] 吁新华, 谈至明, 沥青路面结构层弯拉应力与应变的近似计算[J]. 同济大学学报(自然科学版), 2012, 40(6): 849−853. YU Xinhua, TAN Zhiming. Approximate calculation of flexural stresses and tensile strains in asphalt pavements[J]. Journal of Tongji University (Natural Science Edition), 2012, 40(6): 849−853.
[11] 姜爱锋, 姚祖康. 路面结构中地基顶面当量回弹模量的换算[J]. 同济大学学报(自然科学版), 2001, 29(5): 536−540. JIANG Aifeng, YAO Zukang. Calculation of surface equivalent modulus of subgrade in the pavement structure[J]. Journal of Tongji University (Natural Science Edition), 2001, 29(5): 536−540.
[12] 蒋应军, 戴经梁, 陈忠达. 不同等效原则的基层顶面当量回弹模量算法[J]. 长安大学学报(自然科学版), 2005, 25(3): 1−6. JIANG Yingjun, DAI Jingliang, CHEN Zhongda. Calculation method of equivalent modulus of elasticity of foundation under principles of different equivalence[J]. Journal of Chang’an University (Natural Science Edition), 2005, 25(3): 1−6.
[13] 郭大智, 冯大成. 层状弹性体系力学[M]. 哈尔滨: 哈尔滨工业大学出版社, 2001: 21−40.GUO Dazhi, FENG Dacheng. Layered elastic system mechanics[M]. Harbin: Harbin Industrial University Press, 2001: 21−40.
[14] 朱照宏, 王秉纲, 郭大智. 路面力学计算[M]. 北京: 人民交通出版社, 1985: 34−50. ZHU Zhaohong, WANG Binggang, GUO Dazhi. Mechanics calculation of pavement[M]. Beijing: China Communications, 1985: 34−50.
[15] 周科峰, 李宇峙. 考虑加载速率的级配碎石三轴压缩强度特性[J]. 中南大学学报(自然科学版), 2015, 46(7): 2613−2619. ZHOU Kefeng, LI Yuzhi. Characteristic of triaxial compressive strength of grading macadam considering loading velocity[J]. Journal of Central South University (Science and Technology), 2015, 46(7): 2613−2619.
[16] 杨勇. 级配碎石刚度过渡层动回弹模量特性研究[D]. 长沙: 长沙理工大学交通运输工程学院, 2016: 34−38. YANG Yong. Research on Characteristics of dynamic resilient modulus of stiffness transition layer for graded crushed rock[D]. Changsha: Changsha University of Science & Technology. School of Traffic and Transportation Engineering, 2016: 34−38.
(编辑 陈灿华)
Promotion method of subgrade stiffness for pavement structure
HUANG Tuo, CHANG Zhendong, QI Shuai
(School of Traffic and Transportation Engineering,Changsha University of Science & Technology, Changsha 410114, China)
In order to meet the requirements of subgrade stiffness for pavement structure, the stiffness compensation design of subgrade was carried out based on deflection equivalent principle of elastic half-space and double-layer elastic system. And the influence of subgrade stiffness, stiffness and thickness of the overlay on the stiffness compensation effect was revealed. A full scale test road was selected in the large accelerated loading field, and the graded crushed stone stiffness compensation layer was paved on the subgrade. Besides, the equivalent resilient modulus at the top of the subgrade was tested and calculated. The finite element calculation was carried to typical pavement structure. The results show that the modulus calculated by deflection equivalent principle is in good accordance with the field test result, which can provide guidance for the design of stiffness compensation layer. When equivalent resilient modulus of subgrade increases from 40 MPa to 120 MPa, the stiffness of pavement structure increases by 26.9%, and the tensile stress at the bottom of cement stabilized subbase decreases by 15.1%. Therefore, improving the stiffness of subgrade can effectively improve the durability of pavement structure.
pavement structure; deflection equivalent; subgrade stiffness compensation design; full scale test
10.11817/j.issn.1672−7207.2017.10.030
U414
A
1672−7207(2017)10−2777−06
2017−03−10;
修回日期:2017−05−12
国家自然科学基金资助项目(51608055);湖南省自然科学基金资助项目(2017JJ3337);湖南省教育厅项目(16C0051);交通运输部建设科技项目(2015318825120);长沙市科技计划项目(Kq1701078)(Project(51608055) supported by the National Natural Science Foundation of China; Project(2017JJ3337) supported by the Natural Science Foundation of Hunan Province; Project(16C0051) supported by the Education Department of Hunan Province; Project(2015318825120) supported by Construction Project of Science and Technology of Ministry of Transport); Project(Kq1701078) supported by the Planned Science and Technology Project of Changsha City)
黄拓,博士,讲师,从事道路结构与新材料研究;E-mail:huangtuomao@163.com

