深部高应力软岩巷道注浆时机优化分析
孟庆彬,韩立军,王琦,张建,范加冬,聂军委,文圣勇
深部高应力软岩巷道注浆时机优化分析
孟庆彬1,韩立军1,王琦2,张建1,范加冬1,聂军委1,文圣勇1
(1. 中国矿业大学深部岩土力学与地下工程国家重点实验室,江苏徐州,221116;2. 山东大学岩土与结构工程研究中心,山东济南,250061)
基于支护−围岩共同作用原理分析,揭示朱集西煤矿深部高应力软岩巷道围岩收敛变形与支护强度及围岩自承力的变化关系,获得巷道围岩位移与支护强度的关系曲线。采用FLAC3D内嵌的Fish语言编程,提取巷道围岩塑性区、拉伸破坏区及剪切破坏区体积数,揭示不同岩性与埋深条件下巷道围岩变形和塑性区扩展随应力释放率的演化规律,再现巷道围岩从局部破坏直至整体失稳破坏的演化过程,提出以应力释放率阈值作为判定注浆时机的指标。研究结果表明:确定当围岩变形量为150 mm时,实现存储于围岩内变形能的充分释放及围岩自承力的最大利用。采用应力释放率阈值60%和围岩变形量150 mm作为判定注浆时机的指标是合理的,两者可相互验证。提出“锚网索喷+注浆+底板锚注”联合支护技术方案,解决了深部高应力软岩巷道支护难题,验证了所确定的注浆时机是合理、可行的。
深部高应力;软岩巷道;注浆时机;应力释放率;围岩−支护特征曲线
能源是国家经济发展的物质基础,随着我国经济的高速发展,对煤炭资源的需求量急剧增加,浅部资源已趋于枯竭,煤炭开采深度不断增加,已逐渐进入深部开采阶段[1−3]。深部岩体处于复杂的工程与地质条件下,造成深部软岩巷道矿压显现剧烈、围岩变形和破坏严重,单一的支护形式难以维持深部软岩巷道围岩的稳定,常采用锚杆、锚索与注浆相结合的联合支护形式[4−7]。研究表明[8],处于塑性状态的软岩巷道围岩仍具有一定的承载力,可通过变形将存储于围岩内的变形能释放出来,以降低支护强度,这需要确定合理的支护时机,适时支护可使维持巷道围岩稳定所需的支护抗力最小,亦可降低支护成本。若能在巷道围岩变形量大部分或全部释放后再施加支护结构,则此时所需提供的支护抗力最小,支护也较为经济[9]。支护时机的选择对软岩巷道支护效果影响较大,最佳支护时机的确定,应以“使巷道围岩释放应力与其自承力达到最佳匹配”为依据,这样既能充分释放存储于围岩内的变形能而降低支护强度,又能最大程度利用围岩体的自承力,这是新奥法的核心思想[10]。国内外研究者进行了一定的理论与工程研究,何满潮等[8]基于理论分析,定义了最佳支护时间的力学含义。陆银龙等[11]综合数值模拟和现场监测分析,提出了判定软岩巷道最佳锚注支护时机的方法。王小平[12]揭示了巷道围岩变形随时间的变化规律,确定了巷道合理支护时间。孙晓明等[13]针对深部巷道围岩在开挖与支护时所表现出的非线性力学过程特性,确定了实现锚网索耦合支护时空耦合的最佳二次支护时间。王祥秋等[14]采用位移反分析方法研究了圆形巷道的黏弹性变形规律,给出了确定软岩巷道合理支护时间的方法。屈延嗣等[15]采用lsqcurvefit函数对巷道变形监测数据进行了最小二乘拟合,并结合现场监测的变形速率得出了二次支护时机。但目前对深部高应力软岩巷道注浆时机的研究尚且不够深入,本文作者以淮南矿区千米深井朱集西煤矿为工程背景,基于理论分析、数值计算与工业性试验等综合技术手段,研究深部高应力软岩巷道注浆合理时机的确定方法,探讨深部高应力软岩巷道支护对策与围岩控制技术方案,为类似巷道支护提供借鉴。
1 软岩巷道合理注浆时机的理论 分析
注浆支护时机,即锚索与注浆组成的二次支护与锚网喷初次支护的时间间隔。若注浆过早,则此时巷道围岩处于变形破裂的发展阶段。一方面,围岩体裂隙开度较小,颗粒浆液难以注入,注浆效果较差;另一方面,因开挖扰动产生的二次应力场会导致注浆加固岩体的再破坏,造成注浆加固失败[11]。若注浆过晚,则巷道围岩变形破坏严重,已丧失承载力,虽然围岩体裂隙开度较大,浆液易注入,但围岩体与初次支护结构已失稳破坏,此时注浆已无意义,即丧失了最佳的注浆时机。因此,选择合理的注浆时机至关重要。
1.1 支护−围岩共同作用原理分析
软岩巷道支护体包括柔性支护与刚性支护[16],经典的“支护−围岩”共同作用原理表明了支护强度与围岩变形之间的关系[17],如图1所示。
软岩巷道不合理的支护设计可分为3类[16, 18]:支护特性曲线1,支护时机过早,围岩内的变形能未充分释放,所需要的支护强度较高,且自身刚度过大,很难实现与围岩的共同作用;支护特性曲线2,支护时机过晚,围岩内的变形能释放较为充分,但支护体刚度过小,导致围岩变形过而失稳破坏;支护特性曲线3,支护时机适当,但支护强度较低,难以控制巷道围岩的变形,支护效果不理想。根据支护特性曲线的分析,软岩巷道的支护效果取决于支护强度和围岩变形量。由于软岩巷道塑性区范围较大,巷道围岩出现破裂后其自承力不断衰减,若未采取合理的支护结构限制其变形,则围岩破坏范围不断扩大,对于支护强度的要求更高。

1—支护时机过早;2—支护时机过晚;3—支护时机适当。
1.2 考虑围岩自承能力的支护−位移曲线
根据新奥法理念[10],巷道开挖后应允许围岩产生适量变形,以使围岩内的变形能充分释放;应充分发挥围岩的自承载作用,与支护结构形成共同承载体。通过围岩稳定性弹塑性分析,可求得巷道围岩收敛−约束曲线[18−19];采用塌落拱理论可获得围岩的自承力[20],通过计算得到的松动圈范围内的围岩自承力随围岩变形的变化曲线[18],如图2所示。
由图2可知:随着巷道围岩位移量的增加,储存于围岩内的变形能不断释放,维持围岩稳定所需的支护强度也逐渐降低;随着巷道围岩位移增加,松动圈范围内的围岩自承力随之衰减;为了维持巷道围岩的稳定状态,围岩自承力衰减量可通过提高支护强度来补偿。由巷道围岩位移与支护强度关系曲线可知:巷道开挖初期采用柔性支护,允许围岩产生适当的位移可有效地降低支护强度,当围岩变形量超过150 mm后,围岩变形破坏程度较大造成支护强度剧烈增加。因此,可以确定合理的注浆时机为围岩位移达到150 mm时,其上限不超过巷道围岩预留变形量200 mm。若巷道围岩变形超过该值,由于围岩变形过大导致自承力降低,所需提供的支护强度增加。

1—巷道围岩收敛−约束曲线;2—巷道围岩自承力衰减曲线;3—巷道围岩位移−支护强度关系曲线。
2 基于应力释放率的注浆时机确定
采用FLAC3D内嵌的Fish 语言编程,根据开挖卸载应力释放率来计算开挖荷载等效节点力,将等效节点力施加于模型所有节点的3个方向上,然后计算当前模型直至平衡结束,同时提取数值计算过程中的巷道围岩塑性区、拉伸破坏区及剪切破坏区体积数。数值计算边界条件:限制模型底部及侧向位移,在上表面施加自重应力,模拟上覆岩层自重;建立模型区域的长×宽×高为60 m×60 m×60 m,共划分276 000个单元,286 761个节点;煤矿深部巷道围岩体物理力学参数取值见表1[4],采用Mohr-Coulomb破坏准则。
2.1 不同岩性条件下巷道围岩变形与破坏特征分析
取巷道埋深=1 000 m,围岩等级为Ⅰ,Ⅱ,Ⅲ,Ⅳ和Ⅴ类,计算时按5%的等级释放荷载,累计完成20次应力释放。不同岩性条件下巷道围岩变形曲线如图3所示;以Ⅴ类围岩为例,巷道围岩变形破坏演化过程如图4所示,不同岩性条件下巷道围岩塑性区体积曲线如图5所示,不同应力释放率条件下巷道围岩位移见表2。
2.1.1 巷道围岩位移演化规律分析
由图3和表2可知:在同一岩性条件下,随着应力释放率增加,巷道围岩变形量随之增大,围岩变形量与变形增量基本呈现出“底板底臌量>顶板下沉量>两帮内挤量”的演化规律,而围岩变形量增幅呈现出“顶板下沉量>两帮内挤量>底板底臌量”的演化规律。
在相同应力释放率的条件下,随着岩性恶化,围岩变形量随之增加。以应力释放率=60%为例,当为Ⅰ类围岩时,顶板下沉量为28.65 mm;当为Ⅱ类围岩时,顶板下沉量为36.52 mm,变形增量为7.87 mm,变形量增幅为27.46%;当为Ⅲ类围岩时,顶板下沉量为71.34 mm,变形增量为42.68 mm,变形量增幅为148.98%;当为Ⅳ类围岩时,顶板下沉量为185.86 mm,变形增量为157.21 mm,变形量增幅为548.70%;当为Ⅴ类围岩时,顶板下沉量为371.40 mm,变形增量为342.75 mm,变形量增幅为1196.29%。以上结果表明:随着岩性恶化,巷道围岩变形量与变形增量随之增大,存储于巷道围岩内的变形能不断释放,即巷道围岩体中的应力不断降低。

表1 煤矿深部巷道围岩体物理力学参数取值[4]
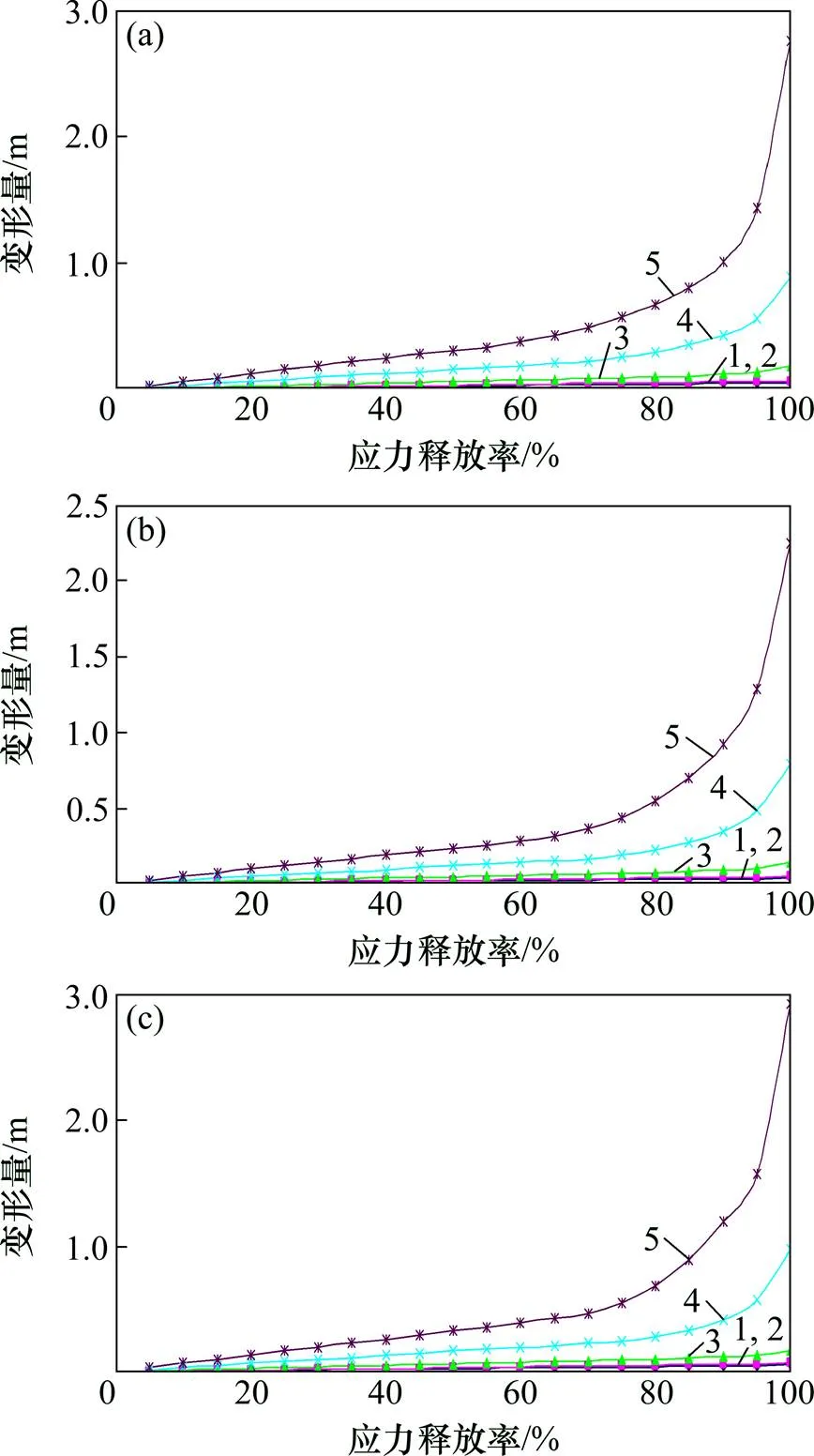
(a) 顶板下沉量;(b) 帮部内挤量;(c) 底板底臌量
2.1.2 巷道围岩变形破坏演化过程分析
在地层中开挖巷道后,原有岩体中的应力平衡状态被打破,在巷道周边产生应力重分布,形成二次应力场,并在巷道周边局部位置处产生应力集中现象,若岩体承受的荷载超过其抗压或抗拉强度,则岩体产生屈服破坏;巷道围岩不同位置处的岩体相继破坏,并相互连接贯穿,形成较大的破裂面,最终导致巷道围岩失稳破坏[19−20]。巷道围岩的变形破坏是一个渐进的过程,随着围岩变形量增加,其损伤破坏范围不断增大,直至围岩产生冒顶、片帮、底臌等破坏。
图4所示为巷道围岩变形破坏演化过程。图中:block state表示单元体的状态;none表示未破坏;shear-n表示现在处于剪切破坏状态;shear-p表示现在处于弹性状态,但过去处于剪切破坏状态;tension-n表示现在处于张拉破坏状态;tension-p表示现在处于弹性状态,但过去处于张拉破坏状态。由图4和图5可知:当应力释放率=5%时,巷道围岩未产生塑性区;当=35%时,在巷道底角处开始产生塑性区,其塑性区最大深度为0.5 m,塑性区总体积数(剪切破坏体积数)为24个;当=55%时,在巷道底板与顶板处产生了塑性区,顶底板塑性区最大深度为0.5 m,塑性区总体积数(剪切破坏体积数)为271个;当=60%时,在巷道底板、顶板及帮部均产生了塑性区,顶板与帮部塑性区最大深度为0.5 m,底板塑性区最大深度为1.0 m,塑性区总体积数(剪切破坏体积数)为936个;当=80%时,巷道围岩塑性区范围较大,顶板与帮部塑性区最大深度为1.5 m,底板塑性区最大深度为2.5 m,塑性区总体积数(剪切破坏体积数)为4 107个;当=100%时,巷道围岩塑性区范围更大,被挤压的围岩体将整个巷道空间充填,顶板与帮部塑性区最大深度为4.5 m,底板塑性区最大深度为5.0 m,塑性区总体积数为11 425个,拉伸破坏体积数为821个,剪切破坏体积数为10 604个。以上结果表明:随着应力释放率增加,巷道围岩塑性区范围与塑性区体积数呈非线性增大,并且围岩破坏以剪切破坏为主,拉伸破坏较少。
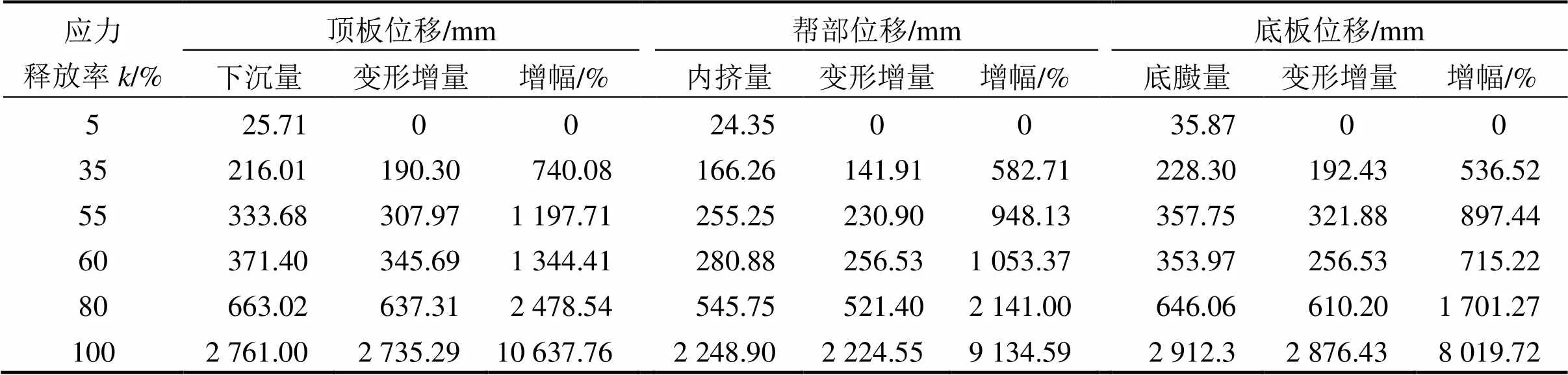
表2 不同应力释放率条件下巷道围岩位移量

应力释放率k/%:(a) 5;(b) 35;(c) 55;(d) 60;(d) 80;(f) 100

(a) 塑性区总体积;(b) 拉伸破坏区体积;(c) 剪切破坏区体积
在相同应力释放率条件下,随着岩性恶化,巷道围岩塑性区范围与塑性区体积数逐渐增加,并且产生围岩塑性区的应力释放率阈值随之降低。对于I类围岩,顶板与帮部塑性区最大深度为0.5 m,底板塑性区最大深度为1.0 m,塑性区总体积数(剪切破坏体积数)为1 034,产生围岩塑性区的应力释放率阈值d=85%;对于Ⅱ类围岩,顶板与帮部塑性区最大深度为0.5 m,底板塑性区最大深度为1.0 m,塑性区总体积数(剪切破坏体积数)为2 004,d=85%;对于Ⅲ类围岩,顶板、帮部及底板塑性区最大深度为1.5 m,塑性区总体积数(剪切破坏体积数)为2962,d=70%。对于Ⅳ类围岩,顶板与底板塑性区最大深度为3.5 m,帮部塑性区最大深度为3.0 m,塑性区总体积数为8 826个,拉伸破坏体积数为227个,剪切破坏体积数为8 599个,d=45%。对于Ⅴ类围岩,顶板与帮部塑性区最大深度为4.5 m,底板塑性区最大深度为5.0 m,塑性区总体积数为11 425,拉伸破坏体积数为821个,剪切破坏体积数最为10 604个,d=35%。以上结果表明:随着岩性的恶化,围岩体的抗拉或抗压强度不断降低,发生剪切或拉伸破坏的围岩体数量急剧增加,巷道围岩的稳定性随之降低。
2.2 不同埋深条件下巷道围岩变形与破坏特征分析
取围岩等级为Ⅴ类、巷道埋深为100,200,400,600,800,1 000,1 200和1 400 m共8种情况,计算时按5%的等级释放荷载,不同埋深条件下巷道围岩变形曲线如图6所示,不同埋深条件下巷道围岩塑性区分布如图7所示,不同埋深条件下巷道围岩塑性区体积曲线如图8所示;以应力释放率=60%为例,不同埋深条件下巷道围岩位移见表3。

(a) 顶板下沉量;(b) 帮部内挤量;(c) 底板底臌量
2.2.1 巷道围岩位移演化规律分析
由图6和表3可知:在巷道埋深条件下,随着应力释放率的增加,巷道围岩变形量随之增大,基本呈现出“底板底臌量>顶板下沉量>两帮内挤量”的演化规律。且在相同应力释放率条件下,随着巷道埋深的增加,巷道围岩变形量随之增大,围岩变形量与变形增量基本呈现出“底板底臌量>顶板下沉量>两帮内挤量”的演化规律,而围岩变形量增幅呈现出“顶板下沉量>两帮内挤量>底板底臌量”的演化规律。
2.2.2 巷道围岩变形破坏演化过程分析
由图7和图8可知:在相同应力释放率下,随着埋深增加,围岩塑性区范围与塑性区体积数逐渐增加,并且产生围岩塑性区的应力释放率阈值随之降低;当埋深=100 m时,顶板与帮部塑性区最大深度为1.5 m,底板塑性区最大深度为2.0 m,塑性区总体积数为4 487个,拉伸破坏体积数为110个,剪切破坏体积数为4 377个,产生围岩塑性区的应力释放率阈值d=50%;当埋深=200 m时,顶板与帮部塑性区最大深度为4.0 m,底板塑性区最大深度为4.5 m,塑性区总体积数为7 987个,拉伸破坏体积数为231个,剪切破坏体积数为7 756个,d=40%;当埋深=400 m时,顶板与帮部塑性区最大深度为4.0 m,底板塑性区最大深度为4.5 m,塑性区总体积数为8 924,拉伸破坏体积数为372个,剪切破坏体积数为8 553个,d=40%;当埋深=600 m时,顶板与底板塑性区最大深度为4.5 m,帮部塑性区最大深度为4.0 m,塑性区总体积数为9 842个,拉伸破坏体积数为494个,剪切破坏体积数为9 349个,d=35%。当埋深=800 m时,顶板与底板塑性区最大深度为5.0 m,帮部塑性区最大深度为4.5 m,塑性区总体积数为10 648个,拉伸破坏体积数为609个,剪切破坏体积数为10 039个,d=35%;当埋深=1 km时,顶板与帮部塑性区最大深度为4.5 m,底板塑性区最大深度为5.0 m,塑性区总体积数为11 425个,拉伸破坏体积数为821个,剪切破坏体积数为10 604个,d=35%;当埋深>1 km时,因巷道围岩变形过大造成计算中途终止。以上数据表明,随着巷道埋深的增加,发生剪切或拉伸破坏的围岩体数量急剧增加,巷道围岩的稳定性随之降低。

表3 不同埋深条件下巷道围岩位移

h/m:(a) 100;(b) 200;(c) 400;(d) 600;(d) 800;(f) 1 000

(a) 塑性区总体积;(b) 拉伸破坏区体积;(c) 剪切破坏区体积
2.3 基于应力释放率的合理注浆时机的确定
通过以上分析可知:对于深部软岩巷道而言,单一的支护形式难以维持围岩的基本稳定,常采用锚固与注浆组成的联合支护形式,为了充分发挥各支护体对围岩的控制效果,需确定合理的注浆时机,达到既充分释放存储于围岩内的变形能而降低支护强度,又充分利用围岩的自承力而降低支护成本的目的。巷道围岩的变形破坏过程是随开挖引起应力释放率的增大(或变形的增大)而不断渐进破坏的过程,并且在不同岩性与埋深(应力水平)条件下,巷道围岩塑性区范围与塑性区体积数随之变化,且产生围岩塑性区的应力释放率阈值不同。因此,可采用产生围岩塑性区的应力释放率阈值作为确定注浆时机的判据。
以安徽省淮南市安徽恒源煤电股份有限公司朱集西矿为例,从正反分析2方面说明“采用产生围岩塑性区的应力释放率阈值作为确定注浆时机的判据”的应用。朱集西矿大巷围岩位移与变形释放率曲线如图9所示。因井下大巷底臌量较大,每月需卧底1~2次,造成底板测点破坏而不得不多次布设,造成监测数据波动较大;而两帮测点较为固定,监测数据较为平稳。故为了准确地反映深部高应力软岩巷道围岩变形释放率,定义围岩两帮收敛变形量与其最大收敛变形量的比值为变形释放率(文中所指的围岩最大收敛变形量为通过井下监测获得的巷道围岩变形趋于稳定时的最大变形值,由于不同矿区的矿井地层条件与巷道所处的工程地质条件的差异,造成巷道围岩变形释放率是不同的,应区别使用)。为充分释放存储于巷道围岩内的变形能,在巷道开挖时将顶板与两帮各预留200 mm的变形量;通过文中深部高应力软岩巷道合理支护时机的理论分析,确定了注浆合理时机为围岩变形量达到150 mm,此时,围岩变形释放率为60%,其上限不超过巷道围岩预留变形量200 mm。

1—两帮移近量;2—顶底移近量;3—变形释放率。
同理,采用FLAC3D数值计算可得到巷道围岩变形和塑性区体积与应力释放率关系曲线,如图10所示。朱集西矿大巷围岩开始出现塑性区的应力释放率阈值d=40%,顶板与帮部围岩未产生塑性区,底板塑性区最大深度为0.5 m,塑性区总体积数(剪切破坏体积数)为61个;围岩顶板下沉量为109.81 mm,两帮内挤量为84.81 mm,底板底臌量为118.47 mm。大巷围岩周边均出现塑性区的应力释放率阈值d=60%,顶底板及两帮围岩塑性区最大深度为0.5 m,塑性区总体积数(剪切破坏体积数)为466个;围岩顶板下沉量为166.60 mm,两帮内挤量为126.32 mm,底板底臌量为176.56 mm。大巷围岩产生较大塑性区的应力释放率阈值d=80%,底板与帮部塑性区最大深度为1.5 m,顶板塑性区最大深度为1.0 m,塑性区总体积数(即剪切破坏体积数)为2 850个;围岩顶板下沉量为 275.66 mm,两帮内挤量为209.67 mm,底板底臌量为 252.67 mm。
分析以上数据可知:
1) 当应力释放率阈值k=40%时,巷道围岩刚开始产生塑性区,围岩基本处于变形破裂的发展阶段,围岩体裂隙开度较小,颗粒浆液难以注入,此时若进行注浆加固,则浆液难以注入、注浆效果较差,即注浆支护时机过早。当应力释放率阈值d=60%时,巷道周边塑性区均为分布,且数值较小(塑性区最大深度为0.5 m),未超过锚杆的长度(可控制围岩的范围),锚杆的锚固作用仍能发挥,可防止巷道冒顶与片帮;巷道围岩体存在相当开度的裂隙,浆液可注入,且破裂的围岩体仍具有一定的承载力而未失稳破坏,故此时注浆,可将破裂岩体重新胶结成再承载结构,与初次支护结构共同承载,可有效地控制围岩的大变形与损伤扩展,将围岩塑性区限制在锚杆加固范围内,保证巷道围岩与支护结构的长期稳定及安全。当应力释放率阈值d=80%时,巷道围岩产生了较大塑性区(塑性区最大深度为1.0~1.5 m),围岩体裂隙开度较大,浆液易注入;存储于围岩内的变形能大量释放,但两帮收敛变形量达到了209.67 mm,刚超过巷道围岩预留变形量200 mm的限值,此应力释放率阈值可作为注浆时机的上限。当应力释放率阈值d>80%时,巷道围岩塑性区更多,虽然存储于围岩内的变形能可得到充分释放,但巷道围岩变形破坏严重,已丧失了承载力,此时注浆已晚,即丧失了最佳的注浆时机。
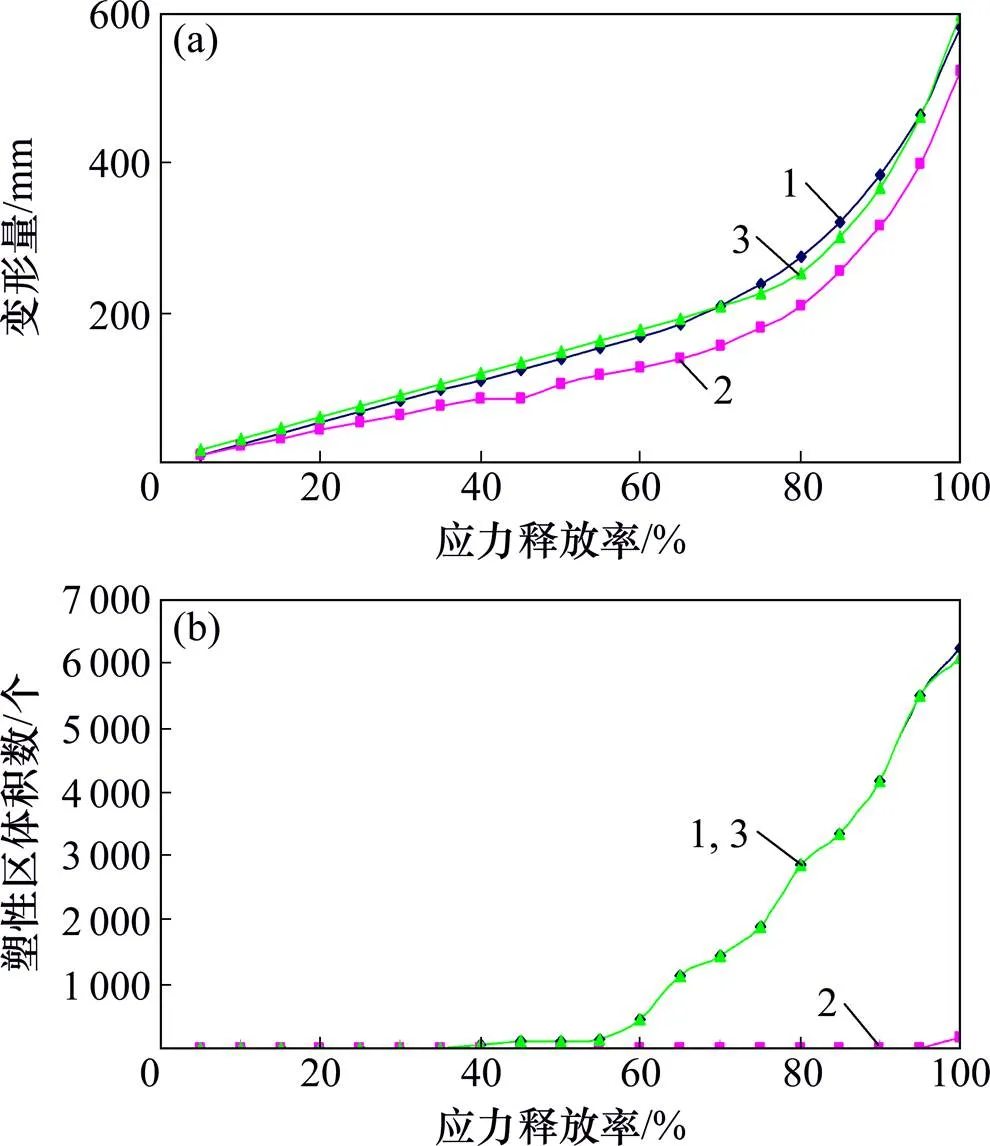
(a) 围岩变形量;(b) 塑性区总体积
2) 采用应力释放率阈值60%和围岩变形量 150 mm作为判定注浆时机的指标是合理的,两者可相互验证;并且应力释放率与变形释放率的作用是等同的,两者都可作为描述存储于围岩内变性能释放演化过程的指标。
3 深部高应力软岩巷道支护技术
3.1 深部高应力软岩巷道支护对策
在巷道掘进时,适当扩大掘进断面,即在巷道顶部和两帮各预留一定的变形量,以允许巷道围岩产生适量的变形,可使围岩中的高应力(变形能)得到释放,有利于降低应力集中程度,使围岩中高应力向更深部围岩转移,有利于降低支护强度。预应力锚杆支护既能实现围岩应力状态的恢复改善,又能有效地增强围岩[21];预应力锚索既能恢复改善围岩应力状态、增强围岩,又能实现承载圈的扩大[22];注浆既能实现应力的有效转移和应力峰值的减弱,又能有效地固结修复破裂围岩[23]。锚网喷初次支护后,围岩应力得到一定程度的释放,围岩的自承力有所提高;预应力锚索和全断面注浆补强加固起永久支护的作用,实现巷道围岩稳定的根本控制。通过注浆可将锚杆压缩拱、锚索深部承载圈形成内外圈承载结构有效地组合在一起,形成了高强度的多层锚壳组合拱结构,扩大了支护体系的承载范围,共同维持了深部高应力软岩巷道围岩与支护结构的长期稳定及安全。在巷道底板施工自钻式中空内注浆锚杆,一方面,通过锚杆加强底板支护,以增强底板岩体的抗剪能力,防止底板出现大的剪切滑移,造成巷道的整体失稳破坏;另一方面,通过注浆改善底板中部岩体的应力状态,提高底板岩层固有强度,抑制其拉伸破坏和隆起变形[24]。
考虑巷道围岩喷层承受的压力与注浆效果,采用低压浅孔充填注浆与高压深孔渗透注浆组成的分次耦合注浆技术。低压浅孔与高压深孔同管分次注浆,首先通过低压浅孔充填注浆,采用较小的注浆压力,保证喷层不破裂防止浆液溢出,将浅部围岩中的裂隙、缝隙充填起来,相当于形成1个较厚的止浆墙;再次采用较高的注浆压力,进行高压深孔注浆,将松动圈范围内的破碎围岩体都胶结起来,提高破裂围岩体的强度及稳定。
3.2 深部高应力软岩巷道支护技术方案与参数
在总结分析深部高应力软岩巷道支护对策的基础上,提出了深部高应力软岩巷道采用“锚网索喷+注浆+底板锚注”联合支护技术方案,并应用于工程实践,取得了良好的技术经济效益。
锚网喷索与型钢支架参数见表4,支护结构见 图11。
3.3 井下应用效果分析
为验证“锚网索喷+注浆+底板锚注”联合支护技术方案对巷道围岩控制效果及注浆时机选择的合理性,在西翼11煤矸石运输大巷进行了井下工业性试验,围岩变形监测曲线如图12所示。
由图12可知:西翼11煤矸石运输大巷顶板下沉量为3.84~6.66 mm,两帮内挤量为4.47~17.64 mm,底板底臌量为7.06~11.32 mm。这表明采用的“锚网索喷+注浆+底板锚注”联合支护技术方案,可有效地控制深部高应力软岩巷道的大变形与底臌,保证了巷道围岩与支护结构的长期稳定及安全,验证了所确定的注浆时机是合理、可行的。
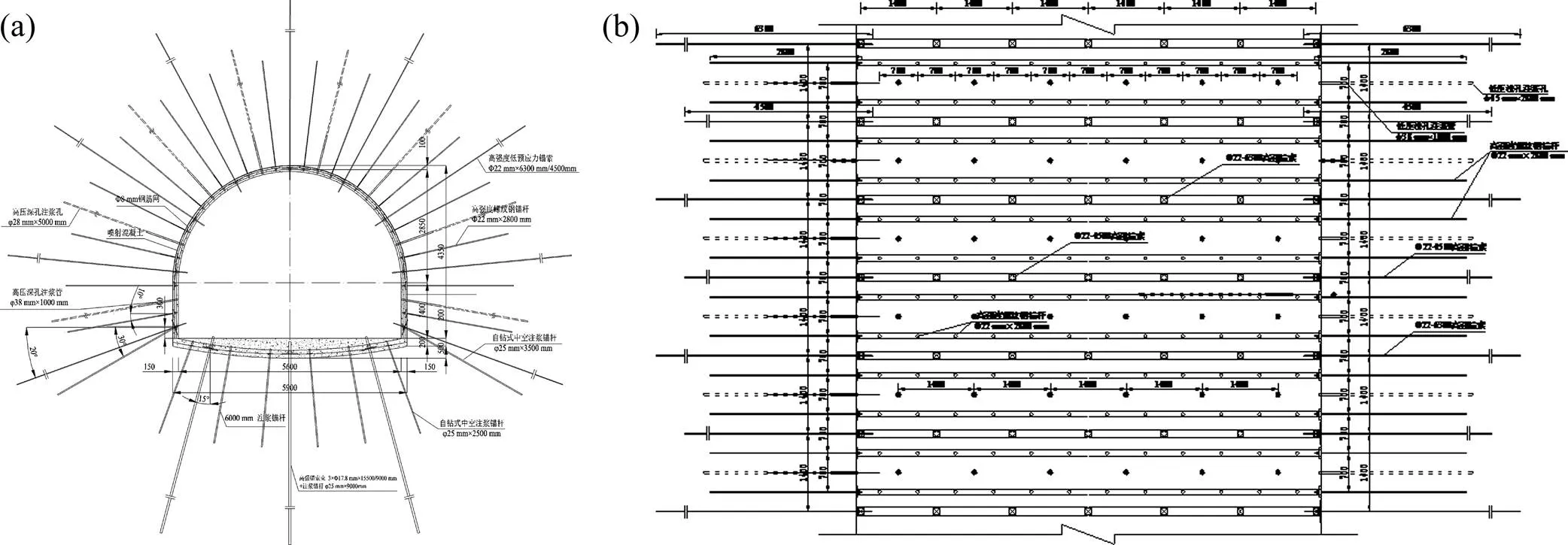
(a) 支护断面图;(b) 支护俯视图

表4 深部高应力软岩巷道支护形式及规格参数
注:巷道顶板与两帮各预留200 mm的变形量。
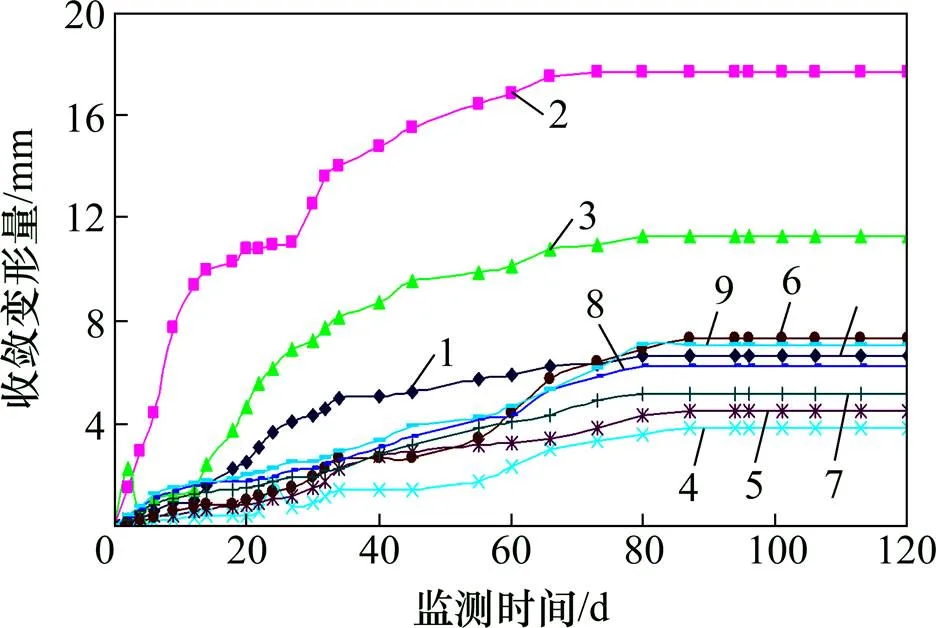
1—1号监测断面顶板下沉量;2—1号监测断面两帮内挤量;3—1号监测断面底板底臌量;4—2号监测断面顶板下沉量;5—2号监测断面两帮内挤量;6—2号监测断面底板底臌量;7—3号监测断面顶板下沉量;8—3号监测断面两帮内挤量;9—3号监测断面底板底臌量。
4 结论
1) 基于弹塑性理论分析,揭示了朱集西煤矿深部高应力软岩巷道围岩收敛变形与支护强度及围岩自承力的变化关系,获得了巷道围岩位移与支护强度的关系曲线。巷道围岩的适当变形可释放存储于围岩内的变形能,所需的支护强度显著降低;当围岩变形量过大时,巷道围岩松散破碎,自承力减低,所需的支护强度反而增加。当变形量为150 mm左右时,实现了充分释放存储于围岩内的变形能而降低支护强度及利用围岩的自承力而降低支护成本的目的。
2) 在同一岩性条件下,随着应力释放率增加,巷道围岩变形量随之增大,围岩变形量与变形增量基本呈现出“底板底臌量>顶板下沉量>两帮内挤量”的演化规律。随着岩性恶化,巷道围岩变形量与变形增量随之增大,巷道围岩塑性区范围与塑性区体积数逐渐增加,且产生围岩塑性区的应力释放率阈值随之降低。
3) 在巷道埋深条件下,随着应力释放率增加,巷道围岩变形量随之增大,基本呈现出“底板底臌量>顶板下沉量>两帮内挤量”的演化规律;在相同应力释放率条件下,随着巷道埋深的增加,巷道围岩变形量随之增大,巷道围岩塑性区范围与塑性区体积数逐渐增加,且产生围岩塑性区的应力释放率阈值随之 降低。
4) 采用应力释放率阈值60%和围岩变形量150 mm,作为判定注浆时机的指标是合理的,两者可相互验证;并且应力释放率与变形释放率的作用是等同的,两者都可作为描述存储于围岩内变性能释放演化过程的指标。工程实践表明,“锚网索喷+注浆+底板锚注”联合支护技术方案有效地解决了深部高应力软岩巷道支护难题,验证了所确定的注浆时机是合理、可行的。
[1] 何满潮. 深部软岩工程的研究进展与挑战[J]. 煤炭学报, 2014, 39(8): 1409−1417. HE Manchao. Progress and challenges of soft rock engineering in depth[J]. Journal of China Coal Society, 2005, 2014, 39(8): 1409−1417.
[2] 谢和平, 高峰, 鞠杨. 深部岩体力学研究与探索[J]. 岩石力学与工程学报, 2015, 34(11): 2161−2178. XIE Heping, GAO Feng, JU Yang. Research and development of rock mechanics in deep ground engineering[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(11): 2161−2178.
[3] 王琦, 李为腾, 李术才, 等. 深部巷道U型约束混凝土拱架力学性能及支护体系现场试验研究[J]. 中南大学学报(自然科学版), 2015, 46(6): 2250−2260. WANG Qi, LI Weiteng, LI Shucai, et al. Field test study on mechanical properties of U-type confined concrete arch centering and support system in deep roadway[J]. Journal of Central South University (Science and Technology), 2015, 46(6): 2250−2260.
[4] 刘泉声, 高玮, 袁亮. 煤矿深部岩巷稳定控制理论与支护技术及应用[M]. 北京: 科学出版社, 2010: 183−192. LIU Quansheng, GAO Wei, YUAN Liang. Theory and supporting technology of deep mine rock in stability controlling and its application[M]. Beijing: Science Press, 2010: 183−192.
[5] 牛双建, 靖洪文, 张忠宇, 等. 深部软岩巷道围岩稳定控制技术研究及应用[J]. 煤炭学报, 2011, 36 (6): 914−919. NIU Shuangjian, JING Hongwen, ZHANG Zhongyu, et al. Study on control technology of surrounding rocks in deep soft roadway and its application[J]. Journal of China Coal Society, 2011, 36(6): 914−919.
[6] 康红普, 王金华, 林健. 煤矿巷道锚杆支护应用实例分析[J]. 岩石力学与工程学报, 2010, 29(4): 649−664. KANG Hongpu, WANG Jinhua, LIN Jian. Case studies of rock bolting in coal mine roadways[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(4): 649−664.
[7] 孟庆彬, 韩立军, 乔卫国, 等. 赵楼矿深部软岩巷道变形破坏机理及控制技术[J]. 采矿与安全工程学报, 2013, 30(2): 165−172. MENG Qingbin, HAN Lijun, QIAO Weiguo, et al. The deformation failure mechanism and control techniques of soft rock in deep roadways in Zhaolou Mine[J]. Journal of Mining & Safety Engineering, 2013, 30(2): 165−172.
[8] 何满潮, 孙晓明. 中国煤矿软岩巷道工程支护设计与施工指南[M]. 北京: 科学出版社, 2004: 35−42. HE Manchao, SUN Xiaoming. Guide for design and construction of supporting design and construction for soft rock roadway in china[M]. Beijing: Science Press, 2004: 35−42.
[9] 来颖, 肖明, 胡田清. 地下洞室开挖锚固支护时机数值模拟[J]. 水电能源科学, 2011, 29(1): 89−92. LAI Ying, XIAO Ming, HU Tianqing. Numerical simulation of anchorage supporting opportunity for excavation of underground chamber[J]. Water Resources and Power, 2011, 29(1): 89−92.
[10] 李晓红. 隧道新奥法及其量测技术[M]. 北京: 科学出版社, 2002: 1−4. LI Xiaohong. New austrian tunnelling method and its measurement technology[M]. Beijing: Science Press, 2002: 1−4.
[11] 陆银龙, 王连国, 张蓓, 等. 软岩巷道锚注支护时机优化研究[J]. 岩土力学, 2012, 33(5): 1395−1401. LU Yinlong, WANG Lianguo, ZHANG Bei, et al. Optimization of bolt-grouting time for soft rock roadway[J]. Rock and Soil Mechanics, 2012, 33(5): 1395−1401.
[12] 王小平. 软岩巷道合理支护时间模拟研究[J]. 采矿与安全工程学报, 2006, 23(1): 103−106. WANG Xiaoping. Time simulation of rational support for soft rock roadway[J]. Journal of Mining & Safety Engineering, 2006, 23(1): 103−106.
[13] 孙晓明, 杨军, 曹伍富. 深部回采巷道锚网索耦合支护时空作用规律研究[J]. 岩石力学与工程学报, 2007, 26(5): 895−900. SUN Xiaoming, YANG Jun, CAO Wufu. Research on space-time action rule of bolt-net-anchor coupling support for deep gateway[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(5): 895−900.
[14] 王祥秋, 杨林德, 高文华. 软弱围岩蠕变损伤机理及合理支护时间的反演分析[J]. 岩石力学与工程学报, 2004, 23(5): 793−796. WANG Xiangqiu, YANG Linde, GAO Wenhua. Creep damage mechanism and back analysis of optimum support time for soften rockmass[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(5): 793−796.
[15] 屈延嗣, 罗立强, 王卫军, 等. 曲江煤矿深部岩巷破坏机理及锚索合理支护时间的确定[J]. 湖南科技大学学报(自然科学版), 2014, 29(2): 14−17. QU Yansi, LUO Liqiang, WANG Weijun, et al. Failure mechanism and timing of anchor support for deep rock roadway on qujiang mine[J]. Journal of Hunan University of Science & Technology (Natural Science Edition), 2014, 29(2): 14−17.
[16] 靖洪文, 李元海, 赵保太, 等. 软岩工程支护理论与技术[M]. 徐州: 中国矿业大学出版社, 2008: 178−184. JING Hongwen, LI Yuanhai, ZHAO Baotai, et al. Theory and technology of soft rock engineering support[M]. Xuzhou: China University of Mining and Technology Press, 2008: 178−184.
[17] HOEK E. Strength of rock and rock masses[J]. ISRM News Journal, 1994, 2(2): 4−16.
[18] 范加冬. 深部软岩巷道耦合机制及参数优化研究[D]. 徐州: 中国矿业大学力学与建筑工程学院, 2014: 26−29. FAN Jiadong. Study on the mechanism of coupling support technology and the parameter optimization in deep soft roadway[D]. Xuzhou: China University of Mining & Technology. School of Mechanics and Civil Engineering, 2014: 26−29.
[19] 郑颖人, 朱合华, 方正昌, 等. 地下工程围岩稳定分析与设计理论[M]. 北京: 人民交通出版社, 2012: 32−43. ZHENG Yingren, ZHU Hehua, FANG Zhengchang, et al. Stability analysis and design theory for surrounding rock of underground engineering[M]. Beijing: People’s Transportation Press, 2012: 32−43.
[20] 贺永年, 韩立军, 王衍森. 岩石力学简明教程[M]. 徐州: 中国矿业大学出版社, 2010: 145−152. HE Yongnian, HAN Lijun, WANG Yansen. Simple tutorial on rock mechanics[M]. Xuzhou: China University of Mining and Technology Press, 2010: 145−152.
[21] 薛顺勋. 软岩巷道支护技术指南[M]. 北京: 煤炭工业出版社, 2001: 19−23. XUE Shunxun. Soft rock roadway support technology guide[M]. Beijing: Coal Industry Press, 2001: 19−23.
[22] 刘红岗, 贺永年, 韩立军, 等. 大松动圈围岩锚注与预应力锚索联合支护技术的机理与实践[J]. 中国矿业, 2007, 16(1): 62−65. LIU Honggang, HE Yongnian, HAN Lijun, et al. Study and application of supportingmechanism of combined support of bolting2grouting and prestressed cable anchor in large broken zone surrounding rock[J]. China Miningmagazine, 2007, 16(1): 62−65.
[23] 李明远, 王连国, 易恭猷, 等. 软岩巷道锚注支护理论与实践[M]. 北京: 煤炭工业出版社, 2001: 24−39.LI Mingyuan, WANG Lianguo, YI Gongyou, et al. The theory and practice of anchor injection support for soft rock roadway[M]. Beijing: Coal Industry Press, 2001: 24−39.
[24] 刘泉声, 肖虎, 卢兴利, 等. 高地应力破碎软岩巷道底臌特性及综合控制对策研究[J]. 岩土力学, 2012, 33(6): 1703−1710.LIU Quansheng, XIAO Hu, LU Xingli, et al. Research on floor heave characteristics of broken soft rocks with high geostress and its comprehensive control measures[J]. Rock and Soil Mechanics, 2012, 33(6): 1703−1710.
(编辑 杨幼平)
Optimization analysis of grouting timing in deep and high stress soft rock roadway
MENG Qingbin1, HAN Lijun1, WANG Qi2, ZHANG Jian1, FAN Jiadong1, NIE Junwei1, WEN Shengyong1
(1. State Key Laboratory for Geomechanics and Deep Underground Engineering,China University of Mining and Technology, Xuzhou 221116, China;2. Research Center of Geotechnical and Structural Engineering, Shandong University, Jinan 250061, China)
The relationship between convergence deformation, supporting strength and bearing capacity of surrounding rock in deep high stress soft rock roadway of Zhujixi Coal Mine was revealed. The curves of displacement of surrounding rock and the supporting strength were obtained. Using Fish language embedded in FLAC3Dto programme the volume numbers of plastic zone, tensile failure zone and shear failure zone of roadway were extracted. The evolution law of surrounding rock deformation and plastic zone expansion along the stress release rate with different lithology and buried depth was revealed. The evolution process from local failure to whole instability failure of the surrounding rock was produced. The stress release rate threshold value was adopted as an indicator for determining grouting time. Based on the theoretical analysis, numerical calculation and analysis of measured data of surrounding rock deformation were made.The results show that when the displacement of surrounding rock is 150 mm, the deformation energy stored in the surrounding rock will be fully released. Besides, self-bearing capacity of surrounding rock is utilized to the maximum utilization. It is reasonable to use the stress release rate threshold 60% and surrounding rock deformation with 150 mm as the index of judging the grouting timing. Both of them could be mutually verified. The scheme of combined supporting technology for bolting and shotcreting+grouting+floor bolt-grouting is put forward and it solves the supporting problem in deep high stress soft rock roadway. In addition, the reasonable and feasible grouting time is verified.
deep high stress; soft rock roadway; grouting timing; stress release rate; surrounding rock−supporting characteristic curves
10.11817/j.issn.1672−7207.2017.10.029
TD325.4
A
1672−7207(2017)10−2765−12
2016−11−10;
修回日期:2017−03−10
国家自然科学基金资助项目(51704280,51579239,51574223);中国博士后科学基金资助项目(2015M580493,2017T100420),山东省土木工程防灾减灾重点实验室开放课题(CDPM2014KF03)(Projects (51704280, 51579239, 51574223) supported by the National Natural Science Foundation of China; Projects (2015M580493, 2017T100420) supported by China Postdoctoral Science Foundation; Project(CDPM2014KF03)supported by Shandong Provincial Key Laboratory of Depositional Mineralization & Sedimentary Minerals (Shangdong University of Science and Technology)
孟庆彬,博士,助理研究员,从事岩体加固理论与应用技术研究;E-mail:mqb1985@126.com

