感应加热工艺参数对Q345钢弯曲角度和曲率半径的影响
张继祥,周 伟,徐 昱,钟 厉,2
(1.重庆交通大学 机电与汽车工程学院,重庆 400074; 2.重庆交通大学 重庆市特种船舶数字化设计与制造工程技术研究中心,重庆 400074)
感应加热工艺参数对Q345钢弯曲角度和曲率半径的影响
张继祥1,2,周 伟1,徐 昱1,钟 厉1,2
(1.重庆交通大学 机电与汽车工程学院,重庆 400074; 2.重庆交通大学 重庆市特种船舶数字化设计与制造工程技术研究中心,重庆 400074)
基于ANSYS有限元分析软件,采用APDL语言实现高频感应加热成形中电-磁-热-力等多物理场耦合,建立了高频感应加热弯板的三维移动式有限元模型,并系统研究了高频感应加热弯板成形目标与工艺参数的关系。结果表明:加热功率较大时,钢板弯曲角度随着热源移动速度增加先增大再减小,而加热功率较小时钢板弯曲角度随着热源移动速度增加直线下降;钢板弯曲曲率半径随热源移动速度增加而增大,随加热功率增大而减小。最后分别建立了弯曲角度、曲率半径与加热功率和热源移动速度的函数关系式。
船舶工程;有限元模拟;高频感应;弯板成形;函数关系
水火弯板成形在船板制造领域效率低,形状达不到要求,而高频感应加热弯板成形具有温度控制精准、氧化少、污染少、加热效率极高、工作环境清洁安全、有利于实现自动化加工等优势[1-3],已成为一种广泛应用的板材热应力成形方法,国内外相关学者均在开展这方面的研究。
在国外,K.Y.BAE等[4]运用统计方法对感应加热变形与加热参数之间的关系进行了研究,并证实了其方程的合理性;J.H.LEE等[5]建立有限元模型,分析了钢板高频感应加热和可燃气体加热下钢板的残余应力和变形;C.D.JANG等[6]则提出了钢板变形预测可通过仿真模拟技术来实现的思想。
在国内,相关学者也开展了相关的研究,并取得了许多成果。殷筱依等[7]、刘芳平等[8]研究了薄壁件的翘曲和屈曲;范平等[9]、张继祥等[10]和安国银等[11]分别建立了静止的电、磁、热耦合热源模型,但所建立的感应热源是通过温度场与磁场间接耦合得到,该模型只能实现二维静止加热模拟,无法移动;张雪彪等[12-13]建立了三维静止式磁热耦合热源模型,实现了三维静态的耦合模拟,但没有进行移动加热模拟;周宏等[14]、张继祥等[15-16]和徐昱[17]分别进行了三维移动式有限元模型的研究。
笔者在相关学者提出的电-磁-热-力等多物理场耦合实现方法的基础上[15-16],基于ANSYS二次开发APDL语言,建立了三维移动式的高频感应加热弯板有限元模型;系统研究了成形工艺参数对钢板弯曲角度、曲率半径等的影响;并建立成型参数与成形目标之间的关系模型。
1 有限元建模
1.1 限元模型
模拟实验采用400 mm×200 mm×10 mm船用钢板,材质为Q345。实际圆形感应线圈是使用直径6 mm、壁厚1 mm的铜管缠绕而成。为简化有限元建模模型,将圆形线圈改为34 mm×34 mm×6 mm面积相等的矩形线圈,线圈与钢板间距2 mm,且截面电流加载方向和圆形线圈的方向一致。图1为高频感应成形实的有限元模型。
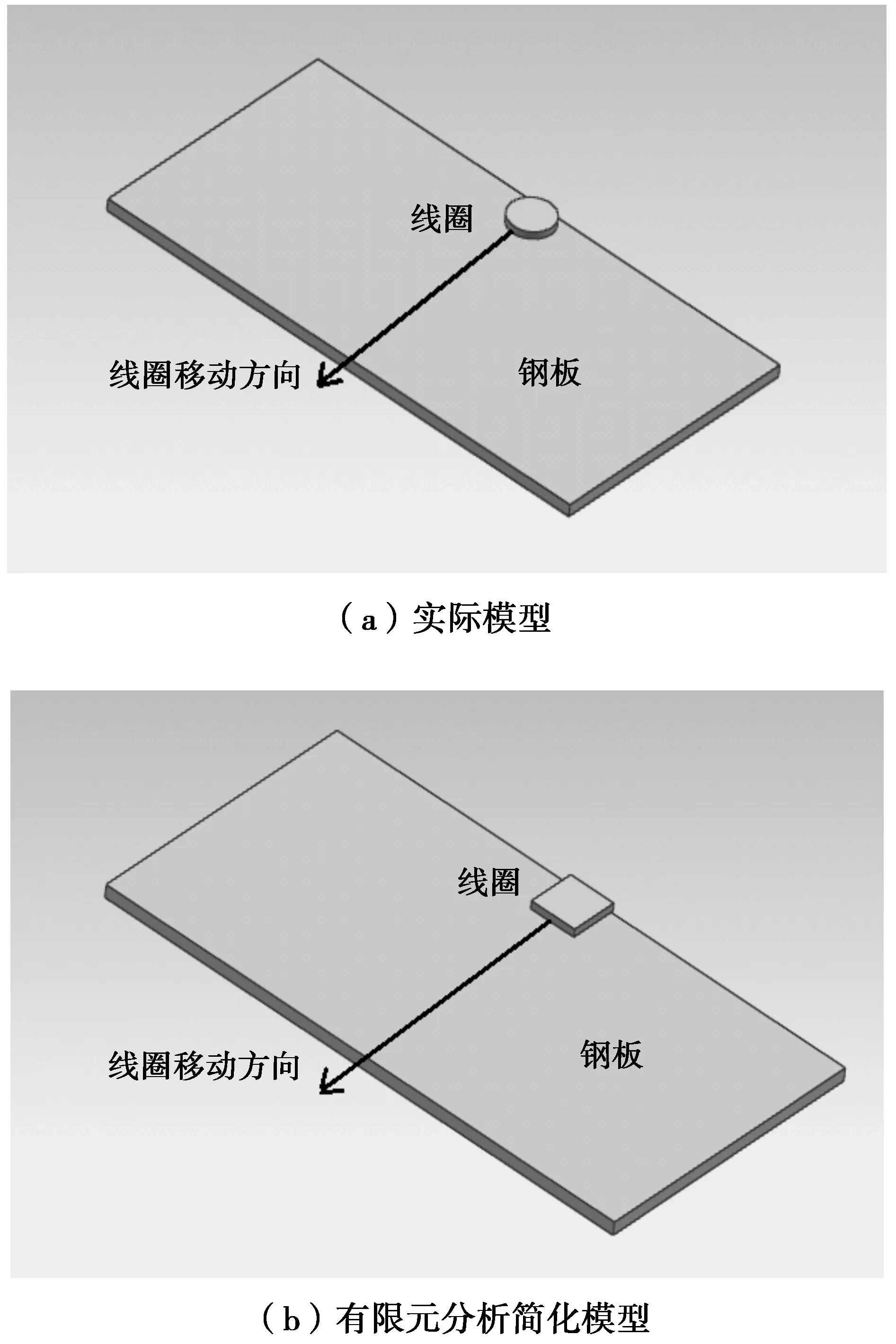
图1 钢板高频感应加热成形模型Fig.1 High frequency induction heating formation model of steel plate
1.2 网格划分
在计算谐波磁场时,采用SOLID97磁矢量单元,温度场分析时采用8节点SOLID70热实体单元,在进行结构应力场计算时采用SOLID185单元等效替换SOLID70单元。划分后的模型如图2。
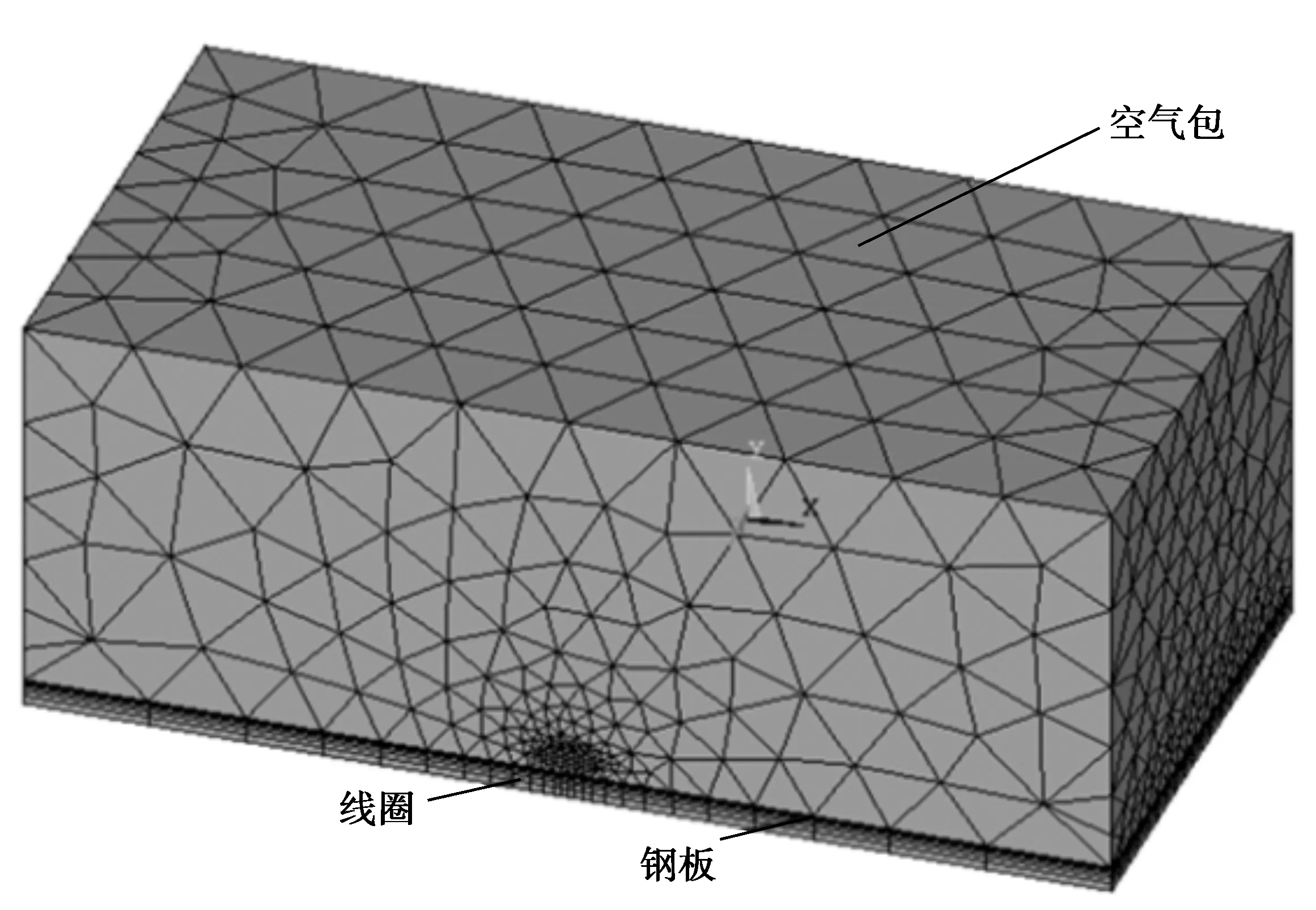
图2 有限元网格划分Fig.2 Finite element meshing
1.3 模拟计算流程
笔者基于ANSYS软件,耦合温度场和磁场热源,使用APDL语言循环语句来完成对热源的移动,并对移动式三维感应加热电磁-热-应力多物理场进行模拟,耦合模拟计算流程如图3。
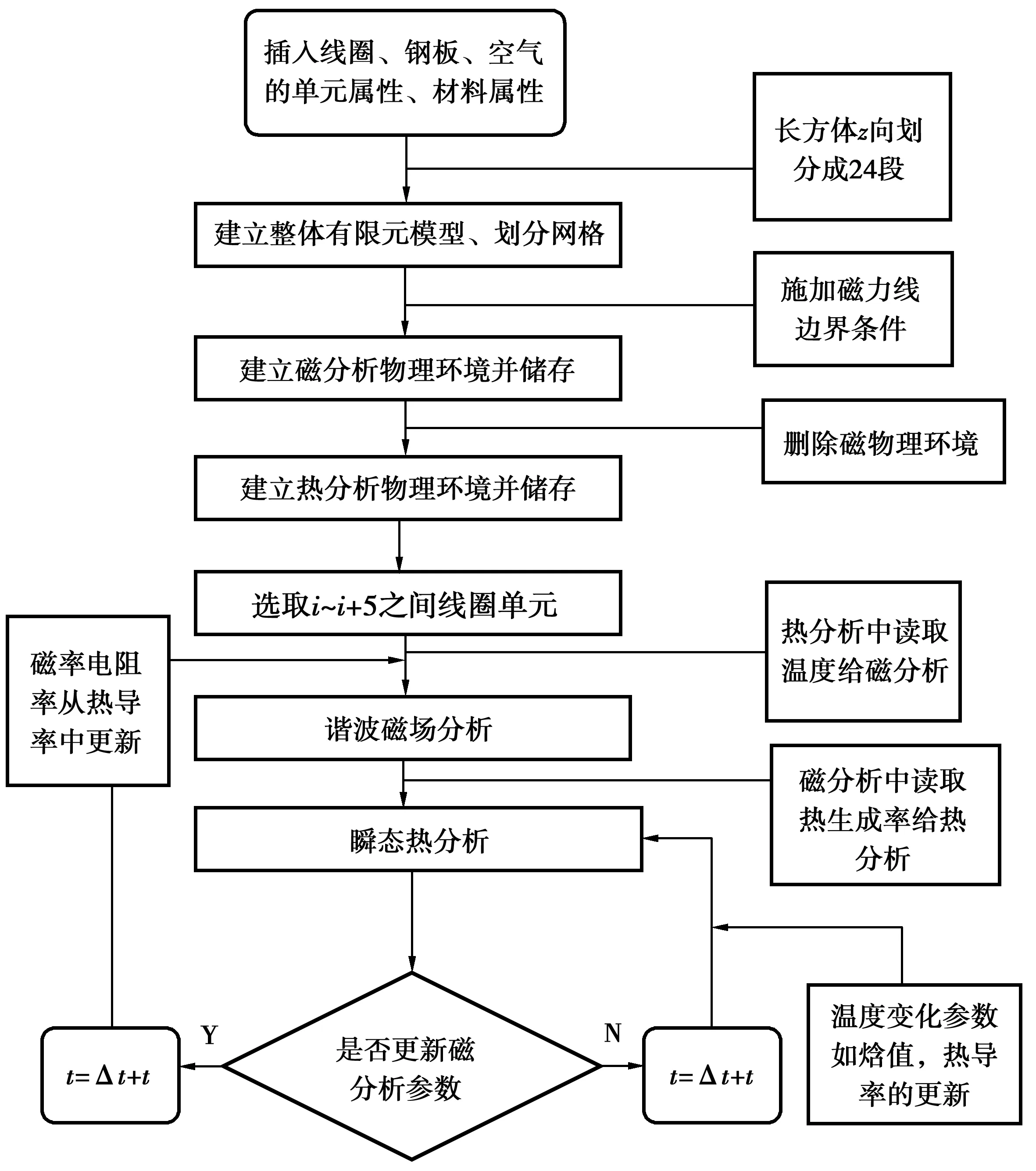
图3 模型编程算法流程Fig.3 Algorithm flow chart of model programming
1.4 边界及约束条件(图4)
如图4,在钢板左右两侧面和底部两端交线上的所有点施加UY=0 约束。为更加准确的模拟出实际状况下磁力线情况,对所有边界上的点施加磁力约束。在Z轴方向上,为了模拟X-Y平面上的磁场,对Z=0和Z=M的平面上分别施加与其平行的AZ=0约束;为了模拟X平面上的磁场,在X=-L和X=L的平面上,分别施加与其平行的AZ=0约束。
散热边界条件。在钢板上下、前后表面以及右侧面分别施加换热系数为15、10 W/(m2·℃)的散热边界条件[13]。
1.5 材料参数
Q345钢热物理参数中导热系数K、屈服强度σs、切变模量G、弹性模量E、磁导率μ等参数[14]如表1,假定铜线圈和空气的磁导率μ=1 H/m。
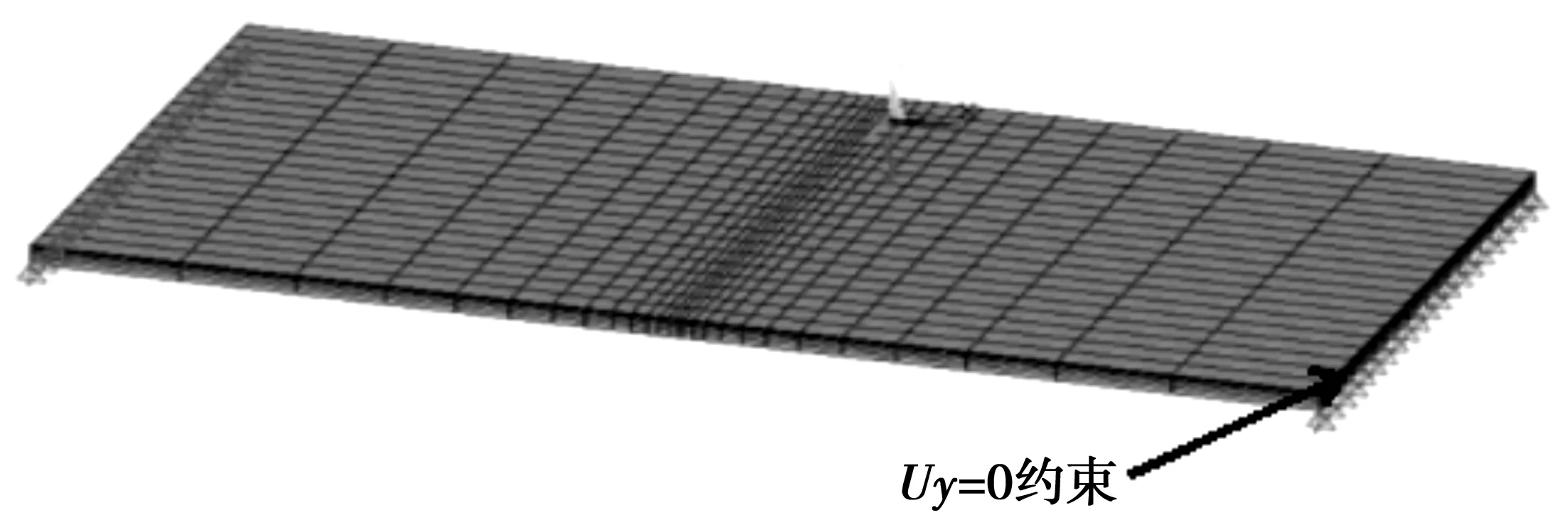
图4 模型约束条件Fig.4 Model constraints
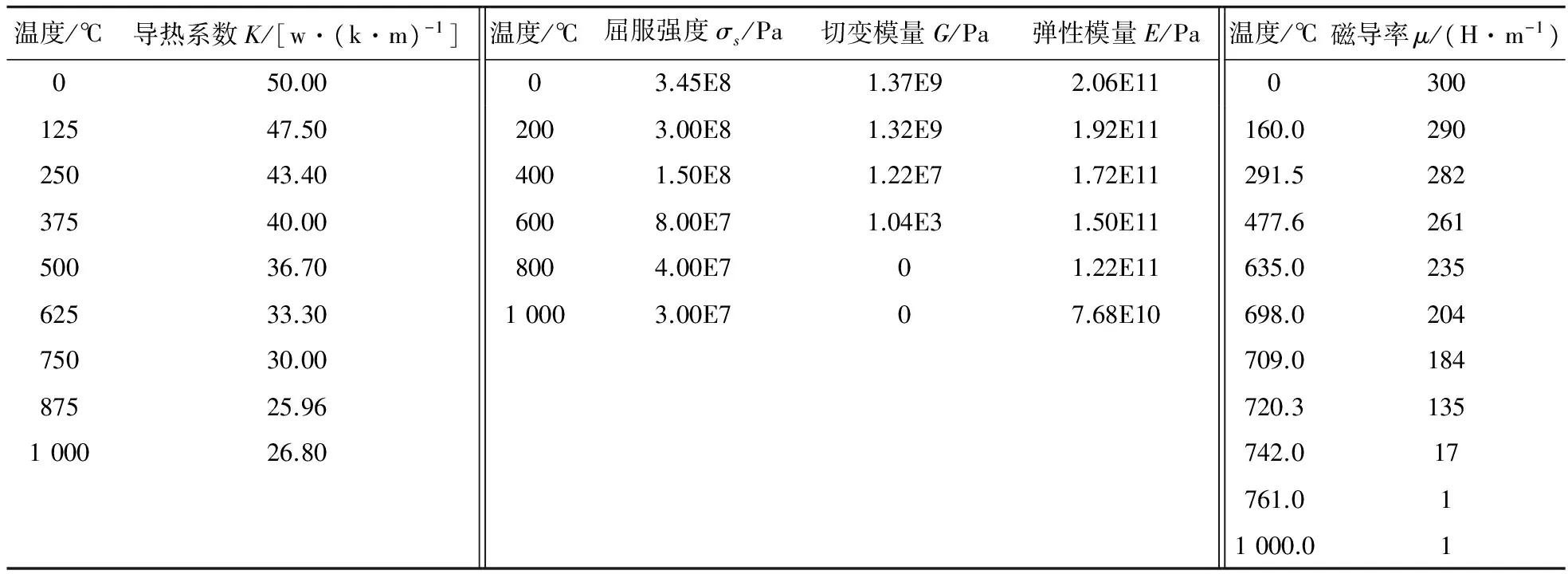
温度/℃导热系数K/[w·(k·m)-1]温度/℃屈服强度σs/Pa切变模量G/Pa弹性模量E/Pa温度/℃磁导率μ/(H·m-1)050.0003.45E81.37E92.06E11030012547.502003.00E81.32E91.92E11160.029025043.404001.50E81.22E71.72E11291.528237540.006008.00E71.04E31.50E11477.626150036.708004.00E701.22E11635.023562533.3010003.00E707.68E10698.020475030.00709.018487525.96720.3135100026.80742.017761.011000.01
1.6 研究方案
电源频率为20 kHz,设定的功率分别为20、25、30、35 kW,采用10~30 mm/s 的移动速度对弯板工艺进行了数值模拟。
2 数值模拟结果及分析
2.1 工艺参数对弯曲角度影响(图5)
由图5可看出:加热功率较大时(25~35 kW),钢板弯曲角度随着热源移动速度增加先增大再减小;加热功率较小时(20 kW),钢板弯曲角度随着热源移动速度增加直线下降,没有出现峰值;不同功率下弯曲角度峰值出现位置不同,功率越大,峰值对应的加热速度越大。
热源移动速度较小时,加热功率对弯曲角度影响不大,但随着热源移动速度的增加,功率对弯曲角度的影响变大,功率越大,成形角度越大。热源的移动速度较小时,钢板的透热性较好,厚度方向上温度梯度变化小,热应力都较小,所以弯曲角度在各功率下变化不大;随着热源移动速度不断增加。加热功率较低时,钢板透热性变差,厚度方向上温度梯度变化较大;热应力增加,钢板的弯曲应力也随之增加,但钢板底部的温度较低,强度较大,底部材料不能够发生塑形拉伸。所以在低功率加热时,弯曲角度随着热源移动速度的增加而减小。
随着热源移动速度的不断增加,在加热功率较高时,钢板透热性变好,厚度方向上温度梯度较小,热应力增加,钢板总的弯曲应力也随之增加,此时底部钢板温度较高,屈服应力较低,发生了塑性伸长变形,所以弯曲角度不断增加。由于线能量的原因,钢板底部加热温度随热源移动速度的增加而不断降低,在弯曲应力与塑形变形抗力的综合作用下,弯曲角度会达到一个峰值,然后逐渐下降。
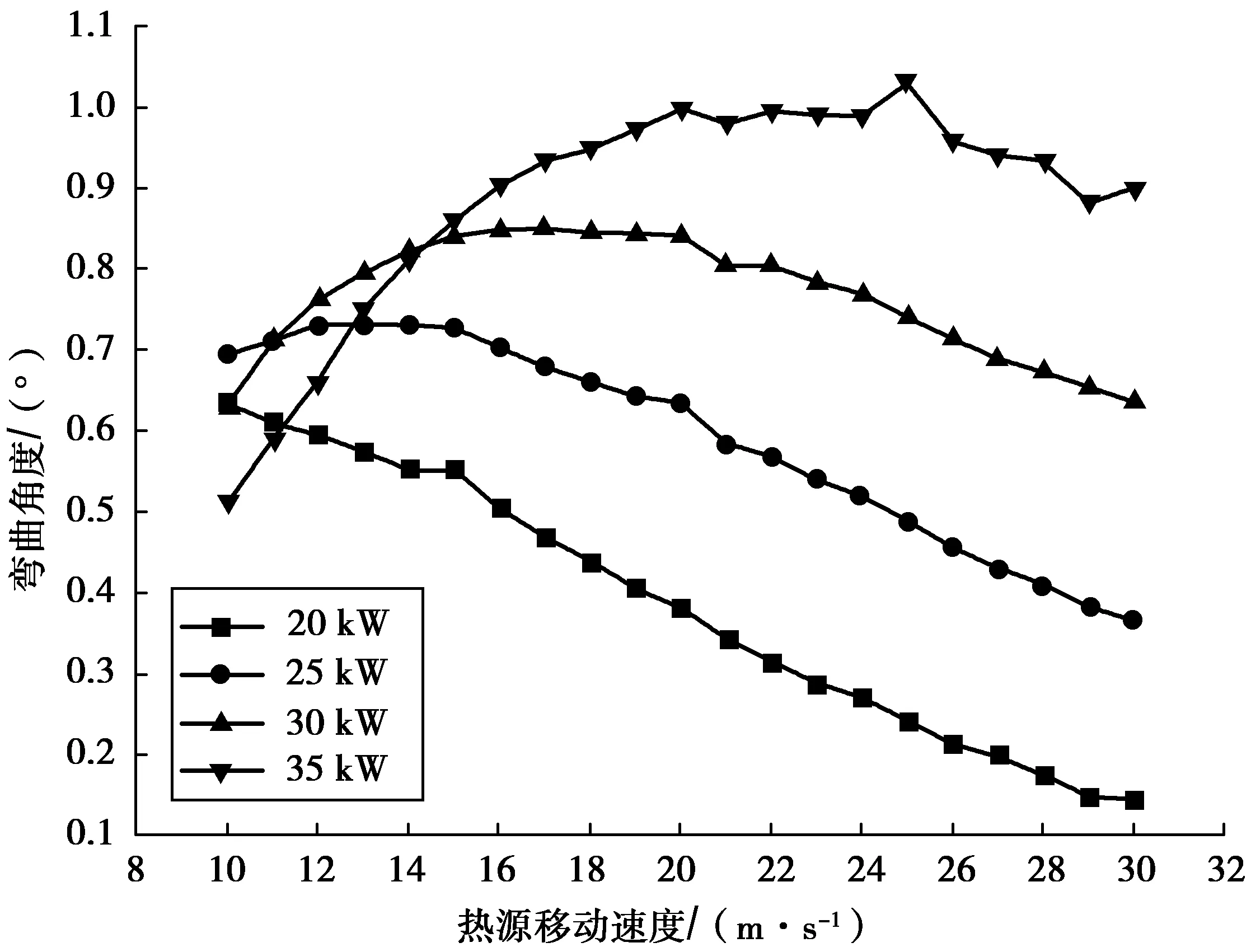
图5 弯曲角度与热源移动速度关系Fig.5 Relationship between bending angle and heat source moving speed
2.2 工艺参数对曲率半径影响(图6)
由图6可看出:钢板弯曲曲率半径随着热源移动速度增加而不断增大;加热功率越大,上升幅度越小,即加热功率越大曲率半径越小。
在热源的移动速度较小时,钢板的透热性较好,厚度方向上温度梯度变化小,热应力都较小,所以弯曲角度在各功率下变化不大。各功率下钢板的弯曲曲率半径都随热源移动速度的增加而不断增大,同一热源移动速度下功率越大钢板弯曲曲率半径越小。这是因为钢板的弯曲曲率半径是由弯曲部分的弧线和弯曲角度共同决定的。在热源移动速度相同,弧长一定时,功率越小使得钢板弯曲角度越小,钢板曲率半径则越大;当加热功率一定时,钢板弯曲角度随热源移动速度增大而越小,钢板的曲率则半径越大。
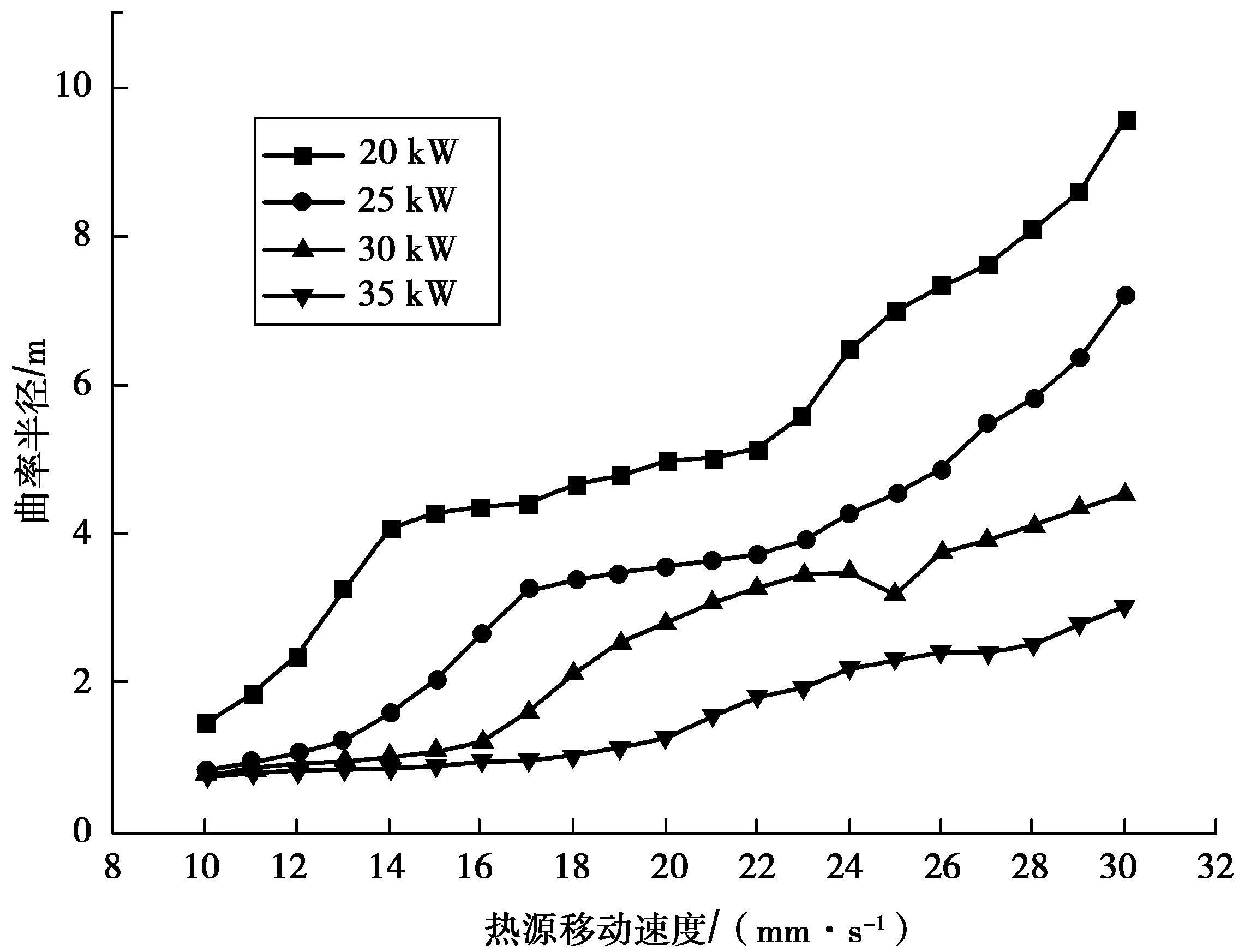
图6 曲率半径与热源移动速度关系Fig.6 Relationship between curvature radius and heat source moving speed
2.3 弯曲角度与热源移动速度、加热功率关系
弯曲角度与热源移动速度、加热功率之间的函数关系如式(1):
θ=f(x,y)=f(v,P)
(1)
式中:θ为目标值弯曲角度,(°);v为热源移动速度,mm/s;P为加热功率,kW。
笔者建立上述函数关系如式(1),并采用MATLAB曲面拟合功能进行3次多项式函数拟合,拟合结果如图7。
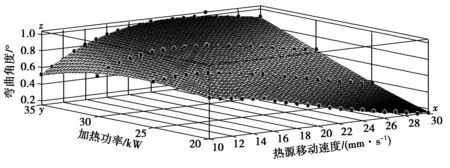
图7 弯曲角度-加热功率-热源移动速度拟合曲面Fig.7 Bending angle-heating power-heat source moving speed fitting surface
图7中,x轴表示热源移动速度,mm/s;y轴表示加热功率,kW;z轴表示钢板冷却后的弯曲角度,(°)。曲面顶点位置即最大弯曲角度以及对应的源移动速度、加热功率工艺参数值。
在热源移动速度为v=22 mm/s、加热功率为P=35 kW的热加工参数下,钢板得到最大弯曲角度。运用MATLAB软件拟合结果得到的弯曲角度与热源移动速度、加热功率的函数关系如式(2):
f(v,P)=p00+p10v+p01P+p20v2+p11vP+p02P2+p30v3+p21v2P+p12vP2+p03P3
(2)
式中:p00=0.344 9,p10=-0.045 57,p-01=0.030 59,p20=0,p11=0.003 26,p02=-0.898 6×10-3,p30=9.306×10-5,p21=0,p12=0.139 7×10-3,p03=-3.378×10-5。
上述拟合的置信度为95%,方差为0.009 236。
2.4 曲率半径与热源移动速度、加热功率关系
函数曲率半径与热源移动速度、加热功率之间的关系函数如式(3):
R=g(x,y)=g(v,P)
(3)
式中:R为目标值曲率半径,m。
笔者建立上述函数关系如式(3),采用MATLAB曲面拟合功能进行3次多项式函数拟合,拟合结果如图8。
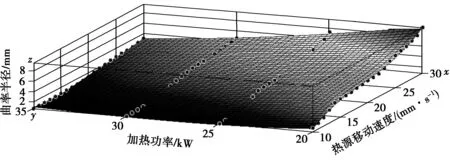
图8 曲率半径-加热功率-热源移动速度拟合曲面Fig.8 Curvature radius-heating power-heat source moving speed fitting surface
由图8可知:x轴表示热源移动速度,mm/s;y轴表示加热功率,kW;z轴表示钢板冷却后的弯曲曲率半径,m。
经MATLAB拟合处理结果得到的曲率半径与热源移动速度、加热功率的函数关系如式(4):
g(v,P)=p00+p10v+p01P+p20v2+p11vP+p02P2+p30v3+p21v2P+p12vP2+p03P3+p40v4+p31v3P+p22v2P2+p13vP3+p50v5+p41v4P+p32v3P2+p23v2P3
(4)
式中:p00=-146.4,p10=26.7,p01=11.88,p20=-1.193,p11=-2.129,p02=-0.319 1,p30=0.014 97,p21=0.092 06,p12=0.052 5,p03=0.003 385,p40=0.000 134 3,p31=-0.001 389,p22=-0.001 739,p13=-0.000 510 8,p50=-2.799×10-6,p41=-6.955×10-6,p32=1.17×10-6,p23=1.335×10-5。
上述拟合的置信度为95%,方差为4.085。
3 结 论
1)热源移动速度较低时,加热功率对弯曲角度影响较小。随着热源移动速度的增加,功率越大,成形角度越大。加热功率较大时,钢板弯曲角度随着热源移动速度增加先增大再减小,而加热功率较小时钢板弯曲角度随着热源移动速度增加直线下降,没有出现峰值。
2)热源移动速度较低时,加热功率对弯曲曲率半径影响不大;随着热源移动速度的增加,钢板弯曲曲率半径增大;加热功率越小,曲率半径越大。
[1] 周宏,罗宇,蒋志勇.船舶板材边界条件对高频感应弯板成形的影响[J].船海工程,2009,38(5):19-23.
ZHOU Hong, LUO Yu, JIANG Zhiyong. Influence of boundary condition on high frequency inducting plate bending [J].Ship&OceanEngineering, 2009, 38(5): 19-23.
[2] 纪卓尚,刘玉君,孙振烈,等.船体曲面钢板水火加工成型工艺的理论与应用研究[J].中国造船,1998(增刊):118-124.
JI Zhuoshang, LIU Yujun, SUN Zhenlie, et al. Study on theory and application for hull steel plate bending by line heating[J].ShipbuildingofChina, 1998(Sup): 118-124.
[3] 张雪彪.船体曲面钢板完全线加热成形研究[D].大连:大连理工大学,2006.
ZHANG Xuebiao.ResearchonShip-hullCurvedPlateFormingbyPureLineHeating[D].Dalian:Dalian University of Technology,2006.
[4] BAE K Y, YANG Y S, HYUN C M, et al. Derivation of simplified formulas to predict deformations of plate in steel forming process with induction heating [J].InternationalJournalofMachineToolsandManufacture, 2008, 48(15): 1646-1652.
[5] LEE J H, LEE K H, YUN J S. An electromagnetic and thermo-mechanical analysis of high frequency induction heating for steel plate bending[J].KeyEngineeringMaterials,2006,326/328:1283-1286.
[6] JANG C D, KIM H K, HA Y S. Prediction of plate bending by high-frequency induction heating [J].JournalofShipProduction, 2002, 18(4): 226-236.
[7] 张继祥,殷筱依,刘凤芝,等.纤维增强薄壁塑件翘曲变形分析[J].重庆交通大学学报(自然科学版),2016,35(4):173-178.
ZHANG Jixiang, YIN Xiaoyi, LIU Fengzhi et al. The analysis of the warpage of thin-wall plastic part for fiber reinforced plastic [J].JournalofChongqingJiaotongUniversity(NaturalScience), 2016, 35(4): 173- 178.
[8] 刘芳平,周建庭.变截面开口薄壁钢箱稳定性分析[J].重庆交通大学学报(自然科学版),2012,31(6):1105-1108.
LIU Fangping, ZHOU Jianting. Stability analysis of open thin-walled steel box with variable cross-section[J].JournalofChongqingJiaotongUniversity(NaturalScience), 2012, 31(6): 1105-1108.
[9] 范平,陈明和,周兆峰,等.板料无模成形技术—热应力成形[J].新技术新工艺,2007(11):62-64.
FAN Ping, CHEN Minghe, ZHOU Zhaofeng, et al. Dieless thermal stress forming of plate [J].NewTechnology&NewProcess, 2007(11): 62-64.
[10] 张继祥,安国银,李政君,等.不同厚度下船舶板材高频感应自由弯曲成形[J].重庆交通大学学报(自然科学版),2012,31(4):900-904.
ZHANG Jixiang, AN Guoyin, LI Zhengjun et al. Free bending of ship plate of different thickness on high-frequency induction[J].JournalofChongqingJiaotongUniversity(NaturalScience),2012,31(4): 900- 904.
[11] 安国银,张继祥,李政君,等.船板高频感应加热关键点变形规律研究[J].船舶工程,2013,35(5):87-89.
AN Guoyin, ZHANG Jixiang, LI Zhengjun, et al. Study of deformation law of key points on high-frequency induction heating for ship plate [J].ShipEngineering, 2013, 35(5): 87-89.
[12] 张雪彪,杨玉龙,刘玉君,等.钢板弯曲工艺中的高频感应加热过程数值分析[J].中国造船,2011,52(2):108-116.
ZHANG Xuebiao, YANG Yulong, LIU Yujun, et al. Process applied to steel plate bending technology[J].ShipbuildingofChina,2011, 52(2): 108-116.
[13] 张雪彪,杨玉龙,刘玉君.钢板高频感应加热过程电磁-热耦合场分析[J].大连理工大学学报,2012,52(5):676-682.
ZHANG Xuebiao, YANG Yulong, LIU Yujun. Analysis of electromagnetic - thermal coupling field for high frequency induction heating process of steel plate [J].JournalofDalianUniversityofTechnology, 2012, 52(5): 676-682.
[14] 周宏,蒋志勇.表面换热系数对高频感应弯板成型的影响[J].材料热处理学报,2013,34(增刊Ⅱ):262-266.
ZHOU Hong, JIANG Zhiyong. Effect of high frequency induction technology-based model surface heat exchange coefficient on bending plate forming of ship hull [J].TransactionsofMaterialsandHeatTreatment, 2013, 34(SupⅡ): 262-266.
[15] 张继祥,徐昱,王智祥,等.钢板高频感应移动加热成形有限元建模及模拟研究[J].锻压技术,2014,39(7):40-46.
ZHANG Jixiang, XU Yu, WANG Zhixiang, et al. Finite element modeling and simulation research of high frequency induction heating forming of steel plate based on moving heat source [J].Forging&StampingTechnology, 2014, 39(7): 40-46.
[16] 张继祥,杨泮,刘凤芝,等.跟踪水冷下钢板高频感应三维移动加热成形有限元模型研究[J].锻压技术,2015,40(7):113-119.
ZHANG Jixiang, YANG Pan, LIU Fengzhi, et al. Research on finite element model of 3D mobile tracking water-cooling steel plate with high frequency induction in the heating forming process with high frequency induction [J].Forging&StampingTechnology, 2015, 40(7): 113-119.
[17] 徐昱.三维移动式感应加热弯板成形有限元模拟研究[D].重庆:重庆交通大学,2015.
XU Yu.StudyonFiniteElementSimulationofThree-DimensionMovingInductiveHeatingPlateBendingForming[D].Chongqing:Chongqing Jiaotong University, 2015.
EffectsofParametersofInductionHeatingProcessonBendingAngleandRadiusofCurvatureofQ345Steel
ZHANG Jixiang1, 2, ZHOU Wei1, XU Yu1, ZHONG Li1, 2
(1.School of Mechatronics & Vehicle Engineering, Chongqing Jiaotong University, Chongqing 400074, P. R. China; 2.Chongqing Engineering Research Center for Special Ship Digital Design and Manufacturing, Chongqing Jiaotong University, Chongqing 400074, P. R. China)
Based on the finite element analysis software ANSYS and its APDL language, an electric-magnetic-heat-stress physic field coupling in the HFV (high frequency induction) heating formation was realized and a finite element model of three-dimensional mobile high frequency induction heating bending plate was established. The relationship between HFV bending plate forming targets and their process parameters was systematically studied. The results show that the steel plate bending angle increases first and then decreases with the increase of the heat source moving speed when the heating power is large; while, the bending angle decreases sharply with the increase of heat source moving speed when the heating power is relatively small. The radius of curvature of steel plate increases with the increase of heat source moving speed, and decreases with the increase of heating power. Finally, the function formula of the bending angle with the heating power and the heat source moving speed, and that of the curvature radius with the heating power and the heat source moving speed were established respectively.
ship engineering; FEM simulation; high frequency induction; bending plate formation; function formula
10.3969/j.issn.1674-0696.2017.11.20
2016-04-13;
2016-06-29
重庆市基础前沿研究计划项目(cstc2013jcyjA70015);重庆市教育委员会科学技术研究项目(KJ080407)
张继祥(1971—),男,山东单县人,教授,博士,主要从事材料加工和机械工程方面的研究。E-mail: jixiangzhang@163.com。
周 伟(1990—),男,安徽砀山人,硕士研究生,主要从事机械工程方面的研究。E-mail: 42528256@qq.com。
U671.6;TG 161
A
1674-0696(2017)11-106-05
(责任编辑:刘韬)

