车辆吊耳支架结构优化分析研究

刘勺华，邵亭亭，路纪雷

(1.常州机电职业技术学院 车辆工程学院，江苏 常州, 213164；2.南京徐工汽车技术中心，江苏 南京 210012)

车辆吊耳支架结构优化分析研究

刘勺华1，邵亭亭1，路纪雷2

(1.常州机电职业技术学院 车辆工程学院，江苏 常州, 213164；2.南京徐工汽车技术中心，江苏 南京 210012)

大多数重型车辆均采用吊耳支架将悬挂系统与车架连接，为车架与悬挂系统的关键承载零件之一。基于拓扑优化理论及有限元方法，使用Hyperworks中OptiStruct优化设计模块，对吊耳支架进行了拓扑优化，以在强度允许的前提下取得最佳的材料分布，使得质量最小。优化后进行了CAD模型重构，经与原件的静强度和模态比较结果表明：新设计的零件较原零件质量降低34.07%，一阶模态提高6.81%，最大应力降低5.38%。此优化方法对车辆结构设计改进具有实际工程指导意义。

车辆工程；吊耳支架；拓扑优化；Hyperworks；模型重构

0 引 言

随着消费者对汽车车速和油耗的日渐关注，汽车轻量化已经越来越被各汽车厂家所重视。笔者借助Altair公司旗下的Hyperworks软件，对重卡汽车普遍采用的吊耳支架进行应力约束下的拓扑优化设计，以在强度允许的前提下取得最佳的材料分布，使得质量最小。通过整个设计分析流程证明，任何汽车零件都有优化设计的空间，新车设计时应当充分考虑汽车的轻量化问题。

笔者以国内重型车辆吊耳支架为研究对象，借助CAE分析手段对该装置进行建模、优化、分析、重构，使其强度符合要求，重量降低。强度分析结果表明，利用CAE软件进行吊耳支架优化研究可以改善结构设计，提高汽车的自身重量，从而缩短开发周期，降低开发费用，提高市场竞争力[1-3]。

1 有限元模型的建立

1.1 优化前吊耳支架建模

吊耳支架是重型车上连接悬挂系统与车架的，起着传递纵向力，承载垂向力的作用。目前大多重型车上的吊耳支架均为铸造件。将CATIA中某现有的吊耳支架三维实体模型转换成iges格式后导入Hypermesh中进行有限元的前处理—网格划分[4-5]。为了得到高质量的网格，在划分之前将实体模型拆分成易于划分六面体的单个实体的组合。最后得到图1的吊耳支架模型，模型包含77 135个实体单元，35 431个节点。

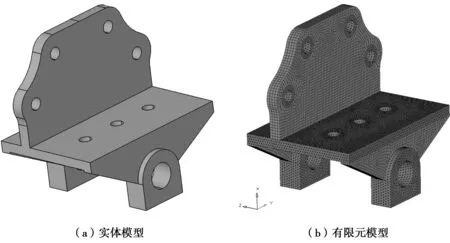
图1 优化前吊耳支架模型Fig.1 Lug bracket model before optimization

1.2 边界条件

吊耳支架在实际使用时，是将Z方向的4个孔与纵梁侧面连接，X方向的3个孔与纵梁下翼面连接，下方2个3角形支撑板上的孔连接板簧，如图2。在汽车的实际运行过程中，吊耳支架的受力情况比较复杂。按照不同工况分类，吊耳支架大致可分为垂直上跳、垂直下跳、制动和侧向力4种工况。因此，在分析时，约束情况是将吊耳支架端面3个螺栓孔及侧面4个螺栓孔自由度全部设为0，至于载荷的加载则根据不同的工况在安装板簧的销孔处施加不同方向的力。

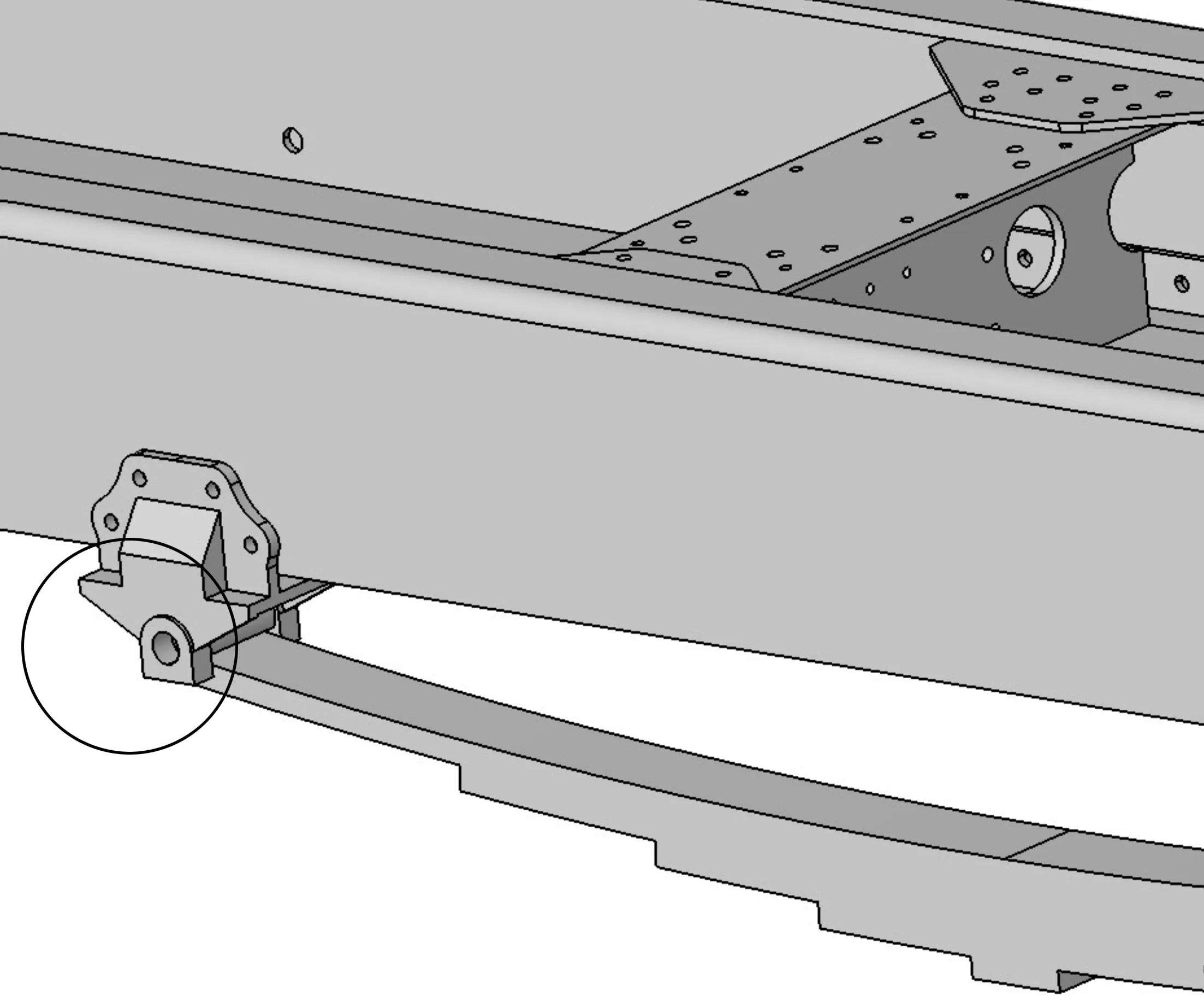
图2 吊耳支架安装位置示意Fig.2 Mounting position of lug bracket

1.3 计算结果

划分完网格，施加约束及载荷条件后将有限元模型导入到Hyperworks的optistruct模块进行求解，得到已有吊耳支架的应力云图，如图3。

图3 吊耳支架强度校核Fig.3 Strength check of lug bracket

2 吊耳支架拓扑优化

2.1 分设计与非设计区域

由图3可以看出，现有的吊耳支架最大应力为167.34 MPa，远远低于材料的许用应力355 MPa。因此，该构件有较大的优化空间。但是考虑到构件与其他零件之间的连接，需要设定设计区域和非设计区域，其中非设计区域不在优化范围。图4为划分区域之后，待优化的吊耳支架有限元模型。

图4 划分设计区域和非设计区域Fig.4 Division of design and non-design region

图4中7个圆柱形区域为螺栓安装部位，是非设计区，其他区域为设计区。分别为设计区域和非设计区域划分网格之后还要将2个区域的网格节点耦合，通过这种方法将设计区域和非设计区域合成一体。

2.2 优化的数学模型

优化设计有3要素，即设计变量、目标函数和约束条件。优化设计的数学模型可表述为

f(X) =f(x1,x2，…，xn)

(1)

约束条件：

L≤xi≤Ui= 1,…,n

(2)

g(X)<0

(3)

式中：X=x1,x2，…，xn为设计变量；f(X)是目标函数；L为变量下限；U为变量上限；g(X)为不等式约束函数。

在优化中，目标函数f(X)，约束函数g(X)是从有限元分析中获得的结构响应。设计变量X是一个矢量，它的选择依赖于优化类型。在拓扑优化中，设计变量为单元的密度[6-8]。Optistruct结构优化设计的具体流程如图5。

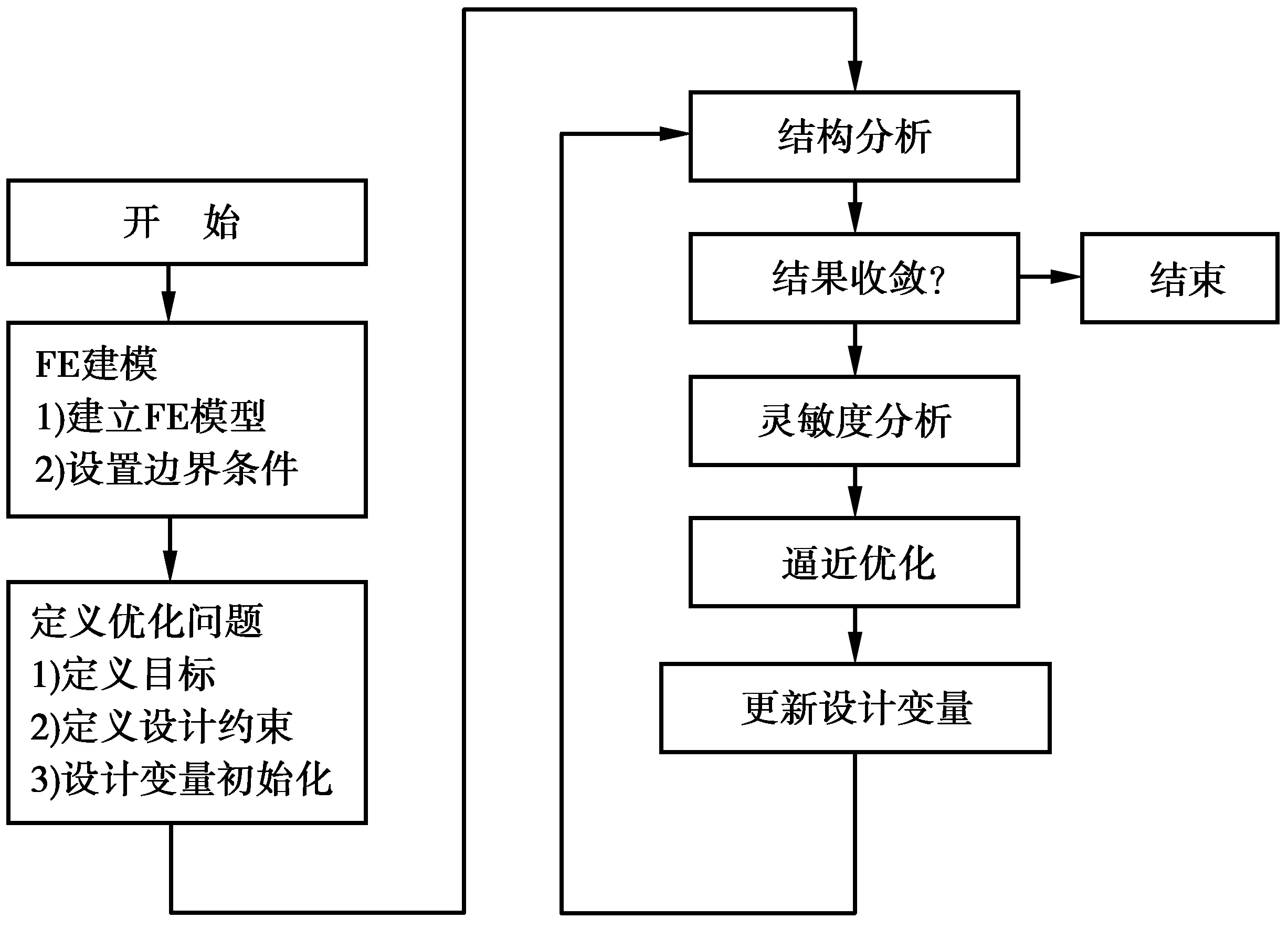
图5 结构优化设计流程Fig.5 Design flow of structure optimization

3 拓扑计算及零件重构

3.1 优化结果

前处理完成后调用Optistruct模块进行分析。体积分数沿迭代次数的变化在第17次迭代之后，结果收敛，优化过程结束。打开Hyperview，查看第17步的优化结果(单元密度阈值取0.1)，如图6[9-11]。

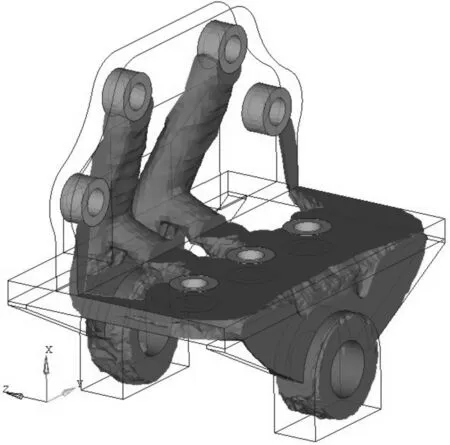
图6 优化结果Fig.6 Optimization result

3.2 零件重构

返回HyperMesh窗口，在后处理Post 面板将第17步结果读入，并使用OSSmooth 命令将优化后的单元格光顺成ISO 曲面，ISO 曲面阀值同样取0.1，

光顺结果如图7(a)。参考输出的曲面，在CATIA中对零件进行重构，得到新设计的零件，如图7(b)。

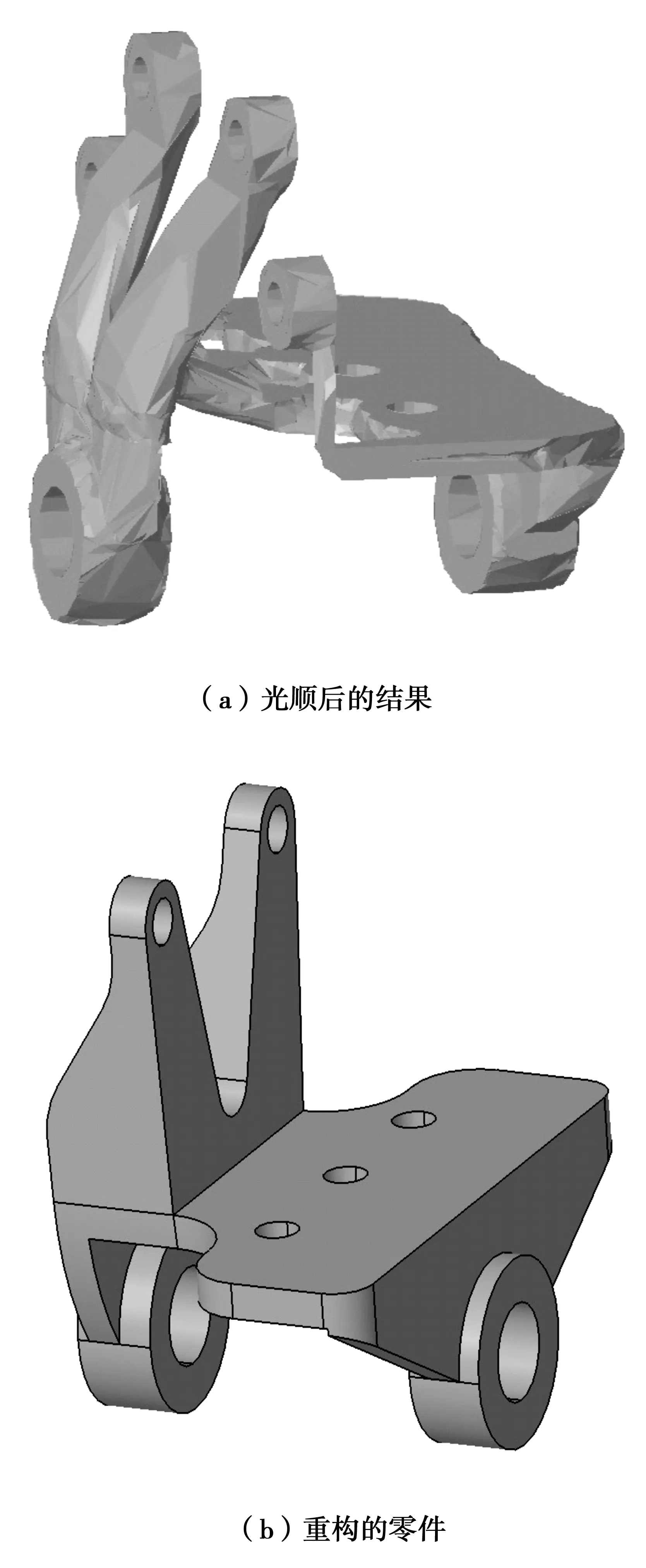
图7 零件重构Fig.7 Parts reconstruction

4 重构模型验证

重新构造的模型还需要CAE分析验证，与原零件对比。如果经对比分析，新设计零件比原零件具有优势，设计方案才算完结。新设计零件4种工况下的的应力分布云图，如图8。

图8 新零件吊耳支架强度校核Fig.8 Strength check of new part lug bracket

将原零件与新零件分析结果进行3方面对比得表1。

表1原零件与新设计零件对比

Table1Comparisonoforiginalpartandnewdesignpart

零件质量/kg最大应力/MPa最大应力工况原支架新支架6．814．49169163侧向力工况

笔者是借助 CAE 分析手段对该构件进行分析、重构，使其构件轻量化，为设计改进提供了重要参考依据。这种方法对于整车企业缩短开发周期，降低开发费用，提高市场竞争力很有帮助。在实践应用过程中，模拟计算结果也基本上与实际受力过程相一致,仿真所用的外力是汽车实际使用过程中的极限工况下的最大载荷。当极限工况下部件受力情况满足使用要求时，普通工况也能满足。

影响材料疲劳性能的因素除最大应力外，还有构件尺寸、表面光洁度、表面处理、使用温度及环境等其他因素。根据名义应力应变法及材料S-N曲线，当影响因素一致时，最大应力降低，疲劳寿命肯定会有所提高。

5 结 语

笔者在CATIA中建立了重型车辆吊耳支架三维模型，并利用Hyperwoks软件建立有限元模型，对吊耳支架4种常见工况进行强度校核分析，并进行了吊耳支架拓扑优化，拓扑计算及零件重构。经过对比，新设计的零件较之原零件质量降低34%、最大应力降低3.5%。新设计的零件不仅能满足强度要求，而且其质量比原件有所降低。笔者通过完整的流程证明了只要是零部件就可能存在优化的空间，为车辆轻量化研究提供一定的理论依据，本优化方法对车辆结构设计改进具有实践工程指导意义。

[1] 刘勺华,房亚，路纪雷，等. 汽车后防护装置有限元强度分析研究[J].重庆交通大学学报(自然科学版),2015,34(2): 137-140.

LIU Shaohua, FANG Ya, LU Jilei, et al. Finite element strength analysis of automotive rear defend device[J].JournalofChongqingJiaotongUniversity(NaturalScience), 2015, 34(2): 137-140.

[2] 上官文斌,黄志,贺良勇，等.汽车排气系统吊耳动刚度优化方法的研究[J].振动与冲击,2010,29(1): 100-102,152.

SHANGGUAN Wenbin, HUANG Zhi, HE Liangyong, et al. Modeling and optimization method of dynamic stiffness for automotive exhaust system hangers[J].JournalofVibrationandShock, 2010, 29(1): 100-102,152.

[3] 李卓，周劲松，张学铭，等. 地铁车辆轴箱吊耳动态分析和优化[J].计算机辅助工程，2012,21(1): 27-31.

LI Zhuo, ZHOU Jinsong, ZHANG Xueming, et al. Dynamic analysis and optimization of lifting lug fixed to axle box of metro vehicle[J].Computer Aided Engineering, 2012, 21(1): 27-31.

[4] BELYTSCHKO T , LIU W K,MORAN B. 连续体和结构的非线性有限元[M].庄茁，译.北京:清华大学出版社, 2002.

BELYTSCHKO T, LIU W K, MORAN B.NonlinearFiniteElementsforContinuaandStructures[M].ZHUANG Zhuo, translation. Beijing: Tsinghua University Press, 2002.

[5] 王勖成,邵敏.有限单元法基本原理和数值方法[M].北京:清华大学出版社, 2003.

WANG Xucheng, SHAO Min.TheBasicPrinciplesoftheFiniteElementMethodandNumericalMethods[M].Beijing: Tsinghua University Press, 2003.

[6] 柴山，郭明，徐上海，等. 车辆钢板弹簧悬架的有限元模型[J].江苏大学学报(自然科学版),2015,36(1): 16-22.

CHAI Shan, GUO Ming, XU Shanghai, et al. Finite element models for vehicle leaf spring suspensions[J].JournalofJiangsuUniversity(NaturalScienceEdition), 2015, 36(1): 16-22.

[7] 尚志诚，胡 葳，刘一鸣. 重型牵引车空气悬架钢板弹簧支架强度分析与优化[J].客车技术与研究,2015(3): 4-7.

SHANG Zhicheng, HU Wei, LIU Yiming. Strength analysis and optimization on leaf spring holder in air suspension of heavy traction vehicle[J].Bus&CoachTechnologyandResearch, 2015(3):4-7.

[8] 肖乾，方骏，谭祖宾，等. 铁路轨检车轴箱振动特性分析[J].铁道机车车辆，2015,35(2): 10-13.

XIAO Qian, FANG Jun, TAN Zubin, et al. Axle-box vibration characteristic analysis for a railway track inspection vehicle[J].RailwayLocomotive&Car, 2015, 35(2): 10-13.

[9] 赵婷婷，李长波，王军杰，等. 基于有限元法的某微型货车车身疲劳寿命分析[J].汽车工程，2011,33(5): 428-432.

ZHAO Tingting, LI Changbo, WANG Junjie, et al. Fatigue life analysis of a mini truck body based on FEM[J].AutomotiveEngineering, 2011, 33(5): 428-432.

[10] 张仁斌, 黄义勇, 成全胜. 基于 ABAQUS 的某微型车辆转向支架优化分析[J].机械设计与制造，2012(7): 191-193.

ZHANG Renbin, HUANG Yiyong, CHENG Quansheng. Optimization analysis of micro-car steering bracket based on ABAQUS[J].MachineryDesign&Manufacture, 2012(7): 191-193.

[11] 李乐新，沈智达，雷济平. 安全气囊ECU支架的频响分析及模态优化[J]. 机械设计与制造，2012(4): 273-275.

LI Lexin, SHEN Zhida, LEI Jiping. Frequency response analysis and modal optimization of airbag CEU bracket[J].MachineryDesign&Manufacture, 2012 (4): 273-275.

OptimizationAnalysisonVehicleLugBracketStructure

LIU Shaohua1, SHAO Tingting1, LU Jilei2

(1.School of Automobile Engineering, Changzhou Institute of Mechatronic Technology, Changzhou 213164, Jiangsu, P.R.China; 2.Nanjing Xugong Automobile Manufacturing Co. Ltd., Nanjing 210012, Jiangsu, P.R.China)

As one of key bearing parts of the suspension system and the frame, lug bracket was used by most heavy vehicles to connect the suspension system and the frame. Based on topology optimization theory and finite element method, Optistruct in Hyperworks was used to carry out the module design optimization, and the topology optimization of lug bracket was carried out, which was expected to obtain the optimal material distribution and a minimum mass in the premise of strength permit. After optimization, CAD model reconstruction was carried out. Compared with the static strength and modal of original, the results show that compared with the original parts, the quality of the new designed parts is reduced by 34.07%, the first order mode is improved by 6.81%, and the maximum stress is decreased by 5.38%. The proposed optimization method has practical engineering guidance for the improvement of vehicle structure design.

vehicle engineering; lug bracket; topology optimization; Hyperworks; model reconstruction

10.3969/j.issn.1674-0696.2017.11.19

2016-05-18；

2016-11-21

国家自然科学基金项目(51375212) ; 江苏省高校自然科学基金项目(16KJB580012);2016年江苏省高校优秀中青年教师境外研修项目

刘勺华(1982—)，男，山东临沂人，讲师，博士研究生，主要从事车辆动态性能模拟与控制方面的研究。E-mail:99954886@qq.com。

TP391.9；U464.134+.4

A

1674-0696(2017)11-100-06

(责任编辑：谭绪凯)