微观量子器件中分子马达单向转动的条件机理研究
宋亚峰,朱勤生,焦壮壮,孔雄雄,李辉杰
(1. 商洛学院 电子信息与电气工程学院物理系,陕西 商州 726000; 2. 中国科学院半导体研究所材料重点实验室,北京 100083)
微观量子器件中分子马达单向转动的条件机理研究
宋亚峰1,朱勤生2,焦壮壮1,孔雄雄1,李辉杰2
(1. 商洛学院 电子信息与电气工程学院物理系,陕西 商州 726000; 2. 中国科学院半导体研究所材料重点实验室,北京 100083)
微观量子器件中的分子马达是微观机械系统与纳米器件领域的重要器件,深入系统地研究了其单向转动的条件及机理。先从几何的角度分析了宏观棘轮工作的物理本质,得出了3个必要条件。之后开始讨论微观棘轮,将热涨落对其的影响归在第3个条件。接着具体分析了温度T较低、T较高无外界作用、T较高有较大外界作用3种情形下的不同机理。着重分析了第3种情形下斜面特性是如何实现对原本无极性的外界作用进行了“整流”。最后得出微观棘轮单向转动的两个必要条件为:体系的非平衡性(内因)和存在适当的极性结构(外因)。这些结论可以为相关的微观量子器件中的纳米器件的设计及应用提供有益的参考。
分子马达;棘轮;热涨落;热力学第二定律
近年来,随着半导体微电子领域对微米向纳米尺度的深入发展,一系列微观尺度的量子器件应运而生。在各种微观量子器件中,量子尺度的分子马达越来越成为近年来一个持续的研究热点[1-13]。微观量子器件中的分子马达是微观机械系统与纳米器件领域的重要器件,在微纳机械电子器件系统中及量子生物物理领域有重要的应用前景。这其中,分子马达在微观领域转动的单向“整流”特性尤其一直是影响其应用前景的一个非常重要的基本问题,因此引起了很多这方面的研究[3-8,12]。分子马达的典型模型可以用微观尺度的棘轮来描述,即所谓的费曼棘轮(Feynman’s 棘轮)[1]。对此我们进行了系统深入的分析和研究。
1 建模过程及结果分析
1.1宏观棘轮的物理本质
我们对比图1 a和b得棘轮单向转动的必要条件1:棘轮齿形状的不对称性。由图1c、图2a得必要条件2:棘爪端部轨迹最低点A应低于棘轮内包络圆最高点C。对比图1 a、c和图2b得必要条件3:弹簧原长时棘爪顶部P0点应位于棘轮的外包络圆内,即棘轮和棘爪要具有直接接触的机会。分析可知,条件2才是产生单向转动的最本质的条件,可以认为,凡满足条件2的机构都是广义棘轮。但本文只讨论图1a所示的最一般意义上的棘轮,即狭义棘轮。对于宏观棘轮来说,其发生单向转动的必要条件一可以描述为环境的各向异性或轨道要提供稳定的极性。必要条件2、3可以归纳为发生了不可逆过程。

a本文所讨论的棘轮;b“向日葵轮”;c一种可双向转动的棘轮结构

a另一种可双向转动的棘轮结构;b可以单向转动的棘轮
1.2微观量子尺度分子马达基本情况分析
鉴于本文所要讨论的分子马达为图1a所示的狭义棘轮,所以他应满足必要条件1、2。我们知道,热涨落对于分子马达是不可避免的,这是与宏观机器最大的不同之处。显然热涨落直接影响到棘爪顶端与棘轮齿之间的相对位置,即影响必要条件3是否满足。因此,我们认为,热涨落主要通过必要条件3来影响棘轮最终是否可以单向转动。
具体来说,热涨落主要影响两点:提供让棘轮正转和反转的原动力,并且正转和反转的几率相等;使棘爪尖端P点上下跳跃。此处我们考虑的是理想情况:棘爪和棘轮的转轴的相对距离是不变的,即图1 a中的圆心距O1O2始终不变。
1.3分子马达的3种情形
如图3所示,我们把问题分为以下3种情形。

a 情形i,T较高; b 情形ii,T较低,无外界作用; c 情形iii,T较低,有较大外界作用
图33种不同情形下的棘轮单向转动分析
情形i(图3a)温度T较高时,热涨落足以使P点在弹起足够高,以致于P点到了棘轮的外包络圆之外,并维持较长时间,相当于不满足条件3(如图3a)。显然,棘轮可以自由正转或反转,净效果是不会单向转动(这一点可以通过T→∞来设想)。
情形ii(图3b)T很低,且没有外界作用时,热涨落并不能使P点弹起足够高,P点始终在棘轮的外包络圆内,虽然满足条件3,但条件1、2、3只是必要条件。由于此时T很低,系统能量很有限,既然不能使棘爪弹得足够高,也就没有理由是棘轮克服棘爪弹簧的“势垒”而转过一个齿。因为棘轮的涨落和棘爪的涨落在统计意义上是相对独立的,二者并不没有谁比谁更占优。而且二者本来就不可区分,因为热平衡系统中只区分状态不区分过程。因此此时实际上是棘轮棘爪被冻结了,系统的能量不足,棘轮连一个齿都转不了,净效果也是不会单向转动(这一点可以通过T→0来设想)。
对比情形i和ii,我们知道,只要没有外界作用(即体系处于平衡状态),无论T较高还是较低,棘轮都不会单向转动。但其实二者的机理并不相同,前者是由于热涨落使必要条件3不满足,后者虽然3个条件都满足,但能量不足,系统处于被冻结状态。可以看到只要是热平衡系统,光凭系统本身不会实现将热不断转化成功而不引起其他变化的,这正是热力学第二定律所描述的。
情形iii(图3c)当T较低但有某种较大的外界作用中的外界作用时,外界可以提供棘轮转动的额外动力,他使棘轮正、反转的几率是一样的。但下面“四”中的分析将会看到,由于“单侧斜面的几何特性”对这个动力进行了“整流”,使棘轮想要反转时出现自锁,能量就耗散掉了;而当它想正转时正好借助于斜面的作用实现正转。净效果就是棘轮实现了单向转动。
对比情形ii和iii,可以看到正是由于iii中系统处于非平衡状态,才使它现了单向转动。
2 逻辑分析及举例
为方便起见,我们将较高的温度全记为T,较低的温度记为t,例如出现T1,t2(则有T1>t2)。将图4a和图4b中的1、2点用理想杆(刚性绝热)连接,即得费曼棘轮[1](图4c)我们知道,后者能单向正转。此时对比各图,可知图4c中的棘爪与图3a中的温度相同,图4c中的叶轮与图3c中的温度相同;

a棘轮不单向转;b叶轮不单向转;c棘轮正转
而另一方面,可以近似地认为,由于理想杆的作用,图4c中的棘轮和图3c中的叶轮温度相同,这样,我们就得到实际上图4c中的棘轮温度为T2,棘爪温度为t1,二者温度并不相同,系统为非平衡状态。相比之下,图4a、b各自都是平衡系统。这一点是只有图4c产生单向转动的原因。因此可得微观棘轮单向转动的必要条件I(内因):系统的非平衡性。
但是,是否系统具备非平衡性就一定会产生单向转动呢?显然不是。我们来看图5和图6。图5的叶轮显然不会单向转动。由于图中的叶轮及轴只起着机械连接的作用,并不传导热。所以当考虑系统变化非常缓慢的准静态过程时很容易让人误以为系统可以看成是可逆过程。

图5 叶轮不单向转动
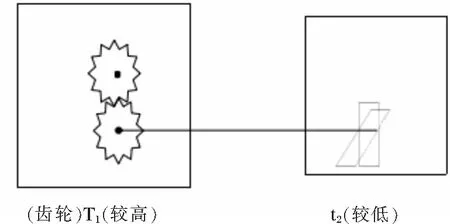
图6 齿轮不单向转动
我们知道卡诺循环是可逆过程,所以得到费曼棘轮也是可逆的。如文献[2]所言,不应该混淆准静态和可逆这两个概念。事实上非平衡条件下的准静态过程不可逆。这一点可以从下面的角度来分析:
图5中,尽管叶轮和轴不直接传热,但两箱中的气体分子都在不停地和叶轮相互碰撞。由于T1较高,左箱中气体分子振动得更剧烈,故它撞击叶轮a更剧烈,对于理想叶轮,则在叶轮a的带动下,叶轮b也振动得同样剧烈,它就会主动撞击比它温度更低的右箱气体分子,将能量传给b箱。所以可以说叶轮a占主动,通过理想杆向叶轮b周围的气体分子输出功,后者吸收功后热运动更加剧烈,温度升高,同时a箱中的气体温度在降低。显然,只要时间足够长,两箱气体的温度将趋于一致。整个过程实际上正是一个由非平衡态自发回到平衡态的过程。与a、b中的气体通过热传递达到同一温度并没有本质的区别。由此可见,热传递的微观本质就是微观运动,也是一种广义的做功,只不过所做的功可以称为“无序功”,直接由系统自身耗散掉了,不能被直接有效利用为人类服务。
同样,图6中齿轮也不会单向转动。对比图5、6与图4c、图7c,可得微观棘轮单向转动的另一个必要条件(外因):存在适当的极性结构(如单侧斜面)对非平衡作用进行“整流”。这是一种狭义的做功,所做的功为有序功,可以对外输出,被直接有效利用为人类服务。同理,若我们将图7a和b中的3、4点用理想杆连接,就成了图7c。显然,与图4c一样,图7c中也是棘轮温度T1,棘爪温度t2,故棘轮也是正转。
同样,若将图7a、c中的棘轮、棘爪互换,会怎样?得到图8。对比图7c棘轮和图8b棘轮会发现,图8b中的棘轮应为反转,因为棘爪温度比棘轮高,能量是从棘爪传到棘轮的,棘爪为主动,导致棘轮反转。
3 深入分析及总结
换句话说,棘轮转动和棘爪跳动在统计意义上是独立无关的两个事件,但在平衡态,二者无论温度谁高谁低,高的一方将对低的一方做功(广义的做功)。这种做功通常有两种表现。直接表现:一方比另一方振动得更剧烈,没有净单向转动(所做的是“无序功”),棘轮不单向转动。附加表现:在存在合适的极性结构(棘轮那样的单侧斜面),后者对非平衡作用进行了 “整流”(所做的是“有序功”)棘轮单向转动。表现结果是热棘轮使自己正转,热棘爪使冷棘轮反转。

a 棘轮不单向转; b 叶轮不单向转; c 棘轮正转

图8 叶轮与棘轮连接、棘轮温度高于叶轮温度的费曼棘轮分析:棘轮正转
4 结 论
微观量子器件中的分子马达是微观机械系统与纳米器件领域的重要器件,在微纳机械电子器件系统中及量子生物物理领域有重要的应用前景。本文从宏观棘轮的几何特性出发分析了微观棘轮在热涨落下单向转动的条件及其机理。结果得出了微观棘轮单向转动的两大必要条件为:体系的非平衡性,即发生了不可逆过程(内因);和存在适当的极性结构(如单侧斜面)对非平衡作用进行“整流”,即环境的各向异性或轨道要提供稳定的极性(外因)。这些结论可以为相关的微观量子器件中的纳米器件的设计及应用提供有益的参考。
[1] Rechard F. 费曼物理学讲义第一卷[M]. 上海:上海科学技术出版社,2013.
[2] Parrondo, Juan M R, Espaol Pep. Criticism of Feynman‘s analysis of the ratchet as an engine[J]. American Journal of Physics, 1996, 64(9): 1125-1130.
[3] 田茎.分子马达定向运动机制的研究[D]. 郑州:郑州大学,2007.
[4] 施夏清,马余强.活力物质的非平衡结构和动力学[J]. 物理,2012,41(1):31-38.
[5] 文书堂.分子马达定向运动物理机制研究[D]. 郑州:郑州大学,2004.
[6] 葛荣春.少体系统的量子关联和量子棘轮[D]. 合肥:中国科学技术大学,2012.
[7] 冯玉宇.耦合布朗马达的定向运输研究[D]. 西安:西北农林科技大学,2015.
[8] 白文斯密,彭皓,屠浙.分数阶Brown马达及其定向输运现象[J]. Acta. Phys. Sin.,2012,61(21): 64-69.
[9] 程海涛.热驱动布朗马达的热力学性能研究[D]. 南昌:南昌大学,2012.
[10] 陈磊.多光子干涉与量子棘轮效应[D]. 合肥:中国科学技术大学,2010.
[11] 陈良林.对称周期势场中粒子输运的数值模拟研究[D]. 昆明:云南大学,2013.
[12] 王莉芳,高天附,黄仁忠. 外力作用下反馈耦合布朗棘轮的定向输运[J]. Acta. Phys. Sin.,2013, 62(7): 63-68.
[13] 程海涛,何济洲,肖宇玲. 周期性双势垒锯齿势中温差驱动的布朗热机[J]. Acta. Phys. Sin., 2012, 61(1): 53-58.
StudyontheConditionMechanismofOne-wayRotationofMolecularMotorinMicroscopicQuantumDevices
SONG Yafeng1, ZHU Qinsheng2, JIAO Zhuangzhuang1, KONG Xiongxiong1, LI Huijie2
(1.DepartmentofPhysics,CollegeofElectronicInformationandElectricalEngineering,ShangluoUniversity,Shangzhou,Shanxi726000,China;2.KeyLaboratoryofSemiconductorMaterialsScience,InstituteofSemiconductors,ChineseAcademyofSciences,Beijing100083,China)
The molecular motor in microscopic quantum device is an important device in the field of micro-mechanical system and nanometer device. In this paper, the conditions and mechanism of one-way rotation are studied systematically. This paper analyzes the physical essence of macro ratchet work from the perspective of geometry. It obtains three necessary conditions. Two necessary conditions for one-way rotation of the microscopic ratchet read as follows: the non-equilibrium (internal) of the system and the proper polarity structure (external factor). These conclusions can provide a useful reference for the design and application of nanometer devices in related micro quantum devices.
Molecular motor; Ratcheting wheel; Heat fluctuation; Second law of thermodynamics
2017-07-13
国家自然科学基金项目(Nos.61504128,61504129,61274041,11275228);陕西省自然科学基础研究计划资助项目(2017JQ6011);商洛市科技局科研计划资助项目(SK2015-35);商洛学院科学与技术研究基金项目(15SKY025)。
宋亚峰(1984-),男,山西介休人,博士,讲师,研究方向:半导体低维结构与器件研究,电话:0914-2986020,E-mail:cumtsyf03@163.com.
TN389;TH136
A
10.14101/j.cnki.issn.1002-4336.2017.05.032

