恐怖袭击事件中悲观/乐观情绪如何影响博弈均衡结果

刘德海，鲍雪言，王谢宁

(1．东北财经大学管理科学与工程学院，辽宁 大连 116025；2. 东北财经大学经济计量分析与预测研究中心，辽宁 大连 116025)

恐怖袭击事件中悲观/乐观情绪如何影响博弈均衡结果

刘德海1,2，鲍雪言2，王谢宁1

(1．东北财经大学管理科学与工程学院，辽宁 大连 116025；2. 东北财经大学经济计量分析与预测研究中心，辽宁 大连 116025)

恐怖袭击事件对人类社会的文明底线构成了严峻挑战。无论恐怖分子还是政府反恐力量，双方均具有非常明显的情境决策、甚至非理性决策的特征。本文基于等级依赖期望效用理论，分析了恐怖分子和政府反恐力量对于事态发生的主观概率具有乐观或者悲观预期时，情绪因素对于传统博弈均衡结果的影响，以及该理论结果对于完善反恐措施的管理含义。研究结果表明，当仅有某一方存在着乐观或者悲观情绪时，能够准确地研判事态发生概率的对手将调整选择策略的均衡概率，即任何一方的情绪因素都将影响到对手的策略选择。当双方都存在着情绪因素时，存在乐观情绪的恐怖分子更加倾向于采取非理性的冒险行动，从而造成事态均衡结果具有更大的不确定性。因此，反恐中需要加强情报工作从而准确研判暴恐分子心理状态。

恐怖事件；等级依赖期望效用模型；情绪；政府和恐怖分子；悲观和乐观

1 引言

当前恐怖主义成为各国政府和学术界关注的热点问题。澳大利亚智库“经济与和平研究所”(Institute for Economics and Peace)最新公布的统计数据显示，2013年全球范围内发生的恐怖袭击事件达到了1万起，较2000年1500起增加了数倍[1]。近几年亚洲成为恐怖分子袭击高发地。从近几年恐怖袭击的态势来看，恐怖组织手法越来越多样化，“基地”和IS等恐怖组织呈现网络发展趋势，恐怖组织的战略思维能力和协同执行能力不断上升，袭击目标从政府机关和标志性建筑转向普通民众。如何有效地开展反恐斗争已是各国政府亟待解决的问题。

关于反恐问题博弈分析的现有文献中，主要是针对政府反恐策略和恐怖分子策略进行研究，比如，恐怖分子的社会网络分析[2-3]，反恐资源调度优化[4-6]，恐怖主义产生的社会经济根源[7]，政府预警措施的优化策略[8]。上述文献均在传统博弈的分析框架下，恐怖分子与政府反恐力量均为完全理性的参与者，尚未考虑到恐怖分子的非理性行为，以及博弈双方存在的认知差异[9]。近十年来，博弈论基础理论围绕着参与者有限理性和非理性的基本假设加以扩展，涌现了一些新兴的分支领域。其中，Quiggin提出的等级依赖期望效用(Rank-Dependent Expected Utility, 简记为RDEU)[10]扩展了经典的期望效用理论。经典的Von Neumann 和Morgenstern期望效用理论(Expected Utility Theory)该理论假设概率是线性的，即满足独立性原则[11]。但是，阿莱悖论等大量实验经济学研究发现[12]，期望效用理论的基本假设与现实中决策行为并不完全一致，传统的期望效应理论并不能刻画在不确定条件下(比如情绪因素)参与者对风险和收益满足程度。等级依赖期望效用模型考虑了参与者的情绪(悲观、乐观)对风险和收益影响，认为决策的权重不仅仅依赖于局中人已知每种结果的概率，还应依赖于局中人对这些结果的情绪因素[13]。一些学者运用等级依赖期望效用理论分析了经典的鹰鸽博弈模型纳什解的存在性条件，显示了不同情绪类型的局中人博弈导致出现新的Nash均衡解[14]。考虑到突发事件中当事者较强的非理性情绪因素，一些学者分别运用等级依赖期望效用理论分析了情绪因素对于群体性突发事件的均衡结果影响[15-16]。

在世界各国恐怖袭击事件的防御与处置过程中，不仅恐怖分子存在着实施攻击前过于乐观的冒险行为、在世界各国严厉打击下转为悲观失望开始自首等各种情绪，各国反恐力量也不仅存在着对于反恐严峻性估计不足的过于乐观态度，而且还存在着面对各种新形态的恐怖主义蔓延和肆虐出现了“新悲观主义”的焦虑和惶恐情绪[17]。本文首先在传统博弈框架下建立了政府反恐力量和恐怖分子的博弈模型并分析混合Nash均衡；然后分别考虑了双方不同情境下的情绪因素，即单方或者双方，悲观或者乐观，对于恐怖袭击博弈的均衡结果影响。本文研究表明，政府反恐力量和恐怖分子的情绪因素对于暴恐事件双方的决策行为产生复杂而重大的影响。反恐斗争中政府反恐力量需要加强情报搜集、信息分析工作，准确把握暴恐分子的心理状态，从而制定出最优的防御/打击决策。

2 等级依赖期望效用理论

根据Quiggin[10]的等级依赖期望效用理论，本文给出如下定义。

定义1：对于随机变量X={xi;i=1,2,…,n}，X取xi的概率P{X=xi}=pi，对各个xi排序并规定x1>x2>…>xn，定义xi的效用等级(Rank position)记为RPi，作为其分布函数：

RPi=P{X≤xi}=pi+pi+1,i=1,2,…,n

(1)

直观上，xi的等级越高，不超过xi发生的概率就越大，xi在决策中占的权重就越大。

定义2：等级依赖期望效用模型是指偏好序“≻”可以用由效用函数u和情绪函数ω定义的实值函数V来表示，即对随机变量X、Y，有：X≻Y⟺V(X,u,ω) ≻V(Y,u,ω)[12]。在一个风险结构{p1,x1,…,pn,xn}中，等级依赖期望效用模型表示为：

π(xi)=ω(p1+p2+…+pi)-ω(p1+p2+…+pi-1)

(2)

根据(1)和(2)式，可以得到：

π(xi)=ω(pi+1-RPi)-ω(1-RPi)

(3)

其中，π(xi)是决定权重的函数，其中π(x1)=ω(p1)，情绪函数ω(·)满足ω(0)=0，ω(1)=1的单调增函数。当且仅当ω是凸函数时，π(xi)关于效用等级RPi是单调递减的；当且仅当ω是凹函数时，π(xi)关于效用等级RPi是单调递增的。

3 考虑情绪因素反恐博弈的等级依赖期望效用模型

3.1恐怖分子与政府反恐力量的传统博弈模型

考虑恐怖分子与恐怖反恐力量同时行动(或者先后行动但是彼此观察不到)问题，本文建立了表1所示的反恐问题传统博弈模型。其中，c1表示政府防御的成本，c2表示恐怖分子袭击的成本。a表示政府防御的收益，一般来说，a>c1。f表示政府反恐力量进行有效防御后恐怖分子遭受的损失。e表示恐怖分子袭击成功后获得的收益，一般来说，e>c2，f>e。b表示政府遭受恐怖袭击造成的损失，其绝对值大于政府防御的成本，b>c1。上述参数取值范围均为非负。

表1 恐怖分子与政府反恐力量的传统博弈模型

上述传统博弈模型仅存在着唯一的混合策略纳什均衡解，即政府反恐力量与暴恐分子均以一定的概率进行防御或发动暴恐袭击。由于整个社会完全转入反恐战争的战时状态需要付出高昂的成本代价，因此政府反恐力量仅能以一定的概率有选择性地采取机动灵活的防御措施。另一方面，暴恐分子在政府和整个社会的严厉打击下转换袭击的手段和目标，甚至可能转入潜伏状态。此时，混合均衡结果意味着反恐斗争面临着“猫捉老鼠”的长期化和复杂性趋势。

假设政府采取防御的概率为p，其中p∈(0,1)，恐怖分子袭击的概率设为q，q∈(0,1)。根据收益函数可以计算混合策略Nash均衡解的均衡概率为：

p*=(e-c2)/(e+f),q*=c1/(a+b)

在世界各国恐怖袭击事件的防御与处置过程中，由于事态的突发性和震撼性，恐怖分子和政府反恐力量双方均可能存在着较为强烈的乐观或者悲观情绪。例如，911事件后十余年内“基地”组织没有成功在美国本土进行恐怖主义活动、2011年美国成功击毙本拉丹、美国实施阿富汗撤军计划等事件反映了美国对于持续十余年反恐战争的乐观情绪。但是，2015年法国巴黎连环恐怖袭击事件凸显了国际反恐形势依然严峻，反恐斗争面临着长期化、复杂化和艰巨化，一些学者和机构对于完全消除恐怖主义深感悲观[17]。显然，上述乐观或悲观情绪直接导致政府部门选择了不同的反恐策略。

为了从理论上进一步剖析恐怖分子和政府反恐力量双方情绪因素对于事态发展结果的影响，本文运用等级依赖期望效用理论，扩展了双方的效用函数形式。不同的情绪因素将对参与者关于事件发生的主观概率造成一定的偏差，其中，对于乐观情绪将赋予事件更大的发生概率，对于悲观情绪将赋予事件较低的发生概率。因此，受到情绪因素影响的主观概率函数表示为：ω(pi)=pir，其中，pi为事件xi发生的客观概率，pi∈[0,1]。根据客观概率的取值范围，当ri=1时，局中人不带有情绪；当ri<1时主观高估了发生概率，称其为“乐观”情绪。根据(2)式可知，该事件在效用函数中所占权重将降低；当ri>1时主观低估了发生概率，称其为“悲观”情绪。同理，该事件在效用函数中所占权重将上升。具体如图1所示，图中纵轴表示概率累计分布，即情绪函数ω；凹曲线表示悲观情绪下将低估事件的发生概率。对于事件xi，悲观情绪下其在效用函数中所占权重π(xi)将大于中性(不带有情绪)情境下所占权重△pi。

图1 悲观情绪下事件xi在效用函数中所占权重的示意图

3.2恐怖分子与政府的等级依赖期望效用模型

根据表1所示的传统博弈支付矩阵，可以得出政府反恐力量采取各种策略获得的效用按照从大到小排序：a-c1>0>-c1>-b，即效用等级或者秩位。根据定义(1)、(2)和(3)，可以分别计算出政府反恐力量的效用等级和决策权重，具体如表2所示。

表2 考虑情绪的政府等级依赖期望效用

根据公式(2)，得出政府反恐力量的等级依赖期望效用模型：

Vg=(a-c1)(pq)r1+(b-c1)(1-q+pq)r1+c1(1-p-q+2pq)r1-b

(4)

同理，根据表1传统博弈的支付矩阵，得出恐怖分子采取各种策略获得效用的从大到小排列：e-c2>0>-f-c2。

恐怖分子的等级依赖期望效用模型：

Va=(e-c2)(q-pq)r2+(-f-c2)[1-(1-pq)r2]

(5)

表3 考虑情绪的恐怖分子等级依赖期望效用

4 情绪因素对于反恐博弈均衡影响

根据考虑情绪因素的等级依赖效用函数(4)和(5)，分别对双方行动概率p和q求偏导并令偏导为0，纳什均衡解的存在性取决于该方程组解的存在性：

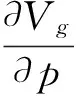
(6)

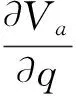
(7)

4.1情境1：恐怖分子处于乐观或悲观情绪

当政府反恐力量处于冷静研判并准确预期的状态时，r1=1。但是，暴恐分子在宗教极端思潮的裹挟下，其对于袭击行动处于狂热的过度乐观情绪；或者在政府反恐力量的强大震慑下开始悲观失望，即r2≠1。分析该种情境下恐怖分子情绪因素对于表1传统博弈均衡结果的影响。

首先，将r1=1代入政府反恐力量的等级依赖期望效用(6)式，可得恐怖分子袭击的均衡概率：q*=c1/(a+b)。

其次，把q*=c1/(a+b)代入恐怖分子的等级依赖期望效用(7)式，得到：

(8)

通过求解上述方程，可以得到政府反恐力量的混合策略Nash均衡解p*。

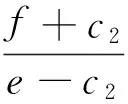
(9)

(10)

分析该结果，当政府处于冷静研判状态并被恐怖分子感知时，暴恐分子的最优袭击策略不变。但是，当暴恐分子存在着情绪因素后，或者在极端宗教思潮裹挟下产生乐观情绪，或者在政府严厉打击下产生悲观情绪，政府反恐力量正确捕捉到这一信息后，政府将改变原先的最优反恐决策。因此，政府反恐力量需要加大情报搜集，准确研判暴恐分子的心理状态，进而制定最优的反恐决策。

4.2情境2：政府反恐力量处于乐观或悲观情绪

此时恐怖分子能够做出准确的预期，即r2=1。但是，政府反恐力量对于反恐态势做出了错误的判断，或者处于盲目乐观的情绪中(例如911事件后美国推行单边主义反恐政策，发起了两场反恐战争)，或者陷入了悲观情绪，即r1≠1。分析该种情景的均衡解。

首先，将r2=1,代入恐怖分子的等级依赖期望效用(7)，可得政府反恐力量的均衡概率：p*=(e-c2)/(e+f)。由收益限制条件e>c2和f>e，可知p*=(e-c2)/(e+f)<1/2。

其次，把p*=(e-c2)/(e+f)代入政府反恐力量的等级依赖期望效用(6)，得到：

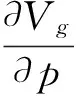
(11)

可以证明，通过求解上述方程，可以得到恐怖分子的Nash均衡解q*。

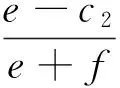
(12)

对(12)式求导，可得：

(13)

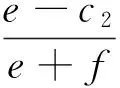
结论1：在考虑情绪因素的政府和恐怖分子的博弈过程中，如果一方处于冷静研判并准确预期的状态，另一方行动处于过度乐观(悲观)的情绪情境下，博弈的原混合策略Nash均衡将发生改变：

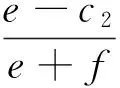
(3)如果政府处于过度乐观(悲观)的情绪情境，恐怖分子处于冷静研判并准确预期的状态(r1≠1，r2=1)，并且当恐怖分子袭击的概率大于或等于0.5(q≥0.5)时，政府反恐力量的过分反应将造成其行动收敛到防御策略，考虑情绪因素的反恐博弈模型原混合均衡结果转化为纯策略纳什均衡结果(防御，不袭击)。

4.3情境3：恐怖分子和政府反恐力量都处于乐观或悲观的情绪

在恐怖袭击事件中，政府反恐力量和恐怖分子双方都有可能处于极端情绪中，从而导致了对于事态的判断出现过度乐观(或者悲观)的偏差，即r1≠1且r2≠1。此时，若存在p,q的值使(6)和(7)成立，则说明考虑情绪因素下反恐博弈仍存在混合策略Nash均衡解。

证明：分析政府反恐力量均衡策略p*的存在条件。为了判断公式(7)的连续性，设右端为函数f(p)=(e-c2)(1-p)r2q(r2-1)-(f+c2)(1-pq)(r2-1)p，求导：

(14)

由此可知公式(7)为p的单调递减函数。

考虑到如下边界值：

根据中值定理，可知(0，1)之间存在p=p*(r2,q),使得(7)式∂Va/∂q=0成立。所以，考虑恐怖分子和政府反恐力量双方情绪因素的反恐博弈模型中，政府反恐力量的防御策略存在着唯一的混合策略Nash均衡解p=p*(r2,q)。

同理，分析恐怖分子均衡策略q*的存在条件。为了判断公式(6)的连续性，设右端为函数g(q)=q(a-c1)(pq)(r1-1)+q(b-c1)(1-q+pq)(r1-1)+c1(2q-1)(1-p-q+2pq)(r1-1)，求导：

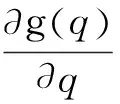
在上式右端中，前两项均大于零，分析第三项取值范围。由于(2p-1)(2q-1)∈[-1,1]，(1-p-q+2pq)∈[0,1]，因此第三项也大于零，即∂g(q)/∂q>0。由此可知公式(6)为q的单调递增函数。

考虑如下边界值：

根据中值定理，可知(0，1)之间存在q=q*(r1,p)，使得(6)式∂Vg/∂p=0成立。所以，考虑恐怖分子和政府反恐力量双方情绪因素的反恐博弈模型中，恐怖分子的袭击策略存在着唯一的混合策略Nash均衡解q=q*(r1,p)。

结论2：考虑情绪因素的政府反恐力量和恐怖分子博弈模型中，两个局中人都处于情绪的状态情况下，存在着唯一的混合策略Nash均衡解(p*(r2,q)，q*(r1,p))。

为了更加直观地阐释结论2的混合策略Nash均衡结果，下一节将结合我国新疆6.28暴恐事件的案例(该案例参见文献18)，给出相应的数值分析。

5 数值分析：以新疆6.28暴恐事件为例

5.1事件回顾及收益值假设

2014年6月28日中午，新疆维吾尔自治区南部和田地区发生严重的暴力恐怖袭击事件，墨玉县警方立即启动应急反应机制平息事态，并对嫌犯展开搜捕行动[19]。据《新疆日报》报道[20]，墨玉县7个乡镇180个村自发参与围捕的群众达3万人以上，共同联手摧毁暴恐团伙。自治区决定拿出3亿余元奖励所有参与近期围捕专项行动的群众及相关人员。先期对和田地区违捕专项行动中涌现出的先进集体和先进个人进行表彰奖励，金额达423万元。

由于恐怖袭击事件具有无法重现性、社会敏感性和突发性，难以获取相应数据，国内外研究文献在理论建模分析基础上，普遍采取了社会仿真分析和数值分析方法[5,6,8]。结合新疆6.28暴恐事件的案例，确定表1中博弈模型收益值。其中，一些数据难以准确度量，但是作为数值分析的参考，并不影响收益函数的基本性质和主要结论。

首先，假设有效遏制暴恐事件多发态势的反恐收益可视为地方社会经济稳定发展的红利。根据墨玉县人民政府办公室发布的信息，随着县域经济的加速发展，2013年墨玉县GDP增长3.95亿元，即a=39500万元。同理，恐怖分子发动袭击成功将会导致公共安全和社会资源财富的损失，即b=39500万元。考虑到反恐投入，除了先期奖励423万元以外，3万余群众自发参与到围剿行动中，根据2013年新疆地区最低日工资标准121.6元， 3万人参与围捕专项行动的经济成本可设定为364.8万元，因此，“6.28”暴恐事件当地直接的反恐投投入为c1=364.8+423=787.8万元。

其次，根据联合国发表一份报告，2001年9·11恐怖袭击后，恐怖分子在制造任何一次大的恐怖袭击时，成本都没有超过5万美元[21]。这些恐怖袭击包括巴厘岛爆炸案、马德里爆炸案及伊斯坦布尔大爆炸等。考虑2014年6月人民币对美元平均汇率6.15，不妨将恐怖分子发动袭击的成本设为c2=5×6.15=30.75万元。

第三，我国修改后的《刑事诉讼法》增设违法所得特别没收程序，对于恐怖活动犯罪等重大犯罪案件，犯罪嫌疑人、被告人潜逃或者死亡，应追缴其违法所得及其他涉案财产。根据《中国民生发展报告2014》，2012年全国家庭净财产均值为43.9万元[22]。所以，假设恐怖分子发动袭击行动失败需要付出的代价为f=43.9万元。

第四，2013年新疆维吾尔自治区本级公共安全支出52.9亿元，自治区财政还对各市、州、地区另外转移支付了45.7亿元的公共安全经费，两项合计为98.6亿元，同比增长了5.6%。恐怖分子实施暴力袭击活动的目的即是扰乱社会秩序，破坏民族团结，意在达成宗教、政治或意识形态上的意图。其发动袭击对公共安全造成的影响虽然无法准确统计，但可以通过每年各地方(新疆现有88个县或县级市)用于公共安全的经费支出进行推算。结合上面的数据，可以得出如果恐怖分子在墨玉县发动袭击成功，那么可以设定他们获得的收益为e = 986000×(1+5.6%)/88=11832万元。

上述收益值满足表1中混合均衡的存在条件：p*=(e-c2)/(e+f)=0.9937,q*=c1/(a+b)=0.00997。由于新疆“6.28”案例中参数值相差三个数量级，该混合均衡结果取值接近于纯策略{防御，不袭击}均衡结果(p*=1,q*=0)。

5.2数值分析结果

将上述数值代入(6)(7)式，得到：

∂Vg/∂p=r1[38712.2q(pq)(r1-1)+38712.2q(1-q+pq)(r1-1)+787.8(2q-1)(1-p-q+2pq)(r1-1)]=0

(15)

∂Va/∂q=r2[11801.25(1-p)r2q(r2-1)-74.65(1-pq)(r2-1)p]=0

(16)

图2 双方持有乐观情绪的混合均衡

图3 双方持有悲观情绪的混合均衡

若(15)、(16)式存在等于零的解，则Nash均衡存在，判断即两个函数是否存在着交点或者具有多个交点。相应数值结果如图2-5所示。由于案例中有关参数的数量级相差较大，因此图中横轴政府防御的均衡概率普遍较大(接近于无情绪时均衡值p*= 0.9937)。

分析图2，随着政府反恐力量的乐观情绪增大(r1减小)，将诱导暴恐分子采取更大的袭击概率(袭击策略的混合均衡q*增大)；但是随着暴恐分子乐观情绪的增大(r2减小)，政府反恐力量将倾向于增大防御(防御策略的混合均衡概率p*增大)。在图3中，随着暴恐分子悲观情绪的上升(r2增大)，政府防御策略的均衡概率下降；但是当政府反恐力量悲观情绪上升时(r1增大)，暴恐分子的袭击概率略微增大。

图4 政府乐观和恐怖分子悲观的混合均衡

图5 恐怖分子乐观和政府悲观的混合均衡

在图4中，随着政府反恐力量的乐观情绪增大(r1减小)，将诱导暴恐分子采取更大的袭击概率(袭击策略的混合均衡q*增大)；但是随着暴恐分子悲观情绪的增大(r2增大)，政府反恐力量将相应地减少防御(防御策略的混合均衡概率p*变小)。在图5中，随着政府反恐力量悲观情绪的上升(r1增大)，暴恐分子的袭击概率略微增大；随着暴恐分子乐观情绪的增大(r2减小)，政府防御的均衡概率p*也将相应地增大。

尽管由于新疆“6.28”案例中有关参数存在着数量级差异，但是上述结果仍然反映了结论2，即任何一方存在着对事态发展的悲观/乐观情绪时，势必影响到另一方的均衡策略选择。基本上，当暴恐分子对于事态研判为悲观情绪时，政府反恐力量将在混合均衡中减少防御策略的概率；当暴恐分子对于事态发展具有乐观情绪时，政府反恐力量将不得不增大防御策略的概率。

6 结语

恐怖袭击具有袭击者有暴力恐怖，目标多元化，宗教色彩等一系列非理性、时间紧迫的极端约束条件的非常规特征。除了常规前向归纳推理、有限理性博弈模型等的不同角度外，本文从当事双方对于事态发生主观概率存在着乐观或悲观情绪的角度提供了一种新阐述。在恐怖袭击事件实施和应急处置过程中，政府反恐力量和恐怖分子的心理可能随着态势变化出现情绪波动，双方非理性的情绪因素对其决策和执行过程都会产生行为偏差。

本文运用期望等级依赖效用理论，分析了政府反恐力量和暴恐分子的乐观/悲观情绪对于博弈均衡结果的影响。研究表明：如果一方处于冷静研判并准确预期的状态，另一方行动处于过度乐观(悲观)的情绪情境下，博弈的原混合策略Nash均衡将发生改变。其中，当恐怖分子袭击的概率较大，同时政府处于悲观情绪、恐怖分子处于准确预期的状态时，相对于政府的乐观情绪，原混合均衡结果将以更快速度转化为纯策略纳什均衡结果(防御，不袭击)。当双方都存在情绪因素情境下，任何一方存在着对事态发展的悲观/乐观情绪时，势必影响到另一方的均衡策略选择。其中，当暴恐分子对于事态研判为悲观情绪时，政府反恐力量将在混合均衡中减少防御策略的概率；当暴恐分子对于事态发展具有乐观情绪时，政府反恐力量将不得不增大防御策略的概率。因为存在着乐观情绪的恐怖分子其更加易于冒险采取袭击行动，从而造成事态均衡结果更大的不确定性。

本文的研究结果表明，在开展反恐斗争、制定应急预案的过程中，政府反恐力量需要准确把握暴恐事件的态势，一方面避免自身做出过于盲目乐观的判断造成不必要损失，另一方面需要从战术上高度重视敌人，把形势估计得更严重一些、问题想得更困难一些，从而有利于加大防御发挥出不战而屈人之兵的反恐震慑效果。同时，政府反恐力量需要尽可能捕捉和把握暴恐分子的心理状态，从而制定出最优的防御/打击决策。因此，加强情报搜集、信息分析工作[23]，是反恐斗争中的一个关键环节。

[1] 王芳菲. 全球2013年恐怖袭击达1万起，非洲亚洲最多[EBOL]. [2014-11-20]. http://www.hnr.cn/news/kx/201411/t20141120_1715564.html.

[2] 付举磊, 孙多勇, 肖进, 等. 基于社会网络分析理论的恐怖组织网络研究综述[J]. 系统工程理论与实践, 2013, 33(9): 2177-2186.

[3] Ressler S. Social network analysis as an approach to combat terrorism: Past, present, and future research[J]. Homeland Security Affairs, 2006, 2(2): 1-10.

[4] 韩传峰,孟令鹏,张超,等.基于完全信息动态博弈的反恐设施选址模型[J].系统工程理论与实践,2012, 32 (2):366-372.

[5] 柴瑞瑞, 孙康, 陈静锋, 等. 连续恐怖袭击下反恐设施选址与资源调度优化模型及其应用[J]. 系统工程理论与实践, 2016, 36(2): 464-472.

[6] Nikoofal M E, Zhuang Jun. On the value of exposure and secrecy of defense system: First-mover advantage vs. robustness[J]. European Journal of Operational Research, 2015, 246(1): 320-330.

[7] Sandler T, Enders W. An economic perspective on transnational terrorism[J]. European Journal of Political Economy, 2004, 302(20): 301-316.

[8] Pinker J E. An analysis of short-term responses to threats of terrorism[J]. Management Science, 2007, 53(6): 865-80

[9] 刘德海, 周婷婷. 基于认知差异的恐怖主义袭击误对策分析[J].系统工程理论与实践, 2015, 35(10): 2646-2655.

[10] Quiggin J. A theory of anticipated utility[J]. Journal of Economic Behavior and Organization, 1982, 3(4): 323-343.

[11] Von Neumann J, Morgenstern O. Theory of games and economics behavior[M]. Princeton: Princeton University Press, 1944.

[12] Allais M. Extension of the theories of general economic equilibrium and social output to the case of risk[J]. Econometric, 1953, 2(4): 503-546.

[13] Enrico D, Wakker P P. On the intuition of rank-dependent utility[J]. The journal of risk and uncertainty, 2001, 23(3): 281-298.

[14] 龚日朝. 基于秩依期望效用理论的鹰鸽模型博弈均衡分析[J]. 管理科学学报, 2012, 15(9): 35-44.

[15] 熊国强, 张婷, 王海涛. 情绪影响下群体性冲突的RDEU博弈模型分析[J]. 中国管理科学, 2015, 23(9): 162-170.

[16] 方乐，张松，周婷婷，等. 考虑情绪因素的群体性突发事件等级依赖期望效用模型[J].电子科技大学学报(社会科学版), 2015, 17(2): 34-40.

[17] 赵可金.反恐十年的美国与世界[N]. 学习时报，2011年9月12日,第2版.

[18] 刘德海, 韩呈军. 基于心智模型的恐怖主义袭击扩展式演化博弈分析[C]. 第十三届全国青年管理科学与系统科学学术会议, 2015年10月17日, 西安.

[19] 邱永峥, 王盼盼. 新疆和田发生恐怖袭击事件[N]. 环球时报, 2013-6-29, 第4版.

[20] 张昕宇等. 筑起打击暴恐犯罪的铜墙铁壁：自治区重奖围捕暴徒的群众引起强烈反响[N]. 新疆日报, 2014年8月6日，第3版.

[21] 刘媛. 据称恐怖分子袭击伦敦地铁成本低廉仅两千美元[EBOL].[2006-01-04]. http://news.xinhuanet.com/world/2006-01/04/content_4006760.htm

[22] 谢宇, 张晓波, 李建新, 等. 中国民生发展报告2014[M]. 北京：北京大学出版社，2014.

[23] 刘德海. 信息交流在群体性突发事件处理中作用的博弈分析[J]. 中国管理科学, 2005, 13(3): 95-102.

HowdoesthePessimisticorOptimisticEmotionInfluencetheGameEquilibriumOutcomeinIncidentsofViolenceandTerrorism

LIUDe-hai1,2，BAOXue-yan2，WANGXie-ning1

(1．School of Management science and Engineering, Dongbei University of Finance & Economics, Dalian 116025,China；2. Center of Econometric Analysis and Forecasting, Dongbei University of Finance & Economics, Dalian 116025,China)

Terrorist’s attack has become a severe challenge for human society. Both terrorists and government anti-terrorist force possess the obvious characteristics of scenario-dependent decision and irrational emotion decision. For example, the player with the optimistic emotion usually overestimates the probability of the event, and the player with the pessimistic emotion usually underestimates the probability of the event. Obviously, it has important influence on the optimal decision and equilibrium results.

1003-207(2017)10-0080-09

10.16381/j.cnki.issn1003-207x.2017.10.009

C931

A

2016-05-10；

2017-02-21

国家自然科学基金资助项目(71271045, 71571033，71503033, 71602021)；东北财经大学学科建设支持计划特色学科项目(XKT-201411)

刘德海(1974-)，男(汉族)，辽宁辽阳人，东北财经大学管理科学与工程学院教授、博导，研究方向：突发事件应急管理，E-mail：Ldhai2001@163.com.

And then, the effect of emotion on the equilibrium outcomes of the traditional government-terrorist game model is discussed, where governmental anti-terrorist force or terrorist has an optimistic or pessimistic expectation on the subjective probability about terror attack. Taken by the method of case analysis, the special scenario that both two parties have an optimistic or pessimistic emotion based on Xinjiang 6.28 terrorist incident in Moyu County is further discussed. Lastly, the paper discusses the management meaning on improving anti-terrorist strategy.

The results show that when any one player has an optimistic or pessimistic expectation, the opponent without any emotion should adjust his/her equilibrium probability. That is to say, any party’s emotion should influence the opponent’s strategy selection. When both two parties have the emotional factor, the terrorist with optimistic expectation should be more inclined to take excessive risk, which causes the equilibrium outcome has the more uncertainty.

The paper’s results are useful for the anti-terrorism and emergency plans. First, the government should avoid the short-sighted optimism in order to reduce the unnecessary loss. Second, the government should come to a more serious appraisal of the situation and think of more difficulties, because a stronger defense can banish every attack thought. Third, the government should strengthen the intelligence collecting and information analysis. Thus, anti-terrorism need to strengthen intelligence for accurately judging terrorist’s psychological states.

Keywords： terror attack; Rank-Dependent Expected Utility theory; emotion; government and terrorist; pessimism and optimism