轴流压气机特性计算及激波模型研究

蒋筑宇，范召林，刘 波

轴流压气机特性计算及激波模型研究

蒋筑宇1，范召林1，刘 波2

（1.中国空气动力研究与发展中心，四川绵阳621000；2.西北工业大学动力与能源学院，西安710072）

为快速准确预估轴流压气机特性和激波损失，基于轴流压气机S2流面流线曲率法，分别采用正激波模型和改进的双激波模型，对某型2级跨声速风扇特性进行数值模拟计算，得到了1 00%设计转速近设计点与99.76%设计转速近堵塞点的总体性能和气动参数，以及95%、1 00%和1 1 0%设计转速的特性曲线。通过将计算结果与试验数据进行对比，分析研究了各激波损失模型在激波损失预估和风扇/压气机特性计算方面的差异。分析结果表明：在跨声速风扇/压气机近设计点激波损失和特性参数的计算中，正激波模型损失径向分布计算结果接近试验值，总压比和总效率计算值分别较试验值约低1.96%和2.54%，模型能够满足工程需要。而在近堵塞点，改进的双激波模型总损失计算值更接近试验值，总压比计算值和试验值很吻合，总效率计算值比试验值约高7.28%。改进双激波模型的不同转速线效率特性曲线也明显更接近试验值，模型能够较准确地预测远离设计点激波损失和特性参数。

轴流压气机；流线曲率法；激波模型；损失预估；特性计算

0 引言

全3维数值模拟技术已经取得了很大进展。利用基于雷诺平均的可压缩非定常Navier-Stokes方程求解叶轮机械内部流动可以得到详细的流场信息，特性预估可信度高；但受湍流模型、转捩模型和网格数量等限制，模型建立复杂，计算量大，主要用于验证计算[1-3]。而基于叶轮机械准3维流动通用理论的S2流面通流设计，运算效率更高，时间成本更低，目前仍然是叶轮机械设计体系的核心。Novak提出的流线曲率法[4]是1种数学上相对简单，使用经验较丰富，应用较成熟，计算参数也较准确的S2流面求解方法[5]。流线曲率法数学模型基于无黏假设，对压气机气动损失的预估主要依赖于损失模型。

对于级负荷不高、相对马赫数较低的风扇/压气机来说，20世纪60年代初Miller等发展的2维通道正激波模型就能较成功地预测激波损失[6-7]；而对于现代高负荷压气机，在实际叶栅流动中，随着来流马赫数的提高，激波和附面层相互作用加强，激波的形状和结构会发生很大变化，正激波模型对激波损失的预估误差随之变大，用流线曲率法预测非设计工况激波损失前，必须知道激波的结构和波前马赫数才能比较准确地建立起激波损失模型[8]。Bloch的研究表明，在跨声速风扇转子叶尖，激波结构主要为叶栅入口斜激波和通道正激波，并会随工作状态的变化而变化[9-10]；Biollo的研究也得到了相似的结果[11]；Boyer在Bloch等研究的基础上，考虑到来流攻角对激波结构的影响，提出了双激波模型[10]。

本文利用流线曲率管流计算方法[12]，结合损失和落后角模型，并在双激波模型基础上改进，开发了1套完整的轴流压气机损失预估和特性计算方法。参考NASA公开发表的试验数据[13-14]，利用程序对某型2级高负荷跨声速风扇进行了数值模拟，得到了近设计点和近堵塞点的总体性能参数和展向参数分布，以及全工况的特性曲线。通过与试验结果对比，重点研究了正激波和改进的双激波模型在轴流压气机损失预估和特性计算中的效果和差异。

1 数值方法

计算对流场做出了定常、绝热、无黏和轴对称的假设，气体黏性对级作功能力和流道面积的影响用流道堵塞系数来改进。主要控制方程为计算站沿径向的完全径向平衡方程和连续方程。

2 攻角和落后角模型

2.1 攻角模型

参考Lieblein和Johnsen等基于NACA-65-A10系列低速叶型试验数据建立的经验关系式计算参考攻角i*[15]，即最小损失攻角imin。利用Herrig提出的有效范围攻角公式计算近堵塞攻角ichoke和近失速攻角i stall[16-17]。

2.2 落后角模型

与参考攻角一样，参考落后角也选为最小损失落后角，参考Lieblein提出的经验模型[15]计算参考落后角δ*。以Hearsey和Boyer模型分量组合方法为基础展开[10]，非设计点落后角

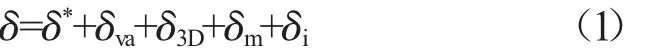
式中：δva为轴向速度比对落后角的影响；δ3D为压气机中流线在不同展向位置对落后角的影响；δm为马赫数变化对落后角的影响，在跨声速转子流动后，马赫数对落后角影响很小，可以忽略；δi为非设计状态下攻角变化对落后角的影响。

3 总压损失模型

本文考虑的跨声速风扇/压气机叶片排通道总压损失主要包括由黏性引起的叶片附面层叶型损失和气流穿越无黏激波所引起的激波损失。

3.1 叶型损失模型

考虑二次流、端壁损失以及激波与附面层干扰所引起的叶顶及叶根附加损失，采用Hearsey和Boyer的方法计算附加损失]。

3.2 激波损失模型

3.2.1 正激波模型

正激波模型将叶栅通道激波简化为1道在通道入口处与通道中线垂直的正激波。当来流相对马赫数Ma'1＞1时，激波前有效马赫数波Ma'e为

式中：Ma'B为叶型吸力面与激波交界点处的气流马赫数。当 Ma'1＜1 时，则

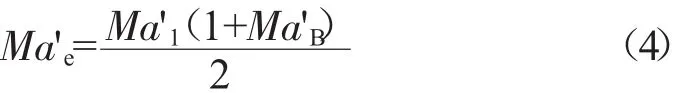
若 Ma'e＜1，则激波损失为 0；若 Ma'e＞1，由正激波关系式计算激波损失。

3.2.2 改进的双激波模型

在双激波模型中，激波结构随攻角变换有3个特征形态点，即近堵塞点（NC），峰值效率点（PE）和近失速点（NS），如图 1所示。

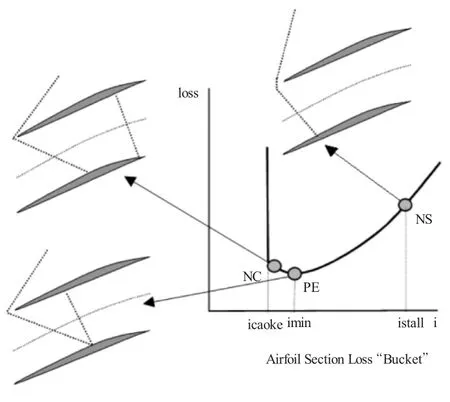
图1 双激波模型

当来流攻角i等于最小损失攻角imin时，通道入口斜激波波后马赫数即为通道正激波波前马赫数。由斜激波关系式计算气流通过斜激波损失。Boyer提出可将激波声速点激波角εsonic作为激波平均倾斜角，这也是目前的普遍处理方法[7,18]，εsonic由Bloch-Moeckel脱体激波模型方法求解[9]

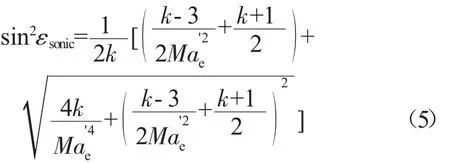
εsonic仅为马赫数的函数，采用εsonic作为激波角可以排除叶型前缘半径的影响，但这样会使斜激波波后马赫数降为1。对此，本文在正激波损失计算中引入波前修正马赫数Ma2e

若 Ma2e＞1，则计算正激波损失；若 Ma2e＜1，则不考虑正激波损失。

随着来流攻角i减小，通道激波向后移动，当攻角等于近堵塞攻角ichoke时，正激波后移至通道出口，将斜激波和正激波之间的流动假设为拉瓦尔喷管内的流动，由König提出的方法求出正激波前马赫数[19]。在接近堵塞状态时激波损失激增，对此，在i介于ichoke和imin之间时，激波损失利用函数 F（（i-imin）4）插值求得，如图2所示。

图2 攻角小于i min时激波损失函数

F（（i-imin）4）沿 i的变化趋势接近实际激波损失，但与试验结果的对比表明，在接近堵塞工况时损失计算值偏小，致使效率计算值偏大。对此，本文引入参数l（l＞1）将，损失函数改进为

改进函数仍然为i-imin的4次多项式函数。如图2所示，改进后，在接近堵塞状态时，激波损失更大；而在攻角较大时，损失基本与原函数值相同。

随着来流攻角i增大，通道激波向前移动，通道入口斜激波增强，将斜激波看作无限层排列的脱体弓型激波[10]。忽略来流马赫数通过每道斜激波的变化，气流经过所有激波后压比为[20]

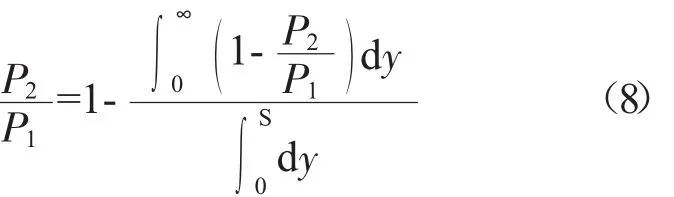
按斜激波理论计算脱体激波后马赫数，激波斜角ε 由函数 G（（i-imin）4）求得。

当攻角i＞inorm时，叶栅通道激波变为入口脱体正激波，激波损失计算方法与正激波模型一致。inorm由经验公式求得

4 计算结果及分析

本文研究对象为某2级跨声速风扇/压气机[13-14]，在设计状态下的总体性能参数为：总压比2.8，绝热效率83.9%，质量流量83.5 kg/s。设计转速为10720 r/min；进口条件为标准大气条件，轴向进气；静子出口轴向出气；第1级转子有减振凸台，叶型为多圆弧叶型。

4.1 设计点程序验证计算

采用文献[13]给出的风扇设计点各级损失和落后角，利用本文程序对设计点进行数值模拟，将计算得到的总体性能参数与设计值进行对比，以验证程序的有效性。设计点各级累积增压比和绝热效率的设计值和数值模拟结果对比见表1、2。

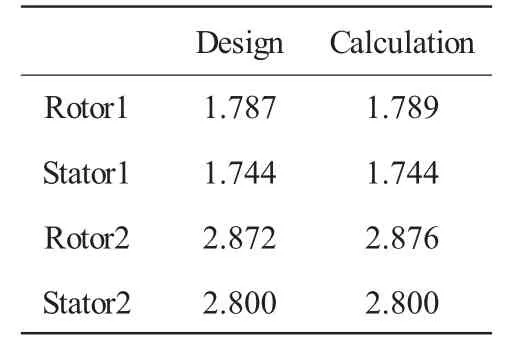
表1 设计点累积增压比设计值与计算值

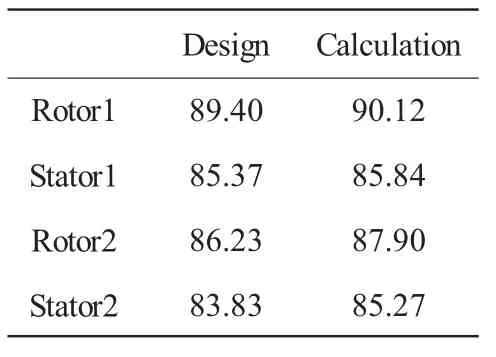
表2 设计点累积绝热效率设计值与计算值 %

从表中可见，设计点总体气动性能计算值跟设计值很接近。总增压比计算值跟设计值吻合很好，总绝热效率计算值比设计值略高，本文程序计算精度较高。

4.2 近设计点特性计算

分别结合2种激波模型和落后角模型，利用程序对风扇近设计点进行数值模拟计算，近设计点转速为100%设计转速，流量为83.574 kg/s。近设计点各级累积增压比和绝热效率的设计值和数值模拟结果对比见表 3、4。

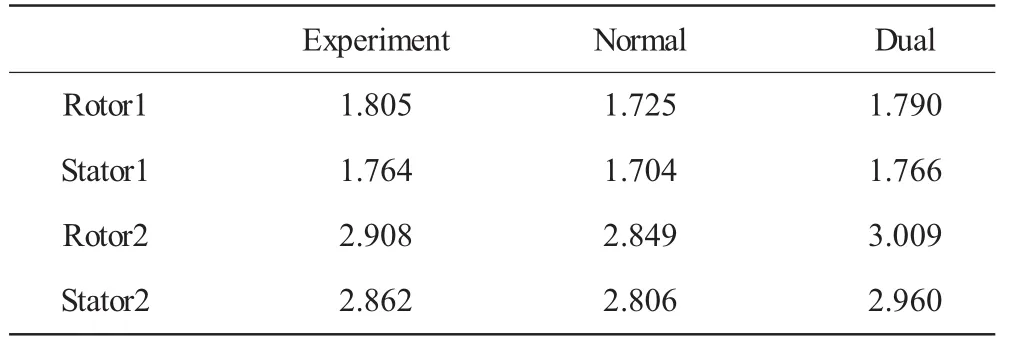
表3 近设计点累积增压比试验值与计算值

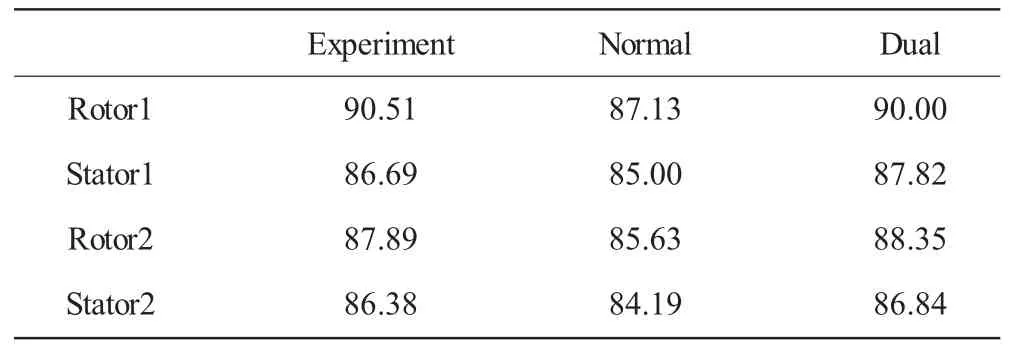
表4 近设计点绝热效率试验值与计算值 %

从表中数据可见，采用正激波模型计算得到的增压比和绝热效率均小于试验值，而双激波模型计算结果均大于试验值。正激波模型总压比的计算结果较试验值约低1.96%，总效率的计算结果较试验值约低2.54%。而双激波模型总压比的计算结果较试验值约高3.42%，总效率的计算结果较试验值约高0.53%。

各级转、静子损失试验值和计算值沿展向分布如图3、4所示。

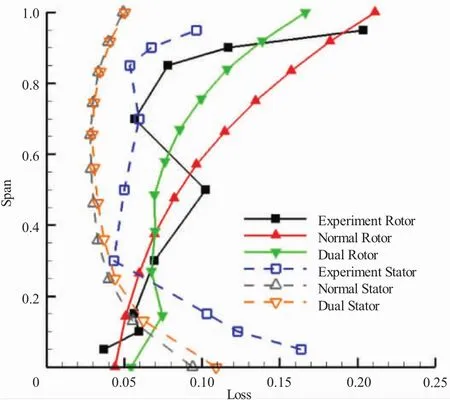
图3 第1级损失试验值与计算值

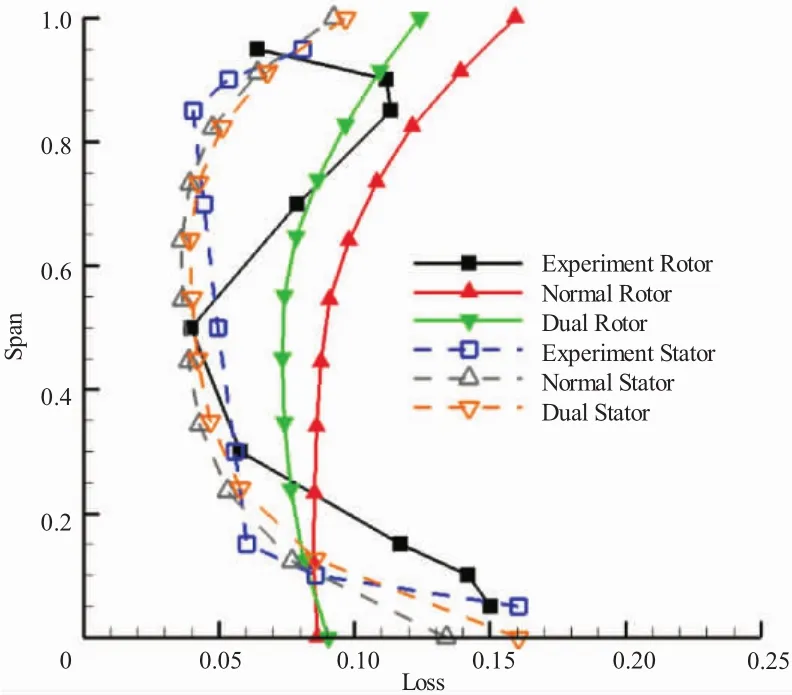
图4 第2级损失试验值与设计值

从图3中可见，第1级转子损失试验值沿展向总体呈增长趋势，受凸台的影响，转子叶中位置损失出现突增。第1级静子叶中部分损失试验值较小，叶尖和叶根部分较大。转子损失计算值大致反映出试验值变化趋势，静子损失计算值与试验值也比较接近。从图4中可见，第2级转子和静子损失试验值均表现为叶展中部相对较小，叶尖和叶根部分相对较大。转子叶根部分损失计算值较试验值偏低，而叶中到叶尖部分计算值与试验值较接近。静子损失计算值和试验值吻合很好。在2级转子全展向范围内，正激波模型损失计算结果基本高于双激波模型的，且沿展向差值增大。

各级绝热效率试验值和计算值沿展向分布如图5、6 所示。

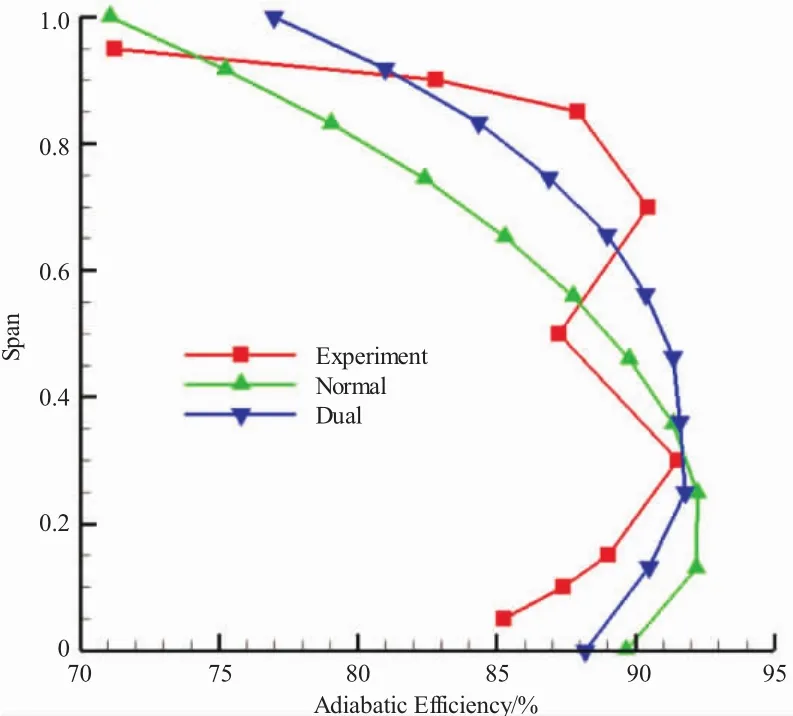
图5 第1级绝热效率试验值与计算值

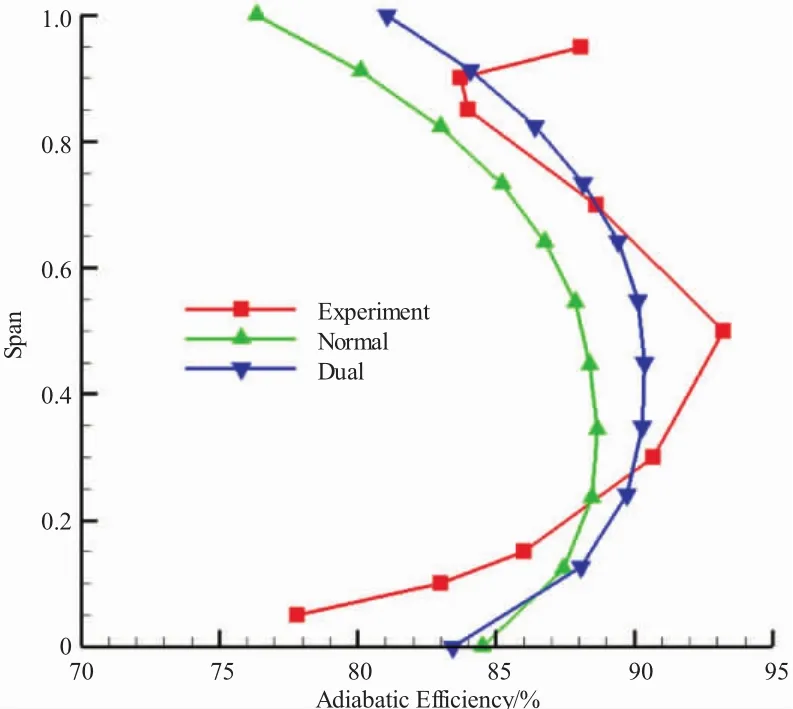
图6 第2级绝热效率试验值与计算值

从图5中可见，第1级绝热效率试验值总体上沿展向呈下降趋势，由于转子凸台使转子中部损失突增，叶展中部效率因此降低。绝热效率计算值较好反映了试验值变化趋势。从图6中可见，第2级绝热效率试验值叶展中部相对较高，叶尖和叶根部相对较低。效率计算值与试验值也较符合。对比损失图和绝热效率图可见，各级损失试验值沿展向变化趋势与效率试验值基本相反，说明级损失大小直接影响了级效率高低。由于正激波模型损失计算值更大，所以在2级全展向范围内，其效率计算结果基本低于双激波模型的，且沿展向差值增大。

各级转子出口相对气流角和静子出口气流角试验值和计算值沿展向分布如图7、8所示。

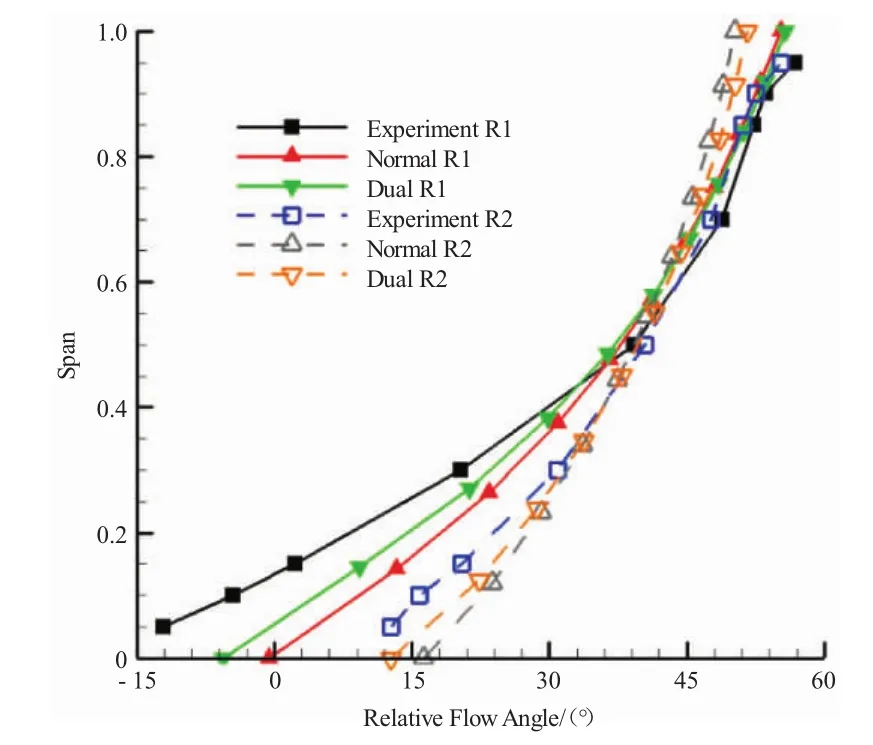
图7 转子出口相对气流角试验值与计算值

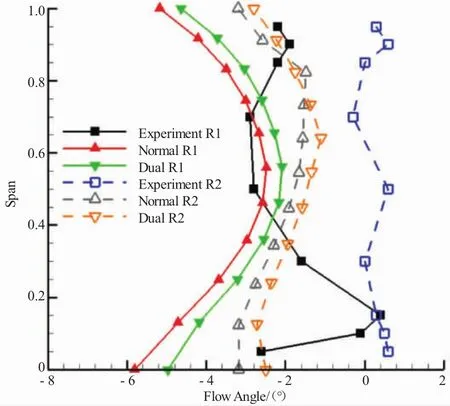
图8 静子出口气流角试验值与设计值

从图7中可见，2级转子出口相对气流角试验值沿展向逐渐增大，2级转子出口相对气流角计算值和试验值比较接近，转子根部计算值比试验值偏大。从图8中可见，第1级静子出口气流角试验值沿展向变化较曲折，第2级静子试验结果则基本呈轴向出气。第1级静子叶展中部出口气流角计算值和试验值比较接近，叶根和叶尖部分差异较大。第2级静子出气角计算值比试验值小。2级转子根部双激波模型出口相对气流角计算结果比正激波的大。2级静子各展向位置，双激波模型出口气流角计算值比正激波模型的高 0.5°左右。

综合来看，在近设计点损失预估和特性计算上，2种模型没有明显的优劣区别，正激波模型计算结果能够满足工程需求，采用该模型更简单有效。

4.3 近堵塞点特性计算

利用程序对近堵塞点进行数值模拟，近堵塞点转速为99.76%设计转速，流量为83.866 kg/s。近堵塞点级累积增压比和绝热效率试验值和数值模拟计算结果对比见表5、6。

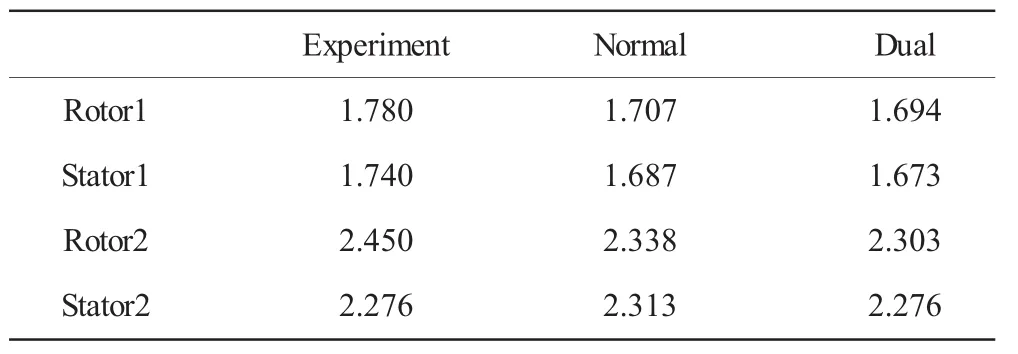
表5 近堵塞点累积增压比试验值与计算值

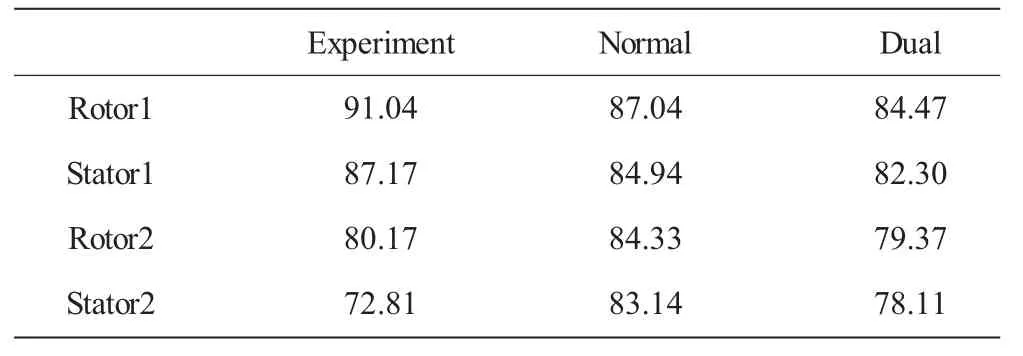
表6 近堵塞点累积绝热效率试验值与计算值 %

从表5、6中可见，相对于近设计点，近堵塞点总压比和总效率试验结果有很大跌落，而单级性能的下降体现在第2级。第1级压比和效率计算值较试验值均偏小。双激波模型第1级压比和效率计算结果较正激波模型的略低。正激波模型总压比计算值比试验值约高1.63%，总效率计算值比试验值约高14.18%。而双激波模型总压比计算值跟试验值很吻合，总效率计算值比试验值约高7.28%。双激波模型总压比和总效率计算结果更接近试验值。

近堵塞点各级转、静子损失试验值和计算值沿展向分布如图9、10所示。

图9 第1级损失试验值与计算值

图10 第2级损失试验值与计算值

从图9中可见，第1级转、静子损失试验值沿展向变化趋势与近设计点趋势比较接近。第1级转子尖部2种模型损失计算值很接近，而根部双激波模型转子损失计算值较试验值偏大，正激波模型转子损失计算值跟试验值更接近。第1级静子损失计算值跟试验值比较接近。从图10中可见，第2级转子损失试验值在叶尖、叶中和叶根局部有跌落，静子叶根损失试验值有提高很大，叶尖损失试验值稍有增大。第2级转子损失计算值沿展向变化不大，各展向位置双激波模型计算值比正激波大约0.05，更接近试验值。第2级静子损失计算值相比试验值有很大差异。

各级绝热效率试验值和计算值沿展向分布如图11、12所示。

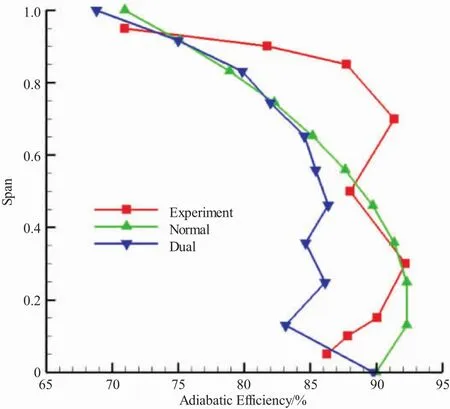
图11 第1级绝热效率试验值与计算值

从图11中可见，第1级绝热效率试验值与近设计点试验值比较接近。第1级叶尖处两种模型效率计算结果基本一致，正激波模型在叶根部分效率计算值与试验值很接近，双激波模型由于叶根部分有较大的损失计算值，叶根效率计算值相对较低。从图12中可见，第2级效率试验值沿展向变化较曲折，且在叶根处很低。第2级效率计算值比试验值高很多，沿展向变化较平滑。双激波模型计算值比正激波模型低5%左右，更接近试验结果。

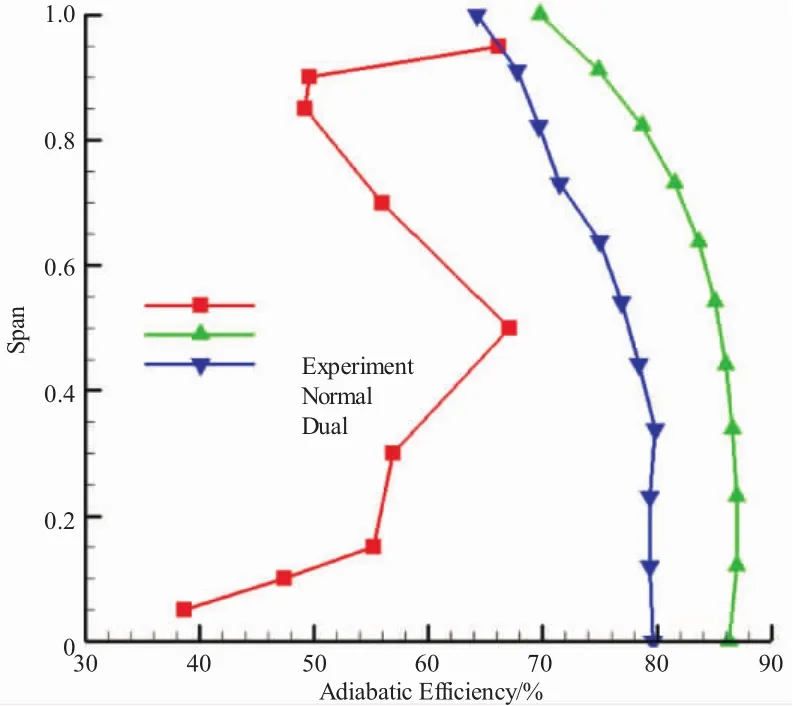
图12 第2级绝热效率试验值与计算值

各级转子出口相对气流角和静子出口气流角试验值和计算值沿展向分布如图13、14所示。

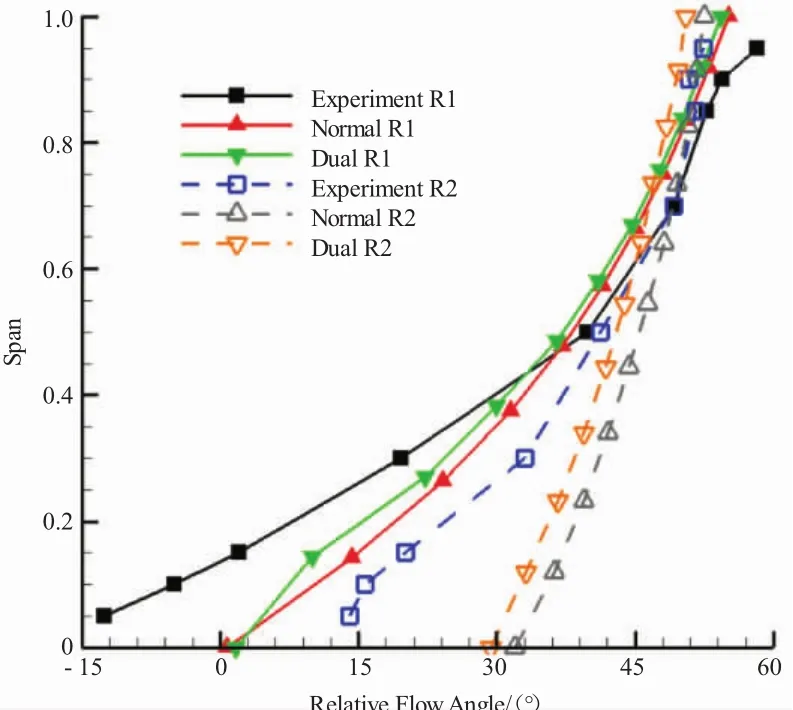
图13 转子出口相对气流角试验值与计算值

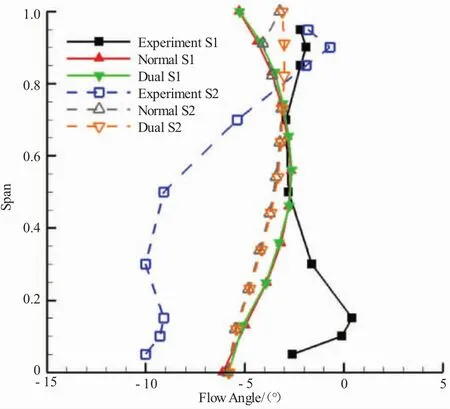
图14 静子出口气流角试验值与计算值

从图13中可见，第2级转子出口相对气流角试验值与近设计点试验值很接近。计算值比较接近试验值，在叶根部分比试验值偏大。从图14中可见，第1级静子出口气流角试验值沿展向变化趋势与近设计点趋势仍比较接近，第2级静子出口气流角试验值在叶尖处接近0°，而在叶中到叶根部分基本为-10°。第1级静子叶展中部出口气流角计算值跟试验值很贴近，在叶尖和叶根处差别较大。第2级静子出口气流角计算结果基本比试验结果大。

综合来看，利用双激波模型计算近堵塞工况，损失计算结果比正激波模型的大，总压比和总效率结果更接近试验值。

4.4 全工况特性计算

分别对95%、100%、110%设计转速下工况进行了计算，得到了特性曲线，并与试验曲线进行了比较，如图15、16所示。

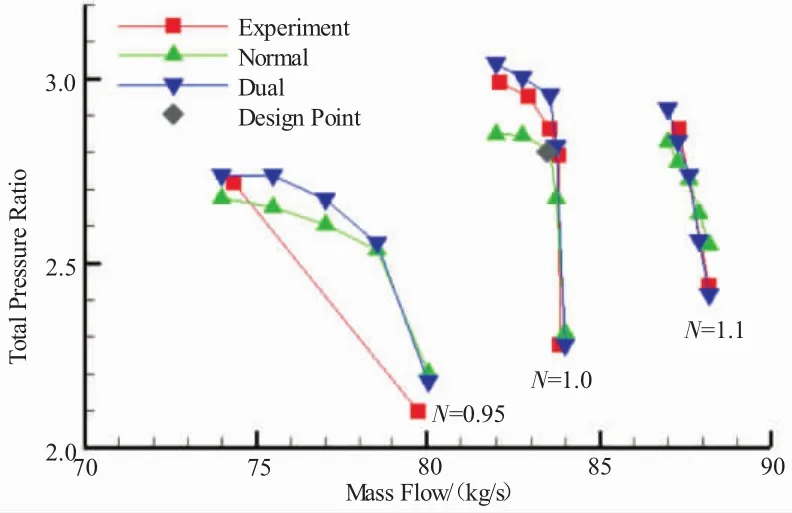
图15 增压比全工况特性试验值与计算值

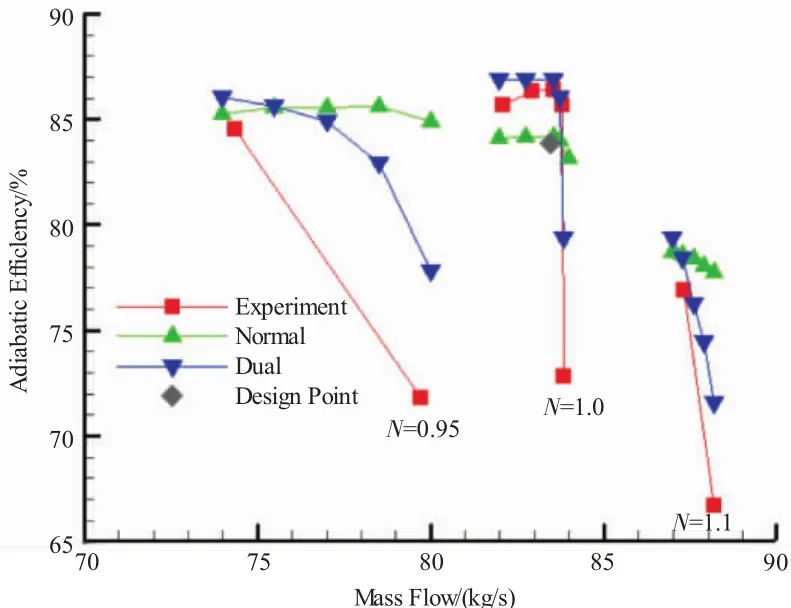
图16 绝热效率全工况特性试验值与计算值

从图15中可见，在等转速下较低流量下，双激波模型压比计算值比正激波模型高。在95%、100%设计转速线近堵塞点处2种模型计算值很接近，但110%设计转速线近堵塞点处双激波模型计算值与试验值吻合更好。双激波模型100%设计转速线更接近试验曲线。从图16中可见，双激波模型等转速效率计算值随流量变换更陡峭，而正激波模型计算值变化比较平缓。各转速线近堵塞点处，双激波模型计算值有较大跌落，比较符合试验结果，而正激波模型计算值下降不大。双激波模型100%设计转速线也更接近试验曲线。

综合来看，双激波模型的各转速特性线更接近试验结果，尤其在绝热效率特性图上，正激波模型效率计算值随流量变化不够明显，而双激波模型效率变化趋势跟试验值符合较好。

5 结论

本文利用流线曲率法结合正激波和改进的双激波模型对某型2级风扇进行了数值模拟，得到了近设计点、近堵塞点和全工况的特性，结论如下：

（1）本文发展的性能预估方法能有效计算跨声速轴流风扇/压气机性能和气动参数沿展向分布的规律，对设计点特性计算精度较高。

（2）不同激波模型对激波损失预估有较大差异，损失计算值会影响到增压比和绝热效率的预估，尤其是绝热效率受损失计算结果影响很大。

（3）对于跨声速风扇/压气机，在近设计点激波损失预估和特性计算上，正激波模型基本满足工程需求。而改进的双激波模型在非设计点损失预估和特性计算上结果更准确。

要更准确地计算非设计点的损失和特性参数，还需要研究更有效的二次流损失和叶型损失模型，需要在今后工作中进一步完善。

[1]胡江峰,竺晓程,杜朝辉.一种跨声速轴流压气机性能预测的数值方法[J].航空动力学报,2011,26（1）:122-127.HU Jiangfeng,ZHU Xiaocheng,DU Zhaohui.Numerical method of transonic axial compressor performance prediction [J].Journal of Aerospace Power,2011,26（1）:122-127.（in Chinese）

[2]刘波,马乃行,杨小东,等.适应较大叶型弯角范围的轴流压气机落后角模型[J].航空动力学报,2014,29（8）:1824-1831.LIU Bo,MA Naixing,YANG Xiaodong,et al.Deviation angle models suitable for wider range of blade profile camber in axial-flow compressor[J].Journal of Aerospace Power,2014,29（8）:1824-1831.（in Chinese）

[3]祝启鹏,高丽敏,李瑞宇,等.跨声速多级轴流压气机特性预估及分析[J].推进技术,2014,35（10）:1342-1348.ZHU Qipeng,GAO Limin,LI Ruiyu,et al.Performance prediction and analysis of multi-stage transonic axial compressors[J].Journal of Propulsion Technology,2014,35（10）:1342-1348.（in Chinese）

[4]Novak R A.Streamline Curvature Computing Procedure for Fluid-Flow Problems[J].ASME Journal of Engineering for Power,1967,89（4）:478-490.

[5]袁宁,张振家,顾中华,等.涡喷发动机压气机三种S2流面计算程序的比较[J].推进技术,1998,19（1）:50-56.YUAN Ning,ZHANG Zhenjia,GU Zhonghua,et al.A comparison of three kinds of calculation program of S2 stream surface in the compressor of aero-engine[J].Journal of Propulsion Technology，1998,19（1）:50-56.（in Chinese）

[6]Miller G R,Lewis G W,Hartmann M J.Shock losses in transonic compressor blade rows[J].ASME Journal of Engineering for Power,1961,83（2）:235-242.

[7]赵勇,胡骏,郑大勇.用双激波模型计算风扇/压气机非设计点的性能[J].南京航空航天大学学报,2006,38（5）:545-550.ZHAO Yong,HU Jun,ZHENG Dayong.Dual-shock loss model for off-design performance calculation of fan/compressor[J].Journal of Nanjing University of Aeronautics&Astronautics,2006,38（5）:545-550.（in Chinese）

[8]LI Bo,GU Chunwei,LI Xiaotang,et al.Development and application of a through flow method for high-loaded axial flow compressors[J].Science China Technology Sciences,2016,59（1）:93-108.

[9]Bloch G S.Flow Losses in supersonic compressor cascades[D].Virginia:Virginia Polytechnic Institute and State University,1996.

[10]Boyer K M.An Improved streamline curvature approach for off-design analysis of transonic compression systems[D].Virginia:Virginia Polytechnic Institute and State University,2001.

[11]Biollo R,Benini E.Recent advances in transonic axial compressor aerodynamics[J].Progress in Aerospace Science,2013,56:1-18.

[12]闫转运,成金鑫,陈江.多级轴流压气机通流造型一体化设计研究[J].工程热物理学报,2016,37（6）:1218-1224.YAN Zhuanyun, CHENG Jinxin, CHEN Jiang. Integrated through-flow and blade shape design of multi-stage axial flow compressor[J].Journal of Engineering Thermophysics,2016,37（6）:1218-1224.（in Chinese）

[13]Messenger H E,Kennedy E E.Two-stage fan I.aerodynamic and mechanical design[R].NASA-CR-120859.

[14]Ruggeri R S,Benser W A.Performance of a highly loaded two-stage axial-flow fan[R].NASA-TM-X-3076.

[15]Johnsen I A,Bullock R O.Aerodynamic design of axial-flow compressors[R].NASA-SP-36.

[16]Herrig L J,Emery J C,Erwin J R.Systematic two-dimensional cascade tests of NACA 65-Series compressors[R].NACA-RM-L51G31.

[17]邓熙,刘波,马乃行.高亚声速大弯角轴流压气机平面叶栅损失模型研究[J].推进技术,2015,36（9）:1302-1308.DENG Xi,LIU Bo,MA Naixing.Investigation of loss model applicable to large range of high subsonic cascade in axial-flow compressor[J].Journal of Propulsion Technology,2015,36（9）:1303-1308.（in Chinese）

[18]杜文海,吴虎,阮建刚.跨声速轴流压气机特性计算用激波损失模型[J].推进技术,2007,28（4）:378-382.DU Wenhai,WU Hu,RUAN Jiangang.A shock loss model for the transonic axial compressor[J].Journal of Propulsion Technology,2007,28（4）:378-382.（in Chinese）

[19]König W M,Hennecke D K,Fottner L.Improved Blade Profile loss and deviation angle models for advanced transonic compressor bladings:Part II-A model for supersonic flow[J].ASME Journal of Turbomachinery,1996,117（1）:81-87.

[20]Klapproth J F.Approximate relative-total-pressure Losses of an Infinite cascade of supersonic blades with finite leading-edge thickness[R].NACA-RM-E9L21.

Study on Performance Simulation and Shock Model for Axial-Flow Compressor

JIANG Zhu-yu1,FAN Zhao-lin1,LIU Bo2
（1.China Aerodynamics Research and Development Center,Mianyang Sichuan 621000,China;2.School of Power and Energy,Northwestern Polytechnical University,Xi'an 710072,China）

In order to quickly and accurately predict performance and shock loss for axial-compressor,based on axial-flow compressor S2 flow surface streamline curvature method,simulation of the performance of a two-stage transonic fan was performed involving normal shock model and improved dual-shock model.Thus the overall performance and aerodynamic parameters on near-design and near-choke point,separately at 100%and 99.76%design rotation speed,and characteristic curves at 95%,110%,and 110%design speed were obtained.The differences in prediction of shock loss and calculation of fan/compressor performance between the two shock loss models have been analyzed by comparing the simulation results and experiment data.The results show that on the near-design point,with the normal shock model,calculation result of radial distribution of loss is close to test result,and results of total pressure ratio and total efficiency are proximately lower than test result by 1.96%and 2.54%separately.Thus,the normal shock model can satisfy engineering need.While on the near-choke point,with improved dual-shock shock model,calculation result of total loss is closer to test result,result of total pressure ratio is consistent with test result,and result of total efficiency is about 7.28%higher than test result.And calculated characteristic curves are more similar to test curves.Therefore the use of improved dual-shock loss model can provide a more accurate calculation of shock loss and performance parameters on far off-design point.

axial-flow compressor;streamline curvature calculation;shock model;loss prediction;performance simulation

V 231.3

A

1 0.1 3477/j.cnki.aeroengine.201 7.02.01 4

2016-11-10 基金项目：国家自然科学基金（51676162）资助

蒋筑宇（1991），男，在读硕士研究生，研究方向为叶轮机气动热力学；E-mail：kongjianglieren@163.com。

蒋筑宇，范召林，刘波.轴流压气机特性计算及激波模型研究[J].航空发动机，2017，43（2）：48-55.JIANG Zhuyu,FAN Zhaolin,LIU Bo.Study on performance simulation and shock mdelforaxial-flow compressor[J].Aeroengine，2017，43（2）：48-55.

（编辑：李华文）