基于半解析自洽理论研究相对论激光脉冲驱动下阿秒X射线源的产生∗

王少义 谭放 吴玉迟2)3) 范全平 矫金龙 董克攻 钱凤曹磊峰2)3) 谷渝秋2)3)

1)(中国工程物理研究院,激光聚变研究中心,绵阳 621900)

2)(中国工程物理研究院,等离子体重点实验室,绵阳 621900)

3)(上海交通大学,协同创新中心,上海 200240)

基于半解析自洽理论研究相对论激光脉冲驱动下阿秒X射线源的产生∗

王少义1)谭放1)吴玉迟1)2)3)†范全平1)矫金龙1)董克攻1)钱凤1)曹磊峰1)2)3) 谷渝秋1)2)3)

1)(中国工程物理研究院,激光聚变研究中心,绵阳 621900)

2)(中国工程物理研究院,等离子体重点实验室,绵阳 621900)

3)(上海交通大学,协同创新中心,上海 200240)

自洽振荡镜模型,高次谐波,单阿秒脉冲

发展了一种描述相对论激光脉冲与稠密等离子体相互作用产生阿秒X射线源的半解析自洽理论.该理论模型不仅可以获得等离子体界面的振荡轨迹、振荡面电场和磁场等物理参数,而且能够精确计算出激光脉冲驱动下阿秒X射线源的频谱,结果与粒子模拟程序一致.理论计算结果表明阿秒X射线源的辐射特性与等离子体界面随时演化过程相关,在周期量级激光场驱动下等离子体界面振荡振幅呈现中心不对称,通过改变激光场的载波包络相位实现对等离子体界面振荡的控制,获得准单阿秒X射线源.

1 引 言

超短超强激光技术的飞速发展为研究光与物质相互作用提供了有力工具,新物理新现象陆续被发现,比如电离、解离、高次谐波、粒子加速[1−8]等,其中高次谐波是突破飞秒极限实现阿秒脉冲光源的首选方案.利用激光驱动惰性气体产生高次谐波获得阿秒X射线辐射源的方案最早被提出,同时也得到了最广泛的理论和实验研究[9−17].在此方案中,当激光场作用在原子、分子时,前半个周期原子库仑势垒被正向激光场压低,原子(离子)外层电子发生隧穿电离;电离以后的电子在激光场中运动,并被加速得到能量;后半周期,当激光场反向时,电子反向运动和母离子复合.在复合过程中,电子把动能转换成光子能量,并辐射出高次谐波,其能量等于电子返回时动能与电离能之和[18,19].高次谐波辐射过程在每个激光周期发生两次,获得一串阿秒脉冲序列.目前为止,实验上得到的最短单阿秒脉冲周期是67 as[20],虽然激光驱动惰性气体产生阿秒X射线源的物理机制被实验广泛证实,但是此方案中为了使气体不发生过度电离影响谐波产生,入射激光强度不能太高(＜1016W/cm2),导致获得的阿秒X射线源强度很弱,因此无法用于探测一些复杂的非线性物理过程如单分子成像等,其应用范围极大地受到限制.

固体靶由于其高密度可以承受更大的电荷分离场,使得大量电子可以在激光场下振荡达到更高的能量密度和电流密度,从而能够产生比气体靶更高阶以及更强的高次谐波[21−25].2007年1月法国萨克莱研究中心的Quéré[26]提出用弱相对论激光(a0∼1)照射固体靶驱动相干尾场辐射可以产生更高次谐波.但由于这种机制产生的谐波次数与亮度受限于靶最大等离子体密度以及激光强度,因此得到的阿秒辐射脉冲强度和光子能量仍不足以达到实际应用需要的条件.此外,人们发现当激光峰值功率达到相对论强度时,在有质动力作用下固体靶表面趋肤深度内电子层相对论速度振荡对入射激光产生多普勒频移现象[27,28](振荡镜模型).早期实验和粒子模拟程序(PIC)工作证明了振荡镜机制能够产生更短波长、更高亮度的高次谐波,引起国际上广泛的研究[21−25,27,28].

振荡镜机制下高次谐波的理论研究主要基于PIC程序,为了计算更高次数的谐波谱,需要网格密度小于千分之波长,这极大地增加了计算所需时间和资源.为了更加直观地计算高次谐波谱,Bulanov和Naumova[29]以及Baeva等[30]提出了一种简单的振荡镜模型,给出了一个解析公式,获得各阶高次谐波强度与次数的关系,但简单的解析公式无法获得高次谐波谱产生的物理过程.李昆等[28]和Liu等[31]分别基于弱相对论强度下得到了高次谐波谱的解析表达式,并获得了激光强度、等离子体密度等物理参数对高次谐波谱的影响,但无法描述强相对论强度下的谐波谱.近两年,由西班牙科学家Debayle等[32−34]基于流体近似模型发展了一种精确描述等离子体界面运动轨迹的自洽模型,从而可获得精确的高次谐波谱.在他们的工作中采用平面波近似,虽然获得了平面波驱动下高次谐波产生的物理过程,但不能回答激光脉宽以及载波包络相位等物理参量是否对高次谐波产生的物理过程存在影响.实验室条件下激光存在脉宽,需要进一步发展这种模型,才能准确指导高次谐波实验研究.

本文在Debayle等提出的等离子体界面振荡模型的基础上,发展了一种能够在任意激光脉宽和载波包络相位情况下高次谐波产生的自洽振荡模型.该模型不仅可以获得相对论激光场与稠密等离子体相互作用过程中等离子体界面的振荡轨迹、振荡面电场和磁场等物理参数,还能够精确地计算出不同脉宽激光场驱动下高次谐波的频谱.结果表明,利用周期量级激光场可有效减少等离子体界面的振荡次数,通过改变激光场载波包络相位实现对等离子体界面振荡的控制,从而影响高次谐波谱辐射,获得准单阿秒脉冲.

2 模型和参数

该模型从电子相对论运动方程、连续性方程、麦克斯韦-安培方程以及泊松方程出发,并假设激光的焦斑远大于激光波长、等离子体密度足够大,忽略离子的运动和碰撞,在本文中各物理量采用归一化量纲,矢势、等离子体密度、空间和时间坐标分别用和1/ω0归一化,其方程组如下:

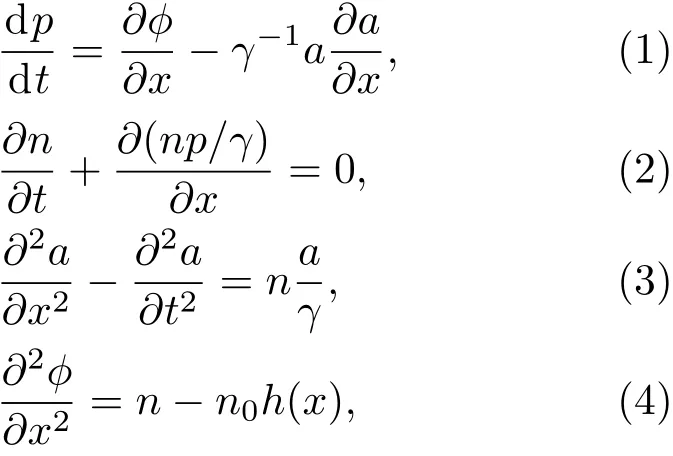
其中p,a,n,ϕ分别为电子动量、激光矢势、电子密度和静电势.由于高次谐波的辐射与等离子体界面的振荡有关,需要从上述方程组获得等离子体界面的运动方程.令λs(t),as(t)=a(λs,t)和bzs(t)=∂xa(λs,t)分别表示等离子体界面的位置、电场以及磁场.从方程(1)出发,可以获得等离子体界面的运动方程:

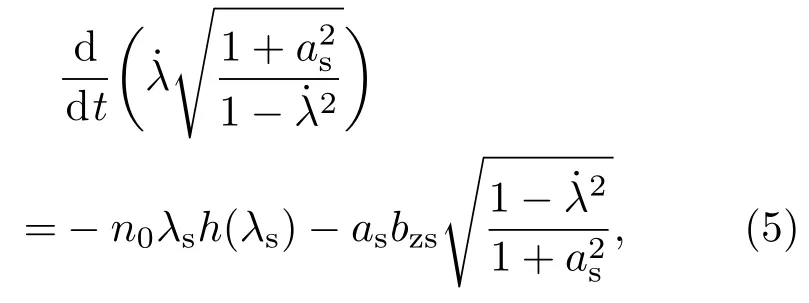
其中,h(x)为阶梯函数.根据电场和磁场的连续边界条件可得:

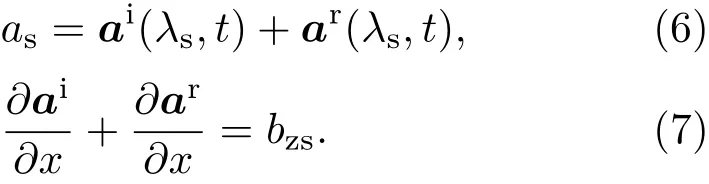
在上式中,ai为入射激光波矢,ar为反射光的波矢.其中,激光波矢表示为

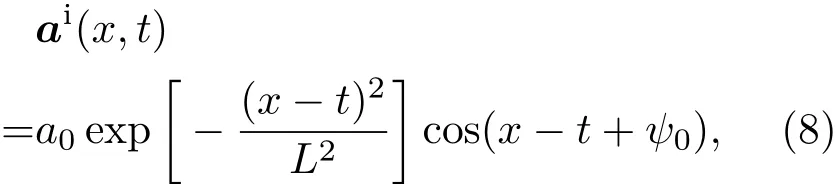
其中a0为归一化振幅,L为激光脉冲脉宽,ψ0为激光场的载波相位.由反射光的波矢可以写成λs+t的函数,则可以得到∂xar=∂tar,并将方程(8)代入到(6)和(7)式中,可得

由(1)和(4)式,对于稠密等离子体,可以得到等离子体界面处电场as和bzs的关系.

对于λs≥0的情况,

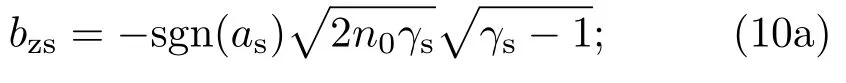
对于λs＜0的情况,

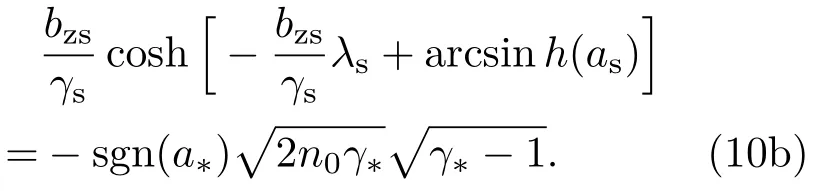
其中,

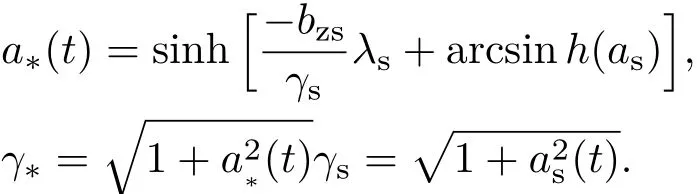
联合求解常微分方程组(5),(9)和(10)式,便能够获得等离子体界面的运动轨迹.

由(6)式可得

(11)式中对反射光的电场进行傅里叶变换,便可得到高次谐波谱.

为了验证半解析自洽模型的正确性,采用一维LPIC++程序对高次谐波谱进行计算.假设激光脉冲正入射到稠密等离子体上,a0=20,激光从左向右传播.稠密等离子体的厚度为2λ0(λ0为激光波长),密度为90nc(nc为等离子体临界密度在模拟中,每个激光波长内设置1000个空间网格,每个网格内电子数为900.在模拟中只考虑电子的运动,空间坐标X轴从0λ0到15λ0,激光入射从左到右,稠密等离子体位于坐标为6λ0到8λ0处.

3 结果与讨论

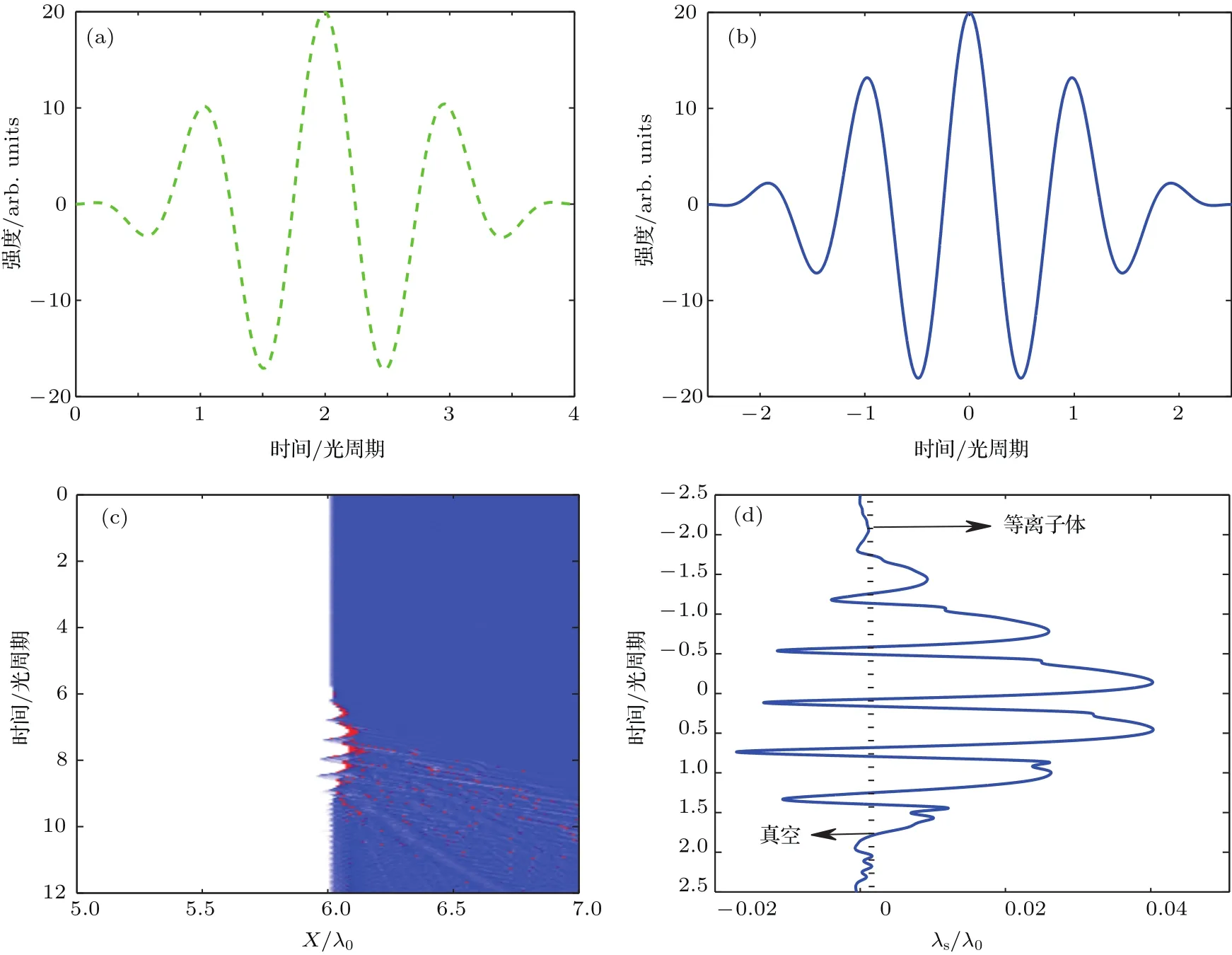
图1 (网刊彩色)(a),(c)为PIC模拟和半解析自洽模型采用的激光场;(b),(d)分别为PIC模拟和半解析自洽模型得到的等离子体界面随时间演化过程Fig.1.(color online)The electric fi eld for the PIC(a)and the semi-analytical self-consistent model(c);the electronic distribution obtained by PIC(b)and the semi-analytical self-consistent model(d).

为了给出超强激光场与等离子体相互作用的物理过程,图1(b)给出了利用PIC程序模拟周期量级激光场驱动下等离子体界面随时间的演化过程.模拟中采用的激光场如图1(a)所示,全宽为三个光周期.从图1(b)可以清晰地看到等离子体界面随时间呈现周期振荡结构,这些振荡结构是由激光电场的振荡引起的,每个光周期等离子体界面振荡两次,振荡的幅度与对应的激光电场峰值有关.根据振荡镜机制,入射激光在高速振荡等离子体界面产生多普勒效应,因此高次谐波的辐射依赖等离子体界面的振荡情况.利用一维LPIC++程序模拟等离子体密度随时间演化过程,这些图像能够给出等离子体界面的振荡情况.利用同样的激光场,如图1(c)所示,采用相同的等离子体密度.设x=0为等离子体与真空的分界线,x＜0为真空,x≥0为等离子体区域,如图1(d)中黑色虚线所示.图1(d)中实线为半解析自洽模型计算获得的等离子体界面位置λs(t)随时间的演化过程,从图中可以明显看出存在6次振荡,等离子体界面随时间演化过程与PIC模拟得到的结果非常的符合.经过与PIC模拟结果对比,半解析自洽模型能够准确获得等离子体界面随时间演化的物理过程.

图2 (网刊彩色)在相同模拟参数下,PIC程序(红色)以及自洽模型(绿色)计算获得的高次谐波谱Fig.2.(color online)High-order harmonic spectrum obtained by the PIC(red curve)and self-consistent model(green curve)in the same parameters.

图3 (网刊彩色)不同脉宽下等离子体界面随时间演化以及对应的等离子体界面处的电场(红色曲线)和磁场(绿色曲线)(a),(d)平面波;(b),(e)10个光周期;(c),(f)3个光周期Fig.3.(color online)The λs(t)vs.time with different durations of laser and the corresponding electric fi eld(red curve)and magnetic fi eld(green curve):(a),(d)plane wave;(b),(e)ten optical cycles;(c),(f)three optical cycles.

通过等离子体界面振荡演化可以直接获得高次谐波谱,图2中绿色实线给出了利用自洽模型获得的谐波频谱图,可以看出,低次部分谐波强度较强,随着谐波次数增加,强度迅速下降,非常符合振荡镜模型获得的高次谐波频谱结构.为了进一步对比,在相同参数条件下利用PIC程序计算获得高次谐波谱如图2中红色实线所示.通过对比发现,两种方法计算获得的谐波频谱整体趋势一致,但在低次部分(小于10次),有些细节表现有些差异,在高次部分的谐波调制等细节,两种方式计算的结果非常符合.从图2可以看出半解析自洽模型能够准确计算出周期量级激光场驱动下产生高次谐波谱.

为了进一步获得不同激光脉宽下高次谐波产生的物理过程,图3(a)—(c)分别给出了平面波、10个光周期以及3个光周期激光脉冲驱动下等离子体界面的演化过程.从图中可以看出,在平面波驱动下,等离子体界面振荡呈现出非常规则的周期性;由于等离子体的振荡是由激光电场振荡引起的,当驱动场为脉冲激光场时,等离子体界面振荡振幅的演化呈现类似的时间包络,并且为中心对称结构.当驱动激光场为周期量级时,等离子体界面随时间演化也是周期量级,并呈现中心不对称性,这是由于激光场的载波包络相位的影响.等离子体界面处的电场和磁场在图3(d)—(f)所示,所有曲线随时间演化的趋势与等离子体界面演化趋势一致,磁场在每半个光周期都存在一个跳变点,这是由于等离子体经过背景离子界面时产生的.从(11)式可以得出,高次谐波的辐射是由等离子体界面处对磁场的傅里叶变换得到的,因此磁场随时间演化与谐波谱直接相关.对比图3,采用周期量级的驱动激光场,可以有效减少等离子体界面振荡次数,从而影响高次谐波辐射.

图4 (网刊彩色)不同载波相位下等离子体界面随时演化(a)—(c)以及对应的高次谐波谱(d)Fig.4.(color online)The λs(t)vs.time with different phases of laser(a)–(c),and the corresponding harmonic spectrums(d).

为了研究激光载波包络相位对等离子体界面运动轨迹的影响,将激光脉宽短至接近两个光周期,如图4所示.当激光载波包络相位为0π时,存在三次振荡,中间一次振荡振幅最强,两边振荡振幅小一些,如图4(a)所示;当载波包络相位为0.25π时,两侧对应的振荡振幅减弱,如图4(b)所示;当载波相位为0.5π时,中间时刻对应的等离子体界面振荡振幅已经明显大于相邻的振荡振幅.图4(d)给出了三种不同载波包络相位下高次谐波谱,可以看出蓝色曲线在高次部分的调制大于其他两条曲线,这是由于在载波相位为0π时,等离子体界面主要存在三次振荡,每次振荡会辐射一次高次谐波,三次不同时空辐射的谐波相干叠加,导致高次谐波谱的调制结构.为了进一步说明不同载波包络相位下等离子体界面振荡对高次谐波辐射的影响,图5给出了不同载波包络相位下高次谐波的时频分析图,模拟参数与图4(a)和图4(c)一致.采用切比雪夫窗口,获得的时频分析图能够定性地说明不同时刻高次谐波辐射情况.从图5(a)可以看出存在4个清晰的条纹,这意味着高次谐波主要是由这四个时刻辐射的.对比4个条纹的强度,可以发现T0时刻辐射对高次谐波的贡献比T1和T2时刻的贡献要略大一些.该T0时刻对应的等离子体界面振荡幅度比相邻时刻等离子体振荡幅度要大一些(见图4(a)中第0—0.5光周期),该时刻对高次谐波的产生贡献最大,但相邻时刻的贡献不能忽略.当激光场载波包络相位为0.5π,从图5(b)中高次谐波时频分析可以看出,P0时刻的条纹强度明显高于P1和P2时刻,这意味着P0时刻等离子体界面的振荡对高次谐波产生起主要贡献,对应时刻等离子体界面振荡振幅也比相邻时刻的振幅要高,如图4(c)所示.综上所述,通过改变驱动激光场的载波包络相位,有效控制等离子体界面的振荡情况,从而影响高次谐波的辐射.

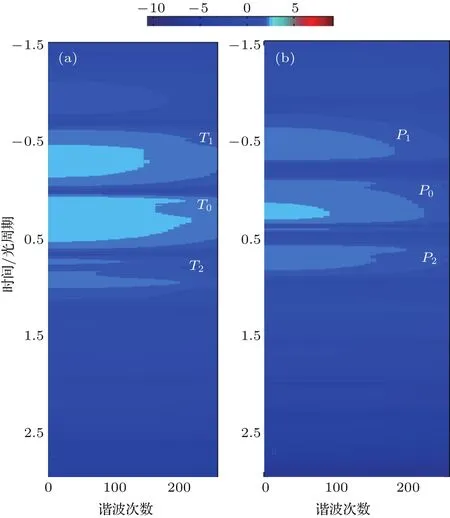
图5 (网刊彩色)载波包络相位分别为0π(a)和0.5π(b)时高次谐波的时频分析图Fig.5.(color online)Time-frequency analysis of the high-order harmonics driven by the few-cycle fi eld with different carrier envelope phases of 0π(a)and 0.5π(b).

图6 (网刊彩色)不同载波包络相位下利用50—100次谐波的叠加获得的阿秒脉冲Fig.6.(color online)Attosecond pulses by fi ltering harmonics from 50th to 100th with different carrier-envelope phases.

将获得的第50—100次谐波过滤,补偿啁啾,得到了接近40 as的阿秒脉冲如图6所示.图6(a)为激光载波包络相位为0π时获得的阿秒脉冲,从图中可以看出主脉冲两侧存在两个卫星脉冲.当激光载波包络相位为0.25π和0.50π时,两个卫星脉冲强度得到极大的减弱,与主脉冲相比可以忽略不计.从图6可以发现,阿秒脉冲的卫星脉冲与等离子体界面振荡次数和振荡振幅相关,通过改变激光场的载波包络相位,控制等离子体界面的振荡,从而获得准单阿秒脉冲.

4 结 论

研究了相对论激光脉冲与稠密等离子体相互作用的物理过程.发展了基于冷流体近似的半解析自洽模型,该模型不仅可以给出激光脉冲驱动下等离子体界面的振荡轨迹、振荡面电场和磁场等物理参数,还能够精确地计算出不同脉宽激光场驱动下高次谐波的频谱,计算结果与PIC程序模拟结果一致.通过该模型计算表明等离子体界面振荡次数依赖于驱动激光脉宽,在周期量级激光场驱动下,等离子体振荡轨迹呈现中心不对称性,这种不对称性与激光的载波包络相位有关.通过改变周期激光场的载波包络相位实现对等离子体界面运动情况的控制,从而影响高次谐波谱辐射,获得准单阿秒脉冲.

[1]Bartels R A,Paul A,Green H,Kapteyn H C,Murnane M M,Backus S,Christov I P,Liu Y,Attwood D,Jacobsen C 2002Science297 376

[2]Rundquist A,Durfee III C G,Chang Z,Herne C,Backus S,Murnane M M,Kapteyn H C 1998Science280 1412

[3]Kling M F,Siedschlag C,Verhoef A J,Khan J I,Schultze M,Uphues Th,Ni Y,Uiberacker M,Drescher M,Krausz F,Vrakking M J J 2006Science312 246

[4]Zhou Y M,Huang C,Liao Q,Lu P X 2012Phys.Rev.Lett.107 053004

[5]Qiao B,Zepf M,Borghesi M,Geissler M 2009Phys.Rev.Lett.102 145002

[6]Faure J,Glinec Y,Pukhov A,et al.2004Nature431 541

[7]Chen L M,Liu F,Wang M,et al.2010Phys.Rev.Lett.104 215004

[8]Hentschel M,Kienberger R,Spielmann C,Reider G A,Milosevic N,Brabec T,Corkum P,Heinzmann U,Drescher M,Krausz F 2001Nature414 509

[9]Pfeifer T,Gallmann L,Abel M J,Nagel P M,Neumark D M,Leone S R 2006Phys.Rev.Lett.97 163901

[10]Lan P,Lu P,Cao W,Wang X 2007Phys.Rev.A76 043808

[11]Christov I P,Murnane M M,Kapteyn H C 1997Phys.Rev.Lett.78 1251

[12]Wang S,Hong W,Lan P,Zhang Q,Lu P 2009J.Phys.B42 105601

[13]Zhang Q,Lu P,Lan P,Hong W,Yang Z 2008Opt.Express16 9795

[14]Zeng Z,Zheng Y,Cheng Y,Li R,Xu Z 2012J.Phys.B45 074004

[15]Zhang Q,He L,Lan P,Lu P 2014Opt.Express22 13213

[16]Wei P,Miao J,Zeng Z,Li C,Ge X,Li R,Xu Z 2013Phys.Rev.Lett.110 233903

[17]Zhong H Y,Guo J,Zhang H D,Du H,Liu H X 2015Chin.Phys.B24 073202

[18]Lewenstein M,Balcou P,Ivanov M Yu,L’Huillier A,Corkum P B 1994Phys.Rev.A49 2117

[19]Corkum P B 1993Phys.Rev.Lett.71 1994

[20]Zhao K,Zhang Q,Chini M,et al.2012Opt.Lett.37 3891

[21]Dromey B,Zepf M,Gopal A,Lancaster K,Wel M S,Krushelnick K,Tatarakis M,Vakakis,Moustaizis S,Kodama R,Tampo M,Stoeckl C,Clarke R,Habara H,Neely D,Karsch S,Norreys P 2006Nat.Phys.2 456

[22]Ndabashimiye G,Ghimire S,Wu M,Browne D A,Schafer K J,Gaarde M B,Reis D A 2016Nature534 520

[23]Pan K Q,Zheng C Y,He X T 2016Phys.Plasma23 023109

[24]Bai Y L,Zhang Q J,Tian M,Cui C H 2013Acta Phys.Sin.62 125206(in Chinese)[白易灵,张秋菊,田密,崔春红2013物理学报62 125206]

[25]Zhang X M,Shen B F,Shi Y,Wang X F,Zhang L,Wang W P,Xu J C,Yi L Q,Xu Z Z 2015Phys.Rev.Lett.14 173901

[26]Quéré F,Thaury C,Monot P,Dobosz S,Martin P,Geindre J P,Audebert P 2006Phys.Rev.Lett.96 125004

[27]Zhang Q J,Sheng Z M,Zhang J 2003Acta Phys.Sin.53 2180(in Chinese)[张秋菊,盛政明,张杰 2003物理学报53 2180]

[28]Li K,Zhang J,Yu W 2003Acta Phys.Sin.52 1412(in Chinese)[李昆,张杰,余玮2003物理学报52 1412]

[29]Bulanov S V,Naumova N M,Pegoraro F 1994Phys.Plasmas1 745

[30]Baeva T,Gordienko S,Robinson A P L,Norreys P A 2011Phys.Plasma18 056702

[31]Liu J S,Xia C,Liu L,Li R X,Xu Z Z 2009Laser Particale Beams27 365

[32]Sanz J,Debale A,Mima K 2012Phys.Rev.E85 046411

[33]Debale A,Sanz J,Gremillet L,Mima K 2013Phys.Plasmas20 053107

[34]Debayle A,Sanz J,Gremiller L 2015Phys.Rev.E92 053108

Attosecond X-ray generation driven by the relativistic laser pulse based on the semi-analytical self-consistent theory∗

Wang Shao-Yi1)Tan Fang1)Wu Yu-Chi1)2)3)†Fan Quan-Ping1)Jiao Jin-Long1)Dong Ke-Gong1)Qian Feng1)Cao Lei-Feng1)2)3)Gu Yu-Qiu1)2)3)

1)(Research Center of Laser Fusion,China Academy of Engineering Physics,Mianyang 621900,China)
2)(Key Laboratory of Sciences and Technology on Plasma Physics,China Academy of Engineering Physics,Mianyang 621900,China)
3)(IFSA Collaborative Innovation Center,Shanghai Jiao Tong University,Shanghai 200240,China)

18 April 2017;revised manuscript

1 June 2017)

A semi-analytical theory of the interaction between a relativistic laser pulse and the overdense plasma to generate an attosecond X-ray source is presented.The physical parameters such as plasma oscillation trajectory,surface electric fi eld and magnetic fi eld can be given by this model,and the high-order harmonic spectrum is also calculated accurately from the solution of the plasma surface oscillations,the obtained result is consistent with the result from the PIC simulation program.This model can be valid for arbitrary laser duration,solid densities,and a large set of laser peak intensities(1018–1021W/cm2).In addition,the model is not applicable for the small laser focal spots(less than ten times the laser wavelength),although two-dimensional e ff ects such as the pulse fi nite size may signi fi cantly change the movement progress of the electrons,the laser spot can be larger than ten times the laser wavelength under the general laboratory conditions.

In this model,the laser energy absorption is small,and the electron kinetic pressure is also small.Due to the radiation pressure of the laser pulse,the electrons are pushed into the solid,forming a very steep density pro fi le.As a result,the relevant forces makes the electrons ponderomotive and the longitudinal electric fi eld is caused by the strong electric charge separation e ff ect.This semi-analytical self-consistent theory can give us a reasonable physical description,and the momentum equation and the continuity equation of the electric and magnetic fi eld at the boundary allow us to determine the plasma surface oscillations.The spatiotemporal characteristics of the re fl ected magnetic and electric fi eld at the boundary can allow us to determine the emitting characteristics of the high order harmonic.

Our results show that the radiation of the attosecond X-ray source is dependent on the plasma surface oscillation.The plasma surface oscillates with a duration about twice the laser optical cycle,and the high-order harmonics also emit twice the laser optical cycle,thus an attosecond pulse train driven by the multi-cycle laser pulse can be formed.By using a few-cycle laser fi eld,the smooth high-order harmonics can be obtained,which leads to a single attosecond pulse with high signal-to-noise ratio.In a word,our calculation results show that the time evolution progress of plasma surface can be controlled by changing the carrier envelope phase of the few-cycle laser pulse,and then the radiation progress of the high-order harmonics can be in fl uenced as result of a single attosecond X-ray pulse.

self-consistent theory,high-order harmonic,single attosecond pulse

(2017年4月18日收到;2017年6月1日收到修改稿)

10.7498/aps.66.204205

∗国家重大科学仪器专项(批准号:2012YQ130125)、国家自然科学基金(批准号:11405159,11375161,11174259)、国家自然科学基金联合基金(批准号:U1630246)、中国工程物理研究院院长基金(批准号:2014-1-017)、中国工程物理研究院科技发展基金(批准号:2015B0401090)、重点实验室基金(批准号:9140C680302130C68242)和国家科技部重点研发计划(批准号:2016YFA0401100)资助的课题.

†通信作者.E-mail:wuyc@caep.cn

©2017中国物理学会Chinese Physical Society

http://wulixb.iphy.ac.cn

PACS:42.65.Ky,52.38.Ph,52.59.YeDOI:10.7498/aps.66.204205

*Project supported by the National Science Instruments Major Project of China(Grant No.2012YQ130125),the National Natural Science Foundation of China(Grant Nos.11405159,11375161,11174259),the Joint Funds of the National Natural Science Foundation of China(Grant No.U1630246),the President Foundation of China Academy of Engineering Physics(Grant No.2014-1-017),the Technology Development Foundation of China Academy of Engineering Physics(Grant No.2015B0401090),the Key Laboratory Foundation of the Sciences and Technology on Plasma Physics Laboratory,China(Grant No.9140C680302130C68242),and the National Key Research and Development Technology Project of China(Grant No.2016YFA0401100).

†Corresponding author.E-mail:wuyc@caep.cn